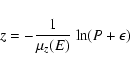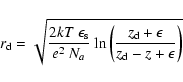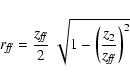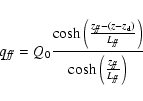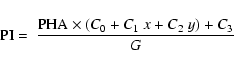| Issue |
A&A
Volume 494, Number 2, February I 2009
|
|
|---|---|---|
| Page(s) | 775 - 797 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361:200811157 | |
| Published online | 27 November 2008 | |
Modelling the spectral response of the Swift-XRT CCD camera: experience learnt from in-flight calibration
O. Godet1 - A. P. Beardmore1 - A. F. Abbey1 - J. P. Osborne1 - G. Cusumano2 - C. Pagani3 - M. Capalbi4 - M. Perri4 - K. L. Page1 - D. N. Burrows3 - S. Campana5 - J. E. Hill6,7 - J. A. Kennea3 - A. Moretti5
1 - X-ray and Observational Astronomy Group, Department of Physics & Astronomy, University of Leicester, LE1 7RH, UK
2 - INAF - Istituto di Astrofisica Spaziale e Fisica Cosmica Sezione di Palermo, via U. La Malfa 153, 90146 Palermo, Italy
3 - Department of Astronomy & Astrophysics, 525 Davey Lab, Pennsylvania State University, University Park, PA 16802, USA
4 - ASI Science Data Center, via G. Galilei, 00044 Frascati, Italy
5 - INAF - Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807, Merate (LC), Italy
6 - CRESST Goddard Space Flight Center, Greenbelt, Maryland 20771, USA
7 - Universities Space Research Association, 10211 Wincopin Circle, Suite 500, Columbia, MD 21044-3432, USA
Received 15 October 2008 / Accepted 21 November 2008
Abstract
Context. Since its launch in November 2004, Swift has revolutionised our understanding of gamma-ray bursts. The X-ray telescope (XRT), one of the three instruments on board Swift, has played a key role in providing essential positions, timing, and spectroscopy of more than 300 GRB afterglows to date. Although Swift was designed to observe GRB afterglows with power-law spectra, Swift is spending an increasing fraction of its time observing more traditional X-ray sources, which have more complex spectra.
Aims. The aim of this paper is a detailed description of the CCD response model used to compute the XRT RMFs (redistribution matrix files), the changes implemented to it based on measurements of celestial and on-board calibration sources, and current caveats in the RMFs for the spectral analysis of XRT data.
Methods. The RMFs are computed via Monte-Carlo simulations based on a physical model describing the interaction of photons within the silicon bulk of the CCD detector.
Results. We show that the XRT spectral response calibration was complicated by various energy offsets in photon counting (PC) and windowed timing (WT) modes related to the way the CCD is operated in orbit (variation in temperature during observations, contamination by optical light from the sunlit Earth and increase in charge transfer inefficiency). We describe how these effects can be corrected for in the ground processing software. We show that the low-energy response, the redistribution in spectra of absorbed sources, and the modelling of the line profile have been significantly improved since launch by introducing empirical corrections in our code when it was not possible to use a physical description. We note that the increase in CTI became noticeable in June 2006 (i.e. 14 months after launch), but the evidence of a more serious degradation in spectroscopic performance (line broadening and change in the low-energy response) due to large charge traps (i.e. faults in the Si crystal) became more significant after March 2007. We describe efforts to handle such changes in the spectral response. Finally, we show that the commanded increase in the substrate voltage from 0 to 6 V on 2007 August 30 reduced the dark current, enabling the collection of useful science data at higher CCD temperature (up to -50 ![]() C). We also briefly describe the plan to recalibrate the XRT response files at this new voltage.
C). We also briefly describe the plan to recalibrate the XRT response files at this new voltage.
Conclusions. We show that the XRT spectral response is described well by the public response files for line and continuum spectra in the 0.3-10 keV band in both PC and WT modes.
Key words: gamma rays: bursts - X-rays: general - instrumentation: detectors - methods: numerical
1 Introduction
Successfully launched on 2004 November 20, the Swift gamma-ray burst satellite (Gehrels et al. 2004) consists of three instruments: the wide-field of view, gamma-ray burst alert telescope (BAT; Barthelmy et al. 2005) and two narrow field instruments (NFIs), the X-ray telescope (XRT; Burrows et al. 2005) and the UV/optical telescope (UVOT; Roming et al. 2005). Thanks to the unique ability of Swift to slew automatically after the BAT trigger, bursts are typically within the field of view of the narrow field instruments within a couple of minutes after the trigger. Thus, the XRT routinely provides positions with an accuracy of a few arc-seconds to the GRB community world-wide and measures the early X-ray light-curves and spectra of most GRB afterglows at which it is promptly pointed. Up to 2008 August 11, a total of 357 GRBs were detected by the BAT, of which 314 GRBs were observed by the XRT, although only 297 X-ray afterglows were thus detected by the XRT. Of these
burst observations, 253 were prompt slews (i.e. less than 300 s after the BAT trigger), and the XRT detected 94%![]() of those bursts (i.e. 238 afterglows).
of those bursts (i.e. 238 afterglows).
The Swift-XRT spectro-temporal observations associated with on-board and ground-based multi-wavelength observations have actively driven GRB science in the past three years by shedding new light on the physics of these objects. X-ray observations have revealed previously unexpected behaviour, including: multiple temporal breaks observed in some GRB light-curves inconsistent with the standard afterglow models (e.g. Zhang et al. 2006; Nousek et al. 2006; O'Brien et al. 2006; Willingale et al. 2007) and the discovery of X-ray flares observed in about ![]() of the Swift afterglows (e.g. Falcone et al. 2006, 2007;
Chincarini et al. 2007; Goad et al. 2007; Godet et al. 2007a, 2006; Burrows et al. 2007). Recent work has shown that some spectra cannot be fit by simple absorbed power-laws due to curvature, which can be interpreted as spectral breaks caused by the temporal shift of the energy peak through the XRT energy band during X-ray flares (e.g. GRB 051117A: Goad et al. 2007; and GRB 050822: Godet et al. 2007a). In some other cases, the presence of an extra component was suggested (see Butler 2007; Moretti et al. 2008a, for a general study) such as a blackbody component, which could be interpreted as: possible emission of a jet cocoon; the first-ever detection of a shock breakout from a massive star, likely a Wolf-Rayet, in the peculiar event GRB 060218 (Campana et al. 2006); possible photospheric emission for some X-ray flares in GRB 050822 (Godet et al. 2007a).
of the Swift afterglows (e.g. Falcone et al. 2006, 2007;
Chincarini et al. 2007; Goad et al. 2007; Godet et al. 2007a, 2006; Burrows et al. 2007). Recent work has shown that some spectra cannot be fit by simple absorbed power-laws due to curvature, which can be interpreted as spectral breaks caused by the temporal shift of the energy peak through the XRT energy band during X-ray flares (e.g. GRB 051117A: Goad et al. 2007; and GRB 050822: Godet et al. 2007a). In some other cases, the presence of an extra component was suggested (see Butler 2007; Moretti et al. 2008a, for a general study) such as a blackbody component, which could be interpreted as: possible emission of a jet cocoon; the first-ever detection of a shock breakout from a massive star, likely a Wolf-Rayet, in the peculiar event GRB 060218 (Campana et al. 2006); possible photospheric emission for some X-ray flares in GRB 050822 (Godet et al. 2007a).
More detailed X-ray spectral analyses have shed light on the environment of GRBs and the nature of the progenitor itself. Campana et al. (2007) showed evidence that the progenitor of the high redshift GRB 050904 at z=6.3 was located in a dense molecular cloud with a metallicity
![]() .
Using detailed modelling of the low-energy part of the X-ray spectrum, Campana et al. (2008a) showed that the progenitor of GRB 060218 was likely to be a massive star characterized by a fast stellar rotation and initial sub-solar metallicity giving, for the first time, direct evidence about the properties of GRB progenitors.
.
Using detailed modelling of the low-energy part of the X-ray spectrum, Campana et al. (2008a) showed that the progenitor of GRB 060218 was likely to be a massive star characterized by a fast stellar rotation and initial sub-solar metallicity giving, for the first time, direct evidence about the properties of GRB progenitors.
Thanks to its large energy band-pass and the ability to rapidly schedule targets, Swift is also a powerful tool for obtaining essential insights into the physics of non-GRB objects, especially transients. For example, the XRT has provided essential spectroscopic information since the start of the outburst of the recurrent nova RS Ophiuchi in 2006, enabling, for the first
time, detailed observations of the evolution of the Super-Soft Component in such an object (e.g. Bode et al. 2006; Hachisu et al. 2007). It also provided important spectroscopic information during the follow-up of several transient events (e.g., blazars: Tramacere et al. 2007; X-ray binaries: Esposito et al. 2007, Wijnands et al. 2007, Rykoff et al. 2007, Romano et al. 2007, Brocksopp et al. 2005; Comet 9P/Tempel 1: Willingale et al. 2006; active galactic nuclei: Molina et al. 2007, Tueller et al. 2008). From the beginning of 2008, the fraction of time spent on non-GRB science targets has been ![]()
![]() ,
and this will increase in the future.
,
and this will increase in the future.
![\begin{figure}
\par\includegraphics[height=5.5cm,width=8.cm,clip]{1157fig1.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg38.gif) |
Figure 1:
Energy resolution (
|
| Open with DEXTER | |
The results above show that X-ray spectroscopy is a powerful and essential tool for obtaining physical insights for celestial objects. These results depend on the intrinsic performance of the detector and the calibration of its spectral response. The XRT uses a front-illuminated e2v CCD-22, offering good spectroscopic performance with an energy resolution (FWHM) before launch of
135 eV at 5.9 keV (see also Fig. 1). The CCD-22 is a three phase frame transfer device, which utilises high resistivity (typically
![]() cm) silicon and an open electrode structure, originally designed for, and used in, the EPIC (European Photon Imaging Camera) MOS
cameras on-board XMM-Newton. The open electrode structure significantly improves the quantum efficiency of the device at low energy. The CCD imaging area consists of a 600
cm) silicon and an open electrode structure, originally designed for, and used in, the EPIC (European Photon Imaging Camera) MOS
cameras on-board XMM-Newton. The open electrode structure significantly improves the quantum efficiency of the device at low energy. The CCD imaging area consists of a 600 ![]() 600 pixel array with a pixel size of 40
600 pixel array with a pixel size of 40 ![]()
![]() .
Forty microns corresponds to 2.36 arcsec in the XRT field of view (e.g. Short et al. 2002). To mitigate the effects of pile-up, the CCD can automatically switch between different readout modes depending on the source brightness once the spacecraft is settled on the source (Hill et al. 2004, 2005):
.
Forty microns corresponds to 2.36 arcsec in the XRT field of view (e.g. Short et al. 2002). To mitigate the effects of pile-up, the CCD can automatically switch between different readout modes depending on the source brightness once the spacecraft is settled on the source (Hill et al. 2004, 2005):
- 1)
- photo-diode (PD) mode at the highest count rates with a 0.14 ms time resolution and no spatial information;
- 2)
- windowed Timing (WT) mode at moderate count rates, which uses a 200 column window covering the central 8 arcmin of the XRT field of view and provides 1D spatial imaging information. In that mode, the columns are clocked continuously to provide timing information in the trailed image along
each column with a 1.8 ms time resolution, at the expense of imaging information in this dimension (pixels are binned by a factor of 10 along columns);
- 3)
- at lower count rates, Photon Counting mode (PC), which provides 2D spatial imaging information, but with a 2.5 s time resolution.
The XRT effective area (EA) is made up of the response of the mirrors, the filter placed in front of the CCD detector to reduce optical and UV photon loading and the CCD detector response. The mirror and filter responses are included in the auxiliary response files (ARFs), while the CCD response is included in the redistribution matrix files (RMFs).
To avoid any misinterpretation in the spectral analysis, it is essential to have a good understanding of the instrument response and its operational limitations. The aim of this paper is to describe in detail our CCD response model used to compute the RMFs, the changes that have been made to the RMFs and ARFs since the launch (based on in-flight calibration) and the caveats to be aware of in the spectral analysis of XRT data when using the current (version 11) response files distributed in the CALDB release on 2008-06-25. An overview of the other aspects of the XRT calibration can be found in Campana et al. (2008b) and a detailed study of the XRT background can be found in Moretti et al. (2008b). This paper is organised as follows: Sect. 2 - we describe the physics implemented in our RMF code. We also briefly describe the spectroscopic performance of the RMFs in both PC and WT modes prior to launch using ground calibration data; Sect. 3 - we discuss the in-flight operation of the XRT and its impact on the calibration of the XRT response, the calibration program, and in detail post-launch changes made to the CCD spectral model (low-energy response, line shoulder, shelf, RMF redistribution) and the ARFs based on celestial target calibration; Sect. 4 - we present the spectroscopic performance of the XRT for several celestial targets compared to observations with other X-ray instruments, as well as caveats (line broadening due to the build-up of charge traps on the CCD and changes in the in-orbit operation of the CCD caused by raising the substrate voltage from 0 V to 6 V in 2007 August 30) for the spectral analysis when using the current RMFs and ARFs; Sect. 5 - we present the main conclusions of the paper.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{1157fig2.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg44.gif) |
Figure 2:
Architecture of the CCD response model used to compute the XRT RMFs. The RMFs contain 2400 input energy channels with a 5 eV energy width. In each energy channel,
|
| Open with DEXTER | |
2 Computation of the spectral response
![\begin{figure}
\par\includegraphics[height=12cm,width=14.cm,clip]{1157fig3.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg47.gif) |
Figure 3:
Pictures of the CCD-22 structure and geometry of a CCD-22 pixel as used in our spectral response code. ( Top left and right panels) Top and side view of a CCD-22 pixel, respectively. These images were obtained by a scanning electron microscope provided by e2v. The different parts of the pixel are shown on these two images. ( Bottom left and right
panels) Geometry of the CCD-22 pixel as used in our CCD response model (the dimensions are given in units of |
| Open with DEXTER | |
The XRT spectral response is based on a physical model describing the interaction of photons within the silicon bulk of a CCD-22 pixel via Monte-Carlo simulations. A Monte-Carlo simulator was developed at the University of Leicester in order to generate the RMFs for all the XRT readout modes (Short et al. 2002; Mukerjee et al. 2004). The CCD response model was refined by implementing ad-hoc corrections in our code based on the ground and in-flight calibration. We discuss here the main steps used to generate the RMFs.
2.1 RMF generation
Figure 2 shows the architecture of our CCD response model. To compute the RMFs, we stack simulated spectra of monochromatic X-rays using simple geometry of a CCD-22 pixel as input parameters, including the electrode structure, the finger and the open area (see Fig. 3) and the linear absorption coefficients of the different CCD compounds. The linear absorption coefficients used in our simulations include the effects of the rapid oscillatory X-ray Absorption Fine Structures (XAFS) just above the absorption edges of the CCD constituents (mainly N, O and Si) as measured by Owens et al. (1996a) for the JET-X CCD (see Fig. 4). It is essential to take them into account to obtain proper modelling of the spectral response around the edges.
2.1.1 Carrier generation and charge spreading
0.2-10 keV photons impinging on the detector have a high probability of interacting via the photoelectric effect. This results in the generation of a charge cloud with an initial charge Q0 given by:
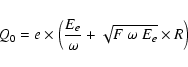 |
(1) |
where F and
The newly formed charge cloud has an initial 1![]() radius of
radius of
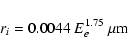 |
(2) |
assuming that the spatial distribution of the charge follows a Gaussian (Fitting et al. 1977). This charge cloud is collected in the buried channel in the depletion region after spreading in the bulk of the detector. The buried channel is defined as the potential well where the photo-generated charge will be collected and stored in a given CCD pixel between each readout. For the CCD-22, the buried channel covers the entire pixel size. The charge cloud may spread into more than one pixel, depending on its position with respect to the electrode structure and its depth, which is a function of the value of the linear absorption coefficients at the energy of the incoming photons (E) as follows:
where z,
The CCD pixel depth is divided into three regions:
- The depletion region:
where the charges experience the full effect of the electric field (where
- The field-free region:
where the charge no longer feels the effect of the electric field (i.e. a region wherewhere
where
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1157fig4.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg66.gif) |
Figure 4: Linear absorption coefficients of the CCD-22 compounds: (solid line) Si; (dotted line) SiO2; (dashed line) Si3N4. The small inset shows the XAFS just above the Si edge. The energy of the Si edge is slightly different depending on the compound considered. This is due to differences in the crystal lattice structure. |
| Open with DEXTER | |
- The substrate region:
in which most of the charge produced is lost by diffusion and recombination, because the electron diffusion length is much shorter than in the two other regions. The contribution to the charge cloud radius due to spreading in the substrate region is given by (McCarthy et al. 1995)where
The total 1![]() radius of the charge cloud reaching the buried channel is then given by the quadratic summation of the relevant radii assuming that the charge cloud profile due to radial diffusion is normally distributed:
radius of the charge cloud reaching the buried channel is then given by the quadratic summation of the relevant radii assuming that the charge cloud profile due to radial diffusion is normally distributed:
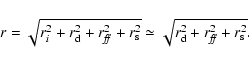 |
(8) |
The contribution of ri can be neglected with respect to that from the spreading radii
Figure 3 gives the thicknesses of these different layers as used in the CCD response model. The thickness of the depletion depth is an input parameter in our model. From quantum efficiency (QE) measurements performed at the Leicester calibration facility, we demonstrated that a
27 ![]() m-thick depletion depth matches the on-ground calibration data using a substrate voltage of
m-thick depletion depth matches the on-ground calibration data using a substrate voltage of
![]() V, as initially set in flight.
V, as initially set in flight.
2.1.2 Event recognition process
![\begin{figure}
\par\includegraphics[height=16cm,width=16cm,clip]{1157fig5.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg77.gif) |
Figure 5:
List of the XRT event grades: ( left) for PC mode, a 3 |
| Open with DEXTER | |
The spreading of the charge cloud over several pixels implies that it is essential to use an event grade recognition process to retrieve the right energy of the incoming photons. We use the same event grade recognition process as implemented in the ground analysis software ( XRTDAS
software package![]() ;
Capalbi et al. 2005).
;
Capalbi et al. 2005).
An event is formed when a pixel has an analogue-to-digital converted (ADC) charge greater than the event threshold (80 DN![]() ). This threshold is used to avoid pixels containing only noise from swamping the telemetry. In PC mode, the event data are telemetered as a
3
). This threshold is used to avoid pixels containing only noise from swamping the telemetry. In PC mode, the event data are telemetered as a
3 ![]() 3 pixel matrix centred on the pixel with the most charge. Only the surrounding pixels for which the charge is above the split event threshold (40 DN) are considered in the grade mapping, the other pixels being discarded. The split event threshold was fixed at 40 DN to minimise the increase of the sub-threshold charge losses which result in a wing on the low-energy side of the line profile, and hence to minimise the degradation of the energy resolution (see Sects. 2.1.3 and 3.3.3).
3 pixel matrix centred on the pixel with the most charge. Only the surrounding pixels for which the charge is above the split event threshold (40 DN) are considered in the grade mapping, the other pixels being discarded. The split event threshold was fixed at 40 DN to minimise the increase of the sub-threshold charge losses which result in a wing on the low-energy side of the line profile, and hence to minimise the degradation of the energy resolution (see Sects. 2.1.3 and 3.3.3).
Since the WT mode only offers 1D spatial imaging information (see Sect. 1), it is impossible to use a 3 ![]() 3 pixel matrix in WT mode to classify the X-rays events. Instead, a seven pixel vector centred on the pixel with the most charge is used. In WT mode, the central and split event thresholds are both set at 80 DN. Figure 5 shows the list of the 32 and 15 event grades which can be formed in PC and WT modes, respectively. The PC grades are similar to those defined for the XMM-Newton MOS data (Burrows et al. 2005).
3 pixel matrix in WT mode to classify the X-rays events. Instead, a seven pixel vector centred on the pixel with the most charge is used. In WT mode, the central and split event thresholds are both set at 80 DN. Figure 5 shows the list of the 32 and 15 event grades which can be formed in PC and WT modes, respectively. The PC grades are similar to those defined for the XMM-Newton MOS data (Burrows et al. 2005).
To eliminate events due to charged particles, and to obtain good energy resolution, we consider grades 0-12 in PC mode and grades 0-2 in WT mode as valid X-ray events. From Fig. 5, the WT grade 0 includes the PC grades 0, 1 and 3 (i.e. the mono-pixel and vertical split events in PC modes), while the WT grades 0-2 includes the good PC grades 0-12 as well as possible higher PC grades 15, 17, 19, 21, 23, 25-29.
The pre-launch RMFs (v006) were released for three grade selections (0, 0-4 and 0-12) in PC mode and two grade selections (0 and 0-2) in WT mode. This was to offer the user the choice of higher spectral resolution at the cost of lower effective area. The decision was made after launch not to upgrade the PC grade 0-4 RMFs after the release of the v007 response files, since the PC grade 0-12 RMF offers a higher quantum efficiency at high energy and its calibration was sufficiently good.
2.1.3 X-ray spectrum from monochromatic radiation
The X-ray event energy spectrum resulting from monochromatic radiation with an energy E significantly differs from a simple Gaussian. It consists of multiple components: a Gaussian photo-peak with a shoulder on the low energy side, a shelf extending to low energies, and, at the very lowest energies, the high-energy side of a noise peak above the on-board central event threshold (see Sect. 2.1.2). For photon energies above the Si K-shell edge (1.839 keV in the silicon bulk) two additional features appear: an escape peak of energy
![]() ,
and a Si K
,
and a Si K![]() fluorescence peak at
fluorescence peak at
![]() keV.
keV.
The DN value of the minimum energy threshold (thres) in the spectra depends on the mode, the grade selection and the settings for the event threshold and the split event threshold in the ground processing code. The default threshold configuration for PC mode is 80 DN and 40 DN, respectively, and for WT mode both are set to 80 DN. Therefore, in PC mode, the default minimum energy
threshold for grade 0 events is 80 DN while it is set at (80+40) DN for double split events, (
![]() )) DN for triple split events and (
)) DN for triple split events and (
![]() )) DN for quadruple split events. In WT mode, the minimum energy threshold is set at 80 DN and 80+80 DN for grade 0 and grades 1 and 2 events, respectively. The thres-values once expressed in units of eV (i.e.
)) DN for quadruple split events. In WT mode, the minimum energy threshold is set at 80 DN and 80+80 DN for grade 0 and grades 1 and 2 events, respectively. The thres-values once expressed in units of eV (i.e.
![]() where C0 and G (=10) are the multiplicative DN to PHA (pulse height amplitude) gain factor and the global PHA to PI (pulse invariant) gain factor, respectively - see Eq. (10)) slightly increased over time, since the gain coefficient C0 has increased
by about 3% from launch to June 2007 (see Fig. 12 and Sect. 3.2.2).
where C0 and G (=10) are the multiplicative DN to PHA (pulse height amplitude) gain factor and the global PHA to PI (pulse invariant) gain factor, respectively - see Eq. (10)) slightly increased over time, since the gain coefficient C0 has increased
by about 3% from launch to June 2007 (see Fig. 12 and Sect. 3.2.2).
At low energy, a large fraction of the photons interact at the interface between the SiO2 layer placed on top of the silicon bulk and the active silicon bulk itself. Short et al. (2002) measured the lost fraction of the total charge formed at that interface. This energy loss results in a low-energy wing in the line profile as well as a shelf extending to low energy. The effects of the surface charge losses start to become very significant below 0.5 keV, since the photo-peak disappears almost completely and the resulting line profile is shifted to lower energies (see Short et al. 2002). The authors proposed that the surface loss effect may be due to the charge-state of the surface oxide so that the oxide layer is charged enough in the etched regions (open electrode areas shown in white in the bottom left panel in Fig. 3) to cause a local turn-over of the potential (see Fig. 7 in Short et al. 2002). In this case, the charges formed near the oxide layer will move to the surface rather than to the buried channel. The surface charge losses are a function of the depth of interaction and the energy. To model this double dependency, the XRT energy range is divided into 12 energy bands (
![]() ). In each energy band, the
surface charge losses were initially defined by a set of linear functions
). In each energy band, the
surface charge losses were initially defined by a set of linear functions
![]() depending on the depth of interaction z inside the silicon bulk, the coefficients of the function
depending on the depth of interaction z inside the silicon bulk, the coefficients of the function
![]() being empirically derived from spectroscopic measurements performed at different energies at the Leicester calibration facility using radioactive elements.
being empirically derived from spectroscopic measurements performed at different energies at the Leicester calibration facility using radioactive elements.
At higher energies, when the photons interact more deeply in the CCD (above 2 keV), other processes start to become more important in the production of the shoulder and the shelf: (i) sub-threshold losses (see Sect. 3.3.3); (ii) diffusion, recombination and trapping in the bulk of the detector; (iii) inhomogeneity of the electric field in the depletion depth; these act in addition to the surface losses. The exact shape of the shoulder and the shelf depend on the readout mode (see Fig. 6 and the top panel in Fig. 7).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{1157fig6.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg85.gif) |
Figure 6:
Spectra from the Mn K |
| Open with DEXTER | |
2.2 Performance of the pre-launch RMFs
The XRT CCD was calibrated using the EPIC calibration facility at the University of Leicester, using sixteen discrete energies covering the 0.3-10 keV energy range. These measurements were used to interpolate and generate the redistribution component of the XRT RMFs. The RMFs were initially calibrated for a value of the substrate voltage of
![]() V, which was the value
used from launch to 2007 August 30 (see Sect. 4.3).
V, which was the value
used from launch to 2007 August 30 (see Sect. 4.3).
Table 1: Summary of the in-flight calibration targets used since the launch on 2004 November 20.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1157fig7.ps}\par\includegraphics[angle=-90,width=7cm,clip]{1157fig8.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg88.gif) |
Figure 7:
( Top panel) PC grade 0 spectrum measured at the Leicester
calibration facility from the Si K |
| Open with DEXTER | |
The pre-launch RMFs were computed to model the spectral response in the central region of the CCD, i.e. a window of 200 ![]() 200 pixels (a field of view of about 7.9
200 pixels (a field of view of about 7.9 ![]() 7.9 arcmin2). This area also corresponds to the area on the CCD where most of the GRB X-ray afterglows are located after the spacecraft slews.
7.9 arcmin2). This area also corresponds to the area on the CCD where most of the GRB X-ray afterglows are located after the spacecraft slews.
Although the pre-launch RMFs showed good agreement between the calibration data and the model in many circumstances, as displayed in the top panel of Fig. 7, there were still some modelling issues. The low-energy shoulder of the high-energy (E > 2-3 keV) line profiles and the shelf needed improvement (see the bottom panel in Fig. 7).
3 In-flight calibration
3.1 Calibration overview
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1157fig9.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg89.gif) |
Figure 8: CCD-22 simplified schematic diagram. The four 55Fe corner sources permanently illuminating areas of the CCD outside the field of view are shown as grey circles. |
| Open with DEXTER | |
Regular in-flight spectroscopic calibration observations of a set of well-known celestial objects are performed (with a frequency of about 6 months) in order to monitor changes in the response (see Table 1). The fraction of time spent on calibration since the launch is ![]()
![]() of
the total in-orbit time. In addition, we make use of four 55Fe calibration sources which are located in each corner of the CCD and which permanently illuminate a small fraction of the CCD area outside the XRT field of view as shown in Fig. 8. Before the focal plane camera assembly
(FPCA) door was opened, we also made use of an 55Fe calibration source located on the inside of the door, which illuminated the entire CCD imaging area.
of
the total in-orbit time. In addition, we make use of four 55Fe calibration sources which are located in each corner of the CCD and which permanently illuminate a small fraction of the CCD area outside the XRT field of view as shown in Fig. 8. Before the focal plane camera assembly
(FPCA) door was opened, we also made use of an 55Fe calibration source located on the inside of the door, which illuminated the entire CCD imaging area.
Many of our calibration targets are also observed by other X-ray observatories such as XMM-Newton, Chandra, Suzaku and RXTE, enabling us to perform cross-calibration campaigns. So far, five cross-calibration campaigns with the XMM-Newton EPIC cameras on variable sources have been made (see Table 1 and Sect. 4.1). We also use the set of stable calibration sources observed by other X-ray instruments to compare and improve the performance of our spectral response (see Table 1 and Sect. 4.1).
3.2 Energy scale offsets and origins
Before describing the post-launch improvements made in our CCD response model, we address an important issue related to energy scale offsets, since they can lead to misinterpretation of the data and hence strongly affect the modelling of the response, especially around the instrumental edges. Below, we discuss four different causes resulting in energy scale offsets and describe the solutions which were found to correct the XRT energy scale.
3.2.1 Evaluation of the bias level
In addition to thermal noise, each pixel charge will carry with it a fixed zero-point offset DN value, a random readout noise from the amplifier and the noise from camera electronics. The zero-point offset defines the bias level measured on the CCD. The amplifier readout noise and the electronic noise, however, affect the determination of the bias level, but we minimize those
contributions by averaging multiple bias measurements. In any case, the noise contributions should be much less than the measured offsets. In orbit, bias frames in PC mode and bias rows in WT mode are taken during each slew of the spacecraft to a new target before the beginning of an observation. For PC mode, the bias is computed on a pixel-by-pixel basis. Five 600 ![]() 600 pixel bias frames are taken, averaging each into the existing bias map using a ``running-mean'' algorithm that sets each pixel (x,y) to a new mean value computed as follows:
600 pixel bias frames are taken, averaging each into the existing bias map using a ``running-mean'' algorithm that sets each pixel (x,y) to a new mean value computed as follows:
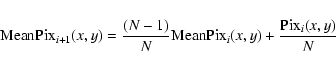
where N=3 is the running mean length and i=1,..., 5 is the frame count. For WT mode, the bias row is a vector of bias values, one for each column in the WT mode window (i.e. 200 columns). The bias row vector is computed over one image of 600 rows. A ``running-mean'' approximation is computed for each pixel x in each row according to the following equation:
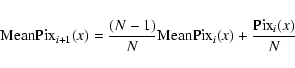
with N=3 and i corresponding to the row. The bias information is then used to correct on-board the subsequent frames of data during the XRT observations.
![\begin{figure}
\par {\hspace*{1cm}\includegraphics[width=6cm,clip]{1157fi10.ps}\hspace*{1cm}}
\par\includegraphics[width=8cm,clip]{1157fi11.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg93.gif) |
Figure 9: ( Top panel) Detector coordinate image showing the SNR Cas A when scattered optical light from the sunlit Earth is present on the detector (visible on the left side of the detector). ( Bottom panel) PC mode light-curve of the SNR Cas A in the 0.3-10 keV energy range for different snapshots and grade selections: 0, 1-4, 5-12 and 13-31. The light-curve was obtained before bias correction. The drop of the count rate in the PC grade 0 light-curve is due to the presence of scattered optical light from the sunlit Earth, which induces a grade migration from good grades (0-12) to higher grades. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=6cm,width=7cm,clip]{1157fi12.ps}\par\includegraphics[height=6cm,width=7cm,clip]{1157fi13.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg94.gif) |
Figure 10: ( Top panel) Comparison of the event energy spectra of the Si and S lines in the North (N) and South East (SE) knots of the SNR Cas A as observed by the XMM-Newton MOS cameras (N: black; SE: red) and the Swift-XRT (N: green, cyan; SE: blue, magenta). The green and blue crosses correspond to XRT/PC grade 0 data for which the bias was contaminated by optical light from the sunlit Earth. The data were processed with the v2.6 XRT software which does not correct for bias contamination. In this case, an energy scale offset is observed when compared with the XMM-Newton MOS spectra. The cyan and magenta crosses correspond to the same data processed with the XRT software including the task XRTPCBIAS, which corrects the data. ( Bottom panel) Swift-XRT WT grade 0-2 spectrum of RS Ophiuchi: (black) the data not corrected for the bias contamination and (red and blue) the data corrected using the modified task XRTWTCORR. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi14.ps}\par\includegraphics[angle=-90,width=7cm,clip]{1157fi15.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg95.gif) |
Figure 11:
( Top panel) WT grade 0-2 spectrum of the SNR Cas A in the energy band of the Si K |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1157fi16.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg96.gif) |
Figure 12:
( Top panel) Evolution of the gain C0 at a CCD temperature of -65 |
| Open with DEXTER | |
The bias level is mode dependent, and we have also seen observational evidence that the bias level can significantly vary even during a single snapshot on a celestial target (i.e. over ![]() 20 min). Variations of the measured bias level can be due to changes in the CCD temperature following some sky pointing directions. Shifts in the CCD bias level are also caused by roughly
sinusoidal temperature variations of
20 min). Variations of the measured bias level can be due to changes in the CCD temperature following some sky pointing directions. Shifts in the CCD bias level are also caused by roughly
sinusoidal temperature variations of ![]() 3
3 ![]() C during each 95 min orbit. The measured bias level can also be contaminated by scattered optical light from the sunlit Earth as shown in the top panel in Fig. 9 (see Beardmore et al. 2007, for more details). Scattered optical light from the sunlit Earth mainly affects PC mode because of its much longer frame accumulation time than WT mode, and seems to occur when the instrument is pointed near the sunlit Earth horizon. Changes in the bias level in both WT and PC modes result in energy scale offsets (see Fig. 10).
C during each 95 min orbit. The measured bias level can also be contaminated by scattered optical light from the sunlit Earth as shown in the top panel in Fig. 9 (see Beardmore et al. 2007, for more details). Scattered optical light from the sunlit Earth mainly affects PC mode because of its much longer frame accumulation time than WT mode, and seems to occur when the instrument is pointed near the sunlit Earth horizon. Changes in the bias level in both WT and PC modes result in energy scale offsets (see Fig. 10).
In order to correct the bias level on the ground, and hence restore the energy scale (see Fig. 10), the task XRTWTCORR, for WT mode, was enabled in the XRTDAS software package (Swift software v.2.6). For PC mode, a new task XRTPCBIAS was developed and released with Swift software v.2.7.
In addition to producing energy scale offsets, in some extreme cases scattered optical light in PC mode can induce a significant grade migration from good grades (grades 0-12) to higher rejected grades, resulting in an apparent loss of counts in the light-curve (see the bottom panel in Fig. 9). In these extreme cases, the XRTPCBIAS task will not be able completely to correct the bias level and a residual energy scale offset will be still present in the spectra.
3.2.2 Increase of charge transfer inefficiency
CCD detectors provide good X-ray imaging and spectroscopic performance. However, the increase of charge transfer inefficiency (CTI) over time due to radiation damage is a fundamental limitation of CCD technology. Due to the effects of CTI, charge is lost during the readout process so that
the remaining charge Q reaching the output amplifier after ![]() transfers in the serial direction and
transfers in the serial direction and ![]() transfers in the parallel direction is
transfers in the parallel direction is
where Q0 is the initial charge and CTI
Table 2: Summary of the releases of the XRT post-launch gain files.
The XRT gain file takes into account the effect of CTI as follows:
where x and y correspond to the position of the event in the CCD imaging area. G=10 is the global PHA to PI gain factor. C0 is the multiplicative DN to PHA gain factor, while C1,2 = C0
Since launch, the evolution of serial and parallel CTI and the gain over time have been monitored using the four corner calibration sources (see Fig. 8). The gain C0 is given by the gain of the bottom left corner source CS3 closest to the output amplifier, as this does not suffer from CTI loss in the imaging area. C0 thus includes both the output amplifier gain and the degradation in the gain caused by charge loss during the frame-store transfer. CTI![]() is measured using corner source pair CS3 and CS4, while CTI
is measured using corner source pair CS3 and CS4, while CTI![]() measured using corner source pair CS1 and CS3. Figure 12 shows the evolution of the gain C0 (from 2.529 just after launch to 2.625 in June 2007) and the CTI
measured using corner source pair CS1 and CS3. Figure 12 shows the evolution of the gain C0 (from 2.529 just after launch to 2.625 in June 2007) and the CTI
![]() values over time. Figure 12 shows a jump in gain C0 around MET (Mission Elapsed Time) 2.1
values over time. Figure 12 shows a jump in gain C0 around MET (Mission Elapsed Time) 2.1 ![]() 108 s due to the substrate voltage change from
108 s due to the substrate voltage change from
![]() V to 6 V (see Sect. 4.3). There also is a jump in CTI around MET 1.6
V to 6 V (see Sect. 4.3). There also is a jump in CTI around MET 1.6 ![]() 108 s; the origin of this jump is however unknown. The correction of the data from the effects of CTI is illustrated in the bottom
panel of Fig. 11. These CTI values were implemented in the PC and WT gain files from version 007 and onwards (see Table 2).
108 s; the origin of this jump is however unknown. The correction of the data from the effects of CTI is illustrated in the bottom
panel of Fig. 11. These CTI values were implemented in the PC and WT gain files from version 007 and onwards (see Table 2).
3.2.3 The effect of temperature
The XRT was designed to cool the CCD to a nominal operating temperature of -100![]() C using a thermo-electronic cooler (TEC). However, the TEC power supply system apparently failed shortly after launch, and the XRT has to rely on passive cooling via a heat pipe and radiator, in combination with enhanced management of the spacecraft orientation to reduce the radiator view of the
sunlit Earth. The XRT is now operated with CCD temperatures varying between -75 to -52
C using a thermo-electronic cooler (TEC). However, the TEC power supply system apparently failed shortly after launch, and the XRT has to rely on passive cooling via a heat pipe and radiator, in combination with enhanced management of the spacecraft orientation to reduce the radiator view of the
sunlit Earth. The XRT is now operated with CCD temperatures varying between -75 to -52 ![]() C (see Kennea et al. 2007, for more details), though new GRBs occasionally cause it to exceed -52
C (see Kennea et al. 2007, for more details), though new GRBs occasionally cause it to exceed -52 ![]() C.
C.
Since the gain of the CCD output FET (Field Effect Transistor) is sensitive to the temperature, the reduced temperature stability required the introduction of a temperature dependency in the gain expression in order to restore the XRT energy scale. In addition to the K![]() and K
and K![]() fluorescent lines of the corner source data, we used the supernova remnant Cas A, because its spectrum shows intense silicon (1.86 keV) and sulphur (2.45 keV) lines as well as an iron (6.6 keV) line. The gain coefficient C0 in Eq. (10) was computed at two CCD temperatures other than the -100
fluorescent lines of the corner source data, we used the supernova remnant Cas A, because its spectrum shows intense silicon (1.86 keV) and sulphur (2.45 keV) lines as well as an iron (6.6 keV) line. The gain coefficient C0 in Eq. (10) was computed at two CCD temperatures other than the -100 ![]() C used during the ground calibration: -65
C used during the ground calibration: -65 ![]() C and -48
C and -48 ![]() C using in orbit Cas A data. The ground data processing software linearly interpolates between tables of gain coefficients for these three different temperatures to determine the
correct value to use for a given observation
C using in orbit Cas A data. The ground data processing software linearly interpolates between tables of gain coefficients for these three different temperatures to determine the
correct value to use for a given observation![]() . These temperature-dependent values of C0 were used to compute the coefficients C1,2 as well (see Sect. 3.2.2). The linear slope characterizing the
gain change as a function of temperature from -65
. These temperature-dependent values of C0 were used to compute the coefficients C1,2 as well (see Sect. 3.2.2). The linear slope characterizing the
gain change as a function of temperature from -65 ![]() C to -48
C to -48 ![]() C is 0.00117 eV DN-1
C is 0.00117 eV DN-1 ![]() C-1. This corresponds to a
C-1. This corresponds to a ![]() 7 eV variation in the energy scale at 1.5 keV for a 10
7 eV variation in the energy scale at 1.5 keV for a 10 ![]() C temperature variation. This temperature dependency on the gain was included in the v005 release of the PC and WT gain files (see Table 2).
C temperature variation. This temperature dependency on the gain was included in the v005 release of the PC and WT gain files (see Table 2).
3.2.4 Comparison of the WT and PC energy scale
We found that even after correcting the data for the various sources of energy scale offsets discussed in previous sections, there was still a slight systematic mismatch between the WT and PC energy scales (see the top panel in Fig. 13). We estimated the systematic offset to be 17.6 eV, based on the comparison of the line centroids between WT and PC Cas A spectra, as well as the use of the XMM-RGS model to fit the XRT/WT spectra of the SNR E0102-723 using the gain command within Xspec (Arnaud 1996). This energy shift appears to be independent of time, temperature and energy. The setting of the offset term C3 in Eq. (10) at 17.6 eV in the WT gain file was shown significantly to improve the WT energy scale (see the bottom panel in Fig. 13). This new v008 WT gain file was released on 2008 June 25 (see Table 2). The origin of the energy offset in WT mode is unclear and still under investigation.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1157fi17.ps}\vspace*{5mm}
\includegraphics[angle=-90,width=7.5cm,clip]{1157fi18.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg106.gif) |
Figure 13:
Spectra of the entire SNR Cas A in WT mode at different epochs:
(black) 2005-02-16; (red) 2006-04-20; (green) 2007-06-06. The blue line indicates the expected energy centroid of the Si and S K |
| Open with DEXTER | |
3.3 Improvements to the response model
We discuss in this section the improvements made to the CCD response model based on experiences from in-flight calibration. Table 3 summarises the improvements made to the response files and the corresponding release number.
Table 3: Summary of the releases of the XRT post-launch RMFs.
3.3.1 The low-energy response
Shortly after launch, it became apparent that the low energy (E < 0.5 keV) response model could be improved. Figure 14 shows that the PC grade 0 spectrum of the soft neutron star RX J1856.4-3754 (the black curve) is poorly fitted when the v007 RMF is used. A CONST*WABS*(BBODYRAD+BBODYRAD) model with the spectral parameters fixed to the values given in Beuermann et al. (2006, i.e.
![]() ,
kT1 = 62.8 eV and
kT2 = 32.3 eV) was used for the fit. The lowest temperature black-body component has a minor impact in the XRT energy range. It was introduced by Beuermann et al. (2006) to fit the EUVE data as well as the Chandra data. Below 0.3 keV, the modelled line profile and its energy centroid are strongly dependent on the estimate of the charge losses at the CCD surface. As explained in Sect. 2.1.3, these charge losses are a function of energy and location of interaction of incoming photons. To model these charge losses better, we used the semi-empirical formalism
described in Popp et al. (2000) to describe the loss function
,
kT1 = 62.8 eV and
kT2 = 32.3 eV) was used for the fit. The lowest temperature black-body component has a minor impact in the XRT energy range. It was introduced by Beuermann et al. (2006) to fit the EUVE data as well as the Chandra data. Below 0.3 keV, the modelled line profile and its energy centroid are strongly dependent on the estimate of the charge losses at the CCD surface. As explained in Sect. 2.1.3, these charge losses are a function of energy and location of interaction of incoming photons. To model these charge losses better, we used the semi-empirical formalism
described in Popp et al. (2000) to describe the loss function
![]() in our CCD response model as follows:
in our CCD response model as follows:
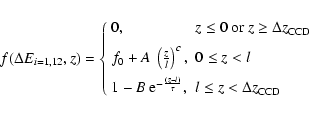
where f0, c, l and
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi19.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg114.gif) |
Figure 14: Comparison of the low-energy response between v007 (black) and v008 (red) RMFs using the spectrum of the soft neutron star RX J1856.4-3754 in PC mode for grade 0 events. We used a CONST*WABS*(BBODYRAD+BBODYRAD) model with the spectral parameters fixed to the values given in Beuermann et al. (2006). |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=7cm,clip]{1157fi20.ps}...
...ce*{3mm}
\includegraphics[angle=-90,width=7cm,clip]{1157fi23.ps} }\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg115.gif) |
Figure 15:
Best fits of absorbed sources (
|
| Open with DEXTER | |
3.3.2 The modelling of the shelf from photons above  2 keV
2 keV
Before the release of the v009 RMFs, the spectral fits of heavily absorbed sources (with ![]() typically larger than 1022 cm-2) in either PC or WT mode showed an underestimation of the modelled redistributed counts at low energies corresponding to the shelf (see the red curves in
Fig. 15). As discussed in Sect. 2.1.3, the physical origin of the shelf, and hence its modelling, is complex. To improve the CCD response model, we decided to rescale the shelf for incident photons above 2 keV, since this is a straightforward approach. The result of this rescaling significantly improves the residuals at low energy when fitting spectra of heavily absorbed
sources in both modes (see the black curves in Fig. 15). While the rescaling of the PC shelf did not change the QE at high energy because the shelf is at least two orders of magnitude below the photo-peak, the rescaling of the shelf in WT mode increased the QE by
typically larger than 1022 cm-2) in either PC or WT mode showed an underestimation of the modelled redistributed counts at low energies corresponding to the shelf (see the red curves in
Fig. 15). As discussed in Sect. 2.1.3, the physical origin of the shelf, and hence its modelling, is complex. To improve the CCD response model, we decided to rescale the shelf for incident photons above 2 keV, since this is a straightforward approach. The result of this rescaling significantly improves the residuals at low energy when fitting spectra of heavily absorbed
sources in both modes (see the black curves in Fig. 15). While the rescaling of the PC shelf did not change the QE at high energy because the shelf is at least two orders of magnitude below the photo-peak, the rescaling of the shelf in WT mode increased the QE by ![]()
![]() at 6 keV. This increase of the high-energy QE in WT mode also gives a better agreement with
expectation of the grade ratios between the PC and WT modes (see Sect. 3.4). This new modelling was included in the release of v009 RMFs.
at 6 keV. This increase of the high-energy QE in WT mode also gives a better agreement with
expectation of the grade ratios between the PC and WT modes (see Sect. 3.4). This new modelling was included in the release of v009 RMFs.
![\begin{figure}
\par\includegraphics[angle=-90,width=6.8cm,clip]{1157fi24.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg118.gif) |
Figure 16: Plot of the PC quantum efficiency using v007 RMF for: grade 0-12 (red) and grade 0 (black). |
| Open with DEXTER | |
3.3.3 Origin of the low-energy shoulder from high-energy photons
For low-energy photons (below about 2 keV), the low-energy shoulder of the line profile can be modelled successfully by charge losses at the interface between silicon and oxide layer. However, the same process cannot completely explain the low-energy shoulder seen in the line profile of high-energy photons. Hence, the pre-launch PC and WT RMFs (v006) were not able fully to model the line profile for high-energy photons (see the bottom panel in Fig. 7).
Tests performed after launch showed that an artificial increase of the split threshold in the CCD response model results in an increase of sub-threshold losses, and hence a better modelling of the shoulder. This empirical technique was implemented in the v007 RMFs. Even if the global result was to improve significantly the residuals around the shoulder (see Fig. 6a in Osborne et al. 2005), this technique was not entirely satisfactory since residuals were still present and the physical origin was unidentified. The other drawback was that the QE curve in PC mode showed discontinuities (smaller than ![]() )
due to the use of different values of the threshold depending on the energy
range (see Fig. 16), although these small discontinuities had no noticeable impact on the spectral fitting.
)
due to the use of different values of the threshold depending on the energy
range (see Fig. 16), although these small discontinuities had no noticeable impact on the spectral fitting.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1157fi25.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg120.gif) |
Figure 17: PC grade 0-12 spectrum of the 55Fe source on the XRT camera door fitted using the v009 RMF. The low energy shoulders of the lines are now correctly modelled using the Pavlov & Nousek formalism (compare to Fig. 7 lower panel). |
| Open with DEXTER | |
Pavlov & Nousek (1999) have stressed that when a photon interacts in the field-free region, the resulting charge cloud no longer has the profile of a 2D Gaussian, because it experiences free diffusion in this region before being distorted when penetrating the depletion region where the charge is collected. The authors gave an analytical formalism to describe the resulting shape of the charge cloud as a function of the depth of interaction. The resulting profile shows more extended wings which naturally favour the increase of sub-threshold losses for a given threshold value. The implementation of the Pavlov & Nousek formalism in our CCD response model gives good results as shown in Fig. 17. This new modelling was included in the release of v009 RMFs.
3.3.4 Feature around 0.9-1.0 keV in WT mode
Fits of high statistical quality WT spectra have revealed 10% systematic residuals around 0.9-1.0 keV, as shown in Fig. 18. An ad-hoc dip was added to the WT v008-v010 ARFs around 0.9 keV in order to suppress these residuals. However, this approach was not entirely satisfactory. These systematic residuals are due to a RMF redistribution issue. Indeed, as explained in Sect. 2.1.3, the surface charge losses are modelled by a loss function f so that its parameters are different in different energy segments. 1 keV corresponds to a boundary between two energy segments for which there is a slight discontinuity in the description of the loss function. We modified the parameters of the loss function in the 1-2 keV range in order slightly to change the monochromatic line input profile, as shown in Fig. 19 for 1.2 keV photons. New WT grade 0 and 0-2 RMFs (i.e. v011) were computed using this new description. These v011 RMFs give very good performance as shown by the red residuals in Fig. 18 (also see Sect. 4.1).
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi26.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg121.gif) |
Figure 18:
WT grade 0-2 spectrum of Mkn 421 from June 2006 data fitted using the v010 (black) and v011 (red) RMFs. The residuals around 0.9-1.0 keV (black points) are due to a RMF redistribution issue in v007-v010 WT RMFs. The use of the new v011 WT RMFs including a slight change in the loss function between 1 and 2 keV gives flatter residuals in this region (red
points). The spectral model is an absorbed bending power-law with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi27.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg122.gif) |
Figure 19:
Gaussian models with a value of
|
| Open with DEXTER | |
3.4 Investigation of the QE shape from in-flight calibration
3.4.1 Overview of the QE calibration
The pre-launch QE was calibrated using measurements across the XRT energy range (0.3-10 keV) made at the Leicester calibration facility. However, some of these measurements were corrupted during the data taking process indicating that some of the low energy QE values were not valid.
It is not straightforward to obtain a direct measure of the QE in orbit, since the overall instrument spectral response depends on the mirror, filter transmission and CCD responses. Early fitting results suggested that the effective area needed to be rescaled between modes and grade selection due to QE uncertainties. It was also necessary to introduce corrections around the silicon and oxygen edges to obtain flat residuals when fitting spectra in both PC and WT mode. As discussed in Sect. 3.2, the correction around the oxygen edge was eventually found to be needed due to energy offsets in both modes.
We discuss below possible explanations accounting for the changes implemented in the ARFs and how they can be transfered to the CCD response model.
3.4.2 The silicon K edge and the low-energy QE shape
edge and the low-energy QE shape
Since the detector consists of silicon bulk, and the effective area has a
maximum in the 1.5-2.2 keV energy band, it is essential to take special care
when modelling the Si K![]() edge (1.839 keV).
edge (1.839 keV).
Fits of several bright sources in both WT and PC modes using pre-launch RMFs demonstrated that the modelling of the silicon edge was not completely correct, as shown by the black residuals below 2 keV in Fig. 20 for WT mode. The residuals above 2.2 keV are due to an improper modelling of the Au M-shell edge region (2.0-3.5 keV) in the theoretical ARF. This ARF is made of the filter transmission response SWXFTRANS20010101V005.FITS and the effective area (v004), which is computed by a ray-tracing code (Cusumano et al. 2005).
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi28.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg123.gif) |
Figure 20:
Best fits of the WT grade 0 spectrum of Mkn 421 using the WT grade 0 v011 RMF together with the theoretical ARF (black) and the new ARF v011 (red) which includes the correction of the CCD QE just above the Si K |
| Open with DEXTER | |
Initially, a correction was implemented in the v007-v010 PC and WT ARFs to flatten the residuals in the 1.8-2.2 keV energy range. However, that correction suffers from the effects of energy scale offsets which could not be entirely corrected at those times. Since then, we have been able to correct the XRT data from these effects (see Sect. 3.2). This enabled us to establish that the problem was related to an over-prediction of the QE in our CCD response just above the Si K![]() edge (1.84-2.2 keV) rather than a redistribution issue. A straightforward solution to correct the QE above the Si edge was to implement a correction based on the XMM-MOS QE curve, which shows a deeper profile at these energies. Unlike the Swift-XRT, the XMM/MOS QE from the XMM-SAS 7.1.2 was calibrated with a synchrotron beam in Saclay, allowing for accurate measurements around the Si edge. This correction, along with a correction of the Au edge region (2.2-4 keV) in the ARFs produced after launch, gives good results in WT mode (see the red curve in Fig. 20). A similar correction was implemented in the new v011 PC ARFs.
edge (1.84-2.2 keV) rather than a redistribution issue. A straightforward solution to correct the QE above the Si edge was to implement a correction based on the XMM-MOS QE curve, which shows a deeper profile at these energies. Unlike the Swift-XRT, the XMM/MOS QE from the XMM-SAS 7.1.2 was calibrated with a synchrotron beam in Saclay, allowing for accurate measurements around the Si edge. This correction, along with a correction of the Au edge region (2.2-4 keV) in the ARFs produced after launch, gives good results in WT mode (see the red curve in Fig. 20). A similar correction was implemented in the new v011 PC ARFs.
Keay et al. (1995) stressed that the QE shape just above the Si edge was strongly dependent on the electrode structure and composition of their JET-X CCD. They showed that the silicon contributes 65% of the QE shape above the edge, while the oxide and nitride of silicon contribute at 28% and 7%, respectively. As shown in Fig. 3, the description of the electrode structure in the CCD pixel geometry used to generate the XRT RMFs is relatively simple. In reality, there is an overlap of three different electrodes. An explanation for the QE over-prediction just above the silicon edge could be that the thicknesses of the different materials in the CCD geometry need to be more accurately specified. However, variation in thickness of the Si and SiO2 layers in the electrode and finger structures did not allow us to converge towards adequate thickness values for these layers to fully model the QE just above the silicon edge.
Nevertheless, from in-flight calibration we noticed that the total effective area at low energy needs to be decreased in both WT and PC modes to obtain correct flux levels and spectral parameters. Again, the electrode thicknesses appeared to be under-specified, since more low-energy photons will be stopped in the finger and electrode structures.
![\begin{figure}
\par {\hspace*{5mm}\includegraphics[width=6cm,clip]{1157fi29.ps}\...
...*{5mm}}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi30.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg124.gif) |
Figure 21:
( Top panel) Drawing showing the changes in the geometry of the
finger and channel stop, corresponding to a reduction of the open area by |
| Open with DEXTER | |
Another possible explanation accounting for the QE reduction at low-energy is that the etching of the electrode and finger structure did not result in the designed electrode widths, and some residual material was left as shown in Fig. 3. The residual material acts as an extra absorption layer for low-energy photons and so reduces the QE at low energy. As a test we
reduced the open electrode area by slightly increasing the channel stop width (by ![]() m) and the finger as shown in Fig. 21 (top panel), corresponding to an open area reduction of
m) and the finger as shown in Fig. 21 (top panel), corresponding to an open area reduction of ![]() .
The bottom panel in Fig. 21 shows a comparison of the WT grade 0-2 QE curve when using the new geometries (in red and green) and that from the WT grade 0-2 RMF v010
(in black). A less than 10% decrease of the QE is obtained at the energy of the oxygen edge (0.543 keV). This is consistent with the ad-hoc reduction implemented in the WT v007-v010 ARFs.
.
The bottom panel in Fig. 21 shows a comparison of the WT grade 0-2 QE curve when using the new geometries (in red and green) and that from the WT grade 0-2 RMF v010
(in black). A less than 10% decrease of the QE is obtained at the energy of the oxygen edge (0.543 keV). This is consistent with the ad-hoc reduction implemented in the WT v007-v010 ARFs.
New WT ARFs (v011) were created by rescaling the theoretical ARF below 2 keV using the green QE curve in the lower panel in Fig. 21 and by introducing the CCD QE correction just above the Si K![]() edge as discussed above, while the Au M-shell region was corrected using celestial continuum sources. These new WT grade 0 and 0-2 ARFs have similar shapes except
in the 1.5-1.84 keV energy range where the WT grade 0-2 ARF is rescaled down
by less than 2% with respect to the WT grade 0 ARF in order to flatten residuals below 2% (see Fig. 3 in Godet et al. 2008). Figures 20 (red curve) and 23 show WT spectra of Mkn 421 fitted using an absorbed bending power-law and the new v011 response
files. This plot shows the very good performance of the v011 WT RMFs/ARFs, since the residuals across the 0.3-10 keV energy range are better than 3% and the systematic errors are less than 2% (also see Sect. 4.1).
edge as discussed above, while the Au M-shell region was corrected using celestial continuum sources. These new WT grade 0 and 0-2 ARFs have similar shapes except
in the 1.5-1.84 keV energy range where the WT grade 0-2 ARF is rescaled down
by less than 2% with respect to the WT grade 0 ARF in order to flatten residuals below 2% (see Fig. 3 in Godet et al. 2008). Figures 20 (red curve) and 23 show WT spectra of Mkn 421 fitted using an absorbed bending power-law and the new v011 response
files. This plot shows the very good performance of the v011 WT RMFs/ARFs, since the residuals across the 0.3-10 keV energy range are better than 3% and the systematic errors are less than 2% (also see Sect. 4.1).
3.4.3 Discrepancy in the effective area between PC and WT modes
We expect that differences in the effective area between PC and WT modes would be due to the differences in the event grading in these two modes. However, it was necessary to scale down the effective area in PC mode (for both grade 0 and 0-12) by a factor larger than expected from the simple differences in the event grading, in order to reproduce the correct flux levels for the same
calibration targets (see the top panel in Fig. 22; see Sect. 3.2 in Godet et al. 2008). Indeed, while the shape of the PC grade 0-12 effective area is similar to that of the WT grade 0-2 effective area above the Si K![]() edge (as expected from the event grading), the WT grade 0 effective area is larger than the PC grade 0-12 effective area below the Si K
edge (as expected from the event grading), the WT grade 0 effective area is larger than the PC grade 0-12 effective area below the Si K![]() edge. The event grading in PC and WT mode implies the opposite, since WT grade 0 events only contain PC grade 0, 1 and 3 events. The reason why the PC grade 0-12 effective area is less than the WT grade 0 effective area below
edge. The event grading in PC and WT mode implies the opposite, since WT grade 0 events only contain PC grade 0, 1 and 3 events. The reason why the PC grade 0-12 effective area is less than the WT grade 0 effective area below ![]() 1.84 keV remains unclear.
1.84 keV remains unclear.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1157fi31.ps}\par\includegraphics[width=7cm,clip]{1157fi32.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg126.gif) |
Figure 22:
( Top panel) Comparison of the XRT total effective area (EA) in PC and WT mode using the v011 response files. The PC grade 0 EA is very low when compared to the PC grade 0-12 and WT EA even at low energy (E < 1 keV) where we expect to have a similar QE level whatever the mode and grade selection. Below |
| Open with DEXTER | |
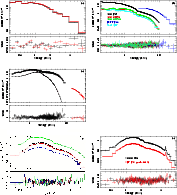 |
Figure 23:
Plots showing the best fits to different celestial sources when using the v011 PC and WT response files. a) WT grade 0 (black) and grade 0-2 (red) spectra of the blazar Mkn 421 observed in June 2006. The spectral model is an absorbed bending power-law (i.e. WABS * exp[- |
| Open with DEXTER | |
There is also a difference in the effective area at low energy (below 0.5 keV)
between the PC grade 0 and WT grade 0 effective areas. The fact that the WT
grade 0 events contain the PC grade 0, 1 & 3 events may account for the
discrepancy. However, the lower panel in Fig. 22 shows that
there are some differences in the Cas A spectra between WT grade 0 and PC
grades 0+ 1 + 3 in the 1-3 keV band. To extract these spectra, we used 2005
data collected prior to the apparition of the bad columns, and the data were
processed using the same central (80 DN) and split (80 DN) event
thresholds. Below ![]() keV, the differences observed between the two
spectra may be partially due to differences in the kernel redistribution
between the modes (see Fig. 6). That suggests that the
observed differences in effective area at low energy cannot be due to simple
differences in the event grading.
keV, the differences observed between the two
spectra may be partially due to differences in the kernel redistribution
between the modes (see Fig. 6). That suggests that the
observed differences in effective area at low energy cannot be due to simple
differences in the event grading.
4 In flight spectroscopic performance and caveats
We discuss in this section the in-flight spectroscopic performance of the v011 response files when fitting data collected at a substrate voltage of
![]() V. For all the fits shown below, the PSF and exposure map corrections were taken into account in the ARFs using the version 5.5 of the task XRTMKARF of the XRTDAS software package (Capalbi
et al. 2005). We compare the fitting results with those found using other in-orbit X-ray instruments. We also discuss current caveats in the XRT spectral response: i) the line broadening due to the build-up of charge traps on the CCD over time and methods to handle it; ii) the impact of the permanent increase of the substrate voltage from 0 V to 6 V on the performance of the
v011 response files.
V. For all the fits shown below, the PSF and exposure map corrections were taken into account in the ARFs using the version 5.5 of the task XRTMKARF of the XRTDAS software package (Capalbi
et al. 2005). We compare the fitting results with those found using other in-orbit X-ray instruments. We also discuss current caveats in the XRT spectral response: i) the line broadening due to the build-up of charge traps on the CCD over time and methods to handle it; ii) the impact of the permanent increase of the substrate voltage from 0 V to 6 V on the performance of the
v011 response files.
Table 4: Summary of the spectral parameters obtained when fitting Swift-XRT, XMM-Newton, Chandra and RXTE data for several continuum sources.
Table 5: The second part of Table 4.
4.1 Spectroscopic performance
Figure 23 (panel a) shows the best fit of the high statistical quality WT spectra of the blazar Mkn 421 observed in June 2006 using the v011 response files. Each spectrum contains more than 106 counts. The residuals across the XRT energy range are below 3%. The fits of high statistical quality PC spectra show that residuals are less than 5% across the XRT energy range (see Godet et al. 2008).
The existence of several X-ray instruments (XMM-MOS, XMM-PN, Chandra, RXTE-PCA, Suzaku-XIS) covering an energy band similar to that of the XRT enabled us to perform cross-calibration using different continuum and line sources (see Fig. 23 panels b, d and e and Table 4; see Plucinsky et al. 2008, for a cross-calibration work on the SNR E0102-723). Figure 23 shows that the XRT spectral fit residuals are comparable with those of other instruments. The spectral parameters derived using XRT data are consistent with those derived using XMM-Newton, Chandra and RXTE data (see Table 4). The XRT fluxes from PC grade 0 events seem to be slightly higher up to 7% when compared to those found from XRT PC grade 0-12 and other instruments, indicating that the PC grade 0 effective area may need to be rescaled in the future. The WT grade 0 and grade 0-2 fluxes derived from the fits of our WT calibration sources agree with each other within the error bars (see Table 4).
The spectral analysis of joint BAT-XRT GRB spectra during overlapping time intervals showed relatively good agreement between the two instruments, within 10% in most cases. Figure 23 (panel c) shows the joint fit of the BAT and XRT data of Sco X-1. The data were fitted using a CONST*WABS(BBODYRAD+COMPTT) model. The constant factor
( CONST) was fixed to 1 for the XRT data and left as a free parameter for the BAT data ( CONST = 0.93 ![]() 0.04, the errors being given at 2.71
0.04, the errors being given at 2.71![]() ). The residuals observed for the XRT spectrum in Fig. 23 (panel c) above 8 keV correspond to Ni and Au L-shell fluorescence. Discrepancies larger than 10% between the BAT and XRT flux normalisation and/or large residuals at high-energy (above 5 keV) may mean that: i) the spectral model used is not suitable to fit the data; ii) the XRT data may be piled-up (pile-up is dependent on the spectral shape of the source. However, a rough limit for pile-up to become an issue is 100 counts s-1 in WT mode and 0.6 counts s-1 in PC mode for powerlaw-like spectra); iii) instrumental lines such as Ni K
). The residuals observed for the XRT spectrum in Fig. 23 (panel c) above 8 keV correspond to Ni and Au L-shell fluorescence. Discrepancies larger than 10% between the BAT and XRT flux normalisation and/or large residuals at high-energy (above 5 keV) may mean that: i) the spectral model used is not suitable to fit the data; ii) the XRT data may be piled-up (pile-up is dependent on the spectral shape of the source. However, a rough limit for pile-up to become an issue is 100 counts s-1 in WT mode and 0.6 counts s-1 in PC mode for powerlaw-like spectra); iii) instrumental lines such as Ni K![]() and K
and K![]() and Au L-shell fluorescence lines may be present above 8 keV (see Moretti et al. 2008b).
and Au L-shell fluorescence lines may be present above 8 keV (see Moretti et al. 2008b).
Our current understanding of the XRT response at
![]() V implies a systematic error of less than 3% in both WT and and PC mode in the 0.3-10 keV energy band and better than 10% in absolute flux (see Godet et al. 2008).
V implies a systematic error of less than 3% in both WT and and PC mode in the 0.3-10 keV energy band and better than 10% in absolute flux (see Godet et al. 2008).
4.2 Line broadening
In Sect. 3.2.2, we discussed the effect of the increase in CTI (due to charge traps too shallow to be individually identified) which can cause an energy scale change if not corrected. Besides this CTI, there is also a build-up of deeper charge traps due to high-energy proton and radiation damage to the CCD (the imaging area, the store frame area and the serial register), which dominate the line broadening observed in XRT data (see Fig. 11). The FWHM at 1.86 keV in the Cas A spectra has degraded from 105 eV in February 2005 to 131 eV in June 2007. Over the same interval, a 44% width increase was measured at 5.9 keV from the on-board calibration sources. The most serious of these charge traps can cause a loss of up to 350 eV from the incident X-ray energy.
Since launch, regular observations of the soft neutron star RX J1856.4-3754 have enabled us to monitor any significant low energy redistribution change in the CCD response. The top panel in Fig. 24 shows the evolution of PC grade 0 spectra of RX J1856.4-3754 between February 2005 and June 2007. Both spectra were obtained using time intervals when the source was not located on the bad columns. Fitting the spectra with the model described in
Fig. 14 gives a constant factor of
![]()
![]() 0.03 for February 2005 data and
0.03 for February 2005 data and
![]()
![]() 0.02 for June 2007 data. The use of a simple WABS*(BBODYRAD) with the column density fixed at 1.1
0.02 for June 2007 data. The use of a simple WABS*(BBODYRAD) with the column density fixed at 1.1 ![]() 1020 cm-2 gives a black-body temperature of kT=62.8
1020 cm-2 gives a black-body temperature of kT=62.8 ![]() 1.7 eV for both datasets; which is consistent with the canonical value found in the literature. A similar evolution is also observed in WT mode with a
constant factor of
1.7 eV for both datasets; which is consistent with the canonical value found in the literature. A similar evolution is also observed in WT mode with a
constant factor of
![]()
![]() 0.03 for February 2005 data and
0.03 for February 2005 data and
![]()
![]() 0.03 for June 2007 data. All the errors quoted above are given at
0.03 for June 2007 data. All the errors quoted above are given at
![]() .
Continuum spectra of Mkn 421 from March 2007 WT data also showed spectral fit residuals around the instrumental edges, especially the oxygen edge (see the bottom panel in Fig. 24), while no evidence for such residuals was observed in June 2006 data.
.
Continuum spectra of Mkn 421 from March 2007 WT data also showed spectral fit residuals around the instrumental edges, especially the oxygen edge (see the bottom panel in Fig. 24), while no evidence for such residuals was observed in June 2006 data.
All these changes are likely to be due to the build-up of charge traps over time. Charge traps are thought to be due to faults in the silicon crystalline structure which trap a fraction of the charge passing through them during the readout process. Therefore, only the events occurring above a trap in a given column experience a charge loss. The top panel in Fig. 25 gives an example of a charge trap formed just after launch in the column DETX 78. The operation of the CCD at relatively high temperatures (from -70 ![]() C to -50
C to -50 ![]() C) may partially fill the shallowest traps since the level of the thermally induced dark current is higher than that
expected at the designed operating temperature of -100
C) may partially fill the shallowest traps since the level of the thermally induced dark current is higher than that
expected at the designed operating temperature of -100 ![]() C (see Sect. 4.3).
C (see Sect. 4.3).
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi38.ps}\par\includegraphics[angle=-90,width=7cm,clip]{1157fi39.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg198.gif) |
Figure 24:
Effects of the build-up of charge traps on the XRT spectral response for continuum sources. ( Top panel) Evolution of the PC grade 0 spectrum of the soft neutron star RX J1856.4-3754 over time: (black) data from February 2005 and (red) data from June 2007. The decrease in the flux normalisation between the two epochs by |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=5cm,width=7cm,clip]{1157fi40.ps}\vspace*{5mm}
\includegraphics[width=7cm,clip]{1157fi41.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg199.gif) |
Figure 25:
( Top panel) PHA distribution of the Mn K |
| Open with DEXTER | |
Trap-induced line broadening is difficult to model since it may depend on the energy of the incident photons and the source intensity. Another uncertainty comes from the fact that the location and depth of the charge traps are unknown. Because all XRT spectral response files released so far have an incomplete modelling of the effect of CTI or traps, we urge caution in the interpretation of apparently sharp spectral features observed in XRT data from March 2007 onwards using the current calibration files.
Prospects to deal with the line broadening are under investigation:
Characterization of traps with the largest depth:
we are experimenting with a technique based on the characterization of the location and energy offset induced by charge traps with the largest depth. The bottom panel in Fig. 25 illustrates how powerful this technique can be in restoring the spectral resolution of the XRT; the Cas A Si line FWHM measured from corrected WT data from June 2007 is 109 eV compared to 131 eV before correcting the data (see Godet et al. 2007b).
Broadening of the RMF kernel:
we are developing a new tool which allows us to broaden the RMF kernel by convolving each of the 2400 RMF spectra with a flux-conserving function f with a CTI-dependent FWHM. All our experiments so far focused on WT mode, but the principle should be similar in PC mode. The line broadening is dominated by the effect of the deepest charge traps, which shift a given spectrum to lower energy by some amount. It is also important to take into account the fact that the amount of charge lost depends on energy in a subtle and poorly understood way.Since the true energy dependency is still unknown, we divided the 0.3-10 keV energy range into three ranges: 0.3-2 keV, 2-5 keV and 5-10 keV. Then, we defined in each of the three ranges an ad-hoc shape of the function f; i.e. in each range we assumed that the shift induced by a trap is constant and independent of the photon energy. The function f is defined as the sum of two Gaussians, with their width, relative normalisation and separation kept as free parameters to be optimised using data from celestial sources, so that the FWHM of each RMF monochromatic line photo-peak of the v011 WT RMFs, once convolved by f, is multiplied by a factor B which tracks the CTI increase over time.
To test this technique, we first calibrated the function f using March 2007 data, and we computed experimental WT RMFs with a broadened kernel. As illustrated in Fig. 26 (the top left panel), which shows the best fits of the March 2007 WT spectra of Mkn 421 (with an average count rate of 45 count s-1) using these RMFs along with the v011 WT ARFs, the residuals
around the instrumental edges are flattened when compared to Fig. 24 (bottom panel). We also investigated whether variation of the CCD temperature could have a significant impact on the trap properties, and so the line broadening. To do so, we considered four temperature ranges
with a width of 5 ![]() C from -70
C from -70 ![]() C to -52
C to -52 ![]() C using Mkn 421 data from March 2007 up to August 2007. We did not notice any significant change in the residuals around the instrumental edges when fitting the WT spectra using the experimental WT RMFs, even though the monitoring of the on-board corner sources has revealed a trend with temperature (a
C using Mkn 421 data from March 2007 up to August 2007. We did not notice any significant change in the residuals around the instrumental edges when fitting the WT spectra using the experimental WT RMFs, even though the monitoring of the on-board corner sources has revealed a trend with temperature (a ![]()
![]() increase in the FWHM at 5.9 keV from -70
increase in the FWHM at 5.9 keV from -70 ![]() C to -50
C to -50 ![]() C).
C).
We also tested these experimental WT RMFs on data from June 2007 up to September 2007 for other celestial sources with lower count rates, such as the SNR E0102-723 (1 count s-1) and the soft neutron star RX J1856.4-3754 (0.3 count s-1), to check the RMF kernel broadening and for any temporal evolution of the line broadening. Indeed, the higher the source count rate, the more likely the charge traps are to be filled; thus, it could be expected that brighter sources show a less significant broadening. However, since the XRT operates at much higher temperatures than it was designed for, most of the small charge traps should be already filled. Figure 26 shows the very good performance of these experimental WT RMFs. Specifically we see no intensity effect for sources between 0.3 count s-1 to 70 count s-1. Moreover, their use enables us to retrieve in the case of RX J1856.4-3754 (June 2007 data) a normalisation consistent with that found using 2005-2006 PC and WT data (see Sect. 3.3.1). This is because the new WT RMFs show a slight decrease of the QE at low energy to take into account the fraction of events lost below the on-board event threshold due to the effect of charge traps (see Fig. 27).
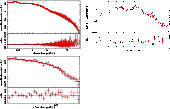 |
Figure 26:
WT spectra of celestial sources using the v011 WT ARFs and/or the experimental broadened WT RMFs: ( Top left panel) Fits of the Mkn 421 data from March 2007 using the experimental broadened WT RMFs. The WT grade 0 (black) and 0-2 (red) spectra contain more than 2 |
| Open with DEXTER | |
4.3 Increase of the substrate voltage to 6V
As discussed in Sect. 3.2.3, the XRT operates at higher than expected temperatures, resulting in significant thermally-induced noise appearing as low energy events. From experiments performed at the Leicester calibration facility on the Swift flight spare CCD-22 devices, we have demonstrated that raising the substrate voltage to
![]() V reduces the dark current, since the volume of silicon in which carriers are generated is reduced (Osborne et al. 2005; Godet et al. 2007b). Figure 28 clearly illustrates the benefit of raising the substrate voltage, since, for the same level of dark current, it is now possible to operate the CCD at a 3-4
V reduces the dark current, since the volume of silicon in which carriers are generated is reduced (Osborne et al. 2005; Godet et al. 2007b). Figure 28 clearly illustrates the benefit of raising the substrate voltage, since, for the same level of dark current, it is now possible to operate the CCD at a 3-4 ![]() C warmer temperature, and hence to collect useful science data up to -50
C warmer temperature, and hence to collect useful science data up to -50 ![]() C, before excessive hot pixels compromise the data. The only minor drawback of raising this voltage is that it induces a decrease of the depletion depth, and therefore of the QE at high energy and just below the Si edge (
C, before excessive hot pixels compromise the data. The only minor drawback of raising this voltage is that it induces a decrease of the depletion depth, and therefore of the QE at high energy and just below the Si edge (![]() 1.5-1.84 keV), due to the lower transparency of the silicon in
this energy range (see Fig. 4). The increase of the substrate voltage also results in a change in the gain C0, since the gain of the output FET is also modified in this new configuration.
1.5-1.84 keV), due to the lower transparency of the silicon in
this energy range (see Fig. 4). The increase of the substrate voltage also results in a change in the gain C0, since the gain of the output FET is also modified in this new configuration.
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi45.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg202.gif) |
Figure 27: WT grade 0-2 QE curves in the 0.2-1 keV energy band: (black) RMF v010, (red) RMF v011 and (green) broadened WT RMF v011. The loss of QE at low energy in the broadened WT RMF mimics the loss of events below the on-board central energy threshold due to the effect of charge traps. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=7cm,width=6cm,angle=-90,clip]{1157fi46.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg203.gif) |
Figure 28:
Evolution of the thermally induced dark current as a function of
the CCD temperature: (blue points) before the substrate voltage change to
|
| Open with DEXTER | |
Numerical simulations performed using our CCD response model and laboratory measurements made on a spare detector have shown that the QE decrease should be small (less than 10% at 6 keV; Osborne et al. 2005; Godet et al. 2007b). Short observations of two bright celestial targets with
![]() set to 6 V - Cas A (2.2 ks in PC mode and 0.8 ks in WT mode) and the Crab (0.6 ks in WT mode) - were also performed to estimate the on-board effective area change and to create new PC and WT gain files. The QE changes were measured to be
set to 6 V - Cas A (2.2 ks in PC mode and 0.8 ks in WT mode) and the Crab (0.6 ks in WT mode) - were also performed to estimate the on-board effective area change and to create new PC and WT gain files. The QE changes were measured to be ![]()
![]() at 6 keV and less than 10% in the 1.5-1.84 keV range. These
at 6 keV and less than 10% in the 1.5-1.84 keV range. These
![]() V gain files were released as version 007 prior to the
permanent change (see Table 2). The change in substrate voltage has made it necessary to release two sets of gain files, now distinguished by the characters ``s0'' and ``s6'' in their file names.
V gain files were released as version 007 prior to the
permanent change (see Table 2). The change in substrate voltage has made it necessary to release two sets of gain files, now distinguished by the characters ``s0'' and ``s6'' in their file names.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{1157fi47.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg204.gif) |
Figure 29:
Comparison of the residuals for PC grade 0-12 data of the SNR G21.5
collected at
|
| Open with DEXTER | |
Table 6: Best fit parameters of the PC grade 0-12 spectra extracted using the 40 arcsec core of the SNR G21.5.
Because the QE reduction was estimated to be rather small and the effect of the operational change on the spectroscopic performance was demonstrated not to be significant for most of the XRT observations (see Fig. 29 and Table 6), the substrate voltage was permanently raised to 6 V on-board on 2007 August 30.
Even though the QE change is small, and really noticeable only in WT spectra with more than 105 counts, the RMFs and ARFs need to be updated for both PC and WT modes. An intense phase of re-calibration of the instrument is ongoing, as indicated in Table 1. The full details of the calibration of the
![]() V response files will be addressed in a forthcoming paper. By the time this paper is published, new response matrices will be available that
take the QE change into effect properly.
V response files will be addressed in a forthcoming paper. By the time this paper is published, new response matrices will be available that
take the QE change into effect properly.
5 Conclusion
We described in detail our Monte-Carlo simulation, computing the Swift-XRT PC and WT RMFs. The response model is mainly based on a physical description of the interaction of photons in the CCD. We showed how we used in-flight calibration to improve the XRT spectral response (the low-energy
response, the line profile and the shelf) by implementing empirical corrections when it was not possible to implement physical ones. All the changes allow us to describe the CCD response well. We showed that the v011 XRT response files, calibrated using data collected at
![]() V, give
good performance on continuum and line sources in both PC and WT mode when compared to other X-ray instruments in the 0.3-10 keV energy band (the recommended bandpass) with a systematic error of less than 3% in both modes over 0.3-10 keV and better than 10% in absolute flux.
V, give
good performance on continuum and line sources in both PC and WT mode when compared to other X-ray instruments in the 0.3-10 keV energy band (the recommended bandpass) with a systematic error of less than 3% in both modes over 0.3-10 keV and better than 10% in absolute flux.
We also showed that the XRT spectral response calibration was complicated by various effects, such as energy offsets, related to the way the CCD is operated in orbit. We described how these effects can be corrected in the ground processing software thanks to the task XRTWTCORR in WT mode and the task XRTPCBIAS in PC mode, and the release of temperature-dependent gain files. We stressed that the CCD started showing evidence of degradation of its spectroscopic performance (line broadening, small residuals around the instrumental edges and change in the low-energy response) when fitting spectra of celestial sources from the middle of 2007. This is due to the build-up of charge traps in the CCD, produced by high-energy proton and radiation damage. We are developing RMFs with a broadened kernel, enabling us to handle the line broadening over time. The preliminary results in WT mode are promising. Before the release of broadened kernel RMFs in either mode, we recommend that users should be cautious in any interpretation of the data.
In order to improve further the XRT spectral performance, the substrate voltage was raised permanently to
![]() V on-board on 2007 August 30. This change resulted in a slight decrease of the QE at high energy (E > 3 keV) and just below the Si edge (1.0-1.8 keV). This QE change is really only noticeable when fitting high statistical quality spectra with more than
105 counts. An intense phase of re-calibration of the instrument is on-going to update the spectral response files. In the meantime, we recommend the use of the v011 response files, and we advice the user to be cautious in the spectral analysis of XRT data until the response files are updated.
V on-board on 2007 August 30. This change resulted in a slight decrease of the QE at high energy (E > 3 keV) and just below the Si edge (1.0-1.8 keV). This QE change is really only noticeable when fitting high statistical quality spectra with more than
105 counts. An intense phase of re-calibration of the instrument is on-going to update the spectral response files. In the meantime, we recommend the use of the v011 response files, and we advice the user to be cautious in the spectral analysis of XRT data until the response files are updated.
Acknowledgements
O.G., A.P.B., J.P.O., A.F.A., K.L.P. gratefully acknowledge STFC funding. This work is supported at INAF by funding from ASI through grant I/011/07/0.
References
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [NASA ADS] [CrossRef] (In the text)
- Beardmore, A. P., et al. 2007, Swift XRT calibration note - energy scale offsets, http://swift.gsfc.nasa.gov/docs/heasarc/caldb/swift/docs/xrt/xrt_bias.pdf] (In the text)
- Beuermann, K., Burwitz, V., & Rauch, T. 2006, A&A, 458, 541 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bode, M. F., O'Brien, T. J., Osborne, J. P., et al. 2006, ApJ, 652, 629 [NASA ADS] [CrossRef] (In the text)
- Brocksopp, C., et al. 2005, MNRAS, 365, 1203 [NASA ADS] (In the text)
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] (In the text)
- Burrows, D. N., Falcone, A., Chincarini, G., et al. 2007, Phil. Trans. Roy. Soc. Lond. A, 365, 1213 [NASA ADS] [CrossRef] (In the text)
- Butler, N. 2007, ApJ, 656, 1001 [NASA ADS] [CrossRef] (In the text)
- Campana, S., Mangano, V., Blustin, A. J., et al. 2006, Nature, 442, 1008 [NASA ADS] [CrossRef] (In the text)
- Campana, S., Lazzati, D., Ripamonti, E., et al. 2007, ApJ, 654, 17 [NASA ADS] [CrossRef] (In the text)
- Campana, S., Panagia, N., Lazzati, D., et al. 2008a, ApJ, 683, 9 [NASA ADS] [CrossRef] (In the text)
- Campana, S., et al. 2008b, in preparation (In the text)
- Capalbi, M., et al. 2005, Swift XRT data reduction guide, http://swift.gsfc.nasa.gov/docs/analysis/xrt_swguide_v1_2.pdf (In the text)
- Carpenter, J. D., Abbey, A. F., Ambrosi, R. M., & Wells, A. 2006, Proc. SPIE, 6266, 62663K (In the text)
- Chincarini, G., Moretti, A., Romano, P., et al. 2007, ApJ, 671, 1903 [NASA ADS] [CrossRef] (In the text)
- Esposito, P., Caraveo, P. A., Pellizzoni, A., et al. 2007, A&A, 474, 575 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Falcone, A. D., Burrows, D. N., Lazzati, D., et al. 2006, ApJ, 641, 1010 [NASA ADS] [CrossRef] (In the text)
- Falcone, A. D., Morris, D., Racusin, J., et al. 2007, ApJ, 671, 1921 [NASA ADS] [CrossRef] (In the text)
- Fitting, H. J., Glaefeke, H., & Wild, W. 1977, Phys. Stat. Sol., 43, 185 [CrossRef] (In the text)
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] (In the text)
- Goad, M. R., Page, K. L., Godet, O., et al. 2007, A&A, 468, 103 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Godet, O., Page, K. L., Osborne, J. P., et al. 2006, A&A, 452, 819 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Godet, O., Page, K. L., Osborne, J., et al. 2007a, A&A, 471, 385 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Godet, O., Beardmore, A. P., Abbey, A. F., et al. 2007b, Proc. SPIE, 6686, 66860A (In the text)
- Godet, O., et al. 2008, Swift XRT release note for v011 response files, http://swift.gsfc.nasa.gov/docs/heasarc/caldb/swift/docs/xrt/SWIFT-XRT-CALDB-09_v11.pdf (In the text)
- Hachisu, I., Kato, M., & Luna, G. J. M. 2007, ApJ, 659, 153 [NASA ADS] [CrossRef] (In the text)
- Hill, J. E., Burrows, D. N., Nousek, J. A., et al. 2004, Proc. SPIE, 5165, 217 (In the text)
- Hill, J. E., Angelini, L., Morris, D. C., et al. 2005, Proc. SPIE, 5898, 313 [NASA ADS] (In the text)
- Hopkinson, G. R. 1983, NIMA, 216, 423 [NASA ADS] [CrossRef] (In the text)
- Janesick, J., et al. 1985, Proc. SPIE, 597, 364 [NASA ADS] (In the text)
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Keay, A., Owens, A., Gurman, S. J., et al. 1995, NIMB, 97, 316 [NASA ADS] [CrossRef] (In the text)
- Kennea, J. A., Burrows, D. N., Pagani, C., et al. 2007, Proc. SPIE, 6686, 668608 (In the text)
- McCarthy, K. J., Owens, A., Holland, A. D., & Wells, A. A. 1995, NIMA, 362, 538 [NASA ADS] [CrossRef] (In the text)
- Molina, M., Giroletti, M., Malizia, A., et al. 2007, MNRAS, 382, 937 [NASA ADS] [CrossRef] (In the text)
- Moretti, A., Margutti, R., Pasotti, F., et al. 2008a, A&A, 478, 409 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Moretti, A., et al. 2008b, A&A, accepted (In the text)
- Mukerjee, K., Osborne, J. P., Wells, A. A., et al. 2004, Proc. SPIE, 5165, 251 (In the text)
- Nousek, J. A., Kouveliotou, C., Grupe, D., et al. 2006, ApJ, 642, 389 [NASA ADS] [CrossRef] (In the text)
- O'Brien, P. T., Willingale, R., Osborne, J., et al. 2006, ApJ, 647, 1213 [NASA ADS] [CrossRef] (In the text)
- Osborne, J. P., Beardmore, A. P., Godet, O., et al. 2005, Proc. SPIE, 5898, 352 [NASA ADS] (In the text)
- Owens, A., Fraser, G. W., Abbey, A. F., et al. 1996a, NIMA, 382, 503 [NASA ADS] [CrossRef] (In the text)
- Pagani, C., & Morris, D. 2008, Swift XRT release note for v008 gain files, http://swift.gsfc.nasa.gov/docs/heasarc/caldb/swift/docs/xrt/SWIFT-XRT-CALDB-04_v8.pdf
- Pavlov, G. G., & Nousek, J. A. 1999, NIMA, 439, 348 [NASA ADS] (In the text)
- Popp, M., Hartmann, R., Soltau, H., et al. 2000, NIMA, 439, 567 [NASA ADS] [CrossRef] (In the text)
- Plucinsky, P. P., Haberl, F., Dewey, D., et al. 2008, Proc. SPIE, 7011 [arXiv:0807.2176] (In the text)
- Romano, P., Sidoli, L., Mangano, V., Mereghetti, S., & Cusumano, G. 2007, A&A, 469, 5 [NASA ADS] [CrossRef] (In the text)
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] (In the text)
- Rykoff, E. S., Miller, J. M., Steeghs, D., & Torres, M. A. P. 2007, ApJ, 666, 1129 [NASA ADS] [CrossRef] (In the text)
- Short, A. D., Ambrosi, R. M., & Turner, M. J. L. 2002, NIMA, 484, 211 [NASA ADS] [CrossRef] (In the text)
- Tramacere, A., Giommi, P., Massaro, E., et al. 2007, A&A, 467, 501 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tueller, J., Mushotzky, R. F., Barthelmy, S., et al. 2008, ApJ, 681, 113 [NASA ADS] [CrossRef] (In the text)
- Wijnands, R., et al. 2007, MNRAS, in press [arXiv:0709.0061] (In the text)
- Willingale, R., O'Brien, P. T., Cowley, S. W. H., et al. 2006, ApJ, 649, 541 [NASA ADS] [CrossRef] (In the text)
- Willingale, R., O'Brien, P. T., Osborne, J. P., et al. 2007, ApJ, 662, 1093 [NASA ADS] [CrossRef] (In the text)
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef]
- Zhang, B., Fan, Y. Z., Dyks, J., et al. 2006, ApJ, 642, 354 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...%
![[*]](/icons/foot_motif.gif)
- See http://swift.gsfc.nasa.gov/docs/swift/archive/grb_table/grb_stats.php
- ... package
![[*]](/icons/foot_motif.gif)
- http://swift.gsfc.nasa.gov/docs/swift/analysis/xrt_swguide_v1_2.pdf
- ... (80 DN
![[*]](/icons/foot_motif.gif)
- Digital number.
- ... observation
![[*]](/icons/foot_motif.gif)
- http://swift.gsfc.nasa.gov/docs/heasarc/caldb/swift/docs/xrt/SWIFT-XRT-CALDB-04_v2.pdf
All Tables
Table 1: Summary of the in-flight calibration targets used since the launch on 2004 November 20.
Table 2: Summary of the releases of the XRT post-launch gain files.
Table 3: Summary of the releases of the XRT post-launch RMFs.
Table 4: Summary of the spectral parameters obtained when fitting Swift-XRT, XMM-Newton, Chandra and RXTE data for several continuum sources.
Table 5: The second part of Table 4.
Table 6: Best fit parameters of the PC grade 0-12 spectra extracted using the 40 arcsec core of the SNR G21.5.
All Figures
![\begin{figure}
\par\includegraphics[height=5.5cm,width=8.cm,clip]{1157fig1.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg38.gif) |
Figure 1:
Energy resolution (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{1157fig2.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg44.gif) |
Figure 2:
Architecture of the CCD response model used to compute the XRT RMFs. The RMFs contain 2400 input energy channels with a 5 eV energy width. In each energy channel,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=12cm,width=14.cm,clip]{1157fig3.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg47.gif) |
Figure 3:
Pictures of the CCD-22 structure and geometry of a CCD-22 pixel as used in our spectral response code. ( Top left and right panels) Top and side view of a CCD-22 pixel, respectively. These images were obtained by a scanning electron microscope provided by e2v. The different parts of the pixel are shown on these two images. ( Bottom left and right
panels) Geometry of the CCD-22 pixel as used in our CCD response model (the dimensions are given in units of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1157fig4.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg66.gif) |
Figure 4: Linear absorption coefficients of the CCD-22 compounds: (solid line) Si; (dotted line) SiO2; (dashed line) Si3N4. The small inset shows the XAFS just above the Si edge. The energy of the Si edge is slightly different depending on the compound considered. This is due to differences in the crystal lattice structure. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=16cm,width=16cm,clip]{1157fig5.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg77.gif) |
Figure 5:
List of the XRT event grades: ( left) for PC mode, a 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{1157fig6.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg85.gif) |
Figure 6:
Spectra from the Mn K |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1157fig7.ps}\par\includegraphics[angle=-90,width=7cm,clip]{1157fig8.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg88.gif) |
Figure 7:
( Top panel) PC grade 0 spectrum measured at the Leicester
calibration facility from the Si K |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1157fig9.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg89.gif) |
Figure 8: CCD-22 simplified schematic diagram. The four 55Fe corner sources permanently illuminating areas of the CCD outside the field of view are shown as grey circles. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{1cm}\includegraphics[width=6cm,clip]{1157fi10.ps}\hspace*{1cm}}
\par\includegraphics[width=8cm,clip]{1157fi11.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg93.gif) |
Figure 9: ( Top panel) Detector coordinate image showing the SNR Cas A when scattered optical light from the sunlit Earth is present on the detector (visible on the left side of the detector). ( Bottom panel) PC mode light-curve of the SNR Cas A in the 0.3-10 keV energy range for different snapshots and grade selections: 0, 1-4, 5-12 and 13-31. The light-curve was obtained before bias correction. The drop of the count rate in the PC grade 0 light-curve is due to the presence of scattered optical light from the sunlit Earth, which induces a grade migration from good grades (0-12) to higher grades. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=6cm,width=7cm,clip]{1157fi12.ps}\par\includegraphics[height=6cm,width=7cm,clip]{1157fi13.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg94.gif) |
Figure 10: ( Top panel) Comparison of the event energy spectra of the Si and S lines in the North (N) and South East (SE) knots of the SNR Cas A as observed by the XMM-Newton MOS cameras (N: black; SE: red) and the Swift-XRT (N: green, cyan; SE: blue, magenta). The green and blue crosses correspond to XRT/PC grade 0 data for which the bias was contaminated by optical light from the sunlit Earth. The data were processed with the v2.6 XRT software which does not correct for bias contamination. In this case, an energy scale offset is observed when compared with the XMM-Newton MOS spectra. The cyan and magenta crosses correspond to the same data processed with the XRT software including the task XRTPCBIAS, which corrects the data. ( Bottom panel) Swift-XRT WT grade 0-2 spectrum of RS Ophiuchi: (black) the data not corrected for the bias contamination and (red and blue) the data corrected using the modified task XRTWTCORR. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi14.ps}\par\includegraphics[angle=-90,width=7cm,clip]{1157fi15.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg95.gif) |
Figure 11:
( Top panel) WT grade 0-2 spectrum of the SNR Cas A in the energy band of the Si K |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1157fi16.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg96.gif) |
Figure 12:
( Top panel) Evolution of the gain C0 at a CCD temperature of -65 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1157fi17.ps}\vspace*{5mm}
\includegraphics[angle=-90,width=7.5cm,clip]{1157fi18.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg106.gif) |
Figure 13:
Spectra of the entire SNR Cas A in WT mode at different epochs:
(black) 2005-02-16; (red) 2006-04-20; (green) 2007-06-06. The blue line indicates the expected energy centroid of the Si and S K |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi19.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg114.gif) |
Figure 14: Comparison of the low-energy response between v007 (black) and v008 (red) RMFs using the spectrum of the soft neutron star RX J1856.4-3754 in PC mode for grade 0 events. We used a CONST*WABS*(BBODYRAD+BBODYRAD) model with the spectral parameters fixed to the values given in Beuermann et al. (2006). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=7cm,clip]{1157fi20.ps}...
...ce*{3mm}
\includegraphics[angle=-90,width=7cm,clip]{1157fi23.ps} }\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg115.gif) |
Figure 15:
Best fits of absorbed sources (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=6.8cm,clip]{1157fi24.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg118.gif) |
Figure 16: Plot of the PC quantum efficiency using v007 RMF for: grade 0-12 (red) and grade 0 (black). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1157fi25.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg120.gif) |
Figure 17: PC grade 0-12 spectrum of the 55Fe source on the XRT camera door fitted using the v009 RMF. The low energy shoulders of the lines are now correctly modelled using the Pavlov & Nousek formalism (compare to Fig. 7 lower panel). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi26.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg121.gif) |
Figure 18:
WT grade 0-2 spectrum of Mkn 421 from June 2006 data fitted using the v010 (black) and v011 (red) RMFs. The residuals around 0.9-1.0 keV (black points) are due to a RMF redistribution issue in v007-v010 WT RMFs. The use of the new v011 WT RMFs including a slight change in the loss function between 1 and 2 keV gives flatter residuals in this region (red
points). The spectral model is an absorbed bending power-law with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi27.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg122.gif) |
Figure 19:
Gaussian models with a value of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi28.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg123.gif) |
Figure 20:
Best fits of the WT grade 0 spectrum of Mkn 421 using the WT grade 0 v011 RMF together with the theoretical ARF (black) and the new ARF v011 (red) which includes the correction of the CCD QE just above the Si K |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{5mm}\includegraphics[width=6cm,clip]{1157fi29.ps}\...
...*{5mm}}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi30.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg124.gif) |
Figure 21:
( Top panel) Drawing showing the changes in the geometry of the
finger and channel stop, corresponding to a reduction of the open area by |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1157fi31.ps}\par\includegraphics[width=7cm,clip]{1157fi32.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg126.gif) |
Figure 22:
( Top panel) Comparison of the XRT total effective area (EA) in PC and WT mode using the v011 response files. The PC grade 0 EA is very low when compared to the PC grade 0-12 and WT EA even at low energy (E < 1 keV) where we expect to have a similar QE level whatever the mode and grade selection. Below |
| Open with DEXTER | |
| In the text | |
 |
Figure 23:
Plots showing the best fits to different celestial sources when using the v011 PC and WT response files. a) WT grade 0 (black) and grade 0-2 (red) spectra of the blazar Mkn 421 observed in June 2006. The spectral model is an absorbed bending power-law (i.e. WABS * exp[- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi38.ps}\par\includegraphics[angle=-90,width=7cm,clip]{1157fi39.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg198.gif) |
Figure 24:
Effects of the build-up of charge traps on the XRT spectral response for continuum sources. ( Top panel) Evolution of the PC grade 0 spectrum of the soft neutron star RX J1856.4-3754 over time: (black) data from February 2005 and (red) data from June 2007. The decrease in the flux normalisation between the two epochs by |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=5cm,width=7cm,clip]{1157fi40.ps}\vspace*{5mm}
\includegraphics[width=7cm,clip]{1157fi41.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg199.gif) |
Figure 25:
( Top panel) PHA distribution of the Mn K |
| Open with DEXTER | |
| In the text | |
 |
Figure 26:
WT spectra of celestial sources using the v011 WT ARFs and/or the experimental broadened WT RMFs: ( Top left panel) Fits of the Mkn 421 data from March 2007 using the experimental broadened WT RMFs. The WT grade 0 (black) and 0-2 (red) spectra contain more than 2 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{1157fi45.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg202.gif) |
Figure 27: WT grade 0-2 QE curves in the 0.2-1 keV energy band: (black) RMF v010, (red) RMF v011 and (green) broadened WT RMF v011. The loss of QE at low energy in the broadened WT RMF mimics the loss of events below the on-board central energy threshold due to the effect of charge traps. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=7cm,width=6cm,angle=-90,clip]{1157fi46.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg203.gif) |
Figure 28:
Evolution of the thermally induced dark current as a function of
the CCD temperature: (blue points) before the substrate voltage change to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{1157fi47.ps}
\end{figure}](/articles/aa/full_html/2009/05/aa11157-08/Timg204.gif) |
Figure 29:
Comparison of the residuals for PC grade 0-12 data of the SNR G21.5
collected at
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.