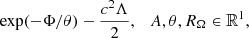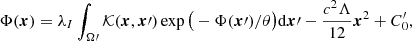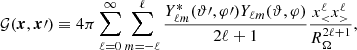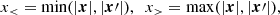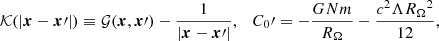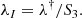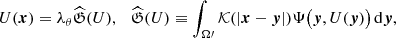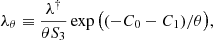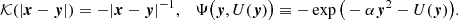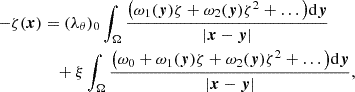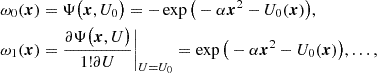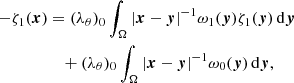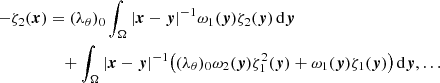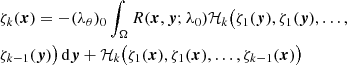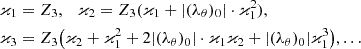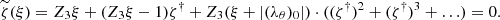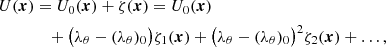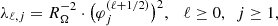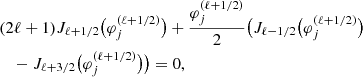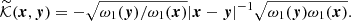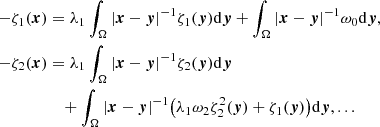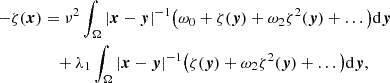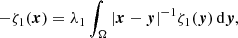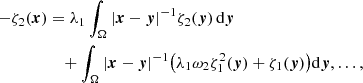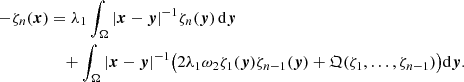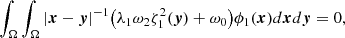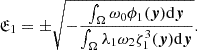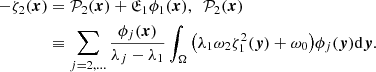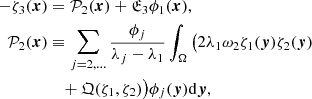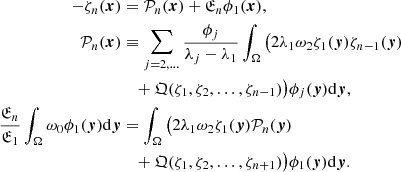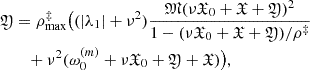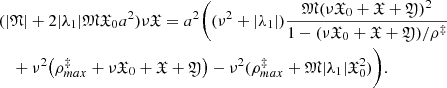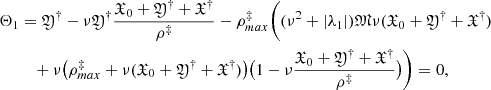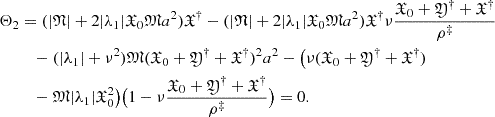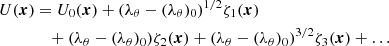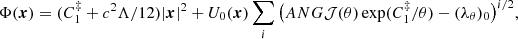| Issue |
A&A
Volume 694, February 2025
|
|
|---|---|---|
| Article Number | A252 | |
| Number of page(s) | 7 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202553679 | |
| Published online | 20 February 2025 | |
Cosmic voids and the kinetic analysis
IV. Hubble tension and the cosmological constant
1
Center for Cosmology and Astrophysics, Alikhanian National Laboratory, Alikhanian Brothers str.2, 0036, and Yerevan State University, Manukian str.1, 0025 Yerevan, Armenia
2
SIA, Sapienza Università di Roma, Via Salaria 851/881, 00191 Rome, Italy
3
Keldysh Institute of Applied Mathematics of RAS, Miusskaya Sq. 4, 125047 Moscow, Russia
4
Institute of Computer Aided Design of RAS, 2nd Brestskaya st., 123056 Moscow, Russia
⋆ Corresponding author; gurzadyan@yerphi.am
Received:
4
January
2025
Accepted:
13
January
2025
The formation of cosmic structures in the late Universe was considered using the Vlasov kinetic approach. The crucial point is the use of the gravitational potential with repulsive term of the cosmological constant, which provides a solution to the Hubble tension, that is, the Hubble parameter for the late Universe has to differ from its global cosmological value. This also provides a mechanism of formation of stationary semi-periodic gravitating structures of voids and walls, so that the cosmological constant has the role of the scaling. It can therefore be compared with the observational data for given regions. The considered mechanism of the structure formation in the late cosmological epoch then succeeds the epoch described by the evolution of primordial density fluctuations.
Key words: large-scale structure of Universe
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Hubble tension (Riess 2020; Riess et al. 2024a,b; Di Valentino et al. 2021; Dainotti et al. 2023; Scolnic et al. 2024a,b) has attracted attention to the possibly genuine differences in the descriptions of the late and early Universe, including of the structure formation and the large-scale flows (e.g. Capozziello & Lambiase 2022; Bouchè et al. 2022; Bajardi et al. 2022; Capozziello & D’Agostino 2023). The problems of the nature of dark matter and dark energy are still unsolved, and diverse approaches and models are developed to consider the entire scope of the observational challenges (see Capozziello et al. 2024; de Pedreira 2024 and references therein).
The evolution of primordial density fluctuations as the origin of the cosmic structure formation (Peebles 1993) at large scales is described by the hydrodynamical pancake theory of Zeldovich (Zeldovich 1970; Shandarin 1989). It predicts the formation of the cosmic web and the filaments. At smaller scales, scales of clusters and groups of galaxies, the role of local gravitational interaction dominates. Namely, while the hydrodynamic approach assumes little influence of the intrinsic gravity of the involved particles as compared to the influence on the geometry of inhomogeneities 2D caustics; Arnold et al. 1982; Arnold 1982) of the Friedmann flow, the kinetic field approach is assumed to be suitable for relatively fast non-equilibrium phenomena in an external quasi-ordered medium, when the wave fronts overturn and in the intersection of three-dimensional matter flows channels for kinetic processes are formed (Gurzadyan et al. 2022, 2023a,b).
The possible tension of the late (local) and early (global) Universe outlines these differences in the mechanisms of structure formation and of the flows at large and small scales. Namely, the explanation of the Hubble tension as a result of two flows, a local and a global flow, with a non-identical Hubble constant, was provided in Gurzadyan & Stepanian (2021a,b) based on the theorem proved in Gurzadyan (1985). This theorem states the general function that fulfils the equivalency of gravity of a sphere and of a point mass in the following form for the force
This function ensures a non-force-free gravitational field inside a shell, and the second term in the left-hand side involves the cosmological constant in weak-field General Relativity and McCrea-Milne non-relativistic cosmological model (McCrea & Milne 1934; Zeldovich 1981). Importantly, Gurzadyan & Stepanian (2018), Gurzadyan (2019), Gurzadyan & Stepanian (2019, 2020) showed that Eq. (1) enables us to describe the observational data of the dynamics of groups and clusters of galaxies. Moreover, observational data support the non-force-free field inside a shell, as predicted by Eq. (1), that is, the influence of the galactic haloes on the properties of the spiral galaxies (Kravtsov 2013).
Then, the late Hubble flow is described by the equation (Gurzadyan & Stepanian 2021a,b)
where H0 is the local Hubble parameter, and ρ0 is the local mean density of matter. This equation follows from Eq. (1) and has the structure of the standard Friedmann equation, but it has a different content within the non-relativistic McCrea-Milne model with a cosmological constant.
Below, we continue the Vlasov kinetic analysis (Gurzadyan et al. 2022, 2023a,b) of the structure formation in the small-scale Universe. The essential point in the analysis is the role of the cosmological constant, and hence, that the evolutionary paths of the filament formation are the result of the self-consistent gravitational interaction of the particles along with the repulsive cosmological term. Namely, it appears that zones with a dominating influence of the ascending and descending branches of the modified gravitational potential of Eq. (1) form a topologically different multi-connected matter structure in the Universe. We analysed the of quasi-static processes that occurred in the system defined by the Vlasov-Poisson equations near its state of relative equilibrium. In this case, as shown, it is reasonable to reduce the problem to the analysis of the integral equation of a Hammerstein type. For the latter, the corresponding boundary problem is again based on the theorem in Gurzadyan (1985) because the structure of the of solutions of this integral equation and of the possible singularities can be expressed using known formalisable representations. We investigated the properties of the spectrum of the non-linear integral operator and its relation to the spectrum of the Fredholm operator for the linear potential, which enabled us to reveal the deterministic way of the formation of coherent filaments in local regions in the Universe.
2. The kinetic approach
The starting point for obtaining hydrodynamic models with singularities, that is, caustics and kinetic models without taking into account the influence of gravity, is the introduction of the Friedmann flow. This is characterized by a field of velocities whose values for each pair of points in space are proportional to the distance between these points, v = HΔr. The Friedmann flow in these models was considered as some analogue of an equilibrium state, which is perturbed either by inhomogeneity in the initial data set or by random fluctuations in the density that lead to the formation of a geometrical small inhomogeneity (adiabatically stable) of the spatial distribution of particles of the system on the background of this flow. The smallness is caused by random deviations, which are assumed a priori to be essentially limited in norm in comparison with the basis values of the mean parameters.
The system of Vlasov–Poisson equations for describing of dynamics in a system of N cosmological objects (with masses mi = 1, …, N = m ≡ 1) may be represented as (see Gurzadyan et al. 2022 for details)
where F(x, v, t) is the distribution function of gravitationally interacting particles, A is the normalization factor for the particle density, t0 is a fixed moment in time, and G is the gravitational constant. The system of objects or particles is considered within the finite domain of configurational space 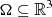 (diam Ω ≤ ∞), with a C2-smooth boundary ∂Ω.
(diam Ω ≤ ∞), with a C2-smooth boundary ∂Ω.
Equation (4) is the non-linear Poisson equation, which accounts for the cosmological term of Eq. (3). The third term on the right-hand side of the kinetic Equation (3) may be represented as
where 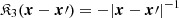 ,
, 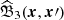 is an operator term that takes into account the influence of the boundary conditions. The classical Newtonian potential ΦN(r) = − Gm/r increases monotonically in the interval r ∈ (0, +∞) (ΦN ∈ ( − ∞, 0)), while the generalised (with cosmological term) Newton gravity potential
is an operator term that takes into account the influence of the boundary conditions. The classical Newtonian potential ΦN(r) = − Gm/r increases monotonically in the interval r ∈ (0, +∞) (ΦN ∈ ( − ∞, 0)), while the generalised (with cosmological term) Newton gravity potential
has a maximum
where rc = (Gm/(3Λc2))1/3 (it increases in the interval r ∈ (0; rc] and decreases in the interval r ∈ (rc; ∞)).
We consider the stationary case of dynamics, F = F(x, v). However, the further analysis mainly concerns the second equation of the system, which is the Poisson equation relative to the potential, and no explicit time dependence is observed in it. When it varies, the Hilbert–Einstein–Maxwell action (Vedenyapin et al. 2021) can therefore be a separate variation over the fields (for a fixed particle distribution) and a variation over the distribution functions (with fixed fields). The approach we considered is therefore applicable for adiabatic processes at a quasi-equilibrium (weakly varying) particle distribution functions. In this case, we can use the energy substitution for a unique variable of the distribution function Vedenyapin et al. (2011): 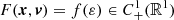 , where ε = mv2/2 + Φ(x). Thus, the particle density in the right side of the Poisson equation can be expressed in terms of the equilibrium solution of the Vlasov equations. This solution is identical to Maxwell–Boltzmann distributions f = f0(ε) = ANexp(−ε/θ). However, the physical meaning of the equilibrium solution of the Vlasov equation is essentially different from that of the Boltzmann equation. This solution must meet the following requirements: (1)a maximum possible statistical independence, (2)an isotropy of the velocity distribution, and (3)stationarity of the distribution in the form
, where ε = mv2/2 + Φ(x). Thus, the particle density in the right side of the Poisson equation can be expressed in terms of the equilibrium solution of the Vlasov equations. This solution is identical to Maxwell–Boltzmann distributions f = f0(ε) = ANexp(−ε/θ). However, the physical meaning of the equilibrium solution of the Vlasov equation is essentially different from that of the Boltzmann equation. This solution must meet the following requirements: (1)a maximum possible statistical independence, (2)an isotropy of the velocity distribution, and (3)stationarity of the distribution in the form 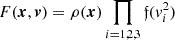 . The substitution expression into the Vlasov equation gives
. The substitution expression into the Vlasov equation gives
and we obtain a system of ODEs,
where θ is a constant of separation of variables, and its physical meaning is kinetic temperature in the system of interacting collisionless particles (in accordance with Vlasov’s definition (Vlasov 1961, 1978), thermodynamic/collisional equilibrium is globally absent in this system).
Equation (4) for the gravitational potential can be written as
where RΩ is the radius of the region Ω and is accepted in the form of a ball in configurational 3–space (as the simplest physically realizable case).
The Poisson equation (4) takes the form of the inhomogeneous equation of Liouville–Gelfand (LG; Dupaigne 2011), in which the local (generalized) temperature changes sign depending on the value of the derivative of the potential at a given point: As mentioned above, for the two-particle problem (in particular, for a formal pair in the form of a centre coalescence of the main part of the particles and the conditional extremely distant particle) the repulsive force can dominate due to the presence of a quadratic term ∼|x|2. Generalised to the indefinite thermodynamics of a system of gravitating particles, this becomes similar to that for the Onsager vortices in classical hydrodynamics (Fimin & Chechetkin 2020), and the existence of solutions of the LG equation for large system sizes ensures the existence of solutions to the Vlasov Equation (3). This can be shown using the parametric Young inequality (Pokhozhaev 2010). It was shown (Gurzadyan et al. 2022) that for the conditions c2Λ ≷ 3πλ† (θ ≷ 0), the system of Vlasov–Poisson equations has solutions of the type of distribution functions that admit the energy substitution, and the potential of the gravitational field, which has the property of convexity (in the general case, for an arbitrary RΩ ≤ ∞, in contrast to the case of the attraction potential, for which there is a limit RΩ < (C0θ2/(λ†/S32)2)1/4). We used the notation 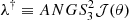 ,
, 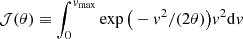 .
.
As already noted in Gurzadyan et al. (2022), in the formulation of the Dirichlet problem for the Poisson Equation (4) (or (8)) with a constant right-hand side on the boundary of the Ω region according to a McCrea-Milne averaging gravitational field outside the compact subdomain Ω0 that contains a system of particles (that is situated in the region Ω (meas Ω0 ≪ meas Ω)), we can assume the boundary condition on the ∂Ω as given in accordance with the theorem in Gurzadyan (1985).
The solution of the Dirichlet problem may be obtained with the help of an integral representation of the equation for a gravitational (double–layer) potential (Nowakowski 2001). The equation for the potential with a Maxwell–Boltzmann particle density, corresponding to an internal Dirichlet problem in a bounded domain Ω (under boundary conditions corresponding to the Milne–McCrea model) has the following form:
In essence, the above is the explicit form of the equation for the potential introduced in expression (5), where the Green function 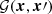 for the inner boundary value problem in the domain Ω (in this case, due to symmetry of the latter, we have
for the inner boundary value problem in the domain Ω (in this case, due to symmetry of the latter, we have 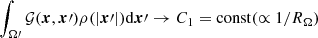 ). We introduce a new variable U(x)≡(Φ(x)−C0′−C1)/θ + α|x|2, α ≡ c2Λ/(12θ), and the above equation can be written as the uniform Hammerstein integral equation,
). We introduce a new variable U(x)≡(Φ(x)−C0′−C1)/θ + α|x|2, α ≡ c2Λ/(12θ), and the above equation can be written as the uniform Hammerstein integral equation,
For θ > 0, we obtain λθ > 0, the mapping 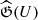 is a compact (in L2(Ω)) non-linear operator, since the conditions of the Nemytskij–Vainberg theorem (Krasnosel’sky 1964) are satisfied for it, (
is a compact (in L2(Ω)) non-linear operator, since the conditions of the Nemytskij–Vainberg theorem (Krasnosel’sky 1964) are satisfied for it, (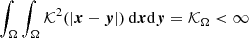 ,
, 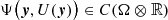 and |Ψ(y, U(y))|≤g(y)+CΨ ⋅ |U|, g ∈ L2(Ω), g(y),CΨ > 0).
and |Ψ(y, U(y))|≤g(y)+CΨ ⋅ |U|, g ∈ L2(Ω), g(y),CΨ > 0).
In the expression Ψ† ≡ ∫0UΨ(y, U)dU = exp(−αy2)⋅(exp(−U)−1) it is clear that Ψ† ≤ τ1|U|+τ2 (x ∈ Ω), where τ1, 2 > 0, τ1 < 1/λ𝒦, λ𝒦 is the maximum eigenvalue of the integral equation kernel 𝒦. Then, in accordance with theorem 2.8 in Zabreiko et al. (1975), the Hammerstein equation has at least one solution U0(x). We consider the question of the uniqueness of a solution or the presence of many solutions in the next paragraph.
3. Solutions and cosmological consequences
We assumed that for λ = (λθ)0 Eq. (10) has a non-trivial solution U = U0. We considered the Fredholm determinant 𝒟(λ) (Zemyan 2012) for an integral kernel of the linearised (in the vicinity O(U0) of the basic solution U0) Hammerstein equation 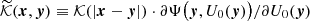 . After linearisation (an application of the Frechet derivative), we obtained the linear Fredholm self-adjoint compact operator with a discrete spectrum (on the real axis; Krasnosel’sky 1964). If
. After linearisation (an application of the Frechet derivative), we obtained the linear Fredholm self-adjoint compact operator with a discrete spectrum (on the real axis; Krasnosel’sky 1964). If 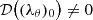 (i. e. (λθ)0 is not the characteristic value of the kernel
(i. e. (λθ)0 is not the characteristic value of the kernel 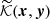 ), then in the vicinity O((λθ)0) Eq. (10) has a unique analytic (by powers of (λθ − (λθ)0)j, j = 1, 2, …) solution U(x|λθ) (Corduneanu 1991), for which limλθ → (λθ)0U(x|λθ) = U0(x) (∀x ∈ Ω).
), then in the vicinity O((λθ)0) Eq. (10) has a unique analytic (by powers of (λθ − (λθ)0)j, j = 1, 2, …) solution U(x|λθ) (Corduneanu 1991), for which limλθ → (λθ)0U(x|λθ) = U0(x) (∀x ∈ Ω).
We considered the solution of (10) in the vicinity O(U0)×O(λθ)0, and introduce the perturbed characteristic value λθ = (λθ)0 + ξ and the perturbed solution U = U0(x)+ζ(x). Following the method in Akhmedov (1957), we substituted these expressions in Eq. (10), written in the form
and taking into account the Taylor expansion Ψ(x, U) = ∑j = 0, 1, …ωj(x)ζj(x) (here ζ(x) = ∑k = 1ξkζk(x)),
we obtained a system of recurrent linear and multi-linear equations for the variables ζi(x)
Since, by assumption, 𝒟(λ0) ≠ 0, then for a linear non-uniform Fredholm II type equation (13) there exists a resolvent R(x, y; λ0), and we can write
(here the operator function ℋk is the sum of all integrals including ζ1, ζ2, … up to (k − 1)–th power: 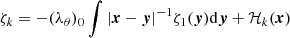 ).
).
Thus, we consistently and uniquely defined all functions ζk. Consequently, we constructed a power series for ζ(x) = ζ(ξi, ζi(x)) ≡ ξiζi (summation over repeating indices), and it only remains to prove that the constructed series converges (for all values from some convergence circle) for the deviation parameter ξ (this completely establishes the equivalence of the expansion ζ(ξi, ζi(x)) and the function ζ(x)).
Based on the properties of the Lyapunov–Schmidt integral operator with a weakly polar kernel (lemma 8.1 in Krasnosel’sky 1964), and explicit forms of ωk ∝ exp(−αx2 − U)/k!, we can state |∫Ω|x − y|−1ωk(y)dy|< Z1(=const) (k = 0, 1, …, ∀x ∈ Ω). Next, by definition, |R(x, y; λ0)| < Z2(=const) (∀x, y ∈ Ω). Then, we can write the major series for series ζ(ξi, ζi(x)). We introduced an algebraic equation ζ† = Z3(ξ + ξζ† + (ξ + (λθ)0)⋅((ζ†)2 + (ζ†)3 + …)), Z3 ≡ Z1(1 + Z2|(λθ)0|). We substituted ζ(x) = ξj𝜘j|j = 1, 2, … into the last equation and then compared the coefficients at different powers of the deviation variable ξ,
Consequently, |ζk(x)| < 𝜘k (x ∈ Ω), and the convergence region of the series ζ = Z3(ξ + ξζ + …) is equivalent to the convergence region of the series ζ(x) = ξjζj(x)|j = 1, 2, …. To define the convergence region of ζ = ξi𝜘i, we ought to investigate the implicit function ζ = Z3(ξ + ξζ + …) as a function of 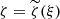
By the implicit function theorem (Deimling 2010), since 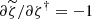 for ξ = ζ† = 0, then there exists a convergence circle with a positive radius for the series ζ† = Z3(ξ + ξζ† + (ξ + |(λθ)0|)((ζ†)2 + (ζ†)3 + …). Consequently, there exists a function ζ(x), and the function
for ξ = ζ† = 0, then there exists a convergence circle with a positive radius for the series ζ† = Z3(ξ + ξζ† + (ξ + |(λθ)0|)((ζ†)2 + (ζ†)3 + …). Consequently, there exists a function ζ(x), and the function
which is a holomorphic solution of the Hammerstein equation (10) in the vicinity O((λθ)0) (herewith lim(λθ)→(λθ)0U = U0).
We recall some of the properties of the linear compact operator 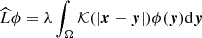 . The kernel of this operator is symmetric, of weak polar type; consequently, the operator
. The kernel of this operator is symmetric, of weak polar type; consequently, the operator 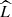 belongs to the Hilbert–Schmidt type of operators. The existence of at least one characteristic function has been known since Kellogg (Kellogg 1922). Moreover, there exists a sequence of characteristic values and corresponding eigenfunctions of the investigated kernel of the linear integral operator (theorem 146 in Titchmarsh 1957). In accordance with Kalmenov & Suragan (2011), we considered
belongs to the Hilbert–Schmidt type of operators. The existence of at least one characteristic function has been known since Kellogg (Kellogg 1922). Moreover, there exists a sequence of characteristic values and corresponding eigenfunctions of the investigated kernel of the linear integral operator (theorem 146 in Titchmarsh 1957). In accordance with Kalmenov & Suragan (2011), we considered
where φj(ℓ+1/2) are the roots of the transcendental equation
where 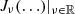 refers to the Bessel function of fractional order. The eigenfunctions corresponding to each eigenvalue λℓ, j can be represented in spherical coordinates in the form
refers to the Bessel function of fractional order. The eigenfunctions corresponding to each eigenvalue λℓ, j can be represented in spherical coordinates in the form 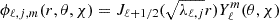 (|m|≤ℓ), Yℓm(θ, χ) = Pℓm(cos(θ))cos(mχ). It should be noted that we considered the Hammerstein equation (10) for an arbitrarily shaped region Ω, but for a spherical region, we assumed ℓ = m = 0 (
(|m|≤ℓ), Yℓm(θ, χ) = Pℓm(cos(θ))cos(mχ). It should be noted that we considered the Hammerstein equation (10) for an arbitrarily shaped region Ω, but for a spherical region, we assumed ℓ = m = 0 (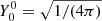 ). The kernel
). The kernel 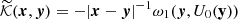 of the Fredholm equation for the potential belongs to the Schmidt class, and it can be transformed into symmetrical form,
of the Fredholm equation for the potential belongs to the Schmidt class, and it can be transformed into symmetrical form,
In this case, the resolvent for kernel 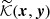 is equal to
is equal to 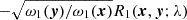 , where R1 is a resolvent for the symmetric kernel
, where R1 is a resolvent for the symmetric kernel 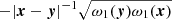 . In fact, ω1(y) is a weight for the Newtonian kernel. We denote
. In fact, ω1(y) is a weight for the Newtonian kernel. We denote 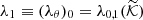 as the characteristic number to which the eigenfunction corresponds
as the characteristic number to which the eigenfunction corresponds 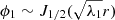 . To simplify the further calculations, we assumed ω1 ≡ 1 (this can always be accomplished by multiplying of the left- and right-hand sides of Eq. (11) by
. To simplify the further calculations, we assumed ω1 ≡ 1 (this can always be accomplished by multiplying of the left- and right-hand sides of Eq. (11) by 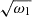 and redefining
and redefining 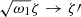 ,
, 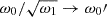 etc.). We searched for solutions of Eq. (11) in the form of a series ζ = ξiζi|i = 1, 2, …. After substituting the last series, we obtained a system of recurrent integral equations,
etc.). We searched for solutions of Eq. (11) in the form of a series ζ = ξiζi|i = 1, 2, …. After substituting the last series, we obtained a system of recurrent integral equations,
According to the Fredholm alternative, the condition of the existence of the solution for the first equation of the system is the orthogonality of the characteristic function ϕ1 and of the second term in the right-hand side of Eq. (19): 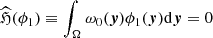 . This case is physically unrealizable (for ϕ1, ϕ2, …), which can be checked directly. This means the absence (in the neighborhood of the characteristic value λk, k ≥ 1) of the analytic solution of the non-linear equation for the gravitational potential. Therefore, we turn to case
. This case is physically unrealizable (for ϕ1, ϕ2, …), which can be checked directly. This means the absence (in the neighborhood of the characteristic value λk, k ≥ 1) of the analytic solution of the non-linear equation for the gravitational potential. Therefore, we turn to case 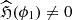 . Then, Eq. (14) is unsolvable (the condition of the Fredholm theorem is absent), and consequently, the analytic series ζ = ξiζi (for integer indices and powers) does not exist. However, we can consider the representation ζ(x) as a Puiseux series: ζ = ξk/2ζk|k = 1, 2, …. We denote ξ1/2 ≡ ν, and then, equation (11) takes the form
. Then, Eq. (14) is unsolvable (the condition of the Fredholm theorem is absent), and consequently, the analytic series ζ = ξiζi (for integer indices and powers) does not exist. However, we can consider the representation ζ(x) as a Puiseux series: ζ = ξk/2ζk|k = 1, 2, …. We denote ξ1/2 ≡ ν, and then, equation (11) takes the form
and as mentioned above, the Puiseux series takes the form ζ = νkζk|k = 1, 2, …. Substituting this series into equation (23), we obtain an infinite system of equations,
Then, we obtain 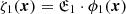 ,
, 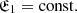 The condition (by the Fredholm alternative) for the existence of a solution of equation (25) can be written as
The condition (by the Fredholm alternative) for the existence of a solution of equation (25) can be written as
or, after integration by the variable x: ∫(λ1ω2ζ12(y)+ω0)ϕ1(y)dy = 0. When we substitute the obtained above expression 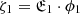 in this formula, then we have for the constant
in this formula, then we have for the constant 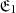 an explicit expression,
an explicit expression,
Equation (25) may be written as
In the general case n ≥ 3, we obtain
Here, 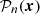 can be associated with the Ruston pseudo-resolvent (Ruston 1948). Consequently, we can write the series ζ = ξk/2ζk|k = 1, 2, ..., and this series formally satisfies Eq. (11). We ought to demonstrate the convergence of this series in the neighbourhood O(ξ). We introduce (1)the constant
can be associated with the Ruston pseudo-resolvent (Ruston 1948). Consequently, we can write the series ζ = ξk/2ζk|k = 1, 2, ..., and this series formally satisfies Eq. (11). We ought to demonstrate the convergence of this series in the neighbourhood O(ξ). We introduce (1)the constant 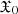 , defined by the condition
, defined by the condition 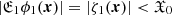 (∀x ∈ Ω), and (2)the function
(∀x ∈ Ω), and (2)the function 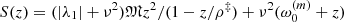 , where |ω0|< ω0(m), ρ‡ ∈ (0, ρmax‡), ρmax‡ is the convergence radius of the series ω2(x)+ω3(x)z + ω4(x)z2 + …,
, where |ω0|< ω0(m), ρ‡ ∈ (0, ρmax‡), ρmax‡ is the convergence radius of the series ω2(x)+ω3(x)z + ω4(x)z2 + …, 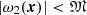 . We substitute in the definition S(z) the decomposition
. We substitute in the definition S(z) the decomposition 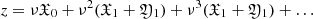 and formally obtain the series S(z) = ν2S2 + ν3S3 + …. The value Sn(z) is a major function for expression
and formally obtain the series S(z) = ν2S2 + ν3S3 + …. The value Sn(z) is a major function for expression 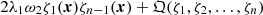 , and the condition
, and the condition 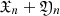 is a majorant function for ζn + 1(x), n = 1, 2, …
is a majorant function for ζn + 1(x), n = 1, 2, …
We denote (1)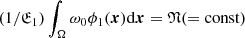 , (2)
, (2)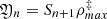 , and (3)
, and (3)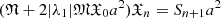 (a > |ϕ1(x)|). Consequently,
(a > |ϕ1(x)|). Consequently, 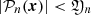 ,
, 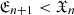 . We introduce the functions
. We introduce the functions 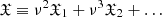 ,
, 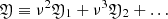 , and then, the above given definition of variables
, and then, the above given definition of variables 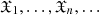 and
and 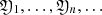 is equivalent to solving the system of equations
is equivalent to solving the system of equations
We replace the variables 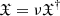 ,
, 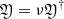 . Then, the system (32)–(33) takes the form
. Then, the system (32)–(33) takes the form
The Jacobi determinant of the latter system of equations is 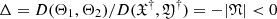 for
for 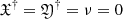 . Consequently, the series of defined variables
. Consequently, the series of defined variables 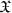 and
and 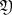 converges in the vicinity of the point ν = 0. The series
converges in the vicinity of the point ν = 0. The series 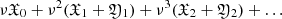 has a convergence circle (with a centre in the point ν = 0). This indicates that the Puiseux series ζ = ξk/2ζk|k = 1, 2, … converges in the vicinity of the point ξ = 0.
has a convergence circle (with a centre in the point ν = 0). This indicates that the Puiseux series ζ = ξk/2ζk|k = 1, 2, … converges in the vicinity of the point ξ = 0.
We can conclude that the Hammerstein equation for the gravitational potential in the vicinity O(λ1)∋λ (where λ1 is one of the characteristic values of the linear Fredholm equation for the Newton potential) has two non-holomorphic solutions of the form
We return to Eq. (10) and to the assumption that ((λθ)0, U0) is a characteristic value and the eigenvalue of the Hammerstein operator 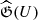 . The above analysis of the structure of the solutions of the Hammerstein equation used the fact that the kinetic temperature in the system was assumed to be positive (θ > 0). For negative temperatures (θ < 0), the properties of the solutions of the equation for the potential change slightly, although the method of their constructive continuation on the parameter plane remains the same. Since the presence of negative temperatures in the system is due to the effect of anti-gravity (due to the cosmological term in the integral equation), we assumed the Newtonian kernel to be continuous and a bounded function (although we can also use the Hilbert-Schmidt theory), and, on the basis of theorem 2 in Jingxian & Bendong (1997), we conclude that Eq. (10) has at least two analytic solutions outside the points of the spectrum of the Fréchet derivative of the Hammerstein operator
. The above analysis of the structure of the solutions of the Hammerstein equation used the fact that the kinetic temperature in the system was assumed to be positive (θ > 0). For negative temperatures (θ < 0), the properties of the solutions of the equation for the potential change slightly, although the method of their constructive continuation on the parameter plane remains the same. Since the presence of negative temperatures in the system is due to the effect of anti-gravity (due to the cosmological term in the integral equation), we assumed the Newtonian kernel to be continuous and a bounded function (although we can also use the Hilbert-Schmidt theory), and, on the basis of theorem 2 in Jingxian & Bendong (1997), we conclude that Eq. (10) has at least two analytic solutions outside the points of the spectrum of the Fréchet derivative of the Hammerstein operator 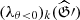 . In the vicinity of the characteristic points corresponding to the solutions of the non-linear equation and simultaneous coincidence with the special points of the resolvent of the linearized equation, the solutions are continued algebraically and can be written out in the form of Puiseux series on half-integer degrees of the deviation from the solution points.
. In the vicinity of the characteristic points corresponding to the solutions of the non-linear equation and simultaneous coincidence with the special points of the resolvent of the linearized equation, the solutions are continued algebraically and can be written out in the form of Puiseux series on half-integer degrees of the deviation from the solution points.
In physical terms, the expression (36) can be written as
where U0(x) is a solution of the Hammerstein equation for the potential (existing due to the properties of the corresponding integral operator), λ1(=λθ)0) is the characteristic value of kernel ω1/|x − y| (for the Fredholm equation) in the vicinity of the point λθ ∈ ((λθ)0 − ϵ, (λθ)0 + ϵ). If sgn(∫Ωω0ϕ1(y)dy) ≠ sgn(∫Ωλ1ω2ϕ13(y)dy), then for λ > λ1 there exist two solutions, and for λ < λ1 there are no solutions. For sgn(∫Ωω0ϕ1(y)dy) = sgn(∫Ωλ1ω2ϕ13(y)dy), then for λ < λ1 there exist two solutions, and for λ > λ1 there are no solutions.
Thus, we showed that the solution of the system of Vlasov-Poisson equations in the case of using the energy substitution in the stationary Vlasov equation and choosing the quasi-Maxwell distribution (depending on the kinetic temperature) as a basis solution of the kinetic equation, leads to the non-linear Hammerstein integral equation for the potential, including repulsion due to the cosmological term in Eq. (1). The Hammerstein equation in essence is an equation for the self-consistent field in the system of massive many-particles on cosmological scales. This leads to the simultaneous realisation in the cosmological system with a self-consistent field of two types of ordering: A significant increase in the matter density and its decrease (at the one-dimensional motion of matter in the channel, walls appear with a high value of the gravitational potential, and voids, which are practically empty spaces between walls). Oscillations of the eigenfunctions even in the simplest case of spherical symmetry of the Green function can form analogues of interference patterns, which leads to the production of structure formation in a homogeneous medium far from the line that connects the massive objects. Since the eigenfunctions of the linearised version of the equation for the potential are proportional to the Bessel function (with a rapidly decreasing weight function), the loss of periodicity of the solutions in physical space becomes obvious. Since for non-linear integral operators it is possible to establish the the continuum character of the spectrum, we can observe the effect of secondary solutions (on the hyperplane of parameters near the basic solution of the equation) that coexist with the initial solutions, which leads to the construction of the second type of periodicity: The translation of the solution isotropically along all directions. Thus, the composition of solutions with a potential of two types in the presence of additional translational transgression due to the structure of the spectrum results in a distribution of the field and matter in space that is peculiar to the cosmic web. The scaling of the semi-periodic structures corresponds to the scale of the involved constant, that is, the cosmological constant in agreement with observational data (Gurzadyan et al. 2023a,b). Incidentally, the change in the kinetic temperature at the zero-point transition can lead to a dipole-type structures involving a repeller.
The study performed above of the properties of solutions of the non-linear inhomogeneous integral Hammerstein equation obtained from the Dirichlet boundary value problem allowed us without the need to invoke the assumption of a correlation of fluctuations to describe in a completely deterministic manner the existence in the vicinity of equilibrium points of many-particle systems (at different scales) defined by secondary solutions with significantly different properties. We also proved in this analysis that these solutions exist non-locally. The presence of analytical and non-holomorphic branches of solutions of the equation for the potential given by Eq. (10) from a physical point of view in distinguished directions with sharp gradients of the density parameter of the medium has to be associated with the walls as the internal spaces between the voids. It should be noted that the cosmological term in the Hammerstein equation leads to the necessity of introducing of the concept of a modified kinetic temperature as defined by Vlasov (Vlasov 1961, 1978). In contrast to the linear analysis based on the properties of the Fredholm equations of the second kind, which, as was previously established by the authors (Gurzadyan et al. 2022, 2023a,b), should lead to periodic and mixed-periodic cosmological structures, the method proposed in this study is more refined and suitable for numerical modelling. It can be used in certain cases as an alternative to statistical computations.
4. Conclusions
We performed an analysis of the filament formation in the late Universe based on the Vlasov kinetic technique and using the modified law of gravitational interaction with a cosmological constant, Eq. (1). While the primordial density fluctuations were considered to lead to an early structure formation via the Zeldovich pancake theory, that is, via stochastic dynamics, the Vlasov self-consistent field mechanism can provide structure features at late stages of the evolution.
We continued the rigorous analysis of the Vlasov-Poisson equations of Gurzadyan et al. (2022, 2023a,b). The equations reduced to the Hammerstein integral equation were shown to predict semi-periodic structures, that is, those peculiar to the cosmic web. The role of the repulsive term, that is, of the cosmological constant, is a key role because it is also defines the scaling of the formed semi-periodic structures, that is, of the voids. In this context, the considered mechanism of the formation of the structures in the local Universe complements the role of the cosmological constant term in Eq. (1) in the appearance of two galactic flows. The local flow is determined by the in McCrea-Milne non-relativistic model, and the global flow is determined by the Friedmann equations, while the discrepancy of the Hubble constants of the flows thus naturally explains the Hubble tension.
Thus, the Hubble tension (Riess et al. 2024a,b; Scolnic et al. 2024a,b) and other observational indications of the possible genuine difference in the properties of the early and late Universe can serve as tests for the mechanism of the structure formation on the local scale, as discussed above. In particular, the measurement by the Dark Energy Spectroscopic Instrument (DESI) collaboration (Said et al. 2024) of the local value of the Hubble constant and the distance to the Coma cluster using the fundamental plane of galaxies confirmed this tension. An additional informative window for tracing the cosmological evolution arises from the released DESI first-year data (Adame et al. 2024a,b,c) on the baryon acoustic oscillation using several tracers. The data revealed additional tensions with the ΛCDM model. These observational data support the approach of our study, that is, the need of developing different, more refined descriptions of the properties of the late Universe. In particular, this approach, in which the scaling radius rc = (Gm/(3Λc2))1/3 defined the role of the cosmological constant term in Eq. (1), enabled us to fit the dynamics of the galactic flow in the vicinity of the Virgo supercluster or the Laniakea supercluster, for instance (Gurzadyan & Stepanian 2021a,b).
The revelation of the dominating role of the self-consistent gravitational field in the formation of the cosmic structures on local cosmological scales can be considered the main result of our rigorous analysis. The refined comparison of the predictions of the considered mechanism with the observational surveys on the voids and of the filaments, for example, to study the distributions of their scales versus redshift, can therefore be of particular interest.
Acknowledgments
We are thankful to the referee for valuable comments. VMC is acknowledging the Russian Science Foundation grant 20-11-20165.
References
- Adame, A. G., Aguilar, J., Ahlen, S., et al. 2024a, ArXiv e-prints [arXiv:2404.03000] [Google Scholar]
- Adame, A. G., Aguilar, J., Ahlen, S., et al. 2024b, ArXiv e-prints [arXiv:2404.03001] [Google Scholar]
- Adame, A. G., Aguilar, J., Ahlen, S., et al. 2024c, ArXiv e-prints [arXiv:2404.03002] [Google Scholar]
- Akhmedov, K. T. 1957, Uspekhi Mat. Nauk, 12, 135 [Google Scholar]
- Arnold, V. I. 1982, Comm. Petrovskij seminar, 8, 21 [NASA ADS] [Google Scholar]
- Arnold, V. I., Shandarin, S. F., & Zeldovich, Ya. B. 1982, Geophys. Astrophys. Fluid Dynamics, 20, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bajardi, F., D’Agostino, R., Benetti, M., De Falco, V., & Capozziello, S. 2022, Eur. Phys. J. Plus, 137, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Bateman, H., & Erdelyi, A. 1955, Higher Transcendental Functions, 3 (New York - Toronto - London: McGraw-Hill Book Company) [Google Scholar]
- Bouchè, F., Capozziello, S., Salzano, V., & Umetsu, K. 2022, Eur. Phys. J. C, 82, 652 [CrossRef] [Google Scholar]
- Capozziello, S., & D’Agostino, R. 2023, Phys. Dark Universe, 42, 101346 [NASA ADS] [CrossRef] [Google Scholar]
- Capozziello, S., & Lambiase, G. 2022, Eur. Phys. J. Plus, 137, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Capozziello, S., Sarracino, G., & De Somma, G. 2024, Universe, 10, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Corduneanu, C. 1991, in Integral Equations and Applications (Cambridge-N.Y.-Port Chester-Melbourne-Sydney: Cambridge University Press) [CrossRef] [Google Scholar]
- Dainotti, M., De Simone, B., Montani, G., et al. 2023, ArXiv e-prints [arXiv:2301.10572] [Google Scholar]
- Deimling, K. 2010, Nonlinear Functional Analysis (New York: Dover Publications Inc) [Google Scholar]
- de Pedreira, I., et al. 2024, Phys. Rev. D, 109, 103525 [CrossRef] [Google Scholar]
- Di Valentino, E., Olga, M., Pan, S., et al. 2021, Class. Quant. Grav., 38, 153001 [NASA ADS] [CrossRef] [Google Scholar]
- Dupaigne, L. 2011, Stable solutions of elliptic partial differential equations (Boca Raton (FL): Chapman& Hall/CRC) [CrossRef] [Google Scholar]
- Fimin, N. N., & Chechetkin, V. M. 2020, The Physical Foundations of Hydrodynamic Processes: Macroscopic and Kinetic Approaches (World Scientific) [CrossRef] [Google Scholar]
- Gurzadyan, V. G. 1985, Observatory, 105, 42 [NASA ADS] [Google Scholar]
- Gurzadyan, V. G. 2019, Eur. Phys. J. Plus, 134, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2018, Eur. Phys. J. C, 78, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2019, Eur. Phys. J. C, 79, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2020, Eur. Phys. J. C, 80, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2021a, Eur. Phys. J. Plus, 136, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V. G., & Stepanian, A. 2021b, A&A, 653, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., Fimin, N. N., & Chechetkin, V. M. 2022, A&A, 666, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., Fimin, N. N., & Chechetkin, V. M. 2023a, A&A, 672, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., Fimin, N. N., & Chechetkin, V. M. 2023b, A&A, 677, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hewitt, E., & Savage, L. J. 1955, Trans. Am. Math. Soc., 80, 470 [Google Scholar]
- Jingxian, S., & Bendong, L. 1997, Nonlin. Anal. Theor. Meth. Appl., 29, 1277 [CrossRef] [Google Scholar]
- Kalmenov, T. S. h., & Suragan, D. 2011, in A Boundary Condition and Spectral Problems for the Newton Potential, in: Modern Aspects of the Theory of Partial Differential Equations, eds. M. Ruzhansky, & J. Wirth (Birkhauser), Operator Theory: Advances and Applications, 216, 187 [CrossRef] [Google Scholar]
- Keller, H. B., & Langford, W. F. 1972, Arch. Rat. Mech. Anal., 48, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kellogg, O. D. 1922, Math. Annalen, 86, 14 [CrossRef] [Google Scholar]
- Krasnosel’sky, M. A. 1964, Topological Methods in the Theory of Nonlinear Integral Equations (Macmillan Co.) [Google Scholar]
- Kravtsov, A. V. 2013, ApJ, 764, L31 [NASA ADS] [CrossRef] [Google Scholar]
- McCrea, W. H., & Milne, E. A. 1934, Q. J. Math., 5, 73 [CrossRef] [Google Scholar]
- Nowakowski, M. 2001, Int. J. Mod. Phys. D, 10, 649 [NASA ADS] [CrossRef] [Google Scholar]
- O’Regan, D., & Meehan, M. 1998, Existence Theory for Nonlinear Integral and Integrodifferential Equations (Kluwer Academic Publishers) [Google Scholar]
- Peebles, P. J. E. 1993, Principles of Physical Cosmology (Princeton: Princeton University Press) [Google Scholar]
- Pokhozhaev, S. I. 2010, Diff. Equations, 46, 530 [CrossRef] [Google Scholar]
- Riess, A. G. 2020, Nat. Rev. Phys., 2, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Anand, G. S., Yuan, W., et al. 2024a, ApJ, 962, 17 [Google Scholar]
- Riess, A. G., Scolnic, D., Anand, G. S., et al. 2024b, ApJ, 977, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Ruston, A. F. 1948, Proc. London Math. Soc., 2, 53 [Google Scholar]
- Said, K., Howlett, C., Davis, T., et al. 2024, ArXiv e-prints [arXiv:2408.13842] [Google Scholar]
- Scolnic, D., Riess, A. G., Murakami, Y. S., et al. 2024a, ArXiv e-prints [arXiv:2409.14546] [Google Scholar]
- Scolnic, D., Boubel, P., Byrne, J., et al. 2024b, ArXiv e-prints [arXiv:2412.08449] [Google Scholar]
- Shandarin, S. F., & Zeldovich Ya. B., 1989, Rev. Mod. Phys., 61, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Titchmarsh, E. C. 1957, Introduction to the Theory of Fourier Integrals (Oxford: Oxford University Press) [Google Scholar]
- Vedenyapin, V., Sinitsyn, A., & Dulov, E. 2011, Kinetic Boltzmann (Elsevier Insights: Vlasov and Related Equations) [Google Scholar]
- Vedenyapin, V. V., Fimin, N. N., & Chechetkin, V. M. 2021, Eur. Phys. J. Plus, 136, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Vlasov, A. A. 1961, Many Particle Theory and its Application to Plasma (Gordon and Breach) [Google Scholar]
- Vlasov, A. A. 1978, Nonlocal Statistical Mechanics (Moscow: Nauka). (in Russian) [Google Scholar]
- Zabreiko, P. P., Koshelev, A. I., Krasnoselsky, M. A., et al. 1975, Integral Equations (Leyden: Noordhoff International Pub.), 443 [Google Scholar]
- Zeldovich, Ya. B. 1970, A&A, 5, 84 [Google Scholar]
- Zeldovich, Ya. B. 1981, Non-relativistic cosmology, Editor’s appendix 1 to Russian edition of S. Weinberg, The First Three Minutes (Moscow: Energoizdat), 181 [Google Scholar]
- Zemyan, S. M. 2012, The Classical Theory of Integral Equations: A Concise Treatment (Springer Science+Business Media) [CrossRef] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



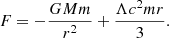
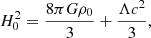
![$$ \begin{aligned} \frac{\partial F(\boldsymbol{x},\boldsymbol{v},t)}{\partial t} + {\mathrm{div}}_{\boldsymbol{x}}(\boldsymbol{v}F)+\widehat{G}(F;F) = 0,\nonumber \\~~~ \widehat{G}(F; F) \equiv -\big ({{\nabla }}_{\boldsymbol{v}}F\big ) \big ({\nabla }_{\boldsymbol{x}} (\Phi [F(\boldsymbol{x})]\big )), \end{aligned} $$](/articles/aa/full_html/2025/02/aa53679-25/aa53679-25-eq3.gif)
![$$ \begin{aligned} {\Delta }_{\boldsymbol{x}}^{(3)}\Phi [F(\boldsymbol{x})]\big |_{t=t_0}= A S_3 G \int F(\boldsymbol{x},\boldsymbol{v},t_0)\,\mathrm{d}\boldsymbol{v} - \frac{c^2\Lambda }{2}, \end{aligned} $$](/articles/aa/full_html/2025/02/aa53679-25/aa53679-25-eq4.gif)
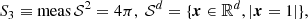
![$$ \begin{aligned} \widehat{G}(F; F)&= \boldsymbol{G}(F)\frac{\partial F}{\partial \boldsymbol{v}},~~~ \\ \boldsymbol{G}(F)&=-\nabla _{\boldsymbol{x}}\Phi [F(\boldsymbol{x})],\nonumber \end{aligned} $$](/articles/aa/full_html/2025/02/aa53679-25/aa53679-25-eq7.gif)
![$$ \begin{aligned} \Phi [F(\boldsymbol{x})]= AS_3 G \int \int {\mathfrak{K} }_3 (\boldsymbol{x}-\boldsymbol{x}\prime ) F(\boldsymbol{x}\prime ,\boldsymbol{v}\prime ,t_*)\,\mathrm{d}\boldsymbol{x}\prime \mathrm{d}\boldsymbol{v}\prime \\ + \frac{\Lambda c^2}{12}|\boldsymbol{x}|^2 + \widehat{\mathfrak{B} }_3 (\boldsymbol{x},\boldsymbol{x}\prime ), \end{aligned} $$](/articles/aa/full_html/2025/02/aa53679-25/aa53679-25-eq8.gif)
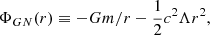
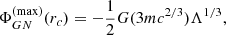
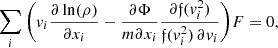
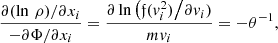
![$$ \begin{aligned} \Delta \Phi (\boldsymbol{x}) = ANG S_3^2 \bigg (\int _{y\in [0,\infty ]} \exp \big (-y^2/(2\theta ) \big )y^2\,\mathrm{d}y \bigg )\cdot \end{aligned} $$](/articles/aa/full_html/2025/02/aa53679-25/aa53679-25-eq17.gif)