| Issue |
A&A
Volume 696, April 2025
|
|
|---|---|---|
| Article Number | A170 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202453204 | |
| Published online | 21 April 2025 | |
New routes for PN destruction and formation in the interstellar medium via neutral-neutral gas-phase reactions and an extended database for reactions involving phosphorus
1
Departamento de Física, Universidade Federal do Espírito Santo,
Av. Fernando Ferrari 514,
Vitória,
ES
29075-910,
Brazil
2
Dept. Ciencias Integradas, Facultad de Ciencias Experimentales, Centro de Estudios Avanzados en Física, Matemática y Computación, Unidad Asociada GIFMAN, CSIC-UHU,
Universidad de Huelva,
Spain
3
Departamento de Química, Centro Federal de Educação Tecnológica de Minas Gerais,
Av. Amazonas 5253,
Belo Horizonte,
MG
30421-169,
Brazil
4
Instituto Universitario “Carlos I” de Física Teórica y Computacional,
Universidad de Granada,
Spain
5
School of Physics and Physical Engineering Qufu Normal University,
Qufu, Shandong
273165,
China
6
Coimbra Chemistry Centre and Chemistry Department, University of Coimbra,
3004-535
Coimbra,
Portugal
★ Corresponding author; edgar.mendoza@dci.uhu.es
Received:
28
November
2024
Accepted:
4
March
2025
Context. Phosphorus plays an essential role in the chemistry of living organisms, being present in several fundamental biomolecules. The investigation of chemical reactions taking place in different astronomical environments involving phosphorus-containing molecules is essential for understanding how these species are produced and destroyed. Ultimately, it can help unravel the pathways that lead to important prebiotic molecules.
Aims. Phosphorus monoxide (PO) and phosphorus nitride (PN) are key reservoirs of phosphorus in the Interstellar Medium (ISM). Understanding their reaction mechanisms and accurately predicting rate coefficients are crucial for modelling phosphorus chemistry in space. This work presents a computational study of the CPN system to identify viable reaction pathways involving atom-diatom collisions and to explore a potential destruction route for PN in the ISM. We also evaluate the role of several neutral-neutral reactions involving PO and PN in chemical models simulating interstellar environments.
Methods. In this work we explore the potential energy landscape of the C(3P) + PN(1Σ+), N(4S) + CP(2Σ+) and P(4S) + CN(2Σ+) reactions by performing high-accuracy ab initio calculations and provide their rate coefficients over a wide range of temperatures. The temperature-dependent rate coefficients were fitted to the modified Arrhenius equation: k(T) = α(T/300)βexp(−γ/T). An updated chemical network for P-bearing species was used to model the time-dependent abundances and reaction contributions of P, PO, PN, and PH (phosphinidene) during the chemical evolution of diffuse and translucent clouds and dense clouds.
Results. The only neutral-neutral reaction capable of destroying PN without an activation energy seems to be the PN + C one. We have also shown that reactions between CP and N can yield CN and PN barrierlessly. Chemical models indicate that PO is a crucial species driving the gas-phase formation of PN. Typically, PO/PN ratios exceed 1, though their chemistry is influenced by photon- and cosmic-ray-induced processes. Over time in simulated dense clouds, neutral-neutral reactions such as PO + N, PH + N, P + OH, and PH+O play a significant role in determining the relative abundances of PO and PN.
Key words: astrochemistry / molecular processes / ISM: abundances / ISM: clouds / ISM: molecules
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Phosphorus is present in several molecules that are essential for life as we know it, although it is still a mystery how it became biologically available on Earth, possibly from an inorganic mineral or even extraterrestrial sources (Pasek & Lauretta 2005; Schwartz 2006). When combined with four oxygen atoms, it yields the phosphate ion (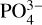 ), which is highly soluble in water and whose salts are plentiful on Earth and were readily available throughout the development of life (Hunter 2012).
), which is highly soluble in water and whose salts are plentiful on Earth and were readily available throughout the development of life (Hunter 2012).
There is now biochemical evidence that indicates that phosphate may indeed have played an important role in the chemical origins of life. Several feasible environments capable of producing phosphates are currently conceivable, providing numerous potential solutions to the issue of phosphate availability (Fernández-García et al. 2017). Phosphorus, as well, can form P−N (phosphoramidate), P−S (phosphorothioate) and P−C (phosphonate) linkages, all of which are present in nature. For instance, phosphorylation of amino acids such as histidine, lysine and arginine to generate high energy phosphoramidate bonds may have been crucial under prebiotic circumstances (Hunter 2012).
The prebiotic chemistry (including P-bearing molecules) on our planet may have been enriched by the bombardment of extraterrestrial bodies such as comets and asteroids (Pasek & Lauretta 2005; Altwegg et al. 2016; Fernández-Ruz et al. 2023). For this reason, the investigation of chemical processes taking place on different astronomical environments such as molecular clouds and star forming-regions is of great importance to our understanding of the primordial chemistry of phosphorus on Earth.
The detection of most P-bearing species in space has been restricted so far to the circumstellar envelopes of evolved stars (Guélin et al. 1990; Agúndez et al. 2007; Halfen et al. 2008; Milam et al. 2008; Agúndez et al. 2014a; Agúndez et al. 2014b) in our Galaxy and planetary atmospheres (Bregman et al. 1975; Larson et al. 1977). However, special attention has been given to phosphorus monoxide (PO) and phosphorus nitride (PN), which were the only ones also detected towards star-forming regions (Fontani et al. 2016; Rivilla et al. 2016; Mininni et al. 2018; Bergner et al. 2019; Fontani et al. 2019; Rivilla et al. 2020; Bernal et al. 2021), in addition to the interstellar medium (ISM) (Turner & Bally 1987; Ziurys 1987), circumstellar envelopes of evolved stars (Tenenbaum et al. 2007; Milam et al. 2008; Ziurys et al. 2018), protostellar shocks (Yamaguchi et al. 2011; Lefloch et al. 2016) and Galactic Centre molecular clouds (Rivilla et al. 2018).
It has already been discussed that PO and PN may constitute the main reservoir of phosphorus in the gas phase in the ISM (Thorne et al. 1984; Tenenbaum et al. 2007; De Beck et al. 2013; Lefloch et al. 2016). In low-mass star-forming regions, PN was the first P-bearing molecule to be detected (Yamaguchi et al. 2011), while PO was first detected five years later towards the same solar-type star-forming region (L1157-B1) (Lefloch et al. 2016). The abundances of these species in such environments seem to be comparable, with PO being systematically more abundant than PN (Rivilla et al. 2016; Lefloch et al. 2016; Rivilla et al. 2018; Bergner et al. 2019). However, the small number of detection makes it difficult to precisely elucidate the mechanisms of formation of these molecules.
More recently, the presence of PO and PN in the gas phase has also been reported for the first time at the edge of our galaxy (Koelemay et al. 2023). The characteristic rotational lines of these P-bearing species were observed in the dense cloud WB89-621 (located 22.6 kpc from the Galactic Centre) and their abundances are comparable to values near the Solar System (Bernal et al. 2021; Koelemay et al. 2023). Specifically, the phosphorus nitride molecule has been detected for the first time in an extra-galactic environment towards two giant molecular clouds of NGC 253 (Haasler et al. 2022). The authors report a derived abundance ratio between PN and the shock-tracer SiO that follows the same trend already found towards Galactic sources (Rivilla et al. 2018; Haasler et al. 2022).
Noticeably, the [PO]/[PN] ratio has consistently been found to be >1, independently of the source, with values up to ∼6 (Haasler et al. 2022; Fernández-Ruz et al. 2023). However, the available astrochemical models most frequently fail to reproduce this trend, usually predicting [PO]/[PN] ratios <1 for various different physical conditions (Jiménez-Serra et al. 2018; Chantzos et al. 2020; Sil et al. 2021; Fernández-Ruz et al. 2023). Various factors could contribute to such disparities, including the inadequacy of the phosphorus chemical network and the considerable uncertainties associated with reaction rate coefficients (Fernández-Ruz et al. 2023). Currently, there is compelling evidence indicating that PO emerges in the gaseous phase prior to PN and then vanishes, whereas PN lingers on for a certain time (Gomes et al. 2023b). The precise mechanisms accountable for their formation and decomposition are yet to be better delineated and their study may solve the inconsistency between astrochemical models and observations.
A computational approach can help in understanding the chemistry of phosphorus in the gas phase since experimental studies involving these P-bearing compounds are scarce in the literature. García de la Concepción et al. (2021) obtained rate coefficients and branching ratios for the reactions P + OH → PO + H and P + H2O → PO + H2 using ab initio transition state theory (TST) and employing high-level quantum chemical calculations. The authors conclude that the formation of PO, in the gas phase, from OH and P in their ground state is highly favourable, but should not occur if P is in its first excited electronic state. As for the reaction between P and H2O, the predicted trend is the opposite. More recently, the P(4S) + O2(3Σ−) and P(4S) + O2(1Δ) reactions were also investigated by Gomes et al. (2022) and García de la Concepción et al. (2024) from a theoretical point of view, and the mechanisms towards PO formation could be elucidated. It has been concluded that multireference methods are needed to properly describe the system and that the P(4S) + O2(3Σ−) reaction dominates the formation of PO when OH is not sufficiently available (for instance, in regions where shock speeds are below 40 km s−1). Structural, molecular and spectroscopic properties of the HPO system were studied using the coupled cluster method by Francisco (2003) and Puzzarini (2006), and isomerisation and dissociation energies were obtained, showing that the two processes may compete with each other.
Plane et al. (2021) estimated a series of rate coefficients for several reactions of the HxPOy system from electronic structure calculations and subsequent application of statistical rate theory. In the following year, Douglas et al. (2022) gathered an extensive network of reactions involving phosphorus with estimates for their rate coefficients obtained from electronic structure calculations at the Complete Basis Set (CBS-QB3) level (Montgomery et al. 2000).
Our research group has also approached the NPO system using high-level electronic structure methods (Souza et al. 2021) and quantitatively confirmed that the depletion of PO by N atoms occurs fast, with a branching ratio favourable to the O + PN channel relative to P + NO. The HPN system was also addressed (Gomes et al. 2023a) using ab initio calculations and the variable reaction coordinate transition state theory (VRC-TST) and it was predicted that the reactions P(4S) + NH(3Σ−) and N(4S) + PH(3Σ−) occur without an activation barrier and are relevant for PN formation in the interstellar medium.
Astrochemical models, however, appear to lack important PN destruction pathways (Fernández-Ruz et al. 2023). This may be one reason for the failure to correctly predict the [PO]/[PN] ratio. Previous studies from our research group indicate that PN destruction by H atoms should not occur (Gomes et al. 2023a). However, PN destruction by N atoms may occur in high temperature environments, such as in shock regions (Gomes et al. 2023b). Jiménez-Serra et al. (2018) drew attention to the fact that the reactions N + CP → PN + C and P + CN → PN + C, proposed by Agúndez et al. (2007), have very uncertain rate coefficients and that the results of different models are little affected by the inclusion of these reactions. In the work of Fernández-Ruz et al. (2023), the parameters associated with the analogous reaction N + CN → N2 + C were used in the rate coefficients of the N + CP and P + CN reactions, assuming that the similarity between N and P should lead to similar chemical behaviour.
Therefore, in the present work, we focus on the computational study of the CPN system using the highest-level electronic structure methods available combined with TST. The main goals are to elucidate the viable reaction pathways involving simple atom-diatom collisions within this system (C3P) + PN(1 Σ+), N(4S) + CP(2 Σ+) and P(4S) + CN(2Σ+)), providing the respective rate coefficients and evaluating a possible route for the destruction of PN in the interstellar medium. We summarise other relevant reactions from the literature, and include them in the Kinetic Database for Astrochemistry (KIDA) (Wakelam et al. 2012) network to investigate the most important reactions that drive the abundances of PO and PN in the ISM.
2 Methodology
2.1 Electronic structure calculations
All electronic structure calculations reported here were performed using the MOLPRO (Werner et al. 2015) package. For the initial exploration of the potential energy surface (PES) of the PCN system, a density functional theory (DFT) (Kohn & Sham 1965) approach was employed using the aug-cc-pV(T+d)Z (Dunning 1989; Kendall et al. 1992) basis set (henceforth referred to as AV(T + d) Z) with the M06-2X (Zhao & Truhlar 2008) exchange and correlation functional. At this stage, stationary points were found and vibrational analysis was performed to confirm whether the obtained structures corresponded to energy minima or to first order saddle points on the PES. Intrinsic reaction coordinate (IRC) calculations were performed for all transition states (TSs) found in order to ensure their connection to the correct energy minima structures. All the obtained energies were zero-point energy (ZPE) corrected. In order to improve the accuracy of the energy values, further single-point energy calculations at the explicitly correlated coupled cluster (CCSD(T)-F12/cc-pVTZ-F12) (Adler et al. 2007; Knizia et al. 2009) level were performed over the geometries optimised at the DFT level and we name this methodology CCSD(T)-F12/VTZ-F12//M06-2X/AV(T+d)Z + ZPE(M06-2X/AV(T+d)Z). We have not employed scaling factors in the vibrational frequencies.
In a second stage, in order to account for a possible multiconfigurational character of the PCN system, all the previously obtained results were fully re-optimised within the ab initio full valence complete active space self-consistent field (CASSCF) (Szalay et al. 2012) level with AV(T + d) Z basis set. In this approach, the 1 s orbitals of C and N, and the 1s, 2s and 2p orbitals of P were considered as core orbitals, leading to an active space of 12 orbitals with 14 electrons. Vibrational analysis was also carried out and ZPEs were obtained for all stationary points on the CASSCF PES. This time, the accuracy of the energy values was enhanced by performing singlepoint energy calculations over all structures with the explicitly correlated multireference configuration interaction (MRCI-F12) (Szalay et al. 2012; Shiozaki et al. 2011) method, including the relaxed-reference Davidson correction to approximate quadruple excitations and also using the AV(T + d) Z basis set. The results reported for this methodology are referred here as MRCIF12/AV(T+d)Z//CAS/AV(T+d)Z + ZPE(CAS/AV(T+d)Z).
The methodologies employed here could also provide the magnitude of the dominant configuration in the CI wavefunctions (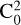 ) and the T1 diagnostic of all stationary points, which allows the assessment of the multireference character (MR) of the system (Lee & Taylor 1989; Leininger et al. 2000; Lee 2003). Lastly, the Wxmacmolplt and Avogadro software were used for graphical visualisation and representation of the molecular geometries (Bode & Gordon 1998; Hanwell et al. 2012).
) and the T1 diagnostic of all stationary points, which allows the assessment of the multireference character (MR) of the system (Lee & Taylor 1989; Leininger et al. 2000; Lee 2003). Lastly, the Wxmacmolplt and Avogadro software were used for graphical visualisation and representation of the molecular geometries (Bode & Gordon 1998; Hanwell et al. 2012).
2.2 Rate coefficients
In order to assess the effects of the reactions studied in this work on the relative abundances of the involved species, their rate coefficients must be calculated so that the chemical processes taking place in an interstellar environment can be simulated. We have obtained rigid rotor and harmonic oscillator rate coefficients using standard TST and including the Eckart tunnelling correction (Eckart 1930) employing the Master Equation System Solver (MESS) software package (Georgievskii et al. 2013). Phase space theory (PST) (Pechukas & Light 1965; Chesnavich 1986), as implemented in MESS, is used for the barrierless capture steps. For such cases, we have fitted the MRCI-F12/AV(T+d)Z energies obtained along the minimum energy path as a function of the internuclear separation (r) to the −C6/r6 function to obtain C6, which is then used in the PST calculation.
2.3 Astrochemical modelling
We utilised the Nautilus gas-grain code to simulate chemical abundances under interstellar conditions, focusing on the gas-phase and grain-surface processes described in the three-phase model by Ruaud et al. (2016). The gas-phase chemical network is based on the comprehensive kida.uva. 2014 database (Wakelam et al. 2015), which compiles extensive reaction pathways and kinetic data. Although the kida.uva. 2024 update has introduced new species and reaction channels, it does not modify phosphorus chemistry (Wakelam et al. 2024). In this work, we expanded the chemical network within Nautilus to include updated reaction pathways for phosphorus-containing molecules. This enabled the prediction of abundances for key astrochemical species such as PO and PN, whose formation mechanisms in extreme environments remain poorly understood. The study also assessed the significance of individual reaction pathways in phosphorus chemistry. Cosmic ray and X-ray ionisation rates, crucial drivers of interstellar chemical reactions, were systematically varied in the simulations. The default cosmic ray ionisation rate (ζCR) is typically set to 1.3 × 10−17 s−1 (Dalgarno 2006), but can reach 10−15 s−1 in regions like the central molecular zone of Sgr B2 (Goto et al. 2014). Similarly, X-ray ionisation rates (ζX) influence the chemistry of small neutrals and molecular ions, particularly in protostellar envelopes (Stäuber et al. 2005; Notsu et al. 2021). We tested ζCR values from 1.3 × 10−17 to 1.3 × 10−16 s−1 and ζx values from 1 × 10−18 to 1 × 10−17 s−1 to evaluate their effects on phosphorus chemistry.
Simulations were conducted to examine phosphorus chemistry under two distinct astrophysical conditions: diffuse and translucent clouds and dense clouds (Corby et al. 2018; Phan et al. 2018; Wolfire et al. 2022). In the diffuse and translucent model, the H2 gas density was set to 103 cm−3, with a temperature of 70 K and a visual extinction (AV) of less than 5 mag. The simulation covered a timescale of 1 Myr, during which cosmic ray and X-ray ionisation rates were varied to assess their impact on chemical processes. For the dense molecular cloud model, the gas density was increased to 104 cm−3, while the temperature was lowered to 30 K and AV was fixed at 10 mag. Simulations extended from 1 × 106 yr up to 1 × 108 yr to explore long-term chemical evolution. Ionisation rates were held constant at ζCR = 1.3 × 10−17 s−1 and ζx = 1 × 10−18 s−1. In both models, abundances were calculated as functions of time. The non-linear nature of the chemical network and the dynamic interplay of reactions prevented the system from reaching full equilibrium, influencing the steady-state abundances (Roueff & Le Bourlot 2020; Dufour et al. 2023). In the dense cloud model, extended simulations provided insights into the stability and evolutionary patterns of phosphorus-bearing species. Individual reaction contributions were evaluated to quantify their roles in shaping chemical pathways and the long-term persistence of these molecules in interstellar environments.
3 Results
3.1 Reaction products
As we expect the reactants (C(3P) + PN(1Σ+)) to be mainly available in their electronic ground state, we have only considered electronic states with triplet spin multiplicities. The Cs symmetry of the system was taken into consideration and the first electronic level of each irreducible representation (A′ and A′′) was calculated. The gas-phase chemical reactions investigated in this work, with the respective estimated energies at MRCI-F12/AV(T+d)Z//CAS/AV(T+d)Z + ZPE(CAS/AV(T+d)Z) level, are listed below:
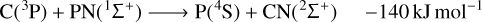 (1)
(1)
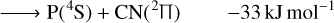 (2)
(2)
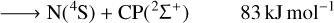 (3)
(3)
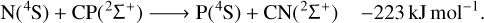 (4)
(4)
The only exoergic products obtained from the C + PN reactants are P + CN. Note that the formation of excited state cyano radical CN(2Π) is also exoergic. The cyano radical has been widely observed in several astronomical environments (McKellar 1940; Adams 1941; Jefferts et al. 1970; Federman et al. 1984; Henkel et al. 1988; Fray et al. 2005; Han et al. 2015; Paron et al. 2021) and one should expect it to be often involved in high energy chemistry. Indeed, from the reactions studied here, CN is not expected to be destroyed by collisions with P (no exoergic products available).
Our calculations also indicate that carbon monophosphide (CP), which has already been detected in space (Guélin et al. 1990), may be promptly destroyed by collisions with neutral N atoms in the highly exoergic N + CP ⟶ P + CN reaction (Eq. (4)). Another possible pathway for CP destruction by N atoms is N + CP ⟶ C + PN (Eq. (3), the reverse of Eq. (3)) with an energy release of −83 kJ mol−1. Our computational results on this reaction corroborates the conclusion of Chantzos et al. (2020) that this reaction may be an important route of PN formation. In addition, Chantzos et al. (2020) also predict that the main formation pathway for PN in the early stage of evolution of diffuse and translucent clouds is P + CN ⟶ C + PN, while according to our calculations this reaction (Eq. (1), the reverse of Eq. (1)) is estimated to be significantly endoergic. Therefore, it should not contribute to PN formation in cold environments such as the ones modelled in the work of Chantzos et al. (2020).
In fact, Chantzos et al. (2020) included the N + CP ⟶ C + PN and P + CN ⟶ C + PN reactions in their chemical network of phosphorus as proposed by Agúndez et al. (2007), which employed a rate coefficient equal to that of the nitrogen analogous reaction (N + CN ⟶ C + N2). The value of k = 3 × 10−10 cm3 s−1 was recommended over the range 300–2500 K and, at low temperatures, the measurements are reported to scatter over four orders of magnitude (Baulch et al. 1992). Moreover, the N + CN ⟶ C + N2 reaction has also been studied computationally (Moskaleva & Lin 2001) and is predicted to be highly exothermic (with an energy release of −205 kJ mol−1), presenting an energy landscape that is very different from that of the true chemical process investigated here. The use of the nitrogen analogous reaction is thus inadequate to properly describe the chemical evolution of these P-bearing species in cold regions of the ISM.
Properties of the asymptotic limits and stationary points of 3A′ and 3A′′ PESs(a).
3.2 Potential energy surface and reaction mechanisms
Along with the thermodynamic analysis presented in the previous section, an investigation of the kinetic viability of the reactions is necessary. The existence of small potential energy barriers, for instance, can turn the formation of thermodynamically favourable products negligible in cold parts of the ISM.
To elucidate the possible reaction pathways of the CPN system, we have explored its triplet A′ and A′′ potential energy surfaces and obtained four relevant potential energy minima and four TSs. Table 1 gathers their geometries and energies, while Fig. 1 shows a potential energy diagram summarising our results and the connections between the stationary structures. The Cartesian coordinates and frequencies of all structures can be found in the supplementary information file.
Starting with the C + PN collision, the ground state for both product channels (P + CN and N + CP) can only be achieved adiabatically in the 3A′′ state (see Fig. 1). The CN radical in its first excited electronic state can also be obtained adiabatically, but on the 3A′ surface. Despite being an exoergic process, it involves surpassing an energy barrier of 42 kJ mol−1 in the entrance channel for the C(3P) + PN(1Σ+) reaction, which should inhibit the formation of excited CN(A2Π) at low temperatures.
It can be seen from Fig. 1 that the relative energies obtained at CCSD(T)-F12 and MRCI-F12 levels are in good agreement, deviating from each other by a maximum of 6 kJ mol−1, except for the TSCPN → CNP and TSCPN → N + CP cases. This may be attributed to a high multiconfigurational character of these structures (the values for the T1 diagnostic is 0.056 and 0.080, respectively). The M06-2X results agree qualitatively with the MRCIF12 ones, with relative energy deviations mostly within 10%. The largest deviation observed in the DFT approach was for the CNP (3A′) minimum, reaching about 22% (an absolute deviation of 30 kJ mol−1). From now on the discussion will be based on the more trustworthy MRCI-F12/AV (T+d)Z//CAS/AV (T+d)Z + ZPE(CAS/AV(T+d)Z) results.
We first address the possible routes of PN destruction by a carbon atom. If the incoming C atom attacks the phosphorus end of the PN molecule, one can notice in Fig. 1 that this can lead to a bent CPN intermediate through a barrierless path on the 3A′′ PES. Subsequently, this minimum can either isomerise to a linear CNP intermediate or dissociate to N(4S) + CP(2Σ+). This abstraction mechanism C + PN ⟶ CPN ⟶ N + CP requires, nevertheless, the surpassing of a 84 kJ mol−1 reaction barrier (relative to C + PN) that separates the CPN minimum from the products. Besides the high energy barrier, the products themselves lie 83 kJ mol−1 above the reactants. Therefore, this mechanism can be considered closed for typical ISM conditions. Furthermore, the isomerisation of the CPN minimum to the CNP one occurs through a conventional TS that lies 40 kJ mol−1 above CPN, but is submerged relatively to reactants. The CNP isomer can also undergo a second isomerisation to yield the linear NCP intermediate, which corresponds to the global minimum of this triatomic system. This second isomerisation also occurs through a conventional TS that is also submerged relatively to reactants. Direct dissociation from the CNP and NCP minima can lead to P(4S) + CN(2Σ+), without an exit barrier. The C+ PN ⟶ P(4 S) + CN(2Σ+) reaction is thus a viable PN destruction route (exoergic and without an activation energy). It is open for whatever temperature, and may be important to model the abundance of PN in the ISM.
The P(4S) + CN(2Σ+) products can also be obtained through a simpler mechanism. For example, by the initial approach of the carbon atom to the diatomic PN via the N atom to form the CNP intermediate, which can then lose the P atom in an overall barrierless process (C+PN ⟶ CNP ⟶ P(4S) + CN(2Σ+)).
In summary, the 3A′′ PES allows for the possibility of several mechanisms of PN destruction by a carbon atom, all of which are listed below:
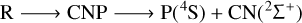 (5)
(5)
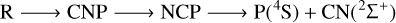 (6)
(6)
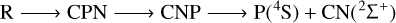 (7)
(7)
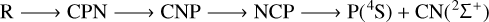 (8)
(8)
where R means reactants (C(3P)+PN(1Σ+)).
When it comes to N + CP collisions, one can see in Fig. 1 that it has two exoergic product channels that may compete: C(3P) + PN(1Σ+) and P(4S) + CN(2Σ+). The abstraction of a carbon atom by the incoming nitrogen atom to produce P(4S) + CN(2Σ+) can easily take place through a direct mechanism that involves the formation of the global minimum of this triatomic system. This N + CP ⟶ NCP ⟶ P(4S) + CN(2Σ+) pathway is barrierless and should be open regardless of the collision energy. The abstraction of the P atom by the incoming N atom to yield C + PN, in turn, presents a small energy barrier in the entrance channel. This barrier of just 1 kJ mol−1 associated with the N + CP ⟶ CPN ⟶ C + PN reaction path lies below the accuracy of our quantum chemical calculations, but this reaction can also occur without an activation energy through the N + CP ⟶ NCP ⟶ CNP ⟶ C + PN mechanism.
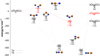 |
Fig. 1 Potential energy diagram for the 3A′ (red) and 3A′′ (black) electronic states of the CPN system. Energies are given in kJ mol−1 relative to the C+PN limit and are ZPE corrected. The MRCI-F12 energies are given in boldface, CCSD(T)-F12 results are given in italics and M06-2X ones are given under parenthesis. Atoms are coloured as: carbon (grey); phosphorus (orange); nitrogen (blue). |
3.3 Reaction rates
Among the reactions addressed in this work, only processes P + CN ⟶ C + PN and N + CP ⟶ C + PN have rate constants available in the UMIST Database for Astrochemistry (UDfA) (McElroy et al. 2013), both having the same value of k = 3 × 10−10 cm3 s−1 and none of them are currently present in KIDA (Wakelam et al. 2012). However, the former reaction is shown here to be endothermic, and the present value available in UDfA may lead to wrong conclusions on astrochemical models. As discussed in Section 3.1, this was estimated based on the analogous nitrogen reaction (N + CN → N2 + C) assuming similar chemical behaviour between the involved species. However, the PN molecule is not as thermodynamically stable as N2, and we have shown that these chemical processes are actually quite different and present very distinct energy landscapes. The P + CN ⟶ C + PN reaction for instance, is significantly endoergic and should not present such a high rate coefficient, nor should it be independent of temperature. As for the N + CP ⟶ C + PN reaction, our calculations predict the existence of a small entrance barrier for the most straightforward mechanism, contrary to what occurs for the analogous nitrogen reaction (Moskaleva & Lin 2001). Therefore, despite being exoergic, one should expect the N + CP ⟶ C + PN reaction to present a lower rate constant than the currently assigned one.
We have used our accurate computations at the MRCI-F12/AV(T+d)Z//CAS/AV(T+d)Z + ZPE(CAS/AV(T+d)Z) level on the CPN system to calculate the rate coefficients of reactions in Eqs. (1), (3), (4) and their reverses as a function of temperature using the MESS package. The rate coefficients obtained for all six reactions for several different temperature values have been fitted to the modified Arrhenius equation:
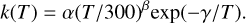 (9)
(9)
and the fitting parameters (α, β and γ constants) are compiled in Table 3. One can also find in this table results from previous studies of our research group as well as the ones proposed by Douglas et al. (2022) and García de la Concepción et al. (2021). In this way, we offer a wide set of reaction rates for modelling the abundances of P-bearing molecules. We also refer the reader to the supplementary information file where one can find more details about the determination of the rate coefficients of the PO + N ⟶ PN + O and PO + N ⟶ NO + P reactions.
The calculated rate coefficients with the respective fitted curves for the exoergic reactions are given in Fig. 2. One can notice that these reactions show a very small temperature dependence, as is usually the case for barrierless exoergic processes. As expected, our predictions that the branching ratio between N + CP ⟶ P + CN and N + CP ⟶ C + PN largely favours the former, although only the latter is available in UDfA. For typical ISM conditions, the difference is about two orders of magnitude.
The obtained rate coefficients for the reaction in Eq. (1), which may have an important impact on the abundance of PN in the ISM as the only reaction able to remove this species through neutral-neutral collision, are shown as blue circles in Fig. 2. They are essentially constant over a wide range of temperatures with a mean value of k = 1.35 × 10−10 cm3 s−1, which is consistent with what is expected from a barrierless exoergic reaction. Nonetheless, a rather unusual increase in the reaction rate coefficients as the temperature decreases can be observed in the low temperature regime (<200 K). This can be explained due to the electronic degeneracy of the carbon atom in the 3P state when we consider the splitting of the ground energy level due to spin-orbit coupling. This interaction gives rise to three finely separated energy levels with total angular momentum quantum number J = 0, 1 and 2 and electronic degeneracy number g = 1, 3 and 5, respectively. As temperature decreases, the states with lower degeneracy (and also lower energy) become more populated, increasing the values of the rate coefficients due to the higher statistical weight factors associated with these states.
The reactions in Eqs. (1) and – (1) have also been approached by Douglas et al. (2022), who essentially set the rate coefficient of the direct process equal to the capture rate calculated using long-range transition state theory (Georgievskii & Klippenstein 2005). The rate constant of the reverse process was then calculated by detailed balance. The authors justify this procedure by considering that the reaction in Eq. (1) does not have a complex PES and they seem to treat only the CNP intermediate as relevant to those reactions, neglecting other possible multistep pathways. It should still be a good approximation and, therefore, they are also shown in Figs. 2 and 3 as dashed lines for comparison. There is clearly good agreement between our results and those obtained by Douglas et al. (2022) for these reactions.
The results for the endoergic reactions are given in Fig. 3 in an Arrhenius plot. The activation energies associated with these processes are related to the slope of the curves. As expected, the rate coefficients of these reactions (Eqs. – (1), (3) and – (4)) present a strong temperature dependence. By analysing the results shown in Fig. 3, it becomes evident that the value assigned in UDfA to the rate constant of the P + CN → C + PN reaction differs drastically to the calculated ones. According to our calculations, only at 1000 K the rate coefficient for the P + CN → C + PN process reaches k = 1.0 × 10−17 cm3 s−1, seven orders of magnitude lower than the temperature independent value based on the analogous N reaction (Baulch et al. 1992; Agúndez et al. 2007). While high-temperature values are relevant for studies of exoplanetary atmospheres (Al-Refaie et al. 2022; Fleury et al. 2025), our focus here is on the relatively cold regions of the ISM. The highest rate coefficient in Fig. 3 is the one of the reaction in Eq. (3), and it only reaches the order of magnitude of 10−10 cm3 s−1 at 7000 K. Hence, we should not expect these endoergic reactions to play a relevant role in the chemical evolution of P-bearing species in cold astronomical environments.
 |
Fig. 2 Rate coefficients as a function of temperature obtained for the exoergic reactions. The points refer to the calculated values at fixed temperatures and the curves correspond to a fit to our results using the modified Arrhenius formula. The rate coefficient proposed by Douglas et al. (2022) for the C + PN ⟶ P + CN reaction is shown as a dashed line for comparison. |
 |
Fig. 3 Rate coefficients as a function of inverse temperature obtained for the endoergic reactions. The points refer to the calculated values at fixed temperatures and the curves correspond to a fit to our results using the modified Arrhenius formula. The rate coefficient proposed by Douglas et al. (2022) for the P + CN ⟶ C + PN reaction is shown as a dashed line for comparison. |
4 Astrochemical modelling of P-bearing species
Evaluating the behaviour of computed reactions in astrochemical models is essential for understanding their impact on the abundances of phosphorus-bearing species. The results are obtained from gas-grain modelling using the Nautilus code, which calculates the initial abundances provided in Table 2 and incorporates the chemical reactions listed in Table 3 into the KIDA network database (see Sect. 2.3). The primary objective is to analyse the temporal evolution of these reactions and predict the abundances of P, PO, PN, and PH (phosphinidene) under conditions that approximate the transition from diffuse to dense cloud environments.
4.1 Diffuse and translucent cloud
In the life cycle of the ISM, diffuse molecular clouds are low density regions primarily composed of molecular hydrogen (H2) and dust, within which translucent clouds are embedded. These clouds play a crucial role in the early stages of star formation, as they provide the necessary environment for the collapse of matter under gravitational forces, eventually leading to the birth of stars. To investigate the formation of P-bearing species in a diffuse molecular environment, we modelled the system under physical conditions with a gas density of 103 cm−3, a standard gas-to-dust ratio mass ratio of 100:1 (Tricco et al. 2017), and a temperature of 70 K (Corby et al. 2018). The initial elemental composition of the gas, including both atoms and ions, is presented in Table 2.
By examining the PO and PN abundances under varying cosmic ray and X-ray ionisation rates, we observed corresponding changes in their ratios. The results are exhibited in Fig. 4, which shows the resultant PO/PN ratios as a function of time for the different models: a), b) and c). It is observed that early in the simulation (t < 102 yr), the impact of the ionisation rates on the ratios is less pronounced. However, as time evolves, the differences in PO/PN ratios among the models become significantly more pronounced. In the final stages (t > 105 yr), the models show PO/PN ratios constrained within an interval of roughly 15 to 60 as the cosmic ray ionisation rates increase from 1.3 × 10−17 s−1 to 1.3 × 10−16 s−1. Higher ionisation rates and energetic phenomena might affect PO chemistry, influencing the abundance of PO relative to PN. This result is consistent with previous studies that combined quantum chemical and kinetic calculations of PO, also evaluating velocity effects within the context of chemical models in shocked regions (García de la Concepción et al. 2021 and references therein). In comparison to other cases, high PO/PN ratios have been observed in comet 67P/Churyumov-Gerasimenko, Rivilla et al. (2020) estimated that PO is significantly more abundant than PN, with PO/PN ratios exceeding 10.
We calculated the abundances of phosphorus-bearing species as a function of time, maintaining the gas temperature and density conditions of the diffuse and translucent cloud described previously. To account for the significance of ionisation rates, we utilised model B to compute the abundances, since it represents an intermediate case with ζCR = 6.3 × 10−17 s−1 and ζX = 5 × 10−18 s−1. The results are shown in Fig. 5, which displays the abundances of P, PO, PN, and the radical PH, over a timescale of 106 yr. The analysis yields key findings, such as the elemental phosphorus remains the most abundant species throughout the simulation. Furthermore, PO consistently exhibits higher abundances than PN. Notably, the predicted abundances of P, PO, PN, and PH (phosphinidene) reach a quasisteady state after approximately 105 years–significantly earlier than the typical chemical age of 106 years, adopted for diffuse molecular clouds (e.g. Albertsson et al. 2014). In this work, we include the results for PH, represented by a dashed line in Fig. 5. Compounds such as phosphinidenes are unstable and highly reactive, presenting a significant challenge for detection. Nevertheless, they play a crucial role in phosphorus chemistry.
Specifically, PH contributes to the formation of both PO and PN through neutral reactions: PH + O ⟶ PO + H and PH + N ⟶ PN + H (Table 3).
 |
Fig. 4 Ratios of PO/PN as a function of time in the diffuse and translucent cloud model: a) ζCR = 1.3 × 10−16 s−1 and ζX = 1 × 10−17 s−1; b) ζCR = 6.3 × 10−17 s−1 and ζX = 5 × 10−18 s−1; and c) ζCR = 1.3 × 10−17 s−1 and ζX = 1 × 10−18 s−1. The dashed line signifies the threshold at which PO/PN equals 1. |
 |
Fig. 5 Evolution of the abundances of P, PO, PN and the radical PH (dashed line) in the diffuse and translucent cloud model, adopting a H2 gas density and temperature of 103 cm−3 and 70 K, respectively, with ζCR = 6.3 × 10−17 s−1 and ζX = 5 × 10−18 s−1. |
4.2 Dense molecular cloud
A second model of phosphorus chemistry was computed under dense cloud conditions. In this context, the final abundances from the diffuse and translucent model become the initial abundances for the dense cloud. Additionally, considering the radiative processes related to gas cooling, we computed the abundances based on a H2 density of 104 cm−3 and a temperature of 30 K. It is important to note that molecular clouds provide effective shielding against ultraviolet and X-ray photons. Consequently, for the dense cloud simulation we adopted AV = 10 mag and utilised the lowest ionisation rates tested in this study, as discussed in Model C, ζCR = 1.3 × 10−17 s−1 and ζX = 1 × 10−18 s−1. Previous research has highlighted the complexities involved in accurately simulating the transitions from low-density, ionised ISM gas to dense, neutral cloud environments (e.g. Phan et al. 2018). Thus, we aim to investigate the phosphorus network with a focus on the following objectives: examining the evolution of abundances, identifying key reaction contributions, analysing implications for steady-state conditions, and the dynamic chemical balance over timescales ranging from 1 × 106 to 1 × 108 yr.
The results of this model are presented in Fig. 6, with the principal contributions of key reactions analysed in Fig. 7. The temporal evolution of the abundances of P, PO, PN, and PH are presented analogously to Fig. 5; however, the analysis is conducted over an extended timescale ranging from 106 to 108 years. This hypothetical prolonged period aims to discuss abundance stabilisation and the dynamics of the chemical network. As shown in Fig. 6, the abundance curves of PO and PN exhibit similar trends, with values fluctuating between ∼ 5 × 10−11 and 5 × 10−8. Except during the initial phase, the model shows that PO maintains a higher abundance than PN throughout the evolution. Consequently, in the final stage, the PO abundance reaches approximately 3.3 × 10−10, whereas the PN abundance, closely resembling that of PH, stabilises around 1.3 × 10−10. Figure 6 also includes the abundance curve of PH, which appears decoupled from the behaviour of PO and PN. The formation of PH is primarily driven by the recombination of molecular ions with electrons, as in reactions like HPO+ + e− ⟶ O + PH and HPN+ + e− ⟶ N + PH. In contrast, its destruction pathways contribute to the synthesis of PO and PN, as seen in the diffuse and translucent model.
We have identified key mechanisms influencing the chemistry of PN and PO. In Fig. 7(a) and (b), we present the percentage contributions of the principal formation and destruction reactions for PN and PO, respectively, as a function of time. In the case of PN (Fig. 7a), it is important to note that its primary formation pathway is attributed to the PO + N reaction, which initially contributes slightly less than 100% and gradually decreases to approximately 50%. Furthermore, the reaction of PH with N contributes to PN formation (e.g. Gomes et al. 2023a), though to a lesser degree. Initially, this pathway contributes for only a minor fraction of the total PN production but gradually increases, reaching approximately 50% in the final stage of the model. Regarding the destruction mechanisms, PN is primarily destroyed through two pathways involving reactions with H+ and C, with the latter being one of the major reactions explored in this work. The curves associated with these mechanisms exhibit a degree of symmetry, which may arise from the complex interactions inherent in the computations performed by the code. This symmetry indicates a certain predictability and alternation; for instance, at t ≈ 1.5 × 107 yr it can be observed that the contribution of H+ to PN destruction diminishes as the contribution from C becomes more significant.
In the analysis of major reactions influencing PO abundance (Fig. 7b), the primary formation mechanism is the reaction between P and OH (e.g. García de la Concepción et al. 2021), which initially accounts for ∼ 88% of the PO production. However, as the chemical network evolves, its contribution gradually decreases towards the final stage of the model. In contrast, the PH + O reaction follows an opposite trends, since it begins with a minimal contribution but steadily increases. As a result, the contribution profiles of these two pathways shift over time, intersecting at approximately t = 6 × 106 yr. To a lesser extent, the reaction HPO+ + e− also contributes to the PO production, though their impact is significantly lower than that of the P + OH and PO + H pathways. Regarding the major destruction pathways of PO, two key reactions contribute to its depletion: PO + N and PO + H+. The relative significance of these mechanisms evolves over time. Initially, the PO + N reaction is the dominant process; however, its contribution gradually declines, allowing the PO + H+ reaction to become the primary destruction pathway in the later stages.
Our findings indicate that the computed kinetic equations and percentage contributions reveal a pattern that is both somewhat predictable and alternates in behaviour. The formation routes (P + OH and PH + O) appear to establish a dynamic equilibrium with the destruction mechanisms (PO + N and PO + H+), suggesting that the steady-state abundance of PO is regulated by the competition between these pathways, which in turn has an effect on the chemistry and abundance of PN. In future work, we will explore this equilibrium in greater detail, assessing its implications for the predictability of chemical abundances under interstellar conditions.
 |
Fig. 6 Similar to Fig. 5, depicting a stage from 106 yr to 108 yr for a dense cloud model. The parameters are set to a temperature of 30 K, a H2 density of 104 cm−3 and adopting ζCR = 1.3 × 10−17 s−1 and ζX = 1 × 10−18 s−1. |
 |
Fig. 7 Major reactions for a) PN and b) PO. The contributions of each reaction are represented as percentages over time. Solid and dashed lines differentiate production and destruction mechanisms, respectively. The time is presented on a logarithmic scale to highlight contributions beyond 106 years, with a horizontal grey line at 50% for assessing balance throughout the duration of the long-term trends in the chemical network. |
5 PO/PN ratios and observational implications
PO and PN have been identified across a range of astronomical environments, including star-forming regions, protostellar objects, shock regions, and giant molecular clouds. Generally, these molecules have been observed in the interstellar medium and within the circumstellar envelopes of evolved stars. Among the two species, PO is widely recognised as being both more abundant and more prevalent than PN. Studies in the literature consistently indicate that PO is typically more abundant than PN by factors of approximately 1.4 to 3, regardless of the specific physical characteristics of the observed sources (Fernández-Ruz et al. 2023). In modelling a diffuse and translucent cloud, we consistently found that PO is more abundant than PN, with both species displaying a dependence on factors such as visual extinction and influenced by factors like X-ray and cosmic ray ionisation rates. Specifically, these findings suggest that the PO/PN ratios vary over time and increase as the cosmic ray ionisation rate rises from ζCR = 1.3 × 10−17 to 1.3 × 10−16 s−1. However, under conditions of low ionisation rates, the PO/PN ratio may drop below 1. This fluctuation highlights the sensitivity of phosphorus chemistry to ionisation mechanisms, emphasising its critical role in modelling the relative abundances of PO and PN over time.
In a study of diffuse and translucent clouds, Chantzos et al. (2020) conducted observations along the line of sight towards B0355+508, focusing on the analysis of P-bearing species. For PO and PN, the derived upper abundance limits were determined to be <5.0 × 10−10 and <4.9 × 10−11, respectively. Based on our theoretical predictions (Fig. 5), we estimate PO and PN abundances reaching ∼ 1 × 10−10 and 2 × 10−12, respectively, which are consistent with these upper limits. In a study of P-bearing species on a galactic scale, Koelemay et al. (2023) determined the abundances of PO and PN in a star-forming region in the outer Galaxy to be ∼ 2.0 × 10−11 and 3.0 × 10−12, respectively. They also estimated a fit for the PO and PN abundances as a function of distance from the Galactic Centre, suggesting a slight gradient–a decrease in abundance by factors of approximately 1.5 and 2.3 for PO and PN, respectively, between 8.5 and 22.6 kpc.
In a model simulating the conditions of a denser cloud (n ≃ 104 cm−3), adopting the standard cosmic ray ionisation rate (ζCR = 1.3 × 10−17 s−1), we predicted the abundances of P, PO, PN, and PH, along with the major reaction pathways involving these species. In this model, the final abundances of PO and PN were estimated to be ∼ 3 × 10−10 and 1 × 10−10, respectively. Through a detailed examination of the chemical reactions involving both species, we identified that the primary formation pathway of PN occurs via the reaction of PO with N. This finding is further supported by recognising that the primary mechanism for PO destruction is its reaction with N, which leads to PN formation (see Fig. 7). In an early work, Thorne et al. (1984), using laboratory results and kinetic modelling, highlighted the significance of PO as a pivotal species in phosphorus chemistry, serving as a primary reservoir of phosphorus with the potential for other species, such as PN and CP. Consequently, PO is a molecule that, once synthesised, accumulates in sufficient quantities to support the formation of additional species, such as PN, without being considerably depleted.
Bernal et al. (2021) reported relative abundances of PO ∼ 1.6 × 10−10 and PN ∼ 6.1 × 10−11 in the Orion Plateau, yielding a PO/PN ratio of approximately 3. They discussed the presence of PO in high-mass star-forming regions, with the potential for its occurrence in low-mass sources as well. In the Orion-KL region, the clear association between PO and PN suggests that these two molecules are likely formed together through interconnected reactions, as it has been found in the present work. In the context of solar-type protostellar objects, the shock region L1157-B1 is characterised by active and complex chemistry. The detection and formation of various molecules, including HCN, HNC, SiS, HC3N, PO and PN, have been investigated in detail, with a particular focus on shock-induced gas-phase chemistry (Lefloch et al. 2016; Mendoza et al. 2018; Mota et al. 2021; Lefloch et al. 2021). In a recent study, Lefloch et al. (2024) reported that the PO/PN abundance ratios range from 1 to 5. They argued that the PO/PN ratios observed throughout B1 indicate that the phosphorous chemistry is time-dependent. It has also been suggested that neither species is sputtered from icy mantles; rather, PO forms in the gas phase, followed by the subsequent synthesis of PN (see also Lefloch et al. 2016). García de la Concepción et al. (2021) carried out quantum chemical computations to determine the reaction rates and branching ratios for the reactions P + OH → PO + H and P + H2O → PO + H2. Additionally, they conducted chemical modelling in a shocked region, predicting PO/PN ratios exceeding 1, ranging from 3 to 9. Wurmser & Bergner (2022) conducted a search for PN and PO lines towards a sample of solar-type protostars with well-characterised outflows. They identified a relatively narrow range of PO/PN ratios, extending from 0.6 to 2.2. Their analysis highlighted the critical role of outflows and shocked gas in driving gas-phase phosphorus chemistry in these types of sources. Consistent with findings in the literature, gas-phase phosphorus reactions account for the observed abundances of species such as PO and PN. However, follow-up studies are essential to investigate the chemical dynamics between PO and PN in greater detail, as these species play a fundamental role in complex processes related to prebiotic chemistry and astrobiology.
6 Conclusions
Current astrochemical models lack important PN destruction routes (Fernández-Ruz et al. 2023). Furthermore, reactions such as N + CP → PN + C and P + CN → PN + C have very uncertain rate constants available in the literature (Jiménez-Serra et al. 2018), and the rate coefficient of the nitrogen analogous reaction (N + CN → N2 + C) is often used to describe the chemical evolution of these P-bearing molecules in the interstellar medium (Fernández-Ruz et al. 2023). In this work we tackled these issues by performing high-accuracy theoretical calculations (MRCI-F12/AV(T+d)Z//CAS/AV(T+d)Z and CCSD(T)-F12/VTZ-F12//M06-2X/AV(T+d)Z) and employing transition state theory to study the potential energy landscape of the CPN system and to elucidate the kinetics of the C(3P) + PN(1Σ+) destruction of phosphorus nitride. The outcomes of collisions involving N(4S) + CP(2Σ+) and P(4S) + CN(2Σ+) species were also investigated. We have then integrated a revised chemical network for P-bearing molecules into the default KIDA network and ran the Nautilus gas-grain Astrochemical code to investigate the temporal evolution of these reactions within diffuse and dense interstellar cloud conditions.
We have found several mechanisms for PN destruction by collisions with a carbon atom that can lead to P(4S) + CN(2Σ+) formation without an activation barrier. This is the only product channel that is open for the C(3P) + PN(1Σ+) reaction for whatever collision energy. Regarding the kinetics, the temperature-dependent rate coefficients for the reactions addressed in this work were fitted to the modified Arrhenius equation: k(T) = α(T/300)β exp (−γ/T). The C(3P) + PN(1Σ+) → P(4S) + CN(2Σ+) reaction has a rate coefficient with parameters α = 1.29 × 10−10 cm3 s−1, β = 0.025 and γ = −10.0 K, consisting in a relevant PN destruction route that should be important to properly model the abundances of P-bearing species in the ISM.
The N(4S) + CP(2Σ+) formation processes were found to be considerably endoergic and mechanisms towards CP formation should not take place unless very high temperatures are involved. The destruction of CP, however, is expected to readily occur by collisions with nitrogen atoms even at low temperatures. The obtained rate coefficient for the N(4S) + CP(2Σ+) → P(4S) + CN(2Σ+) reaction has α = 1.74 × 10−10 cm3 s−1, β = 0.172 and γ = 0 and is higher than the one obtained for the N(4S) + CP(2Σ+) → C(3P) + PN(1Σ+), which has α = 9.86 × 10−12 cm3 s−1, β = 0.634 and γ = 0. To the best of our knowledge, both rate constants are being reported for the first time. We have also concluded that the energy landscape of the CPN system is very different from that of NCN, and the use of the rate coefficient of the nitrogen analogous reaction is not adequate to describe the evolution of reactions within the CPN system.
We have presented two chemical models to predict the abundances of phosphorus-bearing species, specifically P, PO, PN, and PH, under varying astrophysical conditions. In the diffuse cloud scenario, the influence of ionising agents on phosphorus chemistry was investigated through PO/PN abundance ratios. Our results indicate that models with higher X-ray and cosmic ray ionisation rates strongly favour PO formation, leading to PO/PN ratios significantly greater than 1. In contrast, models with lower ionisation rates can result in slightly higher PN abundances, with PO/PN approaching or slightly below 1 around t = 103 yr. In the final phase of the model (t ≈ 1 × 106 yr), PO/PN range from 15 to 60 depending on the ionisation rates. A diffuse cloud model was computed for an intermediate ionisation rate scenario, assuming ζCR = 6.3 × 10−17 s−1 and ζX = 5 × 10−18 s−1. As a result, quasi-stable abundances of PO and PN were obtained for t > 105 yr, with values of ≈ 1 × 10−10 and ≈ 2 × 10−12, respectively.
For a subsequent second model adopting dense cloud conditions, the chemical network was computed over an extended hypothetical time-scale ranging from 106 to 108 yr, with ζCR = 1.3 × 10−17 s−1 and ζX = 1 × 10−18 s−1. The results indicate that PO and PN abundances slightly fluctuate over time, with values ranging from 5 × 10−11 to 5 × 10−8. The balance of the chemical network and its influence on steady-state abundances were analysed by examining the temporal percentage contributions of key reactions. PO is consistently the most abundant species compared to PN and PH under these conditions. A detailed analysis of the key formation and destruction pathways revealed that PO is primary produced via the P + OH and PH + O reactions, whose relative contributions vary over time. With a lower contribution (up to 20%), the HPO+ + e− reaction also plays a role in the PO formation. Regarding PO destruction mechanisms, the most significant channels are PO + N and PO + H+. An analysis of the major formation and destruction pathways of PN was carried out. The primary formation of PN occurs via the reaction of PO with N, contributing more than 50%. This underscores the critical role of PO as a reservoir species that accumulates sufficiently to drive subsequent PN formation. Nevertheless, PO remains as the most abundant P-bearing molecule. The second most important mechanism, the PH + N reaction, contributes to the remaining percentage. Finally, regarding PN destruction, we find that its depletion is primarily driven by reactions with H+ and C. These findings align with earlier studies, confirming the interplay of phosphorus chemistry under varying ionisation environments.
In future work, we intend to further enhance the accuracy of the obtained rate coefficients for the approached chemical reactions by performing quasi-classical trajectory simulations. It involves, however, the calculation of a huge set of ab initio energies for sufficiently many nuclear arrangements so that an analytic expression can be fitted to such data and used to model the interaction potential. Despite being a very timeconsuming process, a reliable analytical model offers the advantage of providing fast, continuous and differentiable representations of the PES (Rocha & Varandas 2020). A robust scheme, called the Combined-Hyperbolic-Inverse-Power-Representation (CHIPR) method, has been proposed by Varandas (Varandas 2013a,b), and the code of a general program for analytically representing PESs of any triatomic molecules with CHIPR has already been provided (Rocha & Varandas 2020). This method should be used as the next step in our study of the CPN system.
Data availability
The data underlying this article are available in the article and in its online supplementary material at https://doi.org/10.5281/zenodo.15002910
Acknowledgements
We would like to thank the anonymous reviewer for their insightful comments. The authors would like to thank the financial support provided by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES, finance code 001), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, grants 311508-2021-9 and 405524-2021-8), Fundação de Amparo à Pesquisa e Inovação do Espírito Santo (FAPES), Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG, grants APQ-03705-23 and RED-00045-23), Centro Federal de Educação Tecnológica de Minas Gerais (CEFET-MG) and Universidade Federal do Espírito Santo (UFES). E.M. acknowledges support under the grant “María Zambrano” from the UHU funded by the Spanish Ministry of Universities and the “European Union NextGenerationEU.” This project has also received funding from the European Union’s Horizon 2020 research and innovation program under Marie Sklodowska-Curie grant agreement No. 872081, and grant PID2022-136228NBC21 (M.C.) funded by MCIN/AEI/10.13039/501100011033, and, as appropriate, by “ERDF A way of making Europe”, the “European Union”, or the “European Union NextGenerationEU/PRTR”. This work is also supported by the Consejería de Transformación Económica, Industria, Conocimiento y Universidades, Junta de Andalucía and European Regional Development Fund (ERDF 2021-2027) under the project EPIT1462023 (M.C. and E.M.).
References
- Adams, W. S. 1941, ApJ, 93, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Adler, T. B., Knizia, G., & Werner, H.-J. 2007, J. Chem. Phys., 127, 221106 [Google Scholar]
- Agúndez, M., Cernicharo, J., & Guélin, M. 2007, ApJ, 662, L91 [CrossRef] [Google Scholar]
- Agúndez, M., Cernicharo, J., & Guélin, M. 2014a, A&A, 570, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agúndez, M., Cernicharo, J., Decin, L., Encrenaz, P., & Teyssier, D. 2014b, ApJ, 790, L27 [Google Scholar]
- Albertsson, T., Indriolo, N., Kreckel, H., et al. 2014, ApJ, 787, 44 [Google Scholar]
- Al-Refaie, A. F., Changeat, Q., Venot, O., Waldmann, I. P., & Tinetti, G. 2022, ApJ, 932, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Altwegg, K., Balsiger, H., Bar-Nun, A., et al. 2016, SciA, 2, e1600285 [Google Scholar]
- Baulch, D. L., Cobos, C. J., Cox, R. A., et al. 1992, JPCRD, 21, 411 [NASA ADS] [Google Scholar]
- Bergner, J. B., Öberg, K. I., Walker, S., et al. 2019, ApJ, 884, L36 [CrossRef] [Google Scholar]
- Bernal, J. J., Koelemay, L. A., & Ziurys, L. M. 2021, ApJ, 906, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Bode, B. M., & Gordon, M. S. 1998, J. Mol. Graph. Mod., 16, 133 [Google Scholar]
- Bregman, J. D., Lester, D. F., & Rank, D. M. 1975, ApJ, 202, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Campanha, D. R., Mendoza, E., Silva, M. X., et al. 2022, MNRAS, 515, 369 [CrossRef] [Google Scholar]
- Chantzos, J., Rivilla, V. M., Vasyunin, A., et al. 2020, A&A, 633, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chesnavich, W. J. 1986, J. Chem. Phys., 84, 2615 [NASA ADS] [CrossRef] [Google Scholar]
- Corby, J. F., McGuire, B. A., Herbst, E., & Remijan, A. J. 2018, A&A, 610, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalgarno, A. 2006, PNAS, 103, 12269 [NASA ADS] [CrossRef] [Google Scholar]
- De Beck, E., Kamiński, T., Patel, N. A., et al. 2013, A&A, 558, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Douglas, K. M., Gobrecht, D., & Plane, J. M. C. 2022, MNRAS, 515, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Dufour, G., Charnley, S. B., & Lindberg, J. E. 2023, MNRAS, 520, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Dunning, T. H. J. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Eckart, C. 1930, Phys. Rev., 35, 1303 [Google Scholar]
- Federman, S. R., Danks, A. C., & Lambert, D. L. 1984, ApJ, 287, 219 [Google Scholar]
- Fernández-García, C., Coggins, A. J., & Powner, M. W. 2017, Life, 7, 31 [Google Scholar]
- Fernández-Ruz, M., Jiménez-Serra, I., & Aguirre, J. 2023, ApJ, 956, 47 [CrossRef] [Google Scholar]
- Fleury, B., Poveda, M., Benilan, Y., et al. 2025, A&A, 693, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Rivilla, V. M., Caselli, P., Vasyunin, A., & Palau, A. 2016, ApJ, 822, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Fontani, F., Rivilla, V. M., van der Tak, F. F. S., et al. 2019, MNRAS, 489, 4530 [CrossRef] [Google Scholar]
- Francisco, J. S. 2003, Chem. Phys., 287, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Fray, N., Bénilan, Y., Cottin, H., Gazeau, M.-C., & Crovisier, J. 2005, Planet. Space Sci., 53, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- García de la Concepción, J., Puzzarini, C., Barone, V., Jiménez-Serra, I., & Roncero, O. 2021, ApJ, 922, 169 [CrossRef] [Google Scholar]
- García de la Concepción, J., Cavallotti, C., Barone, V., Puzzarini, C., & JiménezSerra, I. 2024, ApJ, 963, 142 [Google Scholar]
- Georgievskii, Y., & Klippenstein, S. J. 2005, J. Chem. Phys., 122, 194103 [Google Scholar]
- Georgievskii, Y., Miller, J. A., Burke, M. P., & Klippenstein, S. J. 2013, J. Phys. Chem. A, 117, 12146 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, A. C. R., Rocha, C. M. R., Jasper, A. W., & Galvão, B. R. L. 2022, J. Mol. Model., 28, 259 [Google Scholar]
- Gomes, A. C. R., Souza, A. C., Jasper, A. W., & Galvão, B. R. L. 2023a, PASA, 40, e011 [Google Scholar]
- Gomes, A. C. R., Spada, R. F. K., Lefloch, B., & Galvão, B. R. L. 2023b, MNRAS, 518, 5991 [Google Scholar]
- Goto, M., Geballe, T. R., Indriolo, N., et al. 2014, ApJ, 786, 96 [CrossRef] [Google Scholar]
- Guélin, M., Cernicharo, J., Paubert, G., & Turner, B. E. 1990, A&A, 230, L9 [NASA ADS] [Google Scholar]
- Haasler, D., Rivilla, V. M., Martín, S., et al. 2022, A&A, 659, A158 [CrossRef] [EDP Sciences] [Google Scholar]
- Halfen, D. T., Clouthier, D. J., & Ziurys, L. M. 2008, ApJ, 677, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Han, X. H., Zhou, J. J., Wang, J. Z., et al. 2015, A&A, 576, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanwell, M. D., Curtis, D. E., Lonie, D. C., et al. 2012, J. Cheminform., 4, 1 [Google Scholar]
- Henkel, C., Mauersberger, R., & Schilke, P. 1988, A&A, 201, L23 [Google Scholar]
- Hunter, T. 2012, Philos. Trans. R. Soc. B., 367, 2513 [Google Scholar]
- Jefferts, K. B., Penzias, A. A., & Wilson, R. W. 1970, ApJ, 161, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [Google Scholar]
- Jiménez-Serra, I., Viti, S., Quénard, D., & Holdship, J. 2018, ApJ, 862, 128 [CrossRef] [Google Scholar]
- Kendall, R. A., Dunning, T. H. J., & Harrison, R. J. 1992, J. Chem. Phys., 96, 6796 [NASA ADS] [CrossRef] [Google Scholar]
- Knizia, G., Adler, T. B., & Werner, H.-J. 2009, J. Chem. Phys., 130, 054104 [Google Scholar]
- Koelemay, L. A., Gold, K. R., & Ziurys, L. M. 2023, Nature, 623, 292 [Google Scholar]
- Kohn, W., & Sham, L. J. 1965, Phys. Rev., 140, A1133 [CrossRef] [Google Scholar]
- Larson, H. P., Treffers, R. R., & Fink, U. 1977, ApJ, 211, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, T. J. 2003, Chem. Phys. Lett., 372, 362 [Google Scholar]
- Lee, T. J., & Taylor, P. R. 1989, Int. J. Quant. Chem., 36, 199 [Google Scholar]
- Lefloch, B., Vastel, C., et al. 2016, MNRAS, 462, 3937 [CrossRef] [Google Scholar]
- Lefloch, B., Busquet, G., Viti, S., et al. 2021, MNRAS, 507, 1034 [CrossRef] [Google Scholar]
- Lefloch, B., Codella, C., Montargès, M., et al. 2024, A&A, 687, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leininger, M. L., Nielsen, I. M., Crawford, T., & Janssen, C. L. 2000, Chem. Phys. Lett., 328, 431 [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKellar, A. 1940, PASP, 52, 187 [Google Scholar]
- Mendoza, E., Lefloch, B., Ceccarelli, C., et al. 2018, MNRAS, 475, 5501 [NASA ADS] [CrossRef] [Google Scholar]
- Milam, S. N., Halfen, D. T., Tenenbaum, E. D., et al. 2008, ApJ, 684, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J., Bennett, A., & Herbst, E. 1987, MNRAS, 229, 41 [Google Scholar]
- Mininni, C., Fontani, F., Rivilla, V. M., et al. 2018, MNRAS, 476, L39 [CrossRef] [Google Scholar]
- Montgomery, J. A., J., Frisch, M. J., Ochterski, J. W., & Petersson, G. A. 2000, J. Chem. Phys., 112, 6532 [NASA ADS] [CrossRef] [Google Scholar]
- Moskaleva, L. V., & Lin, M. C. 2001, J. Phys. Chem. A, 105, 4156 [Google Scholar]
- Mota, V. C., Varandas, A. J. C., Mendoza, E., Wakelam, V., & Galvão, B. R. L. 2021, ApJ, 920, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Notsu, S., van Dishoeck, E. F., Walsh, C., Bosman, A. D., & Nomura, H. 2021, A&A, 650, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paron, S., Ortega, M. E., Marinelli, A., Areal, M. B., & Martinez, N. C. 2021, A&A, 653, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasek, M. A., & Lauretta, D. S. 2005, Astrobiology, 5, 515 [Google Scholar]
- Pechukas, P., & Light, J. C. 1965, J. Chem. Phys., 42, 3281 [NASA ADS] [CrossRef] [Google Scholar]
- Phan, V. H. M., Morlino, G., & Gabici, S. 2018, MNRAS, 480, 5167 [NASA ADS] [Google Scholar]
- Plane, J. M. C., Feng, W., & Douglas, K. M. 2021, J. Geophys. Res. Space Phys., 126, e2021JA029881 [Google Scholar]
- Puzzarini, C. 2006, J. Mol. Struct., 780, 238 [Google Scholar]
- Rivilla, V. M., Fontani, F., Beltrán, M. T., et al. 2016, ApJ, 826, 161 [CrossRef] [Google Scholar]
- Rivilla, V. M., Jiménez-Serra, I., Zeng, S., et al. 2018, MNRAS, 475, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Rivilla, V. M., Drozdovskaya, M. N., Altwegg, K., et al. 2020, MNRAS, 492, 1180 [Google Scholar]
- Rocha, C., & Varandas, A. 2020, Comput. Phys. Commun., 247, 106913 [Google Scholar]
- Roueff, E., & Le Bourlot, J. 2020, A&A, 643, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruaud, M., Wakelam, V., & Hersant, F. 2016, MNRAS, 459, 3756 [Google Scholar]
- Ruaud, M., Wakelam, V., Gratier, P., & Bonnell, I. A. 2018, A&A, 611, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwartz, A. W. 2006, Phil. Trans. R. Soc. B, 361, 1743 [Google Scholar]
- Shiozaki, T., Knizia, G., & Werner, H.-J. 2011, J. Chem. Phys., 134, 034113 [NASA ADS] [CrossRef] [Google Scholar]
- Sil, M., Srivastav, S., Bhat, B., et al. 2021, AJ, 162, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Souza, A. C., Silva, M. X., & Galvão, B. R. L. 2021, MNRAS, 507, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Stäuber, P., Doty, S. D., van Dishoeck, E. F., & Benz, A. O. 2005, A&A, 440, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szalay, P. G., Müller, T., Gidofalvi, G., Lischka, H., & Shepard, R. 2012, Chem. Rev., 112, 108 [Google Scholar]
- Tenenbaum, E. D., Woolf, N. J., & Ziurys, L. M. 2007, ApJ, 666, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Thorne, L. R., Anicich, V. G., Prasad, S. S., & Jr, W. T. H. 1984, ApJ, 280, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Tricco, T. S., Price, D. J., & Laibe, G. 2017, MNRAS, 471, L52 [Google Scholar]
- Turner, B. E., & Bally, J. 1987, ApJ, 321, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Varandas, A. J. C. 2013a, J. Chem. Phys., 138, 054120 [Google Scholar]
- Varandas, A. J. C. 2013b, in Reaction Rate Constant Computations: Theories and Applications (The Royal Society of Chemistry) [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [Google Scholar]
- Wakelam, V., Loison, J. C., Herbst, E., et al. 2015, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Gratier, P., Loison, J. C., et al. 2024, A&A, 689, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, H.-J., Knowles, P. J., Knizia, G., et al. 2015, MOLPRO, version 2015.1, a package of ab initio programs [Google Scholar]
- Wolfire, M. G., Vallini, L., & Chevance, M. 2022, ARA&A, 60, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Wurmser, S., & Bergner, J. B. 2022, ApJ, 934, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Yamaguchi, T., Takano, S., Sakai, N., et al. 2011, PASJ, 63, L37 [NASA ADS] [Google Scholar]
- Zhao, Y., & Truhlar, D. G. 2008, Theor. Chem. Account., 120, 215 [Google Scholar]
- Ziurys, L. M. 1987, ApJ, 321, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L. M., Schmidt, D. R., & Bernal, J. J. 2018, ApJ, 856, 169 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Properties of the asymptotic limits and stationary points of 3A′ and 3A′′ PESs(a).
All Figures
 |
Fig. 1 Potential energy diagram for the 3A′ (red) and 3A′′ (black) electronic states of the CPN system. Energies are given in kJ mol−1 relative to the C+PN limit and are ZPE corrected. The MRCI-F12 energies are given in boldface, CCSD(T)-F12 results are given in italics and M06-2X ones are given under parenthesis. Atoms are coloured as: carbon (grey); phosphorus (orange); nitrogen (blue). |
| In the text | |
 |
Fig. 2 Rate coefficients as a function of temperature obtained for the exoergic reactions. The points refer to the calculated values at fixed temperatures and the curves correspond to a fit to our results using the modified Arrhenius formula. The rate coefficient proposed by Douglas et al. (2022) for the C + PN ⟶ P + CN reaction is shown as a dashed line for comparison. |
| In the text | |
 |
Fig. 3 Rate coefficients as a function of inverse temperature obtained for the endoergic reactions. The points refer to the calculated values at fixed temperatures and the curves correspond to a fit to our results using the modified Arrhenius formula. The rate coefficient proposed by Douglas et al. (2022) for the P + CN ⟶ C + PN reaction is shown as a dashed line for comparison. |
| In the text | |
 |
Fig. 4 Ratios of PO/PN as a function of time in the diffuse and translucent cloud model: a) ζCR = 1.3 × 10−16 s−1 and ζX = 1 × 10−17 s−1; b) ζCR = 6.3 × 10−17 s−1 and ζX = 5 × 10−18 s−1; and c) ζCR = 1.3 × 10−17 s−1 and ζX = 1 × 10−18 s−1. The dashed line signifies the threshold at which PO/PN equals 1. |
| In the text | |
 |
Fig. 5 Evolution of the abundances of P, PO, PN and the radical PH (dashed line) in the diffuse and translucent cloud model, adopting a H2 gas density and temperature of 103 cm−3 and 70 K, respectively, with ζCR = 6.3 × 10−17 s−1 and ζX = 5 × 10−18 s−1. |
| In the text | |
 |
Fig. 6 Similar to Fig. 5, depicting a stage from 106 yr to 108 yr for a dense cloud model. The parameters are set to a temperature of 30 K, a H2 density of 104 cm−3 and adopting ζCR = 1.3 × 10−17 s−1 and ζX = 1 × 10−18 s−1. |
| In the text | |
 |
Fig. 7 Major reactions for a) PN and b) PO. The contributions of each reaction are represented as percentages over time. Solid and dashed lines differentiate production and destruction mechanisms, respectively. The time is presented on a logarithmic scale to highlight contributions beyond 106 years, with a horizontal grey line at 50% for assessing balance throughout the duration of the long-term trends in the chemical network. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


