| Issue |
A&A
Volume 694, February 2025
|
|
|---|---|---|
| Article Number | A244 | |
| Number of page(s) | 6 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202453017 | |
| Published online | 18 February 2025 | |
Gamma rays from star clusters and implications for the origin of Galactic cosmic rays
1
GSSI – Gran Sasso Science Institute,
Viale F. Crispi 7,
67100
L’ Aquila,
Italy
2
INFN – Laboratori Nazionali del Gran Sasso,
Via G. Acitelli 22,
Assergi (AQ),
Italy
★ Corresponding author; pasquale.blasi@gssi.it
Received:
15
November
2024
Accepted:
23
January
2025
Context. Star clusters are often invoked as contributors to the flux of Galactic cosmic rays and as sources potentially able to accelerate particles to ∼Peta-electronVolt energies. The gamma radiation with E ≳ 1 TeV recently observed from selected star clusters has profound implications for the origin of Galactic cosmic rays.
Aims. We show that if the gamma rays observed from the Cygnus cocoon and Westerlund 1 are of hadronic origin, then the cosmic rays escaping the cluster at energies ≳10 TeV must cross a grammage inside the cluster that exceeds the Galactic grammage. At lower energies, depending on the model adopted to describe the production of gamma rays, such grammage may exceed or be comparable with the grammage inferred from propagation on Galactic scales.
Methods. We analytically computed the flux of gamma rays for a few models of injection of cosmic rays in star clusters and compared it with the flux measured from selected clusters.
Results. In all the models considered here, comparing the inferred and observed gamma ray fluxes at E ≳ 1 TeV, we conclude that CRs must traverse a large grammage inside or around the cluster before escaping. Clearly these implications would not apply to a scenario in which gamma rays are produced due to radiative losses of leptons in the cluster. Leptonic models typically require weaker magnetic fields, which in turn result in maximum energies of accelerated particles much below ∼1 PeV.
Conclusions. We conclude that if gamma ray emission in SCs is a generic phenomenon and if this radiation is due to hadronic interactions, either star clusters cannot contribute but a small fraction of the total cosmic ray flux at the Earth or their contribution to the grammage cannot be neglected, and the paradigm of Galactic transport should be profoundly revisited.
Key words: acceleration of particles / astroparticle physics / cosmic rays / gamma rays: stars
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Star clusters (SCs) have long been proposed as possible sources contributing to the Galactic cosmic ray (CR) flux. The interest in such sources is mainly due to the fact that SCs might host the right conditions for the acceleration of CRs up to the knee and provide an explanation of the well-known 22Ne/20Ne excess in CRs (Gupta et al. 2020).
Particle acceleration could occur at the termination shock of the collective wind launched by the young stars located in the cluster core, if the SC is sufficiently compact (Morlino et al. 2021; Blasi & Morlino 2023), or occur due to supernova explosions (Vieu et al. 2022), for sufficiently old SCs. Second order Fermi acceleration in the bubble has also been invoked as a possible mechanism of particle acceleration (Vink 2024). The maximum energy that can be achieved at the termination shock depends rather crucially on details of CR transport in the bubble. For instance, as discussed by Morlino et al. (2021); Blasi & Morlino (2023), although a formal estimate of the maximum energy, Emax, attainable at the termination shock can easily approach ~Peta-electronVolt, the spherical symmetry of the problem introduces a curvature in the spectrum of accelerated particles that starts at energies much lower than Emax. The only exception to this conclusion is the case of Bohm diffusion, but it is unlikely to apply to the case of extrinsic turbulence.
From the observational point of view, gamma ray telescopes such as the High-Altitude Water Cherenkov Observatory (HAWC) (Abeysekara et al. 2021) and the Large High Altitude Air Shower Observatory (LHAASO) (Cao et al. 2021) have measured the flux of gamma rays from selected SCs, and the spectrum appears to drop appreciably at energies much lower than Peta-ElectronVolt despite the fact that photons with energy as high as 2.5 PeV have recently been detected by LHAASO from a region of ~6° in the direction of the Cygnus OB association (Lhaaso Collaboration 2024). Gamma ray emission has now been detected from a number of SCs, such as Westerlund 1 (Abramowski et al. 2012), Westerlund 2 (Yang et al. 2018), the Cygnus cocoon (Ackermann et al. 2011; Aharonian et al. 2019), NGC 3603 (Saha et al. 2020), BDS2003 (Albert et al. 2021), W40 (Sun et al. 2020), and 30 Doradus in the Large Magellanic Cloud (H. E. S. S. Collaboration 2015). Several very young SCs have also been detected in gamma rays in the ≲100 GeV energy range (Peron et al. 2024a).
Detailed calculations of particle acceleration and transport in the bubble excavated by the wind carried out by Blasi & Morlino (2023) (see also Menchiari (2023)) and the more phenomenological estimates presented in Cao et al. (2021) suggest that in order to account for the level of gamma ray emission in the Cygnus SC, a mean density of ~5–10 cm–3 is needed in the bubble. Such gas is not the diffuse gas associated with the collective wind of the SC, which has a much lower density, typically ~10–3 cm–3. The mean density should rather be dominated by atomic and molecular gas clumped in dense regions with a larger local density. Such clumps can either be the leftover of the passage of the shock associated with the collective wind or formed as a result of the cooling of the gas plowed away toward the outer edge of the bubble. Accepting the presence of this gas and attributing the gamma ray emission to hadronic interactions with such gas, Blasi & Morlino (2024) showed that the spectra of H and He nuclei escaping the SC are different, which is in agreement with what was inferred from CR data collected by the CREAM collaboration (Ahn et al. 2010), by PAMELA (Adriani et al. 2011), AMS-02 (Aguilar et al. 2015b,a), DAMPE (An et al. 2019; Ale- manno et al. 2021), and CALET (Adriani et al. 2022, 2023). The disappointing by-product of this finding is that, in this case, heavier nuclei are severely depleted due to spallation inside the bubble, so SCs cannot contribute an appreciable flux of nuclei heavier than He.
This was the first symptom of a more general implication of the detection of gamma rays from Cygnus and other clusters: if of hadronic origin, this radiation forces us to conclude that CRs in SCs need to cross a large grammage inside the bubble. For the reference values of the mean density quoted by Cao et al. (2021), such grammage exceeds the total that CRs are expected to accumulate in the Galaxy while diffusing out. One could argue that this conclusion may differ by changing the model of CR injection. Hence, below we consider three models for the origin of the gamma ray emission in an SC. In the first model, CRs are all accelerated in the center of the SC and diffuse outward while interacting with dense clouds (this is the reference model considered by Cao et al. (2021) for the Cygnus region). In the second model, particle acceleration occurs at the termination shock, and particles advect and diffuse outward (Morlino et al. 2021). In the third model, CRs are assumed to be injected in an impulsive event in the center and diffuse outward. The event might be a supernova explosion in the core of the cluster.
We show that in all models listed above, the local grammage traversed by CRs with E ≳ 10 TeV while escaping the SC exceeds the one inferred from secondary/primary ratios (Evoli et al. 2019, 2020; Schroer et al. 2021). The implications for lower energy CRs are also discussed. In light of this finding, we are forced to conclude that either SCs only contribute a negligible fraction of the CRs observed at the Earth or CRs originate in SCs and also accumulate their grammage there rather than in the interstellar medium (ISM) on Galactic scales. This second scenario would require a major revision of the foundations of the model of CR transport in the Galaxy. Alternatively, the gamma ray emission that we measure might be due to leptonic processes, which makes the predictions independent of the gas density. These models (see, e.g., Härer et al. (2023) for such a model applied to Westerlund 1) require a lower strength of the magnetic field in the bubble, which in turn implies that SCs cannot reasonably play the role of PeVatrons. Finally, it might be that the SCs that have been detected so far in gamma rays are unusual, and thus their characteristics are irrelevant for the bulk of the SCs. Although this cannot be excluded, it would definitely be surprising.
If the constraints to the grammage that are inferred here are meaningful for the bulk of SCs, then one should keep them in mind even when supernova remnants (SNRs) are considered as the main source of CRs, since the majority of such sources are expected to be located in SCs. From the observational point of view, an important clue to the origin of the gamma radiation and the constraints on grammage might come from the detection of gamma rays from very young SCs, for which we can be reasonably sure of the absence of SN events taking place at the present time.
This article is organized as follows: in Sect. 2 we discuss the gamma ray emission in the three models of CR production illustrated above. In Sect. 3, we elaborate on the implications of the gamma ray measurements for CR grammage, comparing the results with standard models of CR transport in the Galaxy. In Sect. 4, we outline our conclusions.
2 Models of gamma ray production in star clusters
As we discuss below, the effect of the grammage is so macroscopic that a sophisticated treatment of proton-proton interactions is not necessary. Moreover, in the analysis below, we focus on gamma ray energies >1 TeV, where scaling relations are sufficiently accurate for our purposes here. We assumed that gamma rays with a given energy Eγ are produced by protons with energy E such that Eγ = ηE, with η ≃ 0.1. The cross section for inelastic pp interactions is considered to be constant with energy, σpp = 32 mb.
Here we consider three models of CR transport in the SC. In Model 1 we assumed, following (Lhaaso Collaboration 2024), that a source in the center of the SC continuously injects CRs with a spectrum Q(E) = A(E/mp)–α, with α > 2. We also follow (Lhaaso Collaboration 2024) in assuming that transport is purely diffusive with the diffusion coefficient D(E). In the energy region of interest here, Eγ ≳ 1 TeV, the diffusion equation can be used in its stationary form so that the CR density of energy E at a distance r from the center is
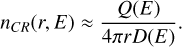 (1)
(1)
We normalized the injection spectrum to a fraction ξCR of the luminosity LSC of the SC (the one that involves plasma motion and can be the seed of particle acceleration) through
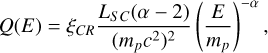 (2)
(2)
where we assumed that the energy in the form of CRs is dominated by relativistic particles, namely E ≳ mp. Within a factor of order unity, this is a good approximation for 2 ≲ α ≲ 3, as expected from diffusive shock acceleration (DSA). These source spectra are also compatible with those found in Lhaaso Collaboration (2024) that provide a good fit to the observed gamma ray emission for the Cygnus region. We note that, quantitatively, including particles with energy lower than mp in the normalization procedure would strengthen the conclusions drawn below.
In the second model (Model 2), we follow Morlino et al. (2021); Blasi & Morlino (2023) in assuming that particle acceleration takes place at the termination shock of the collective wind. The structure of the bubble is properly described by Morlino et al. (2021): the location of the termination shock is at r = Rsh , while the bubble extends to r = Rb . However, as we demonstrate below, these quantities do not need to be written down explicitly. Particle acceleration is assumed to transform a fraction ξCR of the luminosity of the wind, 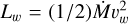 , into CRs. Here, Ṁ is the rate of mass loss in the form of a collective wind, and vw is the wind velocity. The structure of the bubble is such that the shocked wind (i.e., the plasma behind the termination shock) has a velocity v(r) = (vw/4)(r/Rsh)-2, assuming that the termination shock is strong (compression factor of four). The density downstream of the shock is constant. In the wind region (upstream of the termination shock), the velocity is constant to the value vw , while the density is
, into CRs. Here, Ṁ is the rate of mass loss in the form of a collective wind, and vw is the wind velocity. The structure of the bubble is such that the shocked wind (i.e., the plasma behind the termination shock) has a velocity v(r) = (vw/4)(r/Rsh)-2, assuming that the termination shock is strong (compression factor of four). The density downstream of the shock is constant. In the wind region (upstream of the termination shock), the velocity is constant to the value vw , while the density is
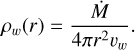 (3)
(3)
Assuming again that the density of accelerated particles at the termination shock has the shape of a power law, nCR(E) = A(E/mp)–α, and that the energy in the form of accelerated particles carries a fraction ξCR of Lw, it is easy to derive
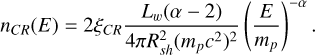 (4)
(4)
In the following, we assume that this density remains constant downstream of the termination shock. While this is a better approximation at E ≲ 1 TeV than at higher energies (where escape from the bubble becomes dominated by diffusion rather than advection), it also maximizes the gamma ray emission, making the results illustrated below even stronger.
In the third model (Model 3), the particles are assumed to be produced in the core of the SC, as in Model 1, but the source is impulsive. This situation might mimic the case of an SN explosion. It is not clear how likely it is to have had an SN explosion in Cygnus or Westerlund 1, although there is evidence for a pulsar in the core in the Cygnus region, with an estimated age of ~105 yr. Since there is no evidence of a shell in the bubble, we assumed that the SN event occurred ≲105 years ago. Once produced, CRs are assumed to diffuse outward and eventually escape.
If ESN is the kinetic energy of the SN ejecta, then the density of particles in the bubble can be estimated as
![${n_{CR}}(E) \approx {{{\xi _{CR}}{E_{SN}}(\alpha - 2)} \over {{{\left( {{m_p}{c^2}} \right)}^2}{{[4\pi D(E)t]}^{3/2}}}}{\left( {{E \over {{m_p}}}} \right)^{ - \alpha }},{\rm{r}} < \sqrt {4Dt} .$](/articles/aa/full_html/2025/02/aa53017-24/aa53017-24-eq6.png) (5)
(5)
We note that the condition that particles of energy E are still inside the SC at time t imposes an upper limit on the diffusion coefficient D(E):
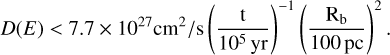 (6)
(6)
We also note that the particles at time t uniformly fill a sphere of radius 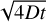 , while their density drops∝ exp[–r2/4Dt] at larger distances. For simplicity, we assumed that the particles are all concentrated with the diffusion distance.
, while their density drops∝ exp[–r2/4Dt] at larger distances. For simplicity, we assumed that the particles are all concentrated with the diffusion distance.
2.1 Gamma ray emission in Model 1: Diffusion model
In the following, we denote as ngas the mean gas density in the bubble, which is to be interpreted as the volume averaged gas density, dominated by the clumpy structure of atomic and molecular gas (see discussion in Blasi & Morlino 2024). We assumed that this density is constant throughout the bubble since the available information on the spatial distribution of the gas is very poor (also see the discussion in Menchiari 2023).
As discussed above, in Model 1 (Lhaaso Collaboration 2024), we assume that a source in the SC core injects CRs at a constant rate and that these particles move outward only due to diffusion. In this simple picture there is no bulk motion of the plasma, so it mimics a situation where the SC is unable to launch a collective wind (although even in that case it is difficult to imagine that a collective motion may be completely absent). As argued by Vieu et al. (2024), this might be the case of the Cygnus cocoon.
The emissivity in the form of gamma rays can be written as
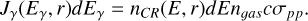 (7)
(7)
Using the assumption that Eγ = ηE, one can write
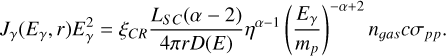 (8)
(8)
It follows that the gamma ray flux from the entire bubble can be estimated as
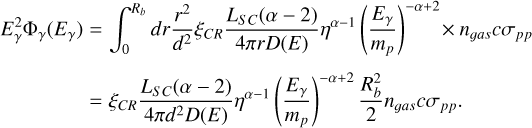 (9)
(9)
The escape time from the bubble in a purely diffusive case is 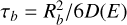 , so we can introduce the grammage traversed by particles while escaping the bubble as
, so we can introduce the grammage traversed by particles while escaping the bubble as
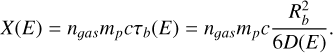 (10)
(10)
This allows us to rewrite Eq. (9) as
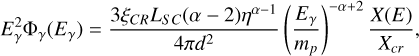 (11)
(11)
where Xcr = mp/σpp is the critical grammage for pp interactions. As written here, this expression can also be used, within factors of order unity, when the gas is not uniformly distributed, for instance when the whole gas is concentrated in a thin shell at the edge of the bubble.
2.2 Gamma ray emission in Model 2: Acceleration at the termination shock
With the same assumptions on pp collisions adopted above, the gamma ray emissivity in the case of particle acceleration at the termination shock can be written as
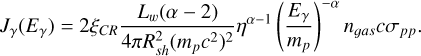 (12)
(12)
The integral over the downstream of the termination shock, the region that dominates the gamma ray emission in this model, leads to
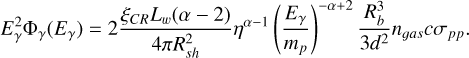 (13)
(13)
To maximize the gamma ray flux predicted by the model and make our conclusions more solid, we assumed that particle escape from the bubble is dominated by advection. As discussed by Blasi & Morlino (2024), escape becomes dominated by diffusion at energies ≳1 TeV, but this leads to a smaller effective emission region for gamma rays and correspondingly smaller gamma rays ray flux; hence, our assumption is conservative in terms of deriving constraints on the grammage inside the bubble. Recalling that the plasma velocity drops downstream of the termination shock, we can write
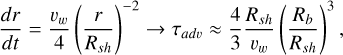 (14)
(14)
where for simplicity we assumed that Rb >> Rsh. Replacing this expression in Eq. (13), we easily obtain
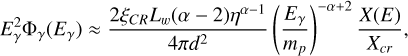 (15)
(15)
where the grammage is defined as X(E) = ngasmpcτadv. A quick comparison between Eqs. (11) and (15) immediately suggests that Models 1 and 2 are going to lead to very similar constraints in terms of grammage.
 |
Fig. 1 Lower limits to the grammage inferred for the Cygnus region (left) and Westerlund 1 (right) if the observed gamma rays are of hadronic origin in three models of gamma ray production as described in the text. These limits are shown together with an up-to-date computation of the Galactic CR grammage inferred from secondary/primary ratios (Schroer et al. 2021). The yellow shadowed region shows the maximum source grammage still compatible with secondary to primary ratios (≃0.4 g cm–2). |
2.3 Gamma ray emission in Model 3: Impulsive injection of cosmic rays
The detection of gamma rays of energy Eγ implies that the parent CR particles, with energy E = Eγ/η, are still confined inside the SC. This trivially implies that the gamma ray spectrum integrated over the volume is insensitive to the diffusion coefficient. Hence the flux of gamma rays can be written using Eq. (5) integrating on 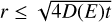 :
:
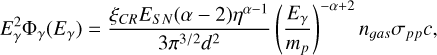 (16)
(16)
with the usual meaning of the symbols. It is worth noting how this result, contrary to the ones obtained for the other two models, depends only on the density of the target gas and not on the grammage. On the other hand, as discussed above (see Eq. (6)), the condition that particles are still trapped in the bubble after a time t allows us to infer a lower limit to the grammage traversed by particles before they are released into the ISM.
3 Constraints on the grammage inside the Cygnus cocoon and Westerlund 1
The LHAASO experiment has recently measured the gamma ray flux with energy above ~1 TeV from the Cygnus cocoon at the level of 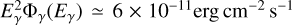 over a region that extends ~150 pc from the center of Cygnus SC. The emission is claimed to have a hadronic origin, and it is difficult to imagine otherwise given the extended morphology. The slope of the spectrum is ~2.7 (at E ≳ 1 TeV) and probably reflects the energy-dependent diffusion coefficient, together with the shape of the spectrum near the maximum energy. This point, however, is of little interest here in that we focus on the lowest energy bin, at 1 TeV, and investigate the dependence of our constraints on the value of α, the slope of the injection spectrum. The HESS telescope has observed gamma rays from the direction of the SC Westerlund 1 (Aharonian et al. 2022), with
over a region that extends ~150 pc from the center of Cygnus SC. The emission is claimed to have a hadronic origin, and it is difficult to imagine otherwise given the extended morphology. The slope of the spectrum is ~2.7 (at E ≳ 1 TeV) and probably reflects the energy-dependent diffusion coefficient, together with the shape of the spectrum near the maximum energy. This point, however, is of little interest here in that we focus on the lowest energy bin, at 1 TeV, and investigate the dependence of our constraints on the value of α, the slope of the injection spectrum. The HESS telescope has observed gamma rays from the direction of the SC Westerlund 1 (Aharonian et al. 2022), with 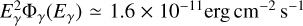 at Eγ = 1 TeV. In the following, we adopt a distance of 1.4 kpc for Cygnus and 3.9 kpc for Westerlund 1.
at Eγ = 1 TeV. In the following, we adopt a distance of 1.4 kpc for Cygnus and 3.9 kpc for Westerlund 1.
In Model 1, we normalized the luminosity to LSC = 1039L39 erg/s. We note that photons with energy Eγ are produced by protons with energy E = 10 TeV; hence, we are able to constrain the grammage traversed in the SC by protons with 10 TeV energy. The gamma ray flux computed using Eq. (11) can be written as 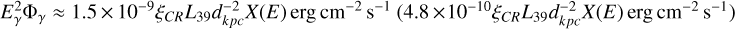 for α = 2.2 (α = 2.4). Comparing this prediction with the flux as measured by LHAASO for the Cygnus cocoon, we obtain a grammage
for α = 2.2 (α = 2.4). Comparing this prediction with the flux as measured by LHAASO for the Cygnus cocoon, we obtain a grammage 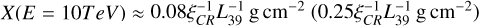
Finally, when requiring a reasonable efficiency of particle acceleration, say ξCR ≲ 0.1, we immediately inferred that in order to account for the gamma ray flux observed by LHAASO, the grammage required for Model 1 has to be 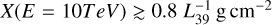 for α = 2.2 and
for α = 2.2 and 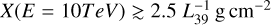 for α = 2.4. A similar procedure leads to a lower limit to the grammage in the case of Westerlund 1. Both sets of limits are plotted in Fig. 1 for Cygnus (left panel) and Westerlund 1 (right panel). The figure also shows the grammage traversed by CRs during their journey through the Galaxy, as inferred from sec- ondary/primary ratios (see for instance Evoli et al. 2019, 2020; Schroer et al. 2021). The yellow shaded region shows the largest grammage (the so-called source grammage) that would still be compatible with the measured ratios. Interestingly, this grammage is not too far from the one expected to be accumulated while CRs are downstream of the shock of a SNR (Aloisio et al. 2015). Any grammage in excess of ~0.4g cm–2 would force us to revisit the very foundations of the picture of CR transport in the Galaxy.
for α = 2.4. A similar procedure leads to a lower limit to the grammage in the case of Westerlund 1. Both sets of limits are plotted in Fig. 1 for Cygnus (left panel) and Westerlund 1 (right panel). The figure also shows the grammage traversed by CRs during their journey through the Galaxy, as inferred from sec- ondary/primary ratios (see for instance Evoli et al. 2019, 2020; Schroer et al. 2021). The yellow shaded region shows the largest grammage (the so-called source grammage) that would still be compatible with the measured ratios. Interestingly, this grammage is not too far from the one expected to be accumulated while CRs are downstream of the shock of a SNR (Aloisio et al. 2015). Any grammage in excess of ~0.4g cm–2 would force us to revisit the very foundations of the picture of CR transport in the Galaxy.
In fact, this seems to be the case for both Cygnus and Wester- lund 1 if the gamma ray emission is of hadronic origin. Model 1 leads us to expect a grammage in both cases appreciably larger than the Galactic grammage at 10 TeV. Even more concerning, in Model 1, this grammage would extend to lower energies as a power law, so the conclusions above would also apply to lower energies, where the grammage is even better constrained.
Finally, we note that the limit above has been specialized to an SC luminosity of 1039 erg/s, which is probably somewhat larger than the actual luminosity of the two SCs considered here. For lower values of the luminosity, the limits would become correspondingly stronger.
In Model 2, we normalized the wind luminosity to Lw = 1039Lw,39 erg/s. The gamma ray flux computed using Eq. (15) can be written as 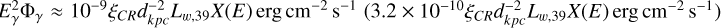 for α = 2.2 (α = 2.4). Following the same procedure outlined for Model 1 and requiring efficiency ξCR < 0.1, we inferred the corresponding lower limits on the grammage, as shown in Fig. 1 (green symbols for Model 2). The problem discussed above with the grammage appears to be even more severe for Model 2.
for α = 2.2 (α = 2.4). Following the same procedure outlined for Model 1 and requiring efficiency ξCR < 0.1, we inferred the corresponding lower limits on the grammage, as shown in Fig. 1 (green symbols for Model 2). The problem discussed above with the grammage appears to be even more severe for Model 2.
We note that the limits derived for Model 2 should be considered as absolute lower limits to the grammage since we neglected the diffusive escape of CRs from the cocoon at E ≳ 1 TeV (Blasi & Morlino 2024), which would reduce the high energy CR density and increase the required grammage. These limits are in line with the results presented by Blasi & Morlino (2023, 2024), where a gas density ngas ~ 5–10 cm–3 was used, which is in line with the values inferred by the Lhaaso Collaboration (2024). Using the expressions above, this would correspond to a CR acceleration efficiency at the termination shock ξCR ~ 0.5%, in agreement with the values found by Blasi & Morlino (2023). This, however, implies a grammage in the cocoon of ~50 g cm-2 and is thus well in excess of the Galactic grammage. Not surprisingly, such a grammage was found to be responsible for the complete spallation of heavy nuclei and a slight difference between the escaping spectra of H and He nuclei (Blasi & Morlino 2024). SCs with characteristics similar to those of the Cygnus cocoon and Westerlund 1 cannot account for the bulk of Galactic CRs unless CR transport is deeply revised. Alternatively, the gamma ray emission may not be due to hadronic interactions, as suggested by Härer et al. (2023) for Westerlund 1.
In Model 3, we tested the possibility that CRs have been injected in the bubble during an impulsive event at a time t in the past and that the gamma ray emission is being produced by such particles today. The condition that CRs of energy E are still confined inside the bubble leads to an upper limit to the diffusion coefficient, 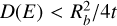 . Comparing between Eq. (16) and the observed gamma ray flux from an SC allowed us to impose a lower limit to the gas density in the bubble by requiring ξCR ≤ 0.1. For Cygnus, this limit reads ngas > Nmin = 62 cm–3 for α = 2.2 and ngas > nmin = 131 cm–3 for α = 2.4. The combination of these two conditions implies that the grammage must satisfy
. Comparing between Eq. (16) and the observed gamma ray flux from an SC allowed us to impose a lower limit to the gas density in the bubble by requiring ξCR ≤ 0.1. For Cygnus, this limit reads ngas > Nmin = 62 cm–3 for α = 2.2 and ngas > nmin = 131 cm–3 for α = 2.4. The combination of these two conditions implies that the grammage must satisfy
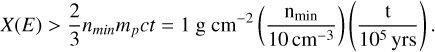 (17)
(17)
One can see that not only the values of density in this model appear extreme and hard to reconcile with the formation of a bubble, but also the inferred grammage exceeds the Galactic grammage, more so than in Models 1 and 2 discussed above. In Fig. 1, we only show the limit on the grammage for Model 3 for the cases in which the limit is lower than 10 g cm-2. Similar considerations apply to the case of Westerlund 1.
4 Discussion
Star clusters have long been thought to play an important role in the framework of the origin of Galactic CRs in at least two ways: first, by providing enough CRs to justify the excess of 22Ne observed in the cosmic radiation and, second, by possibly providing the right conditions for acceleration up to the knee, something that SNRs seem to struggle to do. The recent detection of selected SCs in high energy gamma rays has fueled renewed interest in this problem, especially in the perspective of SCs playing the role of PeVatrons. As discussed by Morlino et al. (2021); Blasi & Morlino (2023), it seems unlikely that SCs would efficiently accelerate particles up to the knee energy at the termination shock generated by the collective wind. It cannot yet be excluded that higher energies may be reached in SN explosions occurring inside an SC. This latter scenario would apply to SCs that are old enough to host SN explosions.
Here, we have discussed the implications of the recently observed gamma ray emission from selected SCs in terms of their contribution to the bulk of Galactic CRs. In particular, we have shown that the gamma ray emission observed by LHAASO from the direction of the Cygnus cocoon (Cao et al. 2021; Lhaaso Collaboration 2024) and by HESS from the direction of West- erlund 1 (Aharonian et al. 2022) lead to an estimate of the grammage accumulated by particles while leaving the bubble region that exceeds the Galactic grammage at ~10 TeV. The way this finding extends to lower energies depends on the model adopted to describe the gamma ray emission. Even if this grammage were energy independent, the accumulated grammage at low energies would require substantial revision of the transport of Galactic CRs in order to accommodate the excess grammage.
If one takes for granted the average gas density in the Cygnus cocoon, ngas = 5–10 cm–3, as inferred in much of the recent literature (Aharonian et al. 2019; Cao et al. 2021; Menchiari 2023; Menchiari et al. 2024a), the inferred grammage would be X ~ 25–50 g cm–2, which is larger than the total grammage traversed by CRs at ~ 10 GeV by about one order of magnitude. Not surprisingly, the calculations of Blasi & Morlino (2024), applied to the Cygnus cocoon, imply that nuclei heavier than He are basically destroyed inside the cocoon, and even for He the spallation reactions are sufficiently severe to harden the He spectrum with respect to H nuclei.
It is clear that the discovery of high energy gamma ray emission from SCs and most notably from Cygnus and Westerlund 1 represents a milestone in our field of investigation, and it provides a possible clue to the origin of high energy CRs. But the same detection also implies that either SCs cannot contribute but a small fraction of Galactic CRs or our understanding of how CRs accumulate grammage in the Galaxy needs to be deeply revised. Clearly these conclusions are based on assumptions that may be flawed. For instance, one could speculate that the SCs detected in gamma rays are not representative of the whole class of SCs, implying that perhaps most SCs are not bright in gamma rays. The other possibility is that the gamma radiation observed so far is of leptonic origin, so it becomes uncorrelated with the grammage traversed in the source.
We note that if most SCs are hadronic gamma ray emitters, as discussed by Menchiari et al. (2024b), they would contribute significantly to the diffuse Galactic gamma ray background. On the other hand, while there is substantial correlation between unidentified Fermi-LAT sources and young SCs, no such strong correlation arises in the TeV range or with SCs that are older than a few million years (Peron et al. 2024b), suggesting that Cygnus and Westerlund might be exceptional. Clearly both of these issues require more attention to assess the role of SCs as potential CR sources.
Models of the origin of Galactic CRs in which grammage is accumulated near sources were actually developed by Cowsik & Wilson (1975) and recently revised by Cowsik & Huth (2022) as a possible way to address the issue of a rising positron fraction. In general, these models struggle to accommodate the features observed in the spectra of primary nuclei and the decay of 10Be. Nevertheless, it is worth keeping in mind the possibility that at least part of the grammage inferred from measurements at the Earth may be accumulated in or around the sources rather than en route to the Earth.
Acknowledgements
This work has been partially funded by the European Union – Next Generation EU, through PRIN-MUR 2022TJW4EJ and by the European Union – NextGenerationEU under the MUR National Innovation Ecosystem grant ECS00000041 – VITALITY/ASTRA – CUP D13C21000430001. The author is grateful to E. Amato, C. Evoli, S. Menchiari, G. Morlino, G. Peron and E. Sobacchi for useful conversations and to B. Schroer for providing the grammage from Schroer et al. (2021).
References
- Abeysekara, A. U., Albert, A., Alfaro, R., et al. 2021, Nat. Astron., 5, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, A&A, 537, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2011, Science, 334, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2011, Science, 332, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Akaike, Y., Asano, K., et al. 2022, Phys. Rev. Lett., 129, 101102 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Akaike, Y., Asano, K., et al. 2023, Phys. Rev. Lett., 130, 171002 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Aisa, D., Alpat, B., et al. 2015a, Phys. Rev. Lett., 115, 211101 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Aisa, D., Alpat, B., et al. 2015b, Phys. Rev. Lett., 114, 171103 [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Yang, R., & de Oña Wilhelmi, E. 2019, Nat. Astron., 3, 561 [Google Scholar]
- Aharonian, F., Ashkar, H., Backes, M., et al. 2022, A&A, 666, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ahn, H. S., Allison, P., Bagliesi, M. G., et al. 2010, ApJ, 714, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, A., Alfaro, R., Alvarez, C., et al. 2021, ApJ, 907, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Alemanno, F., An, Q., Azzarello, P., et al. 2021, Phys. Rev. Lett., 126, 201102 [NASA ADS] [CrossRef] [Google Scholar]
- Aloisio, R., Blasi, P., & Serpico, P. D. 2015, A&A, 583, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- An, Q., Asfandiyarov, R., Azzarello, P., et al. 2019, Sci. Adv., 5, eaax3793 [CrossRef] [Google Scholar]
- Blasi, P., & Morlino, G. 2023, MNRAS, 523, 4015 [CrossRef] [Google Scholar]
- Blasi, P., & Morlino, G. 2024, MNRAS, 533, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, Z., Aharonian, F. A., An, Q., et al. 2021, Nature, 594, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Cowsik, R., & Huth, D. 2022, Adv. Space Res., 70, 2714 [NASA ADS] [CrossRef] [Google Scholar]
- Cowsik, R., & Wilson, L. W. 1975, in International Cosmic Ray Conference, 2, International Cosmic Ray Conference, 659 [NASA ADS] [Google Scholar]
- Evoli, C., Aloisio, R., & Blasi, P. 2019, Phys. Rev. D, 99, 103023 [CrossRef] [Google Scholar]
- Evoli, C., Morlino, G., Blasi, P., & Aloisio, R. 2020, Phys. Rev. D, 101, 023013 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, S., Nath, B. B., Sharma, P., & Eichler, D. 2020, MNRAS, 493, 3159 [CrossRef] [Google Scholar]
- Härer, L. K., Reville, B., Hinton, J., Mohrmann, L., & Vieu, T. 2023, A&A, 671, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H. E. S. S. Collaboration (Abramowski, A., et al.) 2015, Science, 347, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Lhaaso Collaboration 2024, Sci. Bull., 69, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Menchiari, S. 2023, Ph.D. Thesis [arXiv:2307.03477] [Google Scholar]
- Menchiari, S., Morlino, G., Amato, E., Bucciantini, N., & Beltrán, M. T. 2024a, A&A, 686, A242 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menchiari, S., Morlino, G., Amato, E., et al. 2024b, A&A, submitted [arXiv:2406.04087] [Google Scholar]
- Morlino, G., Blasi, P., Peretti, E., & Cristofari, P. 2021, MNRAS, 504, 6096 [NASA ADS] [CrossRef] [Google Scholar]
- Peron, G., Casanova, S., Gabici, S., Baghmanyan, V., & Aharonian, F. 2024a, Nat. Astron., 8, 530 [CrossRef] [Google Scholar]
- Peron, G., Morlino, G., Gabici, S., et al. 2024b, ApJ, 972, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, L., Domínguez, A., Tibaldo, L., et al. 2020, ApJ, 897, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Schroer, B., Evoli, C., & Blasi, P. 2021, Phys. Rev. D, 103, 123010 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X.-N., Yang, R.-Z., Liang, Y.-F., et al. 2020, A&A, 639, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieu, T., Gabici, S., Tatischeff, V., & Ravikularaman, S. 2022, MNRAS, 512, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Vieu, T., Larkin, C. J. K., Härer, L., et al. 2024, MNRAS, 532, 2174 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. 2024, arXiv e-prints [arXiv:2406.03555] [Google Scholar]
- Yang, R.-z., de Oña Wilhelmi, E., & Aharonian, F. 2018, A&A, 611, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Lower limits to the grammage inferred for the Cygnus region (left) and Westerlund 1 (right) if the observed gamma rays are of hadronic origin in three models of gamma ray production as described in the text. These limits are shown together with an up-to-date computation of the Galactic CR grammage inferred from secondary/primary ratios (Schroer et al. 2021). The yellow shadowed region shows the maximum source grammage still compatible with secondary to primary ratios (≃0.4 g cm–2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


