| Issue |
A&A
Volume 692, December 2024
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 22 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202349005 | |
| Published online | 29 November 2024 | |
Origin of the spectral features observed in the cosmic-ray spectrum
1
INAF-Osservatorio Astronomico di Brera, Via Bianchi 46, I-23807 Merate, Italy
2
Dipartimento di Fisica, Università di Torino, via P. Giuria 1, 10125 Torino, Italy
3
Istituto Nazionale di Fisica Nucleare, Sezione di Torino, Via P. Giuria 1, 10125 Torino, Italy
4
Université Paris Cité, CNRS, Astroparticule et Cosmologie, F-75013 Paris, France
⋆ Corresponding author; sarah.recchia@inaf.it
Received:
18
December
2023
Accepted:
10
October
2024
Context. Recent measurements reveal the presence of several features in the cosmic-ray (CR) spectrum. In particular, the proton and helium spectra exhibit a spectral hardening at ≈300 GV and a spectral steepening at ≈15 TV, followed by the well-known knee-like feature at ≈3 PV. The spectra of heavier nuclei also harden at ≈300 GV, while no claim can be currently made about the presence of the ≈15 TV softening, due to low statistics. In addition, the B/C ratio also exhibits a hardening at ≈100 GeV/n and seems to be rather shallow at ≈1 TeV/n
Aims. We propose a possible explanation of the observed spectral features in the framework of a composite diffusion scenario and considering different classes of sources.
Methods. The proposed scenario is based on two assumptions. First, in the Galactic disk, where magnetic field lines are mainly oriented along the Galactic plane, particle scattering is assumed to be very inefficient. Therefore, the transport of CRs from the disk to the halo is set by the magnetic field line random walk induced by large-scale turbulence. Second, we propose that the spectral steepening at ≈15 TV is related to the typical maximum rigidity reached in the acceleration of CRs by the majority of supernova remnants, while we assume that only a fraction of sources, contributing to ≈10 − 20% of the CR population, can accelerate particles up to ∼PV rigidities.
Results. Within this framework we show that it is possible to reproduce the proton and helium spectra from GV to multi-PV; the p/He ratio; the spectra of CRs from lithium to iron; the p̄ flux and the p̄/p ratio; and the abundance ratios B/C, B/O, C/O, Be/C, Be/O, and Be/B. We also discuss the 10Be/9Be ratio in view of the recent AMS02 preliminary measurements.
Key words: diffusion / cosmic rays / Galaxy: disk / Galaxy: halo
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The standard paradigm of the origin of cosmic rays (CRs) is based on three main pillars. First, the bulk of primary CRs is accelerated out of the interstellar medium (ISM), presumably up to the energy of the knee (E ≈ 3 PeV) and beyond, at the shocks of supernova remnants (SNRs). The acceleration mechanism, diffusive shock acceleration (DSA), is rigidity-dependent (R) and produces power-law CR spectra ∝R−α (α ≈ 2.0 − 2.4). Second, CRs are diffusively confined in a magnetized Galactic halo (GH) a few kiloparsecs in height (H). The CR residence time in such a halo decreases with rigidity as τres(R) = H2/D(R)∝R−δ (δ ≈ 0.3 − 0.6). The equilibrium spectrum is then ∝R−α − δ with α + δ ∼ 2.7, which roughly describes the CR observed primary spectra. Third, secondary CRs (such as Li, Be, B, p̄) are produced in CR interactions with matter during the repeated crossings of the Galactic disk (GD, height h ∼ 150 pc, density nd ∼ 1 cm−3) that CRs perform before leaving the Galaxy. The relative abundance of secondary to primary elements at high enough R are expected to be proportional to the grammage (average amount of matter) traversed by CRs during the Galactic propagation,  , where
, where  is the average ISM density in the propagation volume, μ ∼ 1.4 mp is the mean mass of ISM nuclei, and v ∼ c is the CR particle velocity. We also note that
is the average ISM density in the propagation volume, μ ∼ 1.4 mp is the mean mass of ISM nuclei, and v ∼ c is the CR particle velocity. We also note that  corresponds to the residence time in the disk, which can then be derived directly from the measured grammage X = ndμvτd. The total residence time in the Galaxy, τres, can be determined by the measure of the grammage combined with that of the short-lived radioisotope 10Be, which can be used as a CR clock (Ptuskin & Soutoul 1998). By doing so, one obtains
corresponds to the residence time in the disk, which can then be derived directly from the measured grammage X = ndμvτd. The total residence time in the Galaxy, τres, can be determined by the measure of the grammage combined with that of the short-lived radioisotope 10Be, which can be used as a CR clock (Ptuskin & Soutoul 1998). By doing so, one obtains  , with
, with  and δ ≈ 0.3 − 0.6 (Blasi 2013; Gabici et al. 2019).
and δ ≈ 0.3 − 0.6 (Blasi 2013; Gabici et al. 2019).
In recent times, an impressive amount of high-precision CR data and refined theoretical models and simulations have become available. This has challenged the standard picture in several ways (see, e.g., Gabici et al. 2019, for a critical review of the SNR paradigm). Some of the main issues that emerged are briefly illustrated in the remainder of this section.
The Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics (PAMELA; Adriani et al. 2011) and the Alpha Magnetic Spectrometer (AMS02; Aguilar et al. 2015) experiments reported on a spectral hardening at R ∼ 300 GV in the proton and helium spectra. This feature is explained by a change in the rigidity dependence of the diffusion coefficient (Tomassetti 2012; Aloisio & Blasi 2013; Tomassetti 2015; Génolini et al. 2017; Di Mauro et al. 2024), due, for instance, to a change from scattering on self-generated turbulence to preexisting turbulence. This hypothesis has recently been confirmed by the measurement of a hardening in the spectra of secondary CRs (e.g., Li, Be, B), which is two times more pronounced than that observed in the proton and helium spectra (Aguilar et al. 2018, 2021d). Alternative explanations invoking the presence of a nearby source (Thoudam & Hörandel 2012) or nonlinear effects in particle acceleration (Ptuskin et al. 2013; Recchia & Gabici 2018) now seem to be disfavored.
More recent data (Adriani et al. 2020; Dampe Collaboration 2022) confirmed the presence of the hardening in the B/C ratio previously found by Aguilar et al. (2018) and Aguilar et al. (2021d) at ≈100 GeV/n, and measured this ratio up to a few TeV/n. Interestingly, the energy dependence of B/C becomes progressively shallower above the break, with an estimated slope of γB/C ≈ 0.2 for the Dark Matter Particle Explorer (DAMPE) data and γB/C ≈ 0.28 for the Calorimetric Electron Telescope (CALET) data. Moreover, the NUCLEON data (Grebenyuk et al. 2019b) suggest a rather flat B/C around a total energy per nucleon of ≈1 TeV/n, although with large error bars.
The measured value is B/C (TeV/n) ≈ 0.04 (see Fig. 1), which can be converted into a grammage equal to (Evoli et al. 2019)
 |
Fig. 1. B/C (top panel), B/O (middle panel), and C/O (bottom panel) ratios compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2020, blue squares), and DAMPE (Dampe Collaboration 2022, cyan triangles). The solid red (dashed magenta) line corresponds to the ratio as a function of rigidity (kinetic energy per nucleon) and is compared to the AMS02 (CALET and DAMPE) data. The green (pink) shaded region corresponds to a 20% uncertainty in the secondary production cross section. The solid blue line corresponds to the B/C or B/O ratio when the B flux is multiplied by fB = 1.1, as in Fig. 7. |
which in turn corresponds to a residence time in the disk of
In addition, the p̄/p ratio appears rather flat above ≈30 GV (Aguilar et al. 2016, see also Fig. 2) and a similar behavior is found in the e+/p ratio. The latter is related to the issue of the rising positron fraction (Aguilar et al. 2013); however, this is typically explained with the contribution to positrons from middle-aged pulsars (see, e.g., Hooper et al. 2009). The former has been discussed in the literature in connection to possible contributions to the antiproton flux other than secondary production in the Galaxy, and in particular to possible dark matter signals. At the same time, much effort has been devoted to assess the expected secondary flux with the most up-to-date production cross sections; some works find the latter to be consistent with the observed flux (see, e.g., Boudaud et al. 2020). The rather shallow scaling with energy of these abundance ratios posed the question on whether the grammage is uniquely accumulated during the large-scale propagation of CRs in the Galaxy or if it may include a relevant contribution accumulated inside or in the vicinity of CR sources.
 |
Fig. 2. Antiprotons. Top left panel: Unmodulated (solid orange) and modulated (dashed red) p̄ flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots). The yellow (green) shaded region corresponds to a 10% (20%) uncertainty in the production cross section. Top right panel: p̄/p ratio compared to the data of AMS02 (Aguilar et al. 2021d, black dots). Bottom left panel: p̄ source term, computed as in Eq. (23) and corresponding to the flux reported in the top left panel of the present figure. Bottom right panel: Slopes of the p̄ source term (solid green line), of p̄ flux (blue solid line), and of the proton flux (red solid line) reported in Fig. 4. The solid cyan curve corresponds to the sum of the slope of |
Having in mind SNRs as the main accelerators of CRs, the source or near-source contribution to the grammage may come from three sources: i) secondaries produced at the shock that either leave rapidly the acceleration site or get re-accelerated before escaping. In the former case the secondary spectrum is similar to the primary spectrum, while in the latter case the secondary spectrum is harder (see, e.g., Tomassetti & Donato 2012; Bresci et al. 2019; Mertsch et al. 2021 and references therein); ii) seed secondary CRs (produced by spallation in the ISM) that are re-accelerated by shocks, a process that produces secondary spectra similar to primaries (Tomassetti & Donato 2012; Bresci et al. 2019); and (iii) the production of secondaries by CRs that are confined in the vicinity of SNRs. In this case, the spectra of secondaries are typically steeper than those of primaries, depending on the rigidity-dependent residence time, for example due to self-confinement processes (D’Angelo et al. 2016; Recchia et al. 2022).
The first two effects are unavoidable and are potentially significant above R ≈ 1 TV, as shown in recent works (Bresci et al. 2019; Mertsch et al. 2021), but their actual relevance is a matter of debate. Their impact on secondary production ultimately depends on the very poorly understood time evolution of the maximum rigidity Rmax(t) at SNR shocks, on the duration of effective acceleration up to and above the TV, on the density of the medium in which SNRs explode (for the first process) and on the volume spanned by SNRs during efficient acceleration up to TeV energies (relevant for re-acceleration) (Tomassetti & Donato 2012). For the third process, its relevance depends on the effectiveness of confinement in the source region, on the density of the background, on its level of ionization and turbulence, and on the energy dependence of the residence time (see, e.g., the discussion by Recchia et al. 2022 and references therein).
In this context Cowsik & Burch (2010) proposed a radically different point of view (see also Cowsik & Madziwa-Nussinov 2016), where CRs up to ∼1 TV are confined for long and R-dependent times in dense cocoons around accelerators, and escape from the Galaxy in a R-independent way. The residence time in the Galaxy is assumed to be rather small, so that positrons would not suffer much from energy losses, a hypothesis also discussed in detail by Lipari (2017). In this scenario the authors try to explain the flat p̄/p and e+/p. This class of models is surely very interesting, but the formation of cocoons and the possibility of long confinement times in these regions remains an open issue, and may be plagued by the same difficulties of models of CR self-confinement around sources (Recchia et al. 2022). Moreover it requires a number of conditions that need to be justified theoretically, such as a steep injection spectrum of protons, little energy loss for leptons, and at the same time different source spectra for nuclei and leptons.
While there is a wide consensus on the fact that SNRs may accelerate the bulk of CRs, the maximum R that can be reached in the acceleration process is a matter of intense debate. The most popular hypothesis is that the spectral steepening at a few PeV (the knee) is the result of SNRs accelerating light nuclei (proton and helium) up to such energy, and heavier nuclei up to energies Z (ion charge) times larger. The detection of gamma rays from SNRs of GeV to multi-TeV confirmed that efficient particle acceleration is indeed taking place there, but so far there has been no clear evidence of PeV acceleration (see, e.g., Gabici et al. 2016; Cristofari 2021).
Theoretical models show that particle acceleration to PeV energies requires a substantial amplification of the magnetic field at the shock. Remarkably, X-ray measurements at SNR shocks detected values of B that are much larger than the typical μG scale of the ISM, even at the level of hundreds of μG (see, e.g., Vink 2012). However, current theories show that in SNRs a PeVatron phase may be present only in the ejecta-dominated phase and in a subclass of peculiar objects that explode in a dense environment and have large shock speeds, and that this phase may last for short times, on the order of ≈100s yr (Bell et al. 2013; Cristofari et al. 2020; Cristofari 2021). Alternative scenarios propose powerful stellar winds and supernovae in compact clusters of massive stars and OB associations (see, e.g., Bykov et al. 2020 for a review) as potential PeVatrons and as a possible explanation for the 22Ne/20Ne anomalous isotopic ratio, with a overall contribution to the CR population of ≈5 − 10% (Tatischeff et al. 2021; Vieu & Reville 2023).
It is also possible that only a subset of SNRs accelerate particles up to PeV energies and beyond. In this case, a crucial issue would be to determine the maximum energy reached in typical SNRs, the overall CR luminosity of such typical sources and PeV sources, and the possible spectral features emerging from the presence of (at least) these two classes of sources (typical SNRs and PeV SNRs). Interestingly, DAMPE (An et al. 2019; Alemanno et al. 2021) recently found an additional spectral steepening in the proton and helium spectra at ≈15 TV between the spectral hardening at ≈300 GV and the knee. As in the case of the ≈300 GV break, possible explanations that have been put forward involve a nearby source (Fornieri et al. 2021b; Malkov & Moskalenko 2022; Luo et al. 2022; Lagutin & Volkov 2024), effects related to the acceleration process (Kamijima & Ohira 2022), or a change in the propagation regime (Chernyshov et al. 2024).
The CR diffusive transport in the GH is thought to be due to the particle scattering on magnetic inhomogeneities whose wavelength is comparable to the particle’s Larmor radius, rL, a process called resonant scattering (Skilling 1975). The rigidity dependence of the diffusion coefficient reflects the spectral properties of the turbulence at the resonant scale (see, e.g., Fornieri et al. 2021a).
For the GD, and in general for the near-disk region, it is not clear whether CRs can be well scattered. In particular, the scattering of ≲TeV particles can be hampered, for example due to a very effective damping of the turbulence by ion-neutral friction (Recchia et al. 2022, see also the discussion on the formation of the diffusive halo by Evoli et al. 2018a). At higher energies very weak scattering may be the result of the possibly anisotropic cascade of the turbulence injected by astrophysical sources (although intermittency may enhance scattering, as recently showed by Lemoine 2023; Kempski et al. 2023), while there are too few CRs to be able to excite enough resonant waves.
In general, the GD is either regarded as an infinitesimally thin (compared to the GH) passive target for secondary production, where CR crossing takes place at the speed of light, or the propagation there is assumed to be diffusive with the same diffusion coefficient of the GH. However, while CR data at R ≲ TeV can be well reproduced with such assumptions, hints that the particle transport in the GD and in the GH may be substantially different emerged in a variety of observations and theoreticalinvestigations.
For instance, the extended γ-ray halos detected around the Geminga and Monogem pulsars (Abeysekara et al. 2017) and likely produced by runaway electrons and positrons of ≈ 20 − 200 TeV, suggest that the CR diffusion coefficient in the disk (or at least in some regions) for such high-energy particles may be ≈100 − 1000 times smaller than that inferred from B/C and extrapolated to high energies. Moreover, Jacobs et al. (2023) recently suggested that an average diffusion coefficient in GD (resulting from the presence of low-diffusion zones with a given filling factor in the disk) a few times smaller than in the GH may help in reproducing the preliminary 10Be/9Be ratio measurements reported by AMS02. This finding may seem in contradiction with a weak particle scattering in the GD. However, as illustrated in Sect. 2, it is possible to reconcile the two by taking the anisotropic CR transport into account.
The particle propagation in a magnetized environment exhibits substantial differences between the particle motion along and across the average magnetic field (Shalchi 2020; Mertsch 2020). If the intensity of the turbulent field is significantly lower than the mean large-scale field, particle diffusion primarily takes place along field lines. The particle propagation perpendicular to the average field is a combination of the random motion of field lines (field line random walk, FLRW), induced by large-scale fluctuations and usually dominant, and of perpendicular (cross-field) diffusion. Interestingly, the large-scale Galactic magnetic field in the GD is mainly parallel to the Galactic plane (GP), while in the GH is preferentially perpendicular to the plane. The transition between these two configurations also depends on the galactocentric distance, and has been invoked in the literature as a possible solution to the CR gradient problem (Cerri et al. 2017).
Starting from the issues discussed above, in this paper we propose a global interpretation of available CR data based on the following assumptions:
-
The spectral steepening in the proton and helium spectra at ∼15 TV, reported by DAMPE, is related to the typical Rmax reached in the acceleration of CRs by the majority of SNRs. Only a fraction of sources, contributing to ≈10 − 20% of the CR population, can accelerate particles up to PeV energies.
-
The propagation of CRs in the GD is assumed to be characterized by inefficient scattering along field lines, assumed to be mostly parallel to the GP, and by a motion perpendicular to the mean field (and disk) dominated by the FLRW induced by the large-scale turbulence in that region. As we show in detail in Sect. 2, if the scattering mean free path is larger than a characteristic length LRR (typically a few times the field coherence length; see Eq. (10)), beyond which a particle trajectory is no longer correlated with its initial field line, the motion perpendicular to the mean field (and so to the GP) is found to be diffusive, roughly rigidity independent, and with an effective diffusion coefficient substantially smaller than that along the field lines.
-
The CR transport in the kiloparsec-scale GH is the typical diffusive motion, with the typical rigidity-dependent diffusion coefficient commonly adopted in a large variety of propagation models.
We show that, with these assumptions, it is possible to reproduce quite well i) the proton and helium spectra from GV to multi-PV rigidities and the p/He ratio; ii) the available spectral data for nuclei ranging from lithium to iron; iii) the p̄ flux and the p̄/p ratio; and iv) the abundance ratios B/C, B/O, C/O, Be/C, Be/O, and Be/B. Moreover, we also discuss the 10Be/9Be ratio in view of the recent AMS02 preliminary measurements.
These results were obtained with a relatively small number of free parameters, without introducing spectral breaks in the injection spectra or in the GH diffusion coefficient. However, similar to previous works (see, e.g., Evoli et al. 2019), the required injection spectra of protons, helium, and heavier nuclei were found to be slightly different: the protons were systematically steeper than nuclei, and helium systematically flatter than protons and nuclei (see Table 1).
Benchmark parameters. Solar modulation potential Φmod = 450 MV.
The paper is organized as follows. In Sect. 2 we discuss the microphysics of the Galactic propagation of CRs and describe the model for the CR transport in the GD. In Sect. 3 we report the details of the proposed CR propagation setup and discuss the analytic solution of the transport equation, which is derived in Appendices B and C. In Sect. 4 we discuss our results and compare our predicted CR fluxes with available data. We draw our conclusions in Sect. 5.
2. Model of cosmic-ray propagation in the disk
The diffusive propagation of CRs in the ISM is dictated by their interaction with the turbulent Galactic magnetic field. The CR random motion is thought to be due to scattering on plasma waves, most notably magnetohydrodynamic (MHD) incompressible Alfvénic and compressible (fast and slow) magnetosonic fluctuations (Mertsch 2020; Lazarian et al. 2023), at the resonant scale λ ∼ rL (even though nonresonant interaction may also be relevant, Lazarian et al. 2023).
Magnetohydrodynamic turbulence is ubiquitous in the interstellar space and is produced by astrophysical sources on scales ≈10 − 100 pc. In order to be able to effectively scatter CRs, this turbulence has to cascade to resonant scales (≪pc for sub-PV particles) without being damped or becoming inefficient for scattering. In particular, a variety of studies showed that the scattering associated with Alfvénic turbulence is highly suppressed due to the anisotropy of the cascade, while magnetosonic modes can play a dominant role in CR diffusion (Fornieri et al. 2021a; Lazarian & Xu 2021; Lazarian et al. 2023). Alternatively, CRs can also produce plasma waves, for example through the excitation of Alfvén waves at the resonant scale (Skilling 1971), although this effect is likely ineffective beyond ≈ a few hundred GeV (Farmer & Goldreich 2004; Aloisio & Blasi 2013). At the same time, turbulence is also subject to a variety of damping processes, such as ion-neutral damping in a partially ionized medium and the nonlinear Landau damping (Recchia et al. 2022). Such effects are typically very important in the GD, while their impact is expected to be less dramatic in the GH (where ion-neutral damping does not operate).
The actual CR transport in a magnetized and turbulent environment is typically much more complex than a purely isotropic diffusive motion and may be anisotropic with respect to the average magnetic field (Mertsch 2020; Shalchi 2020). We assume that a region is embedded with a mean magnetic field B0, and a turbulent field δB(k), with a given spectrum in wave-number k characterized by a maximum (injection) scale Lmax = 1/kmin and a coherence length parallel (L∥) and perpendicular (L⊥) to B0. In the following we assume for simplicity that the turbulence is such that L∥ = L⊥ ≡ Lc. Moreover, we assume that such perturbations are small, namely δB/B0 ≪ L⊥/L∥, a condition likely to be met in the ISM and necessary in order to apply the quasi-linear theory of particle transport (Kadomtsev & Pogutse 1979). The perturbations at the resonant scale, δBres, produce a pitch angle scattering of the particle, which eventually result in a spatial diffusion along field lines, characterized by the parallel diffusion coefficient D∥. This process is typically rigidity dependent as a result of the spectral properties of the turbulence (Mertsch 2020). In the absence of scattering the particles would simply gyrate in the local field.
The particle transport perpendicular to B0 is a combination of the FLRW, namely the stochastic motion of field lines, which is due to fluctuations on a large-scale (much larger than the resonant scale) and of the diffusion across field lines due to particle jumping from one line to another (Rechester & Rosenbluth 1978; Kirk et al. 1996; Shalchi 2020). When δB/B0 ≪ L⊥/L∥, the latter process is highly suppressed and the former can be approximated as a diffusion process characterized by a field line diffusion coefficient Dm.
Both incompressible Alfvénic turbulence and compressive modes can contribute to FLRW (Shalchi 2021), depending on their specific properties and amplitude compared to the mean field. If the power in Alfvén modes is high, while that in compressive modes is substantially lower, CRs would experience at the same time a weak scattering along field lines and an effective FLRW.
Assuming that B0 is along the z-axis and the x − y plane is perpendicular to B0, the meaning of this quantity is that two field lines that at z = 0 pass in the vicinity of a point (x0, y0), are spread over a larger region at position z, whose size is characterized by a Gaussian distribution such that
For a broadband spectrum of turbulence an estimate of Dm is given by (Kadomtsev & Pogutse 1979; Kirk et al. 1996)
where b2 ≡ (δB/B0)2.
In the absence of scattering, the CR gyromotion leads to a motion along B0 with a speed v ≈ c/2 that only depends on the particle pitch angle and not on rigidity. In this limit, in a time t, a particle travels along B0 by z(t)∼v t. At the same time, the FLRW produces a perpendicular displacement
namely a diffusive motion perpendicular to B0 characterized by an effective diffusion coefficient
Instead, in the case of particle diffusion along field lines with parallel diffusion coefficient D∥,  and the perpendicular displacement reads
and the perpendicular displacement reads
with an effective perpendicular diffusion coefficient
This is the compound diffusion regime illustrated by Rechester & Rosenbluth (1978), among others. If a particle follows the same field line indefinitely, then the effective diffusion coefficient perpendicular to the average field,  vanishes as t increases.
vanishes as t increases.
However, small motions perpendicular to the field lines can restore the diffusive behavior of particles because of the exponential divergence of neighboring field lines (Jokipii & Parker 1969; Rechester & Rosenbluth 1978). The separation d between two neighboring lines increases on average with the distance along the field line as
where Lk is the Lyapunov length. Estimates of Lk gives Lk ≈ Lc (see Chandran 2000 and references therein).
Consider a particle moving along a given field line. A small perpendicular displacement d0 (e.g., induced by field gradients and scattering) brings the particle to a new close-by field line. After traveling a distance
along this new field line, the particle would reach a perpendicular distance Lc from its initial field line. The Rechester-Rosenbluth distance LRR (Rechester & Rosenbluth 1978; Chandran 2000) represents the distance along the new field lines beyond which the particle trajectory is no longer correlated with its initial field line. This means that beyond LRR, even if the particle is scattered back, it will not retrace its original path and it will drift across field lines moving on an new path, uncorrelated with the original one. This loss of correlation allows the particles to escape the regime of compound diffusion.
The effective diffusion coefficient perpendicular to the mean field is given by
where (ΔR)2 is the rms displacement perpendicular to the average field during each statistically independent random step, corresponding to a parallel motion by LRR. If the scattering mean-free path, λmfp (see Eq. (37)), associated with D∥ is λmfp ≪ LRR, for example in the case of effective scattering, we get
specifically
If the scattering mean-free path, λmfp ≳ LRR, for example in the case of inefficient scattering, we get
specifically
which is the same value obtained in the assumption of a pure gyromotion (see Eq. (6)). The value of LRR depends on a variety of parameters, and in particular on the type and level of turbulence, and is typically found to be on the order of a few times Lc (Casse et al. 2001; Chandran 2000).
Interestingly, a flat (or very weak) rigidity dependence of D⊥ in the case of very weak or absent parallel scattering has also been found in simulations (see, e.g., Snodin et al. 2022; Pezzi & Blasi 2024). In particular, Snodin et al. (2022) investigated the limit of λmfp ≫ L∥ and confirmed a very weak dependence of D⊥ when L∥ = L⊥, δB/B0 ≲ 1 and rL < L⊥, under the same assumptions made here.
When particles are released in a turbulent field, an effective isotropic diffusion process, with D = D∥/3 (Casse et al. 2001; Subedi et al. 2017) may be reached due to a combination of parallel diffusion and perpendicular motion, on scales much larger than the field coherence length(s) and on sufficiently long timescales. Such effective isotropic diffusion is likely achieved by CRs in the GH, a region whose size is typically much larger than Lc and where particles can be effectively scattered with little damping of plasma waves (e.g., due to a fully ionized medium). This is also in good agreement with the standard picture of Galactic CR propagation described in the Introduction.
For the GD, the situation is much less clear. On the one hand, effective damping processes (Recchia et al. 2022) may make scattering in the GD ineffective, either preventing the cascade to resonant scales and/or hampering turbulence that is produced already at such scales. This was recognized in pioneering works on CR propagation (Skilling 1971) where the near-disk region was assumed to contain little resonant waves. Particles were assumed to free-stream in this region, while the ionized GH was considered as the actual scattering region. On the other hand, supernova explosions, massive star winds and other astrophysical phenomena may be able to keep some level of resonant waves, or even fill the GD with highly turbulent regions where the diffusion coefficient can be much smaller than in the GH (Jacobs et al. 2023). In many works, CR propagation in the GD is either assumed to proceed with the diffusion coefficient of the GH (in this case the finite size of the disk affects the results at low energies) or the disk is treated as a passive target where particles undergo free-streaming. On the other hand, a variety of works also considered the possibly different diffusion coefficients in the disk and halo (see, e.g., Dogiel et al. 2002; Tomassetti 2015; Zhao et al. 2021).
Here we propose a picture of the CR transport in the GD based on the following assumptions:
-
Particle scattering is ineffective in the GD due to strong wave damping (and/or to the low power of compressive modes, Fornieri et al. 2021a; Lazarian & Xu 2021), so that the scattering mean free path along the GP is λmfp ≳ LRR ;
-
Particle transport perpendicular to the GD mostly takes place perpendicular to the average Galactic magnetic field and is dominated by turbulence on scales much larger than rL.
The second hypothesis is motivated by the observation that large-scale Galactic magnetic field in the disk is mainly parallel to the GP, while in the halo it is preferentially perpendicular to the GP (see, e.g., Pshirkov et al. 2011). With a mean field preferentially parallel to the GP plane, CRs in the GD have to move perpendicular to the field lines in order to enter the GH.
As shown in the discussion above, in this scenario the global CR propagation in the GD perpendicular to the GP can be treated as an effective rigidity-independent diffusion, regulated by the field line diffusion coefficient Dm, as illustrated in Eq. (13). As reported in Table 1, in Eq. (4) we adopt Lc = 10 pc and b2 = 0.4, which corresponds to Dm = 1 pc, namely  . Considering that LRR is a few times Lc, we assume as reference values LRR ∼ 50 − 100 pc.
. Considering that LRR is a few times Lc, we assume as reference values LRR ∼ 50 − 100 pc.
Interestingly, such effective diffusion would correspond to a residence time in the GD on the order of
a value close to that found in Eq. (2) from the B/C at ≈ 1 TeV/n. The superscript “min” has been added in the definition of residence time provided in Eq. (14) to indicate that this is indeed a minimum value for such physical quantity. It corresponds to the residence time of particles that cross diffusively the disk once, and after entering the halo they diffusively escape from the Galaxy without ever returning to the disk. The corresponding minimum (and rigidity-independent) grammage is then
This is the grammage experienced by particles of large enough rigidity, which diffuse fast enough in the halo (the diffusion coefficient in the GH increases with R) to never come back to the disk.
At the same time, CRs experience a much larger diffusion coefficient along the GP, with λmfp ≳ LRR. Taking LRR ∼ 50 − 100 pc, λmfp ≳ 50 − 100 pc implies  . Such values are compatible with scattering on compressive modes characterized by an injection scale L ∼ 10 pc, δB/B0 ≲ 0.1 and a plasma β ∼ 0.1 (see Fornieri et al. 2021a and references therein). Thus, during the time τdmin, CRs would cover a distance d∥ along the plane:
. Such values are compatible with scattering on compressive modes characterized by an injection scale L ∼ 10 pc, δB/B0 ≲ 0.1 and a plasma β ∼ 0.1 (see Fornieri et al. 2021a and references therein). Thus, during the time τdmin, CRs would cover a distance d∥ along the plane:
3. Propagation setup
In this section we present steady-state solutions of the transport equation for CR nuclei in the GD and GH. We consider a 1D problem along the coordinate z directed orthogonally to the GD and centered on it. In the GH this description is justified by our assumption that field lines are preferentially perpendicular to the GP. Moreover, a weak dependence on the radial coordinate is also confirmed by the small CR anisotropy and by the small CR gradient along the GP, as inferred from γ-ray observations (see, e.g., Evoli et al. 2019). In the GD, a 1D description is justified by our assumption that the particle motion perpendicular to the GP is much slower than along the plane, in line with the small radial CR gradient. We provide in the following a detailed description of the propagation setup, which is also illustrated in Fig. 3.
 |
Fig. 3. Schematic representation of the propagation setup. The size of the GD (violet region) is h ∼ 150 pc and the magnetic field lines are preferentially parallel to the GP. The CR transport perpendicular to the plane is dominated by the large-scale turbulence and is encompassed in the rigidity-independent diffusion coefficient Dh; the size of the GH (gray region) is H ∼ 4 kpc and the magnetic field lines are preferentially perpendicular to the GP. The CR transport perpendicular to the plane is dominated by resonant scattering on plasma waves, encompassed in the rigidity-dependent diffusion coefficient DH, plus the contribution of advection in a wind of velocity u. |
3.1. Transport equation
We consider the phase-space density of CRs fα(z, p) as a function of the particle momentum p and position z for a nucleus of species α of mass number Aα and atomic number Zα. Since the kinetic energy per nucleon, Ek, is roughly conserved in the spallation processes, we express the transport equation in terms of the particle flux Iα(z, Ek) = Aα c p2fα(z, p), where  (Bresci et al. 2019):
(Bresci et al. 2019):
The first term on the left-hand side describes diffusive-advective transport while the second represents the adiabatic losses. The first term on the right-hand side describes the radioactive decay (relevant for 10Be), the second term the spallation of nucleus α to lighter nuclei, the third the injection from SNRs and other astrophysical sources, and the fourth the contribution to nucleus α from the spallation of heavier nuclei β. In order to simplify the solution of the transport equation, we assume that the particle injection from sources and the spallation or production of nuclei take place in a very thin gaseous disk (hydrogen density nd = 1 cm−3, half-height hd = 15 pc, radius Rd = 15 kpc), so that the corresponding terms in the transport equation can be approximated with a delta function, ∝δ(z). In Eq. (17), we neglect ionization losses since they are relevant only at R≲ a few GV (Evoli et al. 2019 and references therein), where the observed spectrum is largely affected by the solar modulation (see Sect. 4).
3.2. Injection spectrum
The injection spectrum  of a nucleus α from a given class i of astrophysical sources is modeled as a power law (in rigidity-momentum) plus cutoff at given rigidity Rmax, i,
of a nucleus α from a given class i of astrophysical sources is modeled as a power law (in rigidity-momentum) plus cutoff at given rigidity Rmax, i,
where ϵαLi the fraction of average source luminosity channeled to CR nuclei of type α, and ![$ \mathcal{G}(\gamma) = 4\pi\int_0^{\infty} dx x^{2-\gamma}\exp^{-x/x_{max}}\left[ \sqrt{x^2+1} -1 \right] $](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq37.gif) is a normalization factor. The quantity ϵα is determined by fitting the AMS02 flux for the given nucleus at a reference rigidity (e.g., R = 50 GV).
is a normalization factor. The quantity ϵα is determined by fitting the AMS02 flux for the given nucleus at a reference rigidity (e.g., R = 50 GV).
Following the discussion in Sect. 1, we assume that the bulk of CRs are accelerated in typical SNRs, up to a typical cutoff rigidity  , chosen in order to reproduce the spectral steepening found in the DAMPE data (An et al. 2019; Alemanno et al. 2021) in the multi-TV range. The injection spectrum for such population is given by
, chosen in order to reproduce the spectral steepening found in the DAMPE data (An et al. 2019; Alemanno et al. 2021) in the multi-TV range. The injection spectrum for such population is given by
where  and
and  are the total explosion energy and rate of SNe, respectively.
are the total explosion energy and rate of SNe, respectively.
We then assume that only a subclass of sources can accelerate particles up to PeV energies. We model the spectrum of CRs injected by this population as
in other words, we assume the slope to be the same for the two populations, but we here set 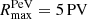 and we add a normalization factor equal to
and we add a normalization factor equal to  of the overall energy input of typical SNRs.
of the overall energy input of typical SNRs.
The total injection spectrum is then given by
3.3. Spallation and production cross section
We assume that CR nuclei interact with the ISM medium, made mostly of hydrogen (H) and a fraction fHe ≈ 10% of helium (He).
For the total spallation cross section,  , of CR nuclei heavier than He, we adopt the parameterization by Tripathi et al. (1999), described in detail by Evoli et al. (2018b) and also implemented in DRAGON-II1 and USINE2 (Maurin 2020). For the He nuclei we adopt the cross sections reported by Coste et al. (2012).
, of CR nuclei heavier than He, we adopt the parameterization by Tripathi et al. (1999), described in detail by Evoli et al. (2018b) and also implemented in DRAGON-II1 and USINE2 (Maurin 2020). For the He nuclei we adopt the cross sections reported by Coste et al. (2012).
For the production cross section,  , in general we adopt the OPT22 parameterization available from the GALPROP code3 (Porter et al. 2022), making use of the tables provide in the USINE code. For the channel 4He → 3He we use the cross section reported by Coste et al. (2012). Limited to the production of Li, Be, and B by CNO nuclei, we adopt the results by Evoli et al. (2019), using the tables reported in the DRAGON-II code.
, in general we adopt the OPT22 parameterization available from the GALPROP code3 (Porter et al. 2022), making use of the tables provide in the USINE code. For the channel 4He → 3He we use the cross section reported by Coste et al. (2012). Limited to the production of Li, Be, and B by CNO nuclei, we adopt the results by Evoli et al. (2019), using the tables reported in the DRAGON-II code.
In is important to note that the energy-dependent production of a given nucleus by the spallation of heavier nuclei is affected by rather large uncertainties, typically on the order of ∼20%, but often even larger. These uncertainties are related to the quality and amount of data (if available) for a given production cross section, and to the difficulty in assessing the contribution of all possible production channels, including that of ghost nuclei (short lived isotopes). A detailed discussion of this issue is beyond the scope of the present paper, and we refer to the excellent works by Génolini et al. (2018), Evoli et al. (2019) and Génolini et al. (2024).
3.4. Antiprotons
The production of secondary p̄ in the interaction of CR protons and He with the ISM (H and He target) is treated following Korsmeier et al. (2018). In this case, the last term of Eq. (17) can be rewritten as
Here  is the p̄ source term,
is the p̄ source term,
where Ek and Eki are respectively the kinetic energy per nucleon of the p̄ and of the incoming CR, Ii(Eki) is the incoming CR flux, fj = 1(0.1) for the H(He) target, and  is the differential production cross section, which is provided in tabular form in the supplemental material of Korsmeier et al. (2018).
is the differential production cross section, which is provided in tabular form in the supplemental material of Korsmeier et al. (2018).
For the quantity σα(Ek) of Eq. (17), we use the total inelastic cross section for the  interaction, that can be computed as the difference between the total and elastic cross sections provided by Workman et al. (2022).
interaction, that can be computed as the difference between the total and elastic cross sections provided by Workman et al. (2022).
3.5. Diffusion and advection
We define the diffusion coefficient and advection velocity in the GD (subscript h) and GH (subscript H) as
The GD is assumed to have half-height h = hd = 150 pc, and the transport of particles there is rigidity-independent, with the diffusion coefficient  defined in Eq. (13). We note that the size of the GD and of the gaseous disk do not necessarily need to coincide, but we make this assumption here for simplicity.
defined in Eq. (13). We note that the size of the GD and of the gaseous disk do not necessarily need to coincide, but we make this assumption here for simplicity.
The GH is assumed to have a half-height H = 4 kpc, the Galactic wind speed there is u = 40 km/s, and the particle (rigidity-dependent) diffusion coefficient is set equal to
with D0 = 1028 cm2/s and δ = 0.7.
Beyond a distance z = H + h ≡ H* from the GP, CRs are assumed to free escape:
3.6. Analytic solution for stable nuclei
In Appendices B and C we derive the analytic solution of Eq. (17) in the disk, Iα0(Ek), in the case of stable and unstable nuclei, with the conditions specified in Eqs. (24, 25, 27), and neglecting adiabatic losses (see Appendix A for a discussion).
Here we report the solution for stable nuclei and discuss its main characteristics:
Here
are the injection from sources and the injection from spallation of heavier nuclei (per ISM atom), respectively.
The term  can be interpreted as the residence time in the GD, due to diffusion in the GD itself and to the repeated crossings of the region induced by scattering in the GH, and reads
can be interpreted as the residence time in the GD, due to diffusion in the GD itself and to the repeated crossings of the region induced by scattering in the GH, and reads
We also define the grammage
and the critical grammage Xcr α ≡ μ/σα, where μ = 1.4mp is the mean mass of the ISM gas. The term nd hd/h represents the ISM density averaged over the GD.
In terms of the grammage, Eq. (28) can be rewritten as
The solution can be understood as follows. We consider the case of CR protons, which are purely primary and for which σα = 0. The flux of Eq. (28) becomes
which is the same solution found in Eq. (A.10) when adiabatic losses are neglected. Considering that DH ∝ Rδ increases with rigidity, while Dh is assumed to be constant, the residence time in the GD of Eq. (30) is expected to be dominated by diffusion in the GD at high enough rigidity, such that h/Dh > H/DH (i.e., above the transition rigidity):
The value of R* depends on the relative size of the GD and GH, on Dm, and on the normalization and slope of DH. Taking the reference values reported in Eq. (34), the transition is expected at
-
≈6 TV (δ = 0.5),
-
≈2 TV (δ = 0.6),
-
≈500 GV (δ = 0.7),
-
≈200 GV (δ = 0.8).
Thus, if the slope of the diffusion coefficient in the GH is δ ≳ 0.6 (Evoli et al. 2019), as typically found in models of self-generated diffusion (Aloisio & Blasi 2013), at R ≳ 100 s GV − TV the effect of propagation on the CR distribution in the disk smoothly becomes independent of rigidity. Correspondingly, the grammage would tend to the constant minimum value reported in Eq. (15) (in the assumption that h = hd)
Below R ∼ R*, the residence time in the GD is dominated by the repeated crossings due to diffusion in the GH, with a contribution of advection, which typically dominates at R ≲ 10 GV. The advective (uH ≫ DH) and diffusive (uH ≪ DH) limiting cases read
similar to what is described in Appendix A.
As a final remark, it is important to note that the diffusion equation in the GH is valid only up to a rigidity, RHmfp, such that the diffusive mean free path is smaller than the size of the diffusive halo, namely λmfp ≲ H, where
which gives
For δ = 0.5 − 0.8 the value of Rmfp, H reads
-
≈150 PV (δ = 0.5),
-
≈6 PV (δ = 0.6),
-
≈700 TV (δ = 0.7),
-
≈100 TV (δ = 0.8).
Thus, at high enough rigidity, particles in the GH do not really diffuse, but rather free-escape. We treat this case by performing the limit H → 0 in Eq. (28), which corresponds to moving the free-escape boundary H* → h. On the other hand, for the cases treated in this work, R* ≪ RHmfp, and thus the solution at R ≳ RHmfp would be largely dominated by the diffusion in the GD even without performing the limit H → 0.
4. Results
In this section we describe the main results of our calculations. The CR fluxes are evaluated using Eq. (28), with the setup illustrated in Sect. 3.
For the injection spectrum of Eq. (21) we assume the slope γp = 4.35 for protons, γHe = 4.3 for He and γn = 4.33 for all the other nuclei. We note that different slopes for the injection spectra of p, He, and heavier nuclei, with γp > γn > γHe, were also used in other works aimed at fitting CR spectra (see, e.g., Aloisio & Blasi 2013; Bresci et al. 2019; Evoli et al. 2019). While possible explanations based on the subtleties of the DSA process have been put forward (see, e.g., Malkov et al. 2012), this difference is currently an open issue and discussing it goes beyond the scope of the present work.
The effect of the solar modulation is accounted for in the force-field approximation (Gleeson & Axford 1968), with a modulation potential Φmod = 450 MV. The relevant physical parameters adopted in the calculations are summarized in Table 1.
Before proceeding to a detailed description of our results, two remarks are in order. First of all, since the main purpose of this work is to show the plausibility of the proposed scenario on a large variety of CR data, we did not attempt an accurate fitting procedure on the data, which is deferred to a future work. Here instead we looked for a qualitatively good agreement with data. In that sense, the parameters reported in Table 1 should not be intended as best-fit values, but as a benchmark setup.
Second, while in general we obtain a good agreement with data (in the sense described above) at rigidity R ≳ 10 GV, in the low-rigidity domain the agreement tends to be poorer, although quite decent in most cases. A proper estimate of the CR fluxes at low rigidities should consider ionization losses, and a more refined modeling of advection with the inclusion of adiabatic losses. Moreover, in order to keep the number of free parameters limited, we calculated the solar-modulated spectra with the same Φmod for all nuclei. However different data sets were collected at different times, so that using a slightly different value of the modulation potential for different data sets may also affect the agreement with data at low rigidity.
On the other hand, the scenario proposed in this work substantially differs from the standard CR propagation paradigm beyond R ≳ 100 GV. For this reason, we decided to leave out the above-mentioned effects and to treat low-rigidity CRs in a simplified way. We defer a more refined calculation and a best-fit analysis of the proposed scenario to a future work.
4.1. Protons, helium, and antiprotons
In Fig. 4 we show the proton and He fluxes (made mostly of 4He with a fraction of secondary 3He produced by the spallation of 4He; see, e.g., Coste et al. 2012) in the range 1−105 GV and the corresponding p/He ratio. These spectra can be understood with the help of Fig. 5. At R ≲ 10 GV the (unmodulated) solution is dominated by advection, as indicated by the flattening in the grammage (see Fig. 5). As illustrated in Appendix A, this results in a hardening of the CR flux at low R.
 |
Fig. 4. Proton and helium fluxes in the range 1 − 105 TV. Top panel: Unmodulated (solid orange) and modulated (dashed red) proton flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2022, blue squares), CREAM (Yoon et al. 2017, magenta diamonds), and DAMPE (An et al. 2019, cyan triangles). Middle panel: Unmodulated (solid orange) and modulated (dashed red) He flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2023, blue squares), CREAM (Yoon et al. 2017, magenta diamonds), and DAMPE (Alemanno et al. 2021, cyan triangles). Bottom panel: p/He flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2023, blue squares), and NUCLEON (Karmanov et al. 2020, green points). |
In the range R ≈ 10 − 100s GV the CR flux is mostly affected by the steep rigidity-dependent diffusion in the GH, DH ∝ R0.7, which is reflected in the power-law drop in the grammage. On the other hand, above a few hundred GV, the grammage smoothly begins to flatten, as described in Sect. 3.6, leading to a gentle progressive hardening of the CR spectrum, in good agreement with the data. Such smooth flattening of the spectrum is the result of the h/Dh term in Eq. (30) becoming comparable to and then larger than H/DH with the increase in R, a transition that takes place in ≈1 − 2 decades in R around ≈ 1 TV.
It should be noted that the slope of the grammage reported in Fig. 5 is ∼0.33 at ≈400 GV and ∼0.3 at ≈1 TV. This explains, at least qualitatively, why we find a good agreement with the data below a few TV with injection spectra with slopes ≈4.3, in line with previous works that find best fits with a similar injection and a Kolmogorov-like diffusion at high energy (see, e.g., Evoli et al. 2020).
The spectral steepening at ≈ 15 TV reported by DAMPE is the result of the majority of SNRs accelerating particles with a typical cutoff rigidity  . Such steepening can also be identified in the Cosmic Ray Energetics and Mass Experiment (CREAM) and CALET data for the p spectrum, while in the case of He the situation is less clear, especially due to the quite large discrepancy between the spectra reported by the three experiments.
. Such steepening can also be identified in the Cosmic Ray Energetics and Mass Experiment (CREAM) and CALET data for the p spectrum, while in the case of He the situation is less clear, especially due to the quite large discrepancy between the spectra reported by the three experiments.
In general, we obtain a very good agreement with both AMS02 and DAMPE data for p and He in the whole 1−105 GV range, and in particular at R ≳ 10 GV, where solar modulation is unimportant. Our prediction for the p/He ratio closely matches the AMS02 data at R ≲ 1 TV and the NUCLEON data at higher R. Also in this case the different data sets show relevant discrepancies in the multi-TV range.
In Fig. 6 we show the proton and He fluxes of Fig. 4, as a function of the total energy ETOT, in the range 103 − 108 GeV. The red curve corresponds to the expected contribution from the two classes of sources described in Sect. 3 (i.e., typical SNRs with a cutoff rigidity at  see Eq. (19), and PeV sources characterized by
see Eq. (19), and PeV sources characterized by  see Eq. (20)), and represents the very high-energy part of the fluxes shown in Fig. 4. The CR luminosity of the PeV population is
see Eq. (20)), and represents the very high-energy part of the fluxes shown in Fig. 4. The CR luminosity of the PeV population is  times that of the bulk population.
times that of the bulk population.
 |
Fig. 6. Proton fluxes (left panel) and He fluxes (right panel) compared to the data of DAMPE (An et al. 2019; Alemanno et al. 2021, cyan triangles), NUCLEON (Grebenyuk et al. 2019a, green points), Icecube-Icetop (Aartsen et al. 2019, orange diamonds), KASCADE (Antoni et al. 2005, pink and violet points), and KASCADE-Grande (Arteaga-Velázquez et al. 2017, yellow points). The red curves correspond to the case with two source populations. The blue curves correspond to the case of a source CR luminosity decreasing with the increase in maximum rigidity. |
As a comparison, we also show the case (blue curve) of a uniform distribution of ln(Rmax), in the range  , with an overall CR luminosity linearly decreasing with ln(Rmax) compared to the bulk of sources, in the range
, with an overall CR luminosity linearly decreasing with ln(Rmax) compared to the bulk of sources, in the range  . The injection spectrum in this case can be written as
. The injection spectrum in this case can be written as
where q0, αi is defined in Eq. (18),  , ϵi(lmax) Lbulk is the luminosity for a given lmax, with
, ϵi(lmax) Lbulk is the luminosity for a given lmax, with
Keeping in mind the quite large systematics between the different data sets, especially in the multi-PeV domain, we can see that our model is able to reproduce the data quite well, from R ≳ 10 GV up to the multi-PV domain.
This result is the combination of the rigidity-independent propagation experienced by CRs beyond ≈ 10 TV (see Fig. 5) and of the smaller CR luminosity of sources able to reach very high energies compared to that of the majority of sources, although the current data do not allow a clear discrimination between a two-population scenario and a distribution of Rmax with a progressive decrease in the CR luminosity. It is important to note that, in the presented scenario, it is not necessary to assume a different slope for the two source populations (or a dependence of the slope on Rmax), and indeed we obtained the reported fluxes with a fixed slope for a given species (p or He; see Table 1).
If we assumed that the bulk of SNRs accelerate particles up to the knee, with a rigidity-independent propagation, at such high energies we would get a very hard CR spectrum that would largely overshoot the data. In order to explain the steepening in the DAMPE data without affecting the CR flux at lower energies, we would be forced to introduce a change in the propagation regime at R ≈ 20 TV in addition to that required to explain the hardening at R ≈ 300 GV.
Instead, if we assume a propagation model such that the rigidity dependence of the grammage is the same as in Fig. 5 up to R ≈ 1 TV and steeper at higher R, for example the typical ∝R0.3 of a Kolmogorov turbulence invoked at high energies by previous works (see, e.g., Aloisio & Blasi 2013; Evoli et al. 2018a), the predicted spectra would lie below the DAMPE and NUCLEON data.
In Fig. 2 we show our prediction for the p̄ flux and for the p̄/p ratio compared to the AMS02 data. In order to highlight the typical uncertainty in the production cross section of p̄ (Korsmeier et al. 2018), we placed a 10% (yellow) and 20% (green) band around our predicted flux. For both quantities we obtain excellent agreement with the data. In particular, we reproduce well the quite flat p̄/p ratio that typically fails to be explained in standard propagation scenarios.
This result can be explained as follows. First, the antiprotons produced in p-p collisions (with a nonnegligible contribution from p-He, He-p, and He-He channels; see Korsmeier et al. 2018) have broad energy distributions. The kind of kinematics involved in the process significantly reshapes the p̄ production spectrum  , making it appreciably harder than the parent p (and He) flux. This can be seen in Fig. 2, where we show (in the bottom left panel) the
, making it appreciably harder than the parent p (and He) flux. This can be seen in Fig. 2, where we show (in the bottom left panel) the  corresponding to the p̄ flux shown in the upper left panel of the same figure, and in the bottom right panel we report their slopes. Second, antiprotons propagate in the ISM as protons (apart for the role played by the spallation of p̄) so that the slope of the equilibrium spectrum of antiprotons we expect
corresponding to the p̄ flux shown in the upper left panel of the same figure, and in the bottom right panel we report their slopes. Second, antiprotons propagate in the ISM as protons (apart for the role played by the spallation of p̄) so that the slope of the equilibrium spectrum of antiprotons we expect  , as is indeed observed (see bottom right panel of Fig. 2). The combination of a hard
, as is indeed observed (see bottom right panel of Fig. 2). The combination of a hard  and of the progressive flattening of the grammage X keeps
and of the progressive flattening of the grammage X keeps  in the range R = 30−1000 GV, which translates in a very mild decrease in the p̄/p ratio in such rigidity range.
in the range R = 30−1000 GV, which translates in a very mild decrease in the p̄/p ratio in such rigidity range.
4.2. LiBeB and CNO nuclei
In the left panels of Fig. 7 we show the C, N, and O fluxes. O (mostly 16O, 17O,18O) and C (mostly 12C, 13C) are mainly primary, with a fraction of a few percent and ≲20%, respectively, of secondary contribution from heavier nuclei at low rigidity. Most of the secondary C is due to the spallation of O. For both nuclei we reproduce well the AMS02 data. In addition, the progressive transition to a flat grammage, described above, produces a rather hard spectrum beyond ∼ TV rigidity, in agreement with the CREAM and NUCLEON experiments. We note, however, the sizable discrepancies between data sets at high-R. The C/O ratio is also in good agreement with the AMS02 data, as shown in Fig. 1.
 |
Fig. 7. LiBeB and CNO nuclei. Top left panel: C flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2020, blue squares), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). Center left panel: N flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CREAM (Ahn et al. 2009, magenta diamonds). Bottom left panel: O flux compared to the data of AMS02 (Aguilar et al. 2021d, 2023, black dots and yellow diamonds), CALET (Adriani et al. 2020, blue squares), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). The solid red line corresponds to the total modulated flux, while the solid blue line to the (modulated) secondary contribution to the given nucleus. The cyan (blue) shaded region corresponds to a 10% (20%) uncertainty in the secondary production cross section, which translates in the yellow (green) shaded region in the total flux. Right panels: Li, Be, and B fluxes compared to the data of AMS02 (Aguilar et al. 2021d, black dots) and CALET (Adriani et al. 2020, blue squares). The solid red line corresponds to the total modulated flux. The yellow (green) shaded region corresponds to a 10% (20%) uncertainty in the secondary production cross section. The solid blue line corresponds to the total flux multiplied by fLi = 0.92 (Li), fBe = 0.9 (Be) and fB = 1.1 (B). |
Nitrogen (14N, 15N) is partially primary and partially secondary (with a major contribution from the spallation of O). Also in this case we get a good agreement with the AMS02 data, and in particular, we reproduce the rather sharp high-R hardening of the spectrum. We also note that the multi-TV flux is affected by the uncertainty (typically ≈20%) in the secondary production cross section. We normalize the injection spectrum of N from sources in order to reproduce the observed AMS02 flux at 50 TV. A 10% (cyan) and 20% (violet) uncertainty in the secondary production translates in a re-normalization of the primary contribution in order to get the same flux at 50 TV, which clearly appears in the yellow and green bands at multi-TV (where the primary part largely dominates).
In the right panels of Fig. 7 we show the Li (6Li, 7Li), Be (7Be, 9Be, 10Be), and B (10B, 11B) fluxes. The contribution 11B from the shot-lived isotope 11C is also included (see Evoli et al. 2019). The red curves are the fluxes obtained with the production cross sections specified in Sect. 3, with the yellow and green band representing a 10% and 20% uncertainty in the production cross sections, respectively. The main production channels (≳80% at Ek ≳ 10 GeV/n) come from the spallation of CNO nuclei. As discussed in detail by Evoli et al. (2019), the cross sections are quite uncertain, especially at Ek ≳ 10 GeV/n, due to the fact that most of experimental data are usually at hundreds of MeV/n, and only some channels are probed at a few GeV/n. The channels CNO → LiBeB, reported in the Appendix of Evoli et al. (2019), show a typical uncertainty of 20 − 30%, and in some channels they can exceed ∼50%, such as 16O → 7Li, 9Be. Moreover, the channels 14N → 6Li, 7Li, 9Be, 10B, 11B, have only one or two data points below ∼ 1 GeV/n, thus making the high-energy cross sections even more difficult to determine. Additional uncertainties come from the LiBeB production from heavier nuclei. Finally, the systematic uncertainties related to the available measurements and the contribution of ghost nuclei are difficult to asses.
With the adopted cross sections we get Li, Be, and B fluxes whose shapes are in good agreement with the AMS02 data; in particular, we reproduce quite well the progressive flattening around ≈ TV. However, our Li and Be fluxes are systematically higher than the data and our B flux is systematically lower. Keeping in mind the large uncertainties in the production cross sections, we also show (blue lines) the Li flux multiplied by fLi = 0.92, the Be flux multiplied by fBe = 0.9, and the B flux multiplied by fB = 1.1, which match the AMS02 data well.
With such re-normalization we also find a very good agreement with the AMS02 data for the B/C and B/O ratio (Fig. 1) and with the AMS02 data for the Be/C, Be/O, and Be/B ratio (Fig. 8). We note in particular the high-R flattening of the B/C related to the flattening of the grammage.
 |
Fig. 8. Be/C (top left panel), Be/O (top right panel), and Be/B (bottom left panel) ratios (red solid line) compared to the data of AMS02 (Aguilar et al. 2018, 2021d, black dots). The green shaded region corresponds to a 20% uncertainty in the secondary production cross section. The solid blue line corresponds to the Be/C, Be/O, or Be/B ratio when the Be flux is multiplied by fBe = 0.9 and the B flux by fB = 1.9, as in Fig. 7. The 10Be/9Be ratio (bottom right panel) is compared to the preliminary AMS02 data (black dots) and to the data of a variety of other experiments, collected from the Cosmic-Ray Database (Maurin et al. 2023). The solid red line corresponds to a GH size of H = 4 kpc. The yellow, green, and pink shaded regions corresponds to a 10%, 20%, and 30% uncertainty in the production cross section, respectively. The solid cyan and purple lines correspond to H = 6 kpc and H = 8 kpc, respectively. |
We note however, in the case of B, that a caveat should be taken into account. Indeed, 10B receives a contribution from the decay of 10Be (see discussion below), which, contrary to the contribution from spallation, is not concentrated in the disk, but is spatially extended, as discussed in detail in Evoli et al. (2020). On the other hand, the relevance of this contribution to the B flux can be estimated by comparing, in Fig. 4 of Evoli et al. (2020), the dotted line that corresponds to the case of assuming a stable 10Be, and the Be/B data. That figure shows that the effect is expected to reach a maximum at ∼10 GV, and that it becomes completely irrelevant beyond 100 GV. Moreover, it can be shown that ignoring the contribution from the decay of 10Be modifies the spectrum of B at 10 GV by less than 10%. This is at the level of, or even smaller than, the typical uncertainties in the production cross sections. For this reason, in order to keep the calculation simpler, we neglected this term.
10Be is a long-lived unstable isotope (half-life of 1.39 Myr) which is of great importance in determining the CR residence time in the Galaxy. In Appendix C we derive the solution of the transport equation in the case of unstable isotopes, in the same GD-GH setup adopted in the case of stable isotopes.
The relevance of 10Be in the estimate of the halo size can be understood from the limiting case of a single halo, as derived in Appendix C. In this limit, the flux of unstable isotopes scales as
where τdiff = H2/D is the diffusion timescale and τr is the decay timescale. We note that the former limit corresponds to the case of stable isotopes, and is reached at high enough energy, since the decay time increases with the total energy, τr ∝ E. Thus, the flux of stable isotopes is sensitive to the ratio H/D and not to the two quantities separately. Instead, measuring unstable isotopes, or the ratio of stable to unstable isotopes of the same nucleus, provides additional information that allows the value of H to be determined. The ratio of 10Be to the stable isotope 9Be tends to
In Fig. 8 we show our prediction for the 10Be/9Be, with the benchmark parameters reported in Table 1, and in particular for H = 4 kpc (red curve), compared to preliminary recent AMS02 data and to a variety of other data (Maurin et al. 2023). We also consider the large uncertainties in the production cross sections discussed above, and show the change in the ratio when the cross section for each isotope separately is increased or decreased by 10% (yellow), 20% (green), and 30% (pink). Given the large spread of data at low Ek, our benchmark result is compatible with this data, but is substantially larger than the AMS02 data. While the uncertainty in the cross section may ease the mismatch, a better agreement with the AMS02 data can be achieved by increasing the halo size to H = 6 − 8 kpc, as shown by the cyan and purple curves (see also the discussion in Jacobs et al. 2023). It should be noted that, considering the caveats related to our treatment of low-rigidity CRs and to our neglect of the spatially extended decay of 10Be to 10B, the estimate of the halo size should not be considered as a best fit, but rather as a plausible range in the presented framework.
All other fluxes will not be affected by a rescaling of H → x H provided that (keeping h and DH fixed)
-
nd → nd/x,
-
Dh → Dh/x,
-
u → u/x.
4.3. Heavy nuclei
In Fig. 9 we show our results for the Ne, Mg, Si, and Fe fluxes. For Fe we consider only the isotope 56Fe and we treat it as purely primary. In general, always keeping in mind the discrepancies between the data sets, we obtain a quite good agreement with both the AMS02 and NUCLEON data, except for the case of Fe, where the NUCLEON data are systematically well below the AMS02 data. A ≈20% uncertainty on the production cross sections should also be accounted for (Génolini et al. 2024). Moreover, the secondary contribution to these nuclei (blue curve in the plots) may be somewhat underestimated, considering that many fragmentation channels are involved starting from 56Fe and the possible (unknown) systematics related to each channel. For instance, a better agreement with data can be obtained in the case of Si and Mg by multiplying the secondary flux by 1.2 and 2, respectively, and changing the primary flux accordingly (green dashed line).
 |
Fig. 9. Ne, Mg, Si, and Fe modulated fluxes (red solid line) and their secondary component (blue solid line). Top left panel: Ne flux compared to the data of AMS02 (Aguilar et al. 2021d, 2023, black dots, yellow diamonds), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). Top right panel: Mg modulated flux compared to the data of AMS02 (Aguilar et al. 2021d, 2023, black dots, yellow diamonds), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). The dashed green line is obtained by multiplying the secondary component by 2. Bottom left panel: Si flux compared to the data of AMS02 (Aguilar et al. 2021d, 2023, black dots, yellow diamonds), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). The dashed green line is obtained by multiplying the secondary component by 1.2. Bottom right panel: Fe flux compared to the data of AMS02 (Aguilar et al. 2021a, black dots), CALET (Adriani et al. 2021, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). |
In Fig. 10 we show the F, Na, Al, and S fluxes compared to AMS02 data. Considering the uncertainties in the production cross sections, particularly relevant for the predominantly secondary F, we reproduce the data quite well.
 |
Fig. 10. F, Na, Al, and S modulated fluxes. Top left panel: F modulated flux (red solid line) compared to the data of AMS02 (Aguilar et al. 2021b, 2023, blackdots, yellowdiamonds). Top right panel: Na modulated flux (red solid line) and its secondary component (blue solid line) compared to the data of AMS02 (Aguilar et al. 2021c) Bottom left panel: Al modulated flux (red solid line) and its secondary component (blue solid line) compared to the data of AMS02 (Aguilar et al. 2021c) Bottom right panel: S modulated flux (red solid line) and its secondary component (blue solid line) compared to the data of AMS02 (Aguilar et al. 2023). |
As a consistency check of our approach and of the considered production channels, in Fig. B.1 and Fig. B.2 we show our predictions for the Ar, Ca, Cl, Cr, K, Mn, P, Sc, Ti, and V fluxes. For these nuclei the data are mostly available at Ek ≲ 50 GeV/n, while higher energy data, if present, show large uncertainties (Maurin et al. 2023).
5. Conclusions
Motivated by the recent report by DAMPE of a spectral steepening in the proton and He spectra at ≈15 TV, and by the flattening in the B/C ratio at ≈1 TeV/n reported by AMS02, CALET, and DAMPE, we proposed a global framework for the interpretation of current CR data, from ∼GV up to multi-PV rigidity.
The first ingredient of our model, is the idea that the DAMPE break may reflect the maximum CR rigidity reached in the bulk of SNRs, while only a fraction of CR sources (e.g., peculiar SNRs, star clusters) are assumed to accelerate particles to multi-PV, in agreement with state-of-the-art models of CR acceleration and γ-ray observations. This is rather in disagreement with the standard paradigm of the origin of CRs, where SNRs as a population are thought to be able to accelerate particles up to the knee, and the DAMPE break is thought to reflect either the peculiarity of some local source or a change in the propagation regime.
The second pillar of our scenario is a new perspective on the role played by the GD in the propagation of CRs, in particular in the TV-PV range. In the standard scenario of Galactic CR transport, the GH is considered the diffusion region, and the time spent by CRs in the GD is supposed to be due to the repeated crossings induced by scattering in the GH. In this view, the GD is mostly considered as a thin target for spallation reactions, but it is a passive entity for CR transport. Instead, motivated by the possibility, previously discussed in the literature, that severe damping processes may significantly suppress turbulence at the resonant scale in the GD, we propose a model where particles in the region experience a very weak scattering along magnetic field lines, which mostly lie parallel to the GP. At the same time, large-scale turbulence is expected to induce a diffusive motion perpendicular to the average Galactic field (and to the GP), which is energy-independent (or depends very weakly on the particle energy).
The intriguing result of such a setup is that beyond ≈TV the CR spectrum is shaped by the energy-independent propagation in the GD rather than by the repeated crossings of the disk induced by the CR diffusion in the GH. This naturally results in a smooth progressive hardening of the spectra of (mostly) primary species (p, He, C, O, Ne, Mg, Si, Fe) above approximately hundreds of GV, in agreement with the data. Moreover, it clearly predicts a flattening of the spectra of (mostly) secondary species (Li, Be, B, F) and of quantities such as the B/C ratio at multi-TV, which can be tested by experiments.
Moreover, this diffusive motion in the GD perpendicular to the GP provides a minimum, energy-independent residence time (which translates into a minimum grammage), which corresponds to the residence time experienced by very high-energy CRs, for which scattering in the GH becomes ineffective (since the diffusive mean free path becomes larger than the halo size). Remarkably, while at energies below a few TeV the grammage produced in sources could in principle be at the level of such residual grammage (see however the caveats discussed in the Introduction) at multi-TeV energies or higher, the source contribution is likely subdominant, and the detection of a flat B/C would provide support to our results.
Interestingly, in order to fit CR data, we found an effective diffusion coefficient in the GD (perpendicular to the GP) on the order of ≈ 1028 cm2/s, which is close to the diffusion coefficient of ≈10 − 100 TeV leptons inferred from pulsar TeV halos, and is ∼100 times smaller that the diffusion coefficient in the GH at those energies. This, on the one hand, provides some observational support to our model, and on the other hand, clearly shows that the investigation of pulsar TeV halos provides a unique tool for studying the propagation of multi-TV CRs, for which information from quantities such as the B/C ratio is still lacking.
The third central ingredient of our approach is the fact that, while CRs in the GD move diffusively perpendicular to the GP, they are assumed to move rather quickly along the GP. This means that even high-energy particles that are little scattered in the GH may come from a region around us ≫h. This may have a substantial impact on keeping the CR anisotropy small since the number of contributing sources may remain relatively large even at PV rigidity.
We assume a typical rate of SNe explosion in the GD (radius 10 kpc) of νSNe = 1/30 yr, that ξPV ∼ 15% of them accelerate to PV and that the residence time in the GH is as in Eq. (14). If during this time particles travel along the GP a distance d ≈ 1 kpc (see Eq. (16) in Sect. 2), the average number of contributing sources is
which becomes ⟨NPV⟩≈40 for d = 2 kpc. Explaining the CR anisotropy is a crucial test for our approach, and we defer its investigation to a forthcoming paper.
Acknowledgments
S. R. acknowledged support from by Istituto Nazionale di Fisica Nucleare (INFN) and the Italian Space Agency (ASI) through the ASI INFN agreement No. 2018-28-HH.0, Addendum No. 2018-28-HH.2-2022, CUP F16C18000430005.
References
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2019, Phys. Rev. D, 100, 082002 [Google Scholar]
- Abeysekara, A. U., Albert, A., Alfaro, R., et al. 2017, Science, 358, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2011, Science, 332, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Akaike, Y., Asano, K., et al. 2020, Phys. Rev. Lett., 125, 251102 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Akaike, Y., Asano, K., et al. 2021, Phys. Rev. Lett., 126, 241101 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Akaike, Y., Asano, K., et al. 2022, Phys. Rev. Lett., 129, 101102 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Akaike, Y., Asano, K., et al. 2023, Phys. Rev. Lett., 130, 171002 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Alberti, G., Alpat, B., et al. 2013, Phys. Rev. Lett., 110, 141102 [CrossRef] [PubMed] [Google Scholar]
- Aguilar, M., Aisa, D., Alpat, B., et al. 2015, Phys. Rev. Lett., 114, 171103 [CrossRef] [PubMed] [Google Scholar]
- Aguilar, M., Ali Cavasonza, L., Alpat, B., et al. 2016, Phys. Rev. Lett., 117, 091103 [CrossRef] [PubMed] [Google Scholar]
- Aguilar, M., Ali Cavasonza, L., Ambrosi, G., et al. 2018, Phys. Rev. Lett., 120, 021101 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Cavasonza, L. A., Allen, M. S., et al. 2021a, Phys. Rev. Lett., 126, 041104 [CrossRef] [Google Scholar]
- Aguilar, M., Cavasonza, L. A., Allen, M. S., et al. 2021b, Phys. Rev. Lett., 126, 081102 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Cavasonza, L. A., Alpat, B., et al. 2021c, Phys. Rev. Lett., 127, 021101 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Ali Cavasonza, L., Ambrosi, G., et al. 2021d, Phys. Rep., 894, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Ali Cavasonza, L., Alpat, B., et al. 2023, Phys. Rev. Lett., 130, 211002 [NASA ADS] [CrossRef] [Google Scholar]
- Ahn, H. S., Allison, P., Bagliesi, M. G., et al. 2009, ApJ, 707, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Alemanno, F., An, Q., Azzarello, P., et al. 2021, Phys. Rev. Lett., 126 [CrossRef] [Google Scholar]
- Aloisio, R., & Blasi, P. 2013, JCAP, 2013, 001 [CrossRef] [Google Scholar]
- An, Q., Asfandiyarov, R., Azzarello, P., et al. 2019, Sci. Adv., 5, eaax3793 [NASA ADS] [CrossRef] [Google Scholar]
- Antoni, T., Apel, W. D., Badea, A. F., et al. 2005, Astropart. Phys., 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Arteaga-Velázquez, C. J., Rivera-Rangel, D., Apel, W. D., et al. 2017, Int. Cosmic Ray Conf., 301, 316 [CrossRef] [Google Scholar]
- Bell, A. R., Schure, K. M., Reville, B., & Giacinti, G. 2013, MNRAS, 431, 415 [Google Scholar]
- Berezinskii, V. S., Bulanov, S. V., Dogiel, V. A., & Ptuskin, V. S. 1990, Astrophysics of Cosmic Rays (Amsterdam: North-Holland) [Google Scholar]
- Blasi, P. 2013, A&ARv, 21, 70 [Google Scholar]
- Boudaud, M., Génolini, Y., Derome, L., et al. 2020, Phys. Rev. Res., 2, 023022 [CrossRef] [Google Scholar]
- Bresci, V., Amato, E., Blasi, P., & Morlino, G. 2019, MNRAS, 488, 2068 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., Marcowith, A., Amato, E., et al. 2020, Space Sci. Rev., 216, 42 [CrossRef] [Google Scholar]
- Casse, F., Lemoine, M., & Pelletier, G. 2001, Phys. Rev. D, 65, 023002 [NASA ADS] [CrossRef] [Google Scholar]
- Cerri, S. S., Gaggero, D., Vittino, A., Evoli, C., & Grasso, D. 2017, JCAP, 2017, 019 [Google Scholar]
- Chandran, B. D. G. 2000, ApJ, 529, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Chernyshov, D. O., Ivlev, A. V., & Dogiel, V. A. 2024, A&A, 686, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coste, B., Derome, L., Maurin, D., & Putze, A. 2012, A&A, 539, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowsik, R., & Burch, B. 2010, Phys. Rev. D, 82, 023009 [NASA ADS] [CrossRef] [Google Scholar]
- Cowsik, R., & Madziwa-Nussinov, T. 2016, ApJ, 827, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Cristofari, P. 2021, Universe, 7, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Cristofari, P., Blasi, P., & Amato, E. 2020, Astropart. Phys., 123, 102492 [Google Scholar]
- D’Angelo, M., Blasi, P., & Amato, E. 2016, Phys. Rev. D, 94, 083003 [CrossRef] [Google Scholar]
- Dampe Collaboration, 2022, Sci. Bull., 67, 2162 [CrossRef] [Google Scholar]
- Di Mauro, M., Korsmeier, M., & Cuoco, A. 2024, Phys. Rev. D, 109, 123003 [NASA ADS] [CrossRef] [Google Scholar]
- Dogiel, V. A., Schönfelder, V., & Strong, A. W. 2002, ApJ, 572, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Evoli, C., Blasi, P., Morlino, G., & Aloisio, R. 2018a, Phys. Rev. Lett., 121, 021102 [NASA ADS] [CrossRef] [Google Scholar]
- Evoli, C., Gaggero, D., Vittino, A., et al. 2018b, JCAP, 2018, 006 [Google Scholar]
- Evoli, C., Aloisio, R., & Blasi, P. 2019, Phys. Rev. D, 99, 103023 [CrossRef] [Google Scholar]
- Evoli, C., Morlino, G., Blasi, P., & Aloisio, R. 2020, Phys. Rev. D, 101, 023013 [NASA ADS] [CrossRef] [Google Scholar]
- Farmer, A. J., & Goldreich, P. 2004, ApJ, 604, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Fornieri, O., Gaggero, D., Cerri, S. S., De La Torre Luque, P., & Gabici, S. 2021a, MNRAS, 502, 5821 [NASA ADS] [CrossRef] [Google Scholar]
- Fornieri, O., Gaggero, D., Guberman, D., et al. 2021b, Phys. Rev. D, 104, 103013 [NASA ADS] [CrossRef] [Google Scholar]
- Gabici, S., Gaggero, D., & Zandanel, F. 2016, ArXiv e-prints [arXiv:1610.07638] [Google Scholar]
- Gabici, S., Evoli, C., Gaggero, D., et al. 2019, Int. J. Mod. Phys. D, 28, 1930022 [CrossRef] [Google Scholar]
- Génolini, Y., Serpico, P. D., Boudaud, M., et al. 2017, Phys. Rev. Lett., 119, 241101 [CrossRef] [Google Scholar]
- Génolini, Y., Maurin, D., Moskalenko, I. V., & Unger, M. 2018, Phys. Rev. C, 98, 034611 [CrossRef] [Google Scholar]
- Génolini, Y., Maurin, D., Moskalenko, I. V., & Unger, M. 2024, Phys. Rev. C, 109, 064914 [CrossRef] [Google Scholar]
- Gleeson, L. J., & Axford, W. I. 1968, ApJ, 154, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Grebenyuk, V., Karmanov, D., Kovalev, I., et al. 2019a, Adv. Space Res., 64, 2546 [NASA ADS] [CrossRef] [Google Scholar]
- Grebenyuk, V., Karmanov, D., Kovalev, I., et al. 2019b, Adv. Space Res., 64, 2559 [NASA ADS] [CrossRef] [Google Scholar]
- Hooper, D., Blasi, P., & Serpico, P. D. 2009, JCAP, 2009, 025 [CrossRef] [Google Scholar]
- Jacobs, H., Mertsch, P., & Phan, V. H. M. 2023, MNRAS, 526, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Jokipii, J. R., & Parker, E. N. 1969, ApJ, 155, 777 [Google Scholar]
- Kadomtsev, B. B., & Pogutse, O. P. 1979, Plasma Phys. Controlled Nucl. Fusion Res. 1978, 1, 649 [Google Scholar]
- Kamijima, S. F., & Ohira, Y. 2022, Phys. Rev. D, 106, 123025 [NASA ADS] [CrossRef] [Google Scholar]
- Karmanov, D. E., Kovalev, I. M., Kudryashov, I. A., et al. 2020, Sov. J. Exp. Theor. Phys. Lett., 111, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Kempski, P., Fielding, D. B., Quataert, E., et al. 2023, MNRAS, 525, 4985 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Duffy, P., & Gallant, Y. A. 1996, A&A, 314, 1010 [NASA ADS] [Google Scholar]
- Korsmeier, M., Donato, F., & Di Mauro, M. 2018, Phys. Rev. D, 97, 103019 [CrossRef] [Google Scholar]
- Lagutin, A. A., & Volkov, N. V. 2024, Phys. At. Nuclei, 86, 1069 [Google Scholar]
- Lazarian, A., & Xu, S. 2021, ApJ, 923, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., Xu, S., & Hu, Y. 2023, Front. Astron. Space Sci., 10 [Google Scholar]
- Lemoine, M. 2023, J. Plasma Phys., 89, 175890501 [CrossRef] [Google Scholar]
- Lipari, P. 2017, Phys. Rev. D, 95, 063009 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, Q., Qiao, B.-Q., Liu, W., Cui, S.-W., & Guo, Y.-Q. 2022, ApJ, 930, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, M. A., & Moskalenko, I. V. 2022, ApJ, 933, 78 [CrossRef] [Google Scholar]
- Malkov, M. A., Diamond, P. H., & Sagdeev, R. Z. 2012, Phys. Rev. Lett., 108, 081104 [NASA ADS] [CrossRef] [Google Scholar]
- Maurin, D. 2020, Comput. Phys. Commun., 247, 106942 [NASA ADS] [CrossRef] [Google Scholar]
- Maurin, D., Ahlers, M., Dembinski, H., et al. 2023, Eur. Phys. J. C, 83, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Mertsch, P. 2020, Ap&SS, 365, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Mertsch, P., Vittino, A., & Sarkar, S. 2021, Phys. Rev. D, 104, 103029 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzi, O., & Blasi, P. 2024, MNRAS, 529, L13 [Google Scholar]
- Porter, T. A., Jóhannesson, G., & Moskalenko, I. V. 2022, ApJS, 262, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Pshirkov, M. S., Tinyakov, P. G., Kronberg, P. P., & Newton-McGee, K. J. 2011, ApJ, 738, 192 [Google Scholar]
- Ptuskin, V. S., & Soutoul, A. 1998, Space Sci. Rev., 86, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Ptuskin, V., Zirakashvili, V., & Seo, E.-S. 2013, ApJ, 763, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Recchia, S., & Gabici, S. 2018, MNRAS, 474, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Recchia, S., Galli, D., Nava, L., et al. 2022, A&A, 660, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rechester, A. B., & Rosenbluth, M. N. 1978, Phys. Rev. Lett., 40, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A. 2020, Space Sci. Rev., 216, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A. 2021, Phys. Plasmas, 28, 120501 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 1971, ApJ, 170, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 1975, MNRAS, 172, 557 [CrossRef] [Google Scholar]
- Snodin, A. P., Jitsuk, T., Ruffolo, D., & Matthaeus, W. H. 2022, ApJ, 932, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Subedi, P., Sonsrettee, W., Blasi, P., et al. 2017, ApJ, 837, 140 [Google Scholar]
- Tatischeff, V., Raymond, J. C., Duprat, J., Gabici, S., & Recchia, S. 2021, MNRAS, 508, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Thoudam, S., & Hörandel, J. R. 2012, MNRAS, 421, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Tomassetti, N. 2012, ApJ, 752, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Tomassetti, N. 2015, Phys. Rev. D, 92, 081301 [NASA ADS] [CrossRef] [Google Scholar]
- Tomassetti, N., & Donato, F. 2012, A&A, 544, A16 [Google Scholar]
- Tripathi, R. K., Cucinotta, F. A., & Wilson, J. W. 1999, Universal Parameterization of Absorption Cross Sections, Technical Report, NASA/TP-1999-209726; NAS 1.60:209726; L-17832 [Google Scholar]
- Vieu, T., & Reville, B. 2023, MNRAS, 519, 136 [Google Scholar]
- Vink, J. 2012, A&ARv, 20, 49 [Google Scholar]
- Workman, R. L., Burkert, V. D., Crede, V., et al. 2022, Prog. Theor. Exp. Phys., 2022, 083C01 [CrossRef] [Google Scholar]
- Yoon, Y. S., Anderson, T., Barrau, A., et al. 2017, ApJ, 839, 5 [CrossRef] [Google Scholar]
- Zhao, M.-J., Fang, K., & Bi, X.-J. 2021, Phys. Rev. D, 104, 123001 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Advection and adiabatic losses
In this section we motivate the choice to neglect adiabatic losses in the transport equation, showing that for typical CR spectra, such term can be absorbed in the value of the advection velocity u required to fit CR data. To make the result more apparent we limit to the propagation of protons (so that we can neglect spallation) in the GH, with a rigidity dependent diffusion coefficient and a constant advection speed pointing away from the GP, namely du/dz = 2uδ(z).
We solve the transport equation for the distribution function f(p, z) (see, e.g., Evoli et al. 2019)
with the free-escape condition f(p, H) = 0
A.1. Solution for z ≠ 0
Equation (A.1) becomes
which, using the condition f(p, H) = 0 and f(p, 0)≡f0, gives
A.2. Integration around z = 0
Using the continuity of f0 across z = 0 and  we get
we get
The term
can be computed using Eq. (A.3) and plugged into Eq. (A.4) to get a differential equation for f0,
whose solution reads
Two important limits can be obtained in the advection-dominated regime, relevant at low momenta, and diffusion-dominated regime, relevant at high momenta:
where we assumed q0 ∝ p−γ and D ∝ p−δ. The quantity uH/D controls the transition between the two regimes, where at low p the steady-state spectrum resembles the injection spectrum and at high p it is steeper due to the momentum-dependent diffusion.
A.3. Approximate solution
In order to simplify the solution for f0, we rewrite Eq. (A.4) as
where  is minus the slope of f0 p3 divided by 3. Since generally CR spectra are close to perfect power laws ∝p−4 − α, with α ≈ 0 − 1, s0 is expected to vary quite slowly with p.
is minus the slope of f0 p3 divided by 3. Since generally CR spectra are close to perfect power laws ∝p−4 − α, with α ≈ 0 − 1, s0 is expected to vary quite slowly with p.
Assuming s0 to be constant we can solve Eq. (A.9) as
The advection-dominate and diffusion-dominated regimes read
which are the same of the general solution, if we consider that in the advection-dominated regime s0 ≈ γ/3 − 1.
We note that, posing s0 = 0 we get
This discussion shows that ignoring the adiabatic losses, or choosing a different spatial profile for u instead of  (for instance a smooth increase in the advection velocity from uadv(z = 0) = 0 to the value uadv(z > h) = u beyond the disk of size h), would slightly change, in the propagated spectrum, the momentum-dependent transition between the advective and diffusive regimes. To zero order, in fitting CR data, such effect can be absorbed in the best-fit value for the advection velocity. The same advection-dominated limit in Eq. (A.11) with a given u and s0 can be obtained setting s0 = 0 and u → u(1 + s0), namely with a slightly larger value of the advection velocity.
(for instance a smooth increase in the advection velocity from uadv(z = 0) = 0 to the value uadv(z > h) = u beyond the disk of size h), would slightly change, in the propagated spectrum, the momentum-dependent transition between the advective and diffusive regimes. To zero order, in fitting CR data, such effect can be absorbed in the best-fit value for the advection velocity. The same advection-dominated limit in Eq. (A.11) with a given u and s0 can be obtained setting s0 = 0 and u → u(1 + s0), namely with a slightly larger value of the advection velocity.
Appendix B: Analytic solution for stable nuclei
We start with Eq. (17), we neglect adiabatic losses (see Sect. A) and let τr → +∞ for stable nuclei. The transport equation becomes
where
are the injection from sources and the injection from spallation of heavier nuclei (per ISM atom), respectively, and H* = h + H as described in Sect. 3. We solve this equation with the assumptions of Eqs. (24, 25, 27), which we report here for completeness
The solution can be found similarly to the case presented in Sect. A.
B.1. Solution z ≠ 0
The transport equation reduces to
and in particular to
Using the solution of Eq. (A.3) for z > h we get
where Iαh is the particle flux at z = h.
Plugging the expression for 𝒦α into the equation for the GD we get
which can be integrated between z = 0+ and z = h−, taking into account the continuity in h, namely Iα, h+ = Iα, h− = Iαh
For the flux at z = 0, Iα0, we obtain
The latter expression can be rewritten in a more compact form by introducing
namely
B.2. Integration around z = 0
Using the fact that  we get
we get
Using Eq. (B.9) and Eq. (B.14) we can write
To bring the latter equation in the form of Eq. (28) we note that
where
as in Eq. (30).
We note that the term  was also found in Eq. (A.12) and can be interpreted as a modification of the diffusion coefficient in the GH, DH, that takes into account the advection (see also discussion in Sect. A). We introduce the effective diffusion coefficient
was also found in Eq. (A.12) and can be interpreted as a modification of the diffusion coefficient in the GH, DH, that takes into account the advection (see also discussion in Sect. A). We introduce the effective diffusion coefficient
The advection-dominated and diffusion-dominated regimes read
as expected in the two cases.
Finally, the expression for Iα0 becomes
as reported in Eq. (28).
 |
Fig. B.1. Fluxes of Ar, Ca, Cl, Cr, K, compared to a variety of data (taken from Maurin et al. 2023). |
 |
Fig. B.2. Fluxes of Mn, P, Sc, Ti, V, compared to a variety of data (taken from Maurin et al. 2023). |
Appendix C: Analytic solution for unstable nuclei
We follow the procedure used in Sect. B and solve the transport equation
where we introduced the radioactive decay rate νr(Ek) = 1/τr(Ek) = 1/τr0γ(Ek) (where τ0 is the decay time at rest and γ(Ek) the particle Lorentz factor) and removed the injection term from sources, since unstable nuclei are secondary.
As for the advection in the GH, in order to keep the analytic solution simpler, we treat it with the effective diffusion coefficient DHeff defined in Eq. (B.19), namely
We also impose the usual free-escape condition Iα(H*, Ek) = 0
C.1. Solution for z ≠ 0
Equation (C.1) reduces to
whose general solution reads
The constants ah, bh and bH as a function of aH are determined with the conditions
-
 (free escape)
(free escape) -
 (continuity in h)
(continuity in h) -
 (integration around h)
(integration around h) -

which gives
C.2. Integration around z = 0
We get
where  can be derived from Eq. (C.5). With some cumbersome algebra we can finally derive an expression for Iα0, namely
can be derived from Eq. (C.5). With some cumbersome algebra we can finally derive an expression for Iα0, namely
where we defined the quantities
It can be shown that  .
.
We note that  is a timescale ∝τhτr, where τh ≡ h2/Dh is the diffusion timescale in the GD.
is a timescale ∝τhτr, where τh ≡ h2/Dh is the diffusion timescale in the GD.
Similarly to the case of stable nuclei, we can introduce the grammage as in Eq. (31), and rewrite Eq. (C.7) as
C.3. Relevant limits
We conclude by analyzing simpler case of diffusion in the GH only (namely h → 0 and Dh → DH) and negligible spallation σα → 0. Under such assumptions, the solution can be simplified through
-
h → 0 ⟹ξh → 0
-
Dh → DH

which gives (we also multiply and divide by H)
Taking into account the diffusion timescale, τdiff(Ek)≡H2/DHeff(Ek), the following limits can be envisaged (see Berezinskii et al. 1990):
-
diffusion limit (relevant at high Ek)τdiff ≪ τr (ξH → 0; coth(ξH)→1/ξH) namely
which corresponds to the solution for secondary stable nuclei, Eq. (28) when spallation is neglected and h → 0;
-
decay limit (relevant at low Ek)τdiff ≫ τr (ξH → 1; coth(ξH)→1) namely
which can be interpreted as follows. In a time τr particles travel diffusively a distance
 , and thus experience an average density
, and thus experience an average density  instead of ndhd/H. Thus the equilibrium flux is given by
instead of ndhd/H. Thus the equilibrium flux is given bywhere the latter equality has been obtained by multiplying and dividing by H.
All Tables
All Figures
 |
Fig. 1. B/C (top panel), B/O (middle panel), and C/O (bottom panel) ratios compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2020, blue squares), and DAMPE (Dampe Collaboration 2022, cyan triangles). The solid red (dashed magenta) line corresponds to the ratio as a function of rigidity (kinetic energy per nucleon) and is compared to the AMS02 (CALET and DAMPE) data. The green (pink) shaded region corresponds to a 20% uncertainty in the secondary production cross section. The solid blue line corresponds to the B/C or B/O ratio when the B flux is multiplied by fB = 1.1, as in Fig. 7. |
| In the text | |
 |
Fig. 2. Antiprotons. Top left panel: Unmodulated (solid orange) and modulated (dashed red) p̄ flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots). The yellow (green) shaded region corresponds to a 10% (20%) uncertainty in the production cross section. Top right panel: p̄/p ratio compared to the data of AMS02 (Aguilar et al. 2021d, black dots). Bottom left panel: p̄ source term, computed as in Eq. (23) and corresponding to the flux reported in the top left panel of the present figure. Bottom right panel: Slopes of the p̄ source term (solid green line), of p̄ flux (blue solid line), and of the proton flux (red solid line) reported in Fig. 4. The solid cyan curve corresponds to the sum of the slope of |
| In the text | |
 |
Fig. 3. Schematic representation of the propagation setup. The size of the GD (violet region) is h ∼ 150 pc and the magnetic field lines are preferentially parallel to the GP. The CR transport perpendicular to the plane is dominated by the large-scale turbulence and is encompassed in the rigidity-independent diffusion coefficient Dh; the size of the GH (gray region) is H ∼ 4 kpc and the magnetic field lines are preferentially perpendicular to the GP. The CR transport perpendicular to the plane is dominated by resonant scattering on plasma waves, encompassed in the rigidity-dependent diffusion coefficient DH, plus the contribution of advection in a wind of velocity u. |
| In the text | |
 |
Fig. 4. Proton and helium fluxes in the range 1 − 105 TV. Top panel: Unmodulated (solid orange) and modulated (dashed red) proton flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2022, blue squares), CREAM (Yoon et al. 2017, magenta diamonds), and DAMPE (An et al. 2019, cyan triangles). Middle panel: Unmodulated (solid orange) and modulated (dashed red) He flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2023, blue squares), CREAM (Yoon et al. 2017, magenta diamonds), and DAMPE (Alemanno et al. 2021, cyan triangles). Bottom panel: p/He flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2023, blue squares), and NUCLEON (Karmanov et al. 2020, green points). |
| In the text | |
 |
Fig. 5. Cosmic-ray grammage as defined by Eq. (31). |
| In the text | |
 |
Fig. 6. Proton fluxes (left panel) and He fluxes (right panel) compared to the data of DAMPE (An et al. 2019; Alemanno et al. 2021, cyan triangles), NUCLEON (Grebenyuk et al. 2019a, green points), Icecube-Icetop (Aartsen et al. 2019, orange diamonds), KASCADE (Antoni et al. 2005, pink and violet points), and KASCADE-Grande (Arteaga-Velázquez et al. 2017, yellow points). The red curves correspond to the case with two source populations. The blue curves correspond to the case of a source CR luminosity decreasing with the increase in maximum rigidity. |
| In the text | |
 |
Fig. 7. LiBeB and CNO nuclei. Top left panel: C flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CALET (Adriani et al. 2020, blue squares), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). Center left panel: N flux compared to the data of AMS02 (Aguilar et al. 2021d, black dots), CREAM (Ahn et al. 2009, magenta diamonds). Bottom left panel: O flux compared to the data of AMS02 (Aguilar et al. 2021d, 2023, black dots and yellow diamonds), CALET (Adriani et al. 2020, blue squares), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). The solid red line corresponds to the total modulated flux, while the solid blue line to the (modulated) secondary contribution to the given nucleus. The cyan (blue) shaded region corresponds to a 10% (20%) uncertainty in the secondary production cross section, which translates in the yellow (green) shaded region in the total flux. Right panels: Li, Be, and B fluxes compared to the data of AMS02 (Aguilar et al. 2021d, black dots) and CALET (Adriani et al. 2020, blue squares). The solid red line corresponds to the total modulated flux. The yellow (green) shaded region corresponds to a 10% (20%) uncertainty in the secondary production cross section. The solid blue line corresponds to the total flux multiplied by fLi = 0.92 (Li), fBe = 0.9 (Be) and fB = 1.1 (B). |
| In the text | |
 |
Fig. 8. Be/C (top left panel), Be/O (top right panel), and Be/B (bottom left panel) ratios (red solid line) compared to the data of AMS02 (Aguilar et al. 2018, 2021d, black dots). The green shaded region corresponds to a 20% uncertainty in the secondary production cross section. The solid blue line corresponds to the Be/C, Be/O, or Be/B ratio when the Be flux is multiplied by fBe = 0.9 and the B flux by fB = 1.9, as in Fig. 7. The 10Be/9Be ratio (bottom right panel) is compared to the preliminary AMS02 data (black dots) and to the data of a variety of other experiments, collected from the Cosmic-Ray Database (Maurin et al. 2023). The solid red line corresponds to a GH size of H = 4 kpc. The yellow, green, and pink shaded regions corresponds to a 10%, 20%, and 30% uncertainty in the production cross section, respectively. The solid cyan and purple lines correspond to H = 6 kpc and H = 8 kpc, respectively. |
| In the text | |
 |
Fig. 9. Ne, Mg, Si, and Fe modulated fluxes (red solid line) and their secondary component (blue solid line). Top left panel: Ne flux compared to the data of AMS02 (Aguilar et al. 2021d, 2023, black dots, yellow diamonds), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). Top right panel: Mg modulated flux compared to the data of AMS02 (Aguilar et al. 2021d, 2023, black dots, yellow diamonds), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). The dashed green line is obtained by multiplying the secondary component by 2. Bottom left panel: Si flux compared to the data of AMS02 (Aguilar et al. 2021d, 2023, black dots, yellow diamonds), CREAM (Ahn et al. 2009, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). The dashed green line is obtained by multiplying the secondary component by 1.2. Bottom right panel: Fe flux compared to the data of AMS02 (Aguilar et al. 2021a, black dots), CALET (Adriani et al. 2021, magenta diamonds), and NUCLEON (Grebenyuk et al. 2019a, green triangles). |
| In the text | |
 |
Fig. 10. F, Na, Al, and S modulated fluxes. Top left panel: F modulated flux (red solid line) compared to the data of AMS02 (Aguilar et al. 2021b, 2023, blackdots, yellowdiamonds). Top right panel: Na modulated flux (red solid line) and its secondary component (blue solid line) compared to the data of AMS02 (Aguilar et al. 2021c) Bottom left panel: Al modulated flux (red solid line) and its secondary component (blue solid line) compared to the data of AMS02 (Aguilar et al. 2021c) Bottom right panel: S modulated flux (red solid line) and its secondary component (blue solid line) compared to the data of AMS02 (Aguilar et al. 2023). |
| In the text | |
 |
Fig. B.1. Fluxes of Ar, Ca, Cl, Cr, K, compared to a variety of data (taken from Maurin et al. 2023). |
| In the text | |
 |
Fig. B.2. Fluxes of Mn, P, Sc, Ti, V, compared to a variety of data (taken from Maurin et al. 2023). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.






















![$$ \begin{aligned}&-\frac{\partial }{\partial z} \left[D_{\alpha } \frac{\partial I_{\alpha }}{\partial z} - u I_{\alpha }\right] - \frac{d\,u}{d\,z} \frac{I_{\alpha }}{3} \frac{\partial \ln (I_{\alpha }\,p)}{\partial \ln p} =\end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq33.gif)



![$$ \begin{aligned} q^\mathrm{PeV}_{0\alpha } = \epsilon _{\rm bulk}^\mathrm{PeV}\left[ \frac{\epsilon _{\alpha } E_{SN} \mathcal{R} _{SN}}{\pi R_d^2\, \mathcal{G} (\gamma ) c(m_p c)^4} \left(\frac{p}{m_pc}\right)^{-\gamma } \right]e^{-R/R^\mathrm{PeV}_{\rm max}}; \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq42.gif)







![$$ \begin{aligned} I_{\alpha 0}(E_k) = \frac{\tau _{\alpha }^{hH}}{1 + n_d\,\frac{h_d}{h}\, v(E_k)\sigma _{\alpha }\tau _{\alpha }^{hH}} \times \left[\frac{1}{2h}\mathcal{Q} _{\alpha , \mathrm {src}} + n_d \frac{h_d}{h}\mathcal{Q} _{\alpha , \mathrm {spall}} \right]. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq58.gif)



![$$ \begin{aligned} I_{\alpha 0}(E_k) = \frac{1}{1 + \frac{X_{\alpha }(E_k)}{X_{\mathrm{cr} \alpha }}} \times \left[\frac{\tau _{\alpha }^{hH}}{2\,h}\mathcal{Q} _{\alpha , \mathrm {src}} + \frac{X_{\alpha }(E_k)}{\mu v(E_k)}\mathcal{Q} _{\alpha , \mathrm {spall}} \right] .\end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq63.gif)
![$$ \begin{aligned} I_{\alpha 0}(E_k) = \frac{\mathcal{Q} _{\alpha , \mathrm {src}}}{2} \left[\frac{h}{D_h} + \frac{H}{D_H} \frac{1-\exp ^{-\frac{u\,H}{D_H}}}{\frac{u\,H}{D_H}}\right], \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq64.gif)
![$$ \begin{aligned} R^{*} = \left[80 \frac{H}{4\, \mathrm {kpc}} \frac{h}{150\, {\mathrm {pc}}} \frac{D_m}{\mathrm{pc}} \frac{10^{28}\mathrm {cm}^2/\mathrm {s}}{D_0} \right]^{1/\delta }\, \mathrm {GV}. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq65.gif)



![$$ \begin{aligned} R_H^\mathrm{mfp} = \left[12\times 10^3 \frac{H}{4\, \mathrm {kpc}} \frac{10^{28}\mathrm {cm}^2/\mathrm {s}}{D_0} \right]^{1/\delta }\, \mathrm {GV}. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq69.gif)





![$$ \begin{aligned} - \frac{\partial }{\partial z} \left[D \frac{\partial f}{\partial z} - u f \right] -2\,u\,\delta (z) \frac{1}{3p^2} \frac{\partial (f\,p^3)}{\partial p} = q_0\,\delta (z), \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq87.gif)


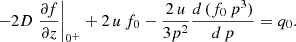


![$$ \begin{aligned} f_0(p) = \frac{3}{2\,u} \int _p^{\infty } \frac{d\,p^{\prime }}{p^{\prime }} q_0(p^{\prime })\exp \left[-3\int _p^{p^{\prime }} \frac{dp^{\prime \prime }}{p^{\prime \prime }} \frac{e^{-\frac{uH}{D(p^{\prime \prime })}}}{1-e^{-\frac{uH}{D(p^{\prime \prime })}}} \right]. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq94.gif)


![$$ \begin{aligned} f_0(p) = \frac{q_0\, H}{2\, D} \,\frac{1-e^{-\frac{uH}{D}}}{\frac{u\,H}{D} + s_0 \frac{u\,H}{D}\left[1-e^{-\frac{uH}{D}} \right]}. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq98.gif)

![$$ \begin{aligned} f_0(p) \rightarrow \frac{Q_0}{2} \left[\frac{H}{D} \frac{1-e^{-\frac{uH}{D}}}{\frac{u\,H}{D}}\right]. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq100.gif)
![$$ \begin{aligned} -\frac{\partial }{\partial z} \left[D_{\alpha } \frac{\partial I_{\alpha }}{\partial z} - u I_{\alpha }\right]&+ \, 2\,h_d\,n_d v(E_k)\sigma _{\alpha }(E_k)\delta (z) I_{\alpha } = \\ \nonumber&h \delta (z)\left[\frac{\mathcal{Q} _{\alpha , \mathrm {src}}}{h}\, +\, 2n_d\frac{h_d}{h} \mathcal{Q} _{\alpha , \mathrm {spall}}\right] \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq102.gif)









![$$ \begin{aligned} I_{\alpha 0} = I_{\alpha h} \left[1+\frac{u\,h}{D_h} \frac{1}{1-e^{-\frac{u\,H}{D_H}}}\right]. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq112.gif)

![$$ \begin{aligned} I_{\alpha 0} = I_{\alpha h} \left[1+\frac{\chi _h}{1-e^{-\chi _H}}\right]. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq114.gif)
![$$ \begin{aligned} -2\,\mathcal{K} _{\alpha } + 2\,h_d\,n_d v\sigma _{\alpha } I_{\alpha 0} = 2\,h \left[\frac{\mathcal{Q} _{\alpha , \mathrm {src}}}{2\,h}\, +\,n_d\frac{h_d}{h}\mathcal{Q} _{\alpha , \mathrm {spall}}\right]. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq116.gif)
![$$ \begin{aligned} I_{\alpha 0}(E_k) = \frac{ \left(\frac{\mathcal{Q} _{\alpha , \mathrm {src}}}{2\,h}\, +\,n_d\frac{h_d}{h}\mathcal{Q} _{\alpha , \mathrm {spall}}\right)\,h \left[ 1-e^{-\chi _H} + \chi _h\right] }{u + h_d\,n_d\, v\, \sigma _{\alpha }\, (1-e^{-\chi _H} + \chi _h)}. \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq117.gif)
![$$ \begin{aligned} h \left[ 1-e^{-\chi _H} + \chi _h\right]&= h \left[ \frac{1-e^{-\chi _H}}{\chi _H} \chi _H + \chi _h\right] \\ \nonumber&= u\, \tau _{\alpha }^{h\,H}, \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq118.gif)



![$$ \begin{aligned} I_{\alpha 0}(E_k) = \frac{\tau _{\alpha }^{hH}}{1 + n_d\,\frac{h_d}{h}\, v(E_k)\sigma _{\alpha }\tau _{\alpha }^{hH}} \times \left[\frac{\mathcal{Q} _{\alpha , \mathrm {src}}}{2h} + n_d\frac{h_d}{h} \mathcal{Q} _{\alpha , \mathrm {spall}} \right], \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq123.gif)
![$$ \begin{aligned} -\frac{\partial }{\partial z}&\left[D_{\alpha } \frac{\partial I_{\alpha }}{\partial z} \right] +\nu _r I_{\alpha } = \\ \nonumber&- \, 2\,h_d\,n_d v(E_k)\sigma _{\alpha }(E_k)\delta (z) I_{\alpha } + 2\,h\delta (z) \left[n_d\frac{h_d}{h} \mathcal{Q} _{\alpha , \mathrm {spall}}\right], \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq124.gif)



![$$ \begin{aligned} {\left\{ \begin{array}{ll} I_{\alpha }^\mathrm{GH}&= 2\,a_H \sinh \left(\xi _H \frac{H^* - z}{H}\right)\\ \\ I_{\alpha }^\mathrm{GD}&= 2\,a_H \sinh (\xi _H)\cosh \left(\xi _h \frac{h - z}{h}\right)\\&\; + 2\,a_H \frac{H}{h}\frac{\xi _h}{\xi _H} \cosh (\xi _H)\sinh \left(\xi _h \frac{h - z}{h}\right)\\ \\ I_{\alpha 0}&= 2\,a_H \left[\sinh (\xi _H)\cosh (\xi _h) + \frac{H}{h}\frac{\xi _h}{\xi _H} \cosh (\xi _H)\sinh (\xi _h) \right]. \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq132.gif)
![$$ \begin{aligned} -D_h \left.\frac{\partial I_{\alpha }^\mathrm{GD}}{\partial z} \right|_{0^+} + \,h_d\,n_d\, v\,\sigma _{\alpha } I_{\alpha 0} = h \left[n_d\frac{h_d}{h} \mathcal{Q} _{\alpha , \mathrm {spall}}\right], \end{aligned} $$](/articles/aa/full_html/2024/12/aa49005-23/aa49005-23-eq133.gif)






