EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A183 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A183
Number of page(s) 16
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/202346395
Published online 26 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Type Ia supernovae (SNe Ia), being high-luminosity standard-izable candles, have an essential importance in cosmic distance measurements, providing extension of the distance ladder toward higher redshifts. Since there is significant tension at present between the cosmological parameters, such as H0, inferred locally versus from the cosmic microwave background, it is important to further reduce the potential biases in the measured distances, as it may help reveal the cause of the discrepancy. Local galaxies that hosted SNe Ia and have observable Cepheid populations are especially important in this respect (Riess et al. 2022).

The basis of the standardization process of Type Ia light curves (LCs) is the Phillips relation (Phillips 1993), that is, the empirical correlation between the peak absolute brightness (typically in the B-band) and the Δm15 decline rate measured during the first 15 days after the moment of maximum light (t0). Multiple studies have tried to link the shape of the LC to the peak luminosity. The most widely used SN Ia LC synthesis and distance estimator codes are the newest versions of the Spectral Adaptive Light curve Template (SALT; Guy et al. 2005) and Multi-Color Light Curve Shape (MLCS; Riess et al. 1998; Jha et al. 2006), but other approaches, such as BayeSN (Thorp et al. 2021; Mandel et al. 2022) and SNooPy (Burns et al. 2011), have also been published (see Sect. 4.2).

Light curve fitters and distance estimations still suffer from intrinsic scattering due to spectrophotometric calibration issues and possibly some sort of unknown systematic effects. One way to reduce the sources of uncertainties is to use SN siblings, that is, SNe discovered in the same galaxy. These SNe have the same distance, redshift, and other physical properties as their common host galaxy. Therefore, the expected dispersion in their individually estimated distances should be significantly lower than the intrinsic scatter in the Hubble diagram at the same redshift. Thus, SN siblings may also allow us to test distance measurement methods and may support their further improvements (see e.g., Burns et al. 2020; Scolnic et al. 2020; Gallego-Cano et al. 2022; Hoogendam et al. 2022; Ward et al. 2022).

Because of the decade-long observations by recent transient discovery programs, the number of galaxies hosting multiple SNe is gradually increasing. The absolute record holder of modern times is NGC 6946, also called the Firework Galaxy, as it hosted ten SNe in a century. However, the datasets of early SNe usually suffer either from high uncertainties, data gaps, or a lack of wavelength coverage. Hence, not all SNe siblings can be used for high-precision distance estimations.

We searched for additional SN siblings in the Open Supernova Catalog (OSC; Guillochon et al. 2017). By narrowing our search to the simple Ia category in the OSC, we found 67 galaxies that hosted two or more “normal” Type Ia supernovae. The actual number is higher, as the OSC has a subclassification of Ia supernovae that we omitted from our search, and the catalog has not been updated since April 2021. Recent studies by Burns et al. (2020) and Gallego-Cano et al. (2022) have increased the sample further. In the most recent study by Kelsey (2023), 113 galaxies were found to host 236 thermonuclear SNe (including both “normal” SNe Ia and other subclasses) in the OSC.

There are only six galaxies in which at least three Type Ia SN siblings have been discovered. Both M84 (SNe 1957B, 1980I, and 1991bg) and NGC 1316 (SNe 1980N, 1981D, 2006dd, and 2006mr) include two Type Ia SNe before the charged-couple device (CCD) era, which increases the importance of NGC 5468 (SNe 1999cp, 2002cr, and 2005P), NGC 5018 (SNe 2017isq, 2002dj, 2021fxy), NGC 3367 (SNe 2018kp, 2003aa, 1986A), and NGC 3147 (SNe 1972A, 1997bq, 2008fv, and 2021hpr). The last galaxy hosted the recently discovered SN 2021hpr, which was the subject of intense follow-up observations by several observatories. Therefore, it became a key object in the distance estimations using Type Ia SN siblings.

In this paper, we present new optical photometric observations of SN 2021hpr and combine them with published LCs of SNe 1997bq and 2008fv to determine an improved distance to their common host galaxy, NGC 3147. Based on the improved distance, we infer and discuss the physical parameters for SN 2021hpr by building models for its spectra and the bolometric LC. The paper is structured as follows: In Sect. 2, we introduce the datasets of the three SNe Ia hosted by galaxy NGC 3147, with a special interest in the newly obtained LC of SN 2021hpr published in this paper first. Methods for the spectral synthesis and LC analysis, as well as the fitting algorithms used for distance estimations, are described in Sect. 4. The results are presented and discussed in Sect. 5. Finally, we summarize our conclusion in Sect. 6.

2 Three supernovae of NGC 3147

Located in the Draco constellation, NGC 3147 is a barred spiral galaxy at α(2000.0) = 10h16m50s, δ(2000.0) = +73°24′. It is of interest due to its low-luminosity Type II Seyfert active galactic nucleus (Panessa & Bassani 2002). Its heliocentric redshift is z = 0.00934 (Epinat et al. 2008). The historical distance estimations show a wide range between 27.7 Mpc (from Tully-Fisher relation; Bottinelli et al. 1984) and 55.2 Mpc (based on the Type Ia SN 1972A; Parodi et al. 2000), but the latest pre-SN 2021hpr results have narrowed it down to 39.3 Mpc (SN 1997bq; Tully et al. 2013) and 43.7 Mpc (SN 2008fv; Biscardi et al. 2012). The most recent Cepheid-based distance was derived by the comprehensive analysis of Riess et al. (2022), who estimated 40.1 Mpc ± 3.3 Mpc. Their analysis included 27 Cepheid variables of NGC 3147.

The proximity and face-on orientation of NGC 3147 makes it a prominent host for discovering transient events. In the past half-century, this galaxy hosted six SNe, four of which were classified as Type Ia (the other two, SN 2006gi and SN 2021do, were Type Ib/c events). For SN 1972H, only photographic photometry was published (Barbon et al. 1973). Thus, only SNe 1997bq, 2008fv, and the recently discovered 2021hpr can be used in a modern LC analysis.

The galactic component of the interstellar reddening in the direction of NGC 3147 is E(B – V) = 0.021 mag (Schlafly & Finkbeiner 2011). The explosions took place at distant sites within NGC 3147, sampling different regions of the galaxy and requiring different level of correction for interstellar reddening. The host galaxy component of the reddening was taken from previous studies for each object, as listed below.

Discovery of SN 1997bq was made on 50546.0 MJD by Laurie & Challis (1997). The SN was located outside the observable spiral arms of NGC 3147 with 60” offset (R ≈ 16.0 kpc) southeast from the bulge. The UBVRI LCs were obtained at the Fred Lawrence Whipple Observatory of the Harvard-Smithsonian Center for Astrophysics and published by Jha et al. (2006). Due to the outskirt location of SN 1997bq, no significant host galaxy reddening is expected, but the individual LC fit performed with the code Baye SN indicated a total extinction of AV = 0.45 mag (Ward et al. 2022).

On 54736.0 MJD, SN 2008fv was first detected by K. Ita-gaki to 37″ northeast from the bulge of NGC 3147 (Nakano et al. 2008). Biscardi et al. (2012) reported a significant host galaxy reddening of E(B – V)host = 0.22 with selective extinction coefficients of RV = 2.9 based on Cardelli et al. (1989). The SN peaked at 14.55 mag on ~54 749.0 MJD in the B-band. Optical and near-infrared (NIR) photometry was obtained by Tsvetkov & Elenin (2010) and Biscardi et al. (2012). However, there is an enormous difference between the two datasets in the I-band. The choice of the adopted magnitudes for the LC fitting is explained in Sect. 5.1.2.

The discovery of SN 2021hpr was reported by Itagaki (2021) based on a first observation on 59306.4 MJD. Later, a prediscovery detection (59304.92 MJD) was reported by Tsvetkov et al. (2021) by 0.3 day before the observation of the Zwicky Transient Factory. The first yet ambiguous classification (Tomasella et al. 2021) claimed that the new transient is probably a Type Ia SN due to its Si II λ6355 feature with an expansion velocity of 21 000 km s−1. The strong high-velocity feature and the rapid brightening of the object suggested that SN 2021hpr was discovered at its very early phase.

Two previous studies used SN 2021hpr as their subject, and they published and analyzed their independent follow-up observations. Zhang et al. (2022) presented BVRI LCs and optical spectra between −14 and +64 days to B-band maximum, while Ward et al. (2022) provided grizy photometry between −10 and +40 days and one optical spectrum at −4.2 days. In this study, we publish a new set of optical photometry obtained at two Hungarian observatories. Furthermore, we include the analysis of UV-photometry taken by the Neil Gehrels Swift Observatory Ultraviolet and Optical Telescope (UVOT). Hereafter, we use our new BV gri photometry, supplemented by Swift UBV data, for the LC analysis of SN 2021hpr. The previously published LCs mentioned above are also used for comparison but not for re-analysis. We also model the spectra of SN 2021hpr available in the literature (see Table A.4).

The host extinction was assumed to be negligible by Zhang et al. (2022), but the LC analysis of Ward et al. (2022) suggested AV,host ≃ 0.20 mag. Without any more established estimation, we use their mean value AV,host = 0.1 mag for the rest of the paper. The main properties of NGC 3147, as well as of the three SNe, are listed in Table 1.

3 Observations

In this paper, we present an SN photometric dataset that was obtained with two recently installed 0.8 m telescopes in Hungary: one at the Piszkéstető Mountain Station of the Konkoly Observatory and one at the Baja Observatory. The twin instruments are two 0.8 m Ritchy-Chrétien telescopes (hereafter KRC80 and BRC80, respectively) manufactured and deployed by the company Astro Systeme Austria (ASA). The focal length of 5700 mm provides an f/7 light-gathering power. The telescopes are equipped with Johnson BV and Sloan ugriz filters and a 2048 × 2048 back-illuminated FLI PL230 CCD chip with a pixel scale of 0.55″. Due to the similarities between the two telescopes, the combined LCs of SN 2021hpr can be considered as a homogeneous dataset.

We carried out standard Johnson–Cousins BV and Sloan griz CCD observations across 50 nights between April and September 2021 (Fig. 1). The achieved photometric accuracy varied between 0.01 and 0.05 mag depending on the weather conditions. The exposure times were 180 seconds, except for the B filters, where we used 300 sec.

All data were processed with standard IRAF1 routines, including bias, dark, and flat-field corrections. We co-added three images per filter per night aligned with the wcsxymatch, geomap and geotran tasks. We obtained point-spread function (PSF) photometry on the co-added frames using the daophot package in IRAF and image subtraction photometry based on other IRAF tasks such as psfmatch and linmatch, respectively. For the image subtraction, we applied a template image taken at a sufficiently late phase, that is, when the transient was no longer detectable on our frames.

For the PSF photometry, we built an automated pipeline using self-developed C-codes and bash shell scripts. The necessary IRAF tasks were referred to as system binaries outside the IRAF environment. The IRAF executables were collected into a single parallel processing script using gnu–parallel (Tange 2011). This “all-inclusive” method enabled us to reduce the processing time for the ~1 GB of data per night to a few minutes on a normal PC with 16 CPU cores.

The photometric calibration was carried out using stars from Data Release 1 of Pan-STARRS1 (PS1)2. The selection of the photometry reference stars and the calibration procedures are as follows. First, sources within a 5 arcmin radius around the SN with r-band brightness between 15 and 17 mag (to avoid saturation; Magnier et al. 2013) were downloaded from the PS1 catalog. Next, non-stellar sources were filtered out based on the criterion iPSFmag – iKronmag < 0.05 for stars.3 To obtain reference magnitudes for our Johnson B- and V-band frames, the PS1 magnitudes were transformed into the Johnson BVRI system based on equations and coefficients found in Tonry et al. (2012). Finally, the instrumental magnitudes were transformed into standard BV griz magnitudes by applying a linear color term (using g – i) and wavelength-dependent zero points. Since the reference stars fell within a few arcminutes around the target, no atmospheric extinction correction was necessary. We note that S -corrections were not applied.

The obtained BV griz LCs are plotted in Fig. 1. Direct comparison with B- and V-band LCs of Zhang et al. (2022) further confirmed that our data are free of systematic errors.

In the case of SN 2021hpr, the ground-based optical observations were supplemented by the available archival data of the Neil Gehrels Swift Observatory (Swift; Gehrels et al. 2004; Burrows et al. 2005) taken with UVOT (Roming et al. 2005) in April 2021 (see in Fig. 2). Data were collected in six filters from optical to ultraviolet wavelengths (u, b, υ, uυw1, uvm2, uvw2). The SN was detectable as a point source on the images, although it was located in a complex galactic environment. In order to model its background flux, we applied five different background regions distributed around the SN and determined the background as the average of the flux values taken from each region. The Swift UVOT data were processed using the HEA soft software package. We summed the individual frames using the uvotimsum task and carried out aperture photometry on the summed images using the uvotsource task.

Two spectra used in this study (see Table A.4) were published by Zhang et al. (2022), and another was obtained at Smolecin Observatory (L25). All spectra are available at the WISeREP online supernova database (Yaron & Gal-Yam 2012).

thumbnail Fig. 1

Comparison of BV griz photometry of SN 2021hpr from different data sources.
thumbnail Fig. 2

Swift photometry of SN 2021hpr.

4 Methods

4.1 The radiative transfer code TARDIS

Our approach for the fitting of the spectral series of SN 2021hpr was performed with the one-dimensional radiative transfer code TARDIS (Kerzendorf & Sim 2014). The TARDIS code calculates synthetic spectra on a wide wavelength range in exchange for a low computational cost, providing an ideal tool for fitting both the continuum and spectral features of homologously expanding ejecta.

The main assumption of the code is a sharp photosphere emitting blackbody radiation modeled via indivisible energy-packets representing bundles of photons (for further description see Abbott & Lucy 1985; Lucy & Abbott 1993; Lucy 1999, 2002, 2003). The model atmosphere is divided into radial layers with densities and chemical abundances defined by the user. The algorithm follows the propagation of the packets while calculating the wavelength- and direction-changing light-matter interactions based on a Monte Carlo scheme in every shell. The final output spectrum is built up by summarizing the photon packets escaping from the model atmosphere.

The approach of TARDIS offers several improvements from the simple local thermodynamic equilibrium (LTE) assumptions. We followed the same settings as in most of the studies that used TARDIS for spectral fitting (see e.g., Magee et al. 2016; Boyle et al. 2017; Barna et al. 2018). As an example, the ionization state of the material used here were estimated following an approximate non-LTE (NLTE) mode, the so-called nebular approximation, which significantly deviates from the LTE method by accounting for a fraction of recombinations returning directly to the ground state (Mazzali & Lucy 1993). The excitation state was calculated according to the dilute-LTE approximation, which is also not purely thermal. The summary of TARDIS numerical parameters and modes adopted in this study are listed in Table 2. The limitation of the simulation background, as well as the detailed description of the NLTE methods, are presented in the original TARDIS paper (Kerzendorf & Sim 2014).

Table 1

Main parameters of the three SNe Ia in NGC 3147.

Table 2

TARDIS fitting parameters.

4.2 Light curve fitter codes for SNe Ia

We applied the recently released version of SALT (i.e., SALT3; Kenworthy et al. 2021) for estimating the distance to SN 2021hpr and its two siblings. We also utilized the earlier version, SALT2.4 (Betoule et al. 2014), as well as an independent LC fitter, MLCS2k2 (Jha et al. 2007), to check the consistency of the inferred distance moduli with what was found in earlier calibrations.

The MLCS2k2 code is the improved version of the original MLCS code introduced by the High-z Supernova Search Team (Riess et al. 1996). The LCs obtained in Johnson-Cousins UBVRI filters were fitted with two tabulated functions (Pλ and Qλ) trained on a carefully selected sample of 133 SNe (Jha et al. 2007) and with the Δ parameter that linked the shape of the LC with the peak absolute brightness in the V-band. The code fits the observed LC mλ(t) with the following function: 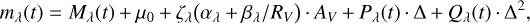mλ(t)=Mλ(t)+μ0+ζλ(αλ+βλ/RV)⋅AV+Pλ(t)⋅Δ+Qλ(t)⋅Δ2,${m_\lambda }\left( t \right) = {M_\lambda }\left( t \right) + {\mu _0} + {\zeta _\lambda }\left( {{\alpha _\lambda } + {{{\beta _\lambda }} \mathord{\left/ {\vphantom {{{\beta _\lambda }} {{R_V}}}} \right. \kern-\nulldelimiterspace} {{R_V}}}} \right) \cdot {A_V} + {P_\lambda }\left( t \right) \cdot {\rm{\Delta + }}{Q_\lambda }\left( t \right) \cdot {{\rm{\Delta }}^2},$(1)

where t is the rest-frame time (corrected for time dilation) elapsed from the moment of B-band maximum, Mλ(t) is the LC of the fiducial SN Ia in absolute magnitudes, and µ0 is the true (extinction-free) distance modulus. The MLCS2k2 code also takes into account the effect of interstellar reddening with AV extinction in the V-band. The interstellar reddening law as a function of wavelength is described by α, β, while ζ takes into account the temporal variation of the reddening correction due to the spectral evolution of the SN.

The SALT2 code was introduced by the Super Nova Legacy Survey Team (Guy et al. 2007). Unlike MLCS2k2, this code models the entire spectral energy distribution (SED) as a function of time. To do this, a combination of multiple color-dependent vectors is trained on a large sample of thoroughly chosen SNe. The components of the model function are F(λ,t)=x0⋅[ M0(λ,t)+x1⋅M1(λ,t) ]⋅exp(c⋅CL(λ)),$F\left( {\lambda ,t} \right) = {x_0} \cdot \left[ {{M_0}\left( {\lambda ,t} \right) + {x_1} \cdot {M_1}\left( {\lambda ,t} \right)} \right] \cdot \exp \left( {c \cdot {\rm{CL}}\left( \lambda \right)} \right),$(2)

where M0, M1, and CL are the trained vectors of SALT, while x0, x1, and c are fitting parameters representing the normalization, stretch and color of the SED, respectively.

The SALT3 code is a recent improvement to SALT2.4 developed by Kenworthy et al. (2021). It was trained on more than one thousand SN Ia spectra, making its sample an order of magnitude larger than the previous version of the code. The SALT3 code thus provides lower uncertainties and fewer systematics compared to the previous versions.

The SALT model does not contain the distance as a direct fitting parameter. Instead, it is inferred from the fitting parameters of the SALT3 code by the following formula (Tripp 1998): 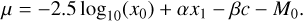μ=−2.5 log10 (x0)+αx1−βc−M0.$\mu = - 2.5\,{\log _{10}}\,\left( {{x_0}} \right) + \alpha {x_1} - \beta c - {M_0}.$(3)

We adopted the recent calibration of Pierel et al. (2022) for the α and β parameters. Thus, α = 0.133 ± 0.003 and β = 2.846 ± 0.017.

5 Results

5.1 Distance measurements

Recently, a comprehensive analysis of the distance of a multiple-SNe host galaxy was performed by Ward et al. (2022). The authors presented a new version of the Baye SN model (Thorp et al. 2021; Mandel et al. 2022) fitting the optical-NIR regime (in grizy bands) of SN 2021hpr but also included the photometry of SNe 1997bq and 2008fv, both individually and simultaneously. They inferred the mean value of the distance moduli as µ = 33.14mag with a standard deviation of 0.01, which is smaller than the intrinsic scattering of SNe Ia. The common µ-fit to the data of the three SNe resulted in µ = 33.13 ± 0.08 mag.

Ward et al. (2022) also compared Baye SN to the widely used LC-fitter code SNooPy. The SNooPy code provided a higher standard deviation of σ ~ 0.1 mag, but the mean value of the three individual distance moduli (µ = 33.18 mag) was close to that of the BayeSN code.

In the present paper, we apply SALT3 for an analysis similar to Ward et al. (2022) and use SALT2.4 and MLCS2k2 to cross-compare the inferred distance moduli. All LC fittings were computed separately on the individual datasets of SNe 1997, 2008fv, and 2021hpr. While SALT3 can be fed by a collection of various filters and magnitude systems, MLCS2k2 was trained for Johnson-Cousins UBVRI filters and Vega magnitudes. In the case of SN 2021hpr, where the object was not observed in Johnson-Cousins R and I filters, only B and V data were used during the fitting with MLCS2k2. The SALT3 fits are shown in Figs. 3–5, while MLCS2k2 and SALT2 fits can be seen in Figs. B.1–B.6.

Due to the low (z < 0.01) redshift of the host galaxy, K-correction for transforming observed LCs to rest-frame bands was estimated to be on the order of 0.01 mag, which is lower than the random observational uncertainties of the individual data. Thus, K-corrections were neglected. To avoid any discrepancy due to the different H0,ref values that were assumed to tie LC fitting codes to the distance scale, all distances were transformed to a common value of H0 = 73 km s−1 (Riess et al. 2022): 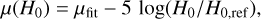μ(H0)=μfit−5  log(H0/H0,ref),$\mu \left( {{H_0}} \right) = {\mu _{{\rm{fit}}}} - 5\,\,\log \left( {{{{H_0}} \mathord{\left/ {\vphantom {{{H_0}} {{H_{0,{\rm{ref}}}}}}} \right. \kern-\nulldelimiterspace} {{H_{0,{\rm{ref}}}}}}} \right),$(4)

where µfit is the distance modulus inferred directly by the LC fitter. Despite the fact that all three LC-fitter codes have been trained for the U-band wavelengths, we refrained from using the U-band (both Johnson and Swift) magnitudes. The near-UV diversity of SNe Ia is not fully covered because of the limited sample of observations in the U-band. Thus, the training of the LC fitters would not be sufficient for this spectral regime and would increase the uncertainty of the distance estimation. The summary of the distance estimations of the three SNe inferred in this study can be found in Table 3.

thumbnail Fig. 3

SALT3 LC model fitting of the photometry of SN l997bq.
thumbnail Fig. 4

SALT3 LC model fitting of the photometry of SN 2008fv.
thumbnail Fig. 5

SALT3 LC model fitting of the photometry of SN 2021hpr.

5.1.1 SN 1997bq

The BVRI LCs of SN 1997bq are deficient around the peak, which makes constraining the date of maximum light more difficult. The polynomial fit of the B-band LC provided Tmax(B) = 50 557.5 MJD, which is consistent with the result of SALT when the time of maximum is a fitting parameter (Tmax(B) = 50 558.0 MJD). Adopting the latter date for the MLCS2k2, the inferred host galaxy extinction is Ahost = 0.60 mag, and the constrained distance modulus, µ = 33.00 mag, is close to the Cepheid-distance (µCeph = 33.014 ± 0.165 mag, Riess et al. 2022).

The SALT distances perfectly coincide with each other and also support our final conclusion about the distance of NGC 3145 (see below). Moreover, they are in between the previous estimates published by Tully et al. (2013) and (Jha et al. 2007; 32.97 and 33.16 mag, respectively, assuming H0 = 73 km s−1, see Eq. (4)) and are based on the same photometric data of SN 1997bq.

5.1.2 SN 2008fv

For SN 2008fv, the publicly available I-band observations of Biscardi et al. (2012) are significantly brighter than expected, and they exceed the published I-band magnitudes of Tsvetkov & Elenin (2010) by ~0.8 mag. Ward et al. (2022) investigated the colors of SN 2008fv and concluded that the I-band data of Biscardi et al. (2012) are probably inaccurate. Thus, they were discarded from the fitting process. The Biscardi et al. (2012) photometry in other filters was also discredited by Ward et al. (2022), but the estimated discrepancy is on the order of 0.1 mag. In this study, we aimed to use most of the available data; thus, we adopted the complete BVR photometry of Biscardi et al. (2012) together with post-maximum observations of Tsvetkov & Elenin (2010) in BVRI.

The MLCS2k2 code provides µ08fv = 32.97 mag, which is in good agreement with the Cepheid-based distance modulus of the host galaxy (Riess et al. 2022). The total AV is constrained as 0.96 mag, significantly higher than that estimated by Ward et al. (2022) with the Baye SN code. At the same time, the nearly identical models of SALT2.4 and SALT3 fail to fit the I-band fluxes, and they infer significantly higher distance moduli of µ ~ 33.33 ± 0.09 and µ ~ 33.35 ± 0.05 mag, respectively.

Table 3

Comparison of the distance moduli estimated with different LC-fitter codes for the three studied SNe of NGC 3147.

5.1.3 SN 2021hpr

Among the three SNe extending from −15 to +100 days in BVRI and griz bands, SN 2021hpr has the most densely covered LCs. However, the z-band LC suffers from higher uncertainties due to inferior sky conditions during the observations. Thus, it was omitted from the fitting.

The MLCS2k2 fit was made using only the BV LCs from the (B)RC80 observations to keep the homogeneity of the dataset and avoid any systematic errors. However, the result (µ = 32.85 mag) greatly differs from any other distance modulus of this study, which underlines the importance of having a photometric dataset covering a wide spectral range. At the same time, the SALT codes provide good fits to the LCs in all bands around the maximum light, resulting in similar distance moduli within a 1σ agreement. As a further validation, we also included the BVRI photometry of Zhang et al. (2022) in the homogeneous BV griz dataset for additional modeling with SALT3. The extra LCs and data points barely changed the parameters of the fits (Fig. B.7), including the inferred distance modulus of µ = 33.15 mag.

As a conclusion, we propose the distance modulus µ = 33.14 ± 0.05 mag of SN 2021hpr estimated by SALT3 for the distance of NGC 3147. This distance shows a good match with the mean value of (all) the distance moduli (including SNe 1997bq and 2008fv) estimated in this study (µ = 33.12 ± 0.10 mag) and also with that of Ward et al. (2022; µ = 33.14 ± 0.12mag). Moreover, the inferred distance is consistent with the result of the Cepheid-based distance (µ = 33.01 ± 0.165 mag; Riess et al. 2022). The summary of the distance estimation of NGC 3147 published in the literature and inferred in this study can be found in Fig. 6 and in Table 4.

5.2 The physical properties of SN 2021hpr

5.2.1 Rise time

To constrain the moment of the explosion of SN 2021hpr, we adopted the assumption of the expanding fireball model. According to this model, the emerging pre-maximum flux increases as a power-law function of time (Arnett 1982; Nugent et al. 2011): 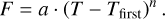F=a⋅(T−Tfirst)n.$F = a \cdot {\left( {T - {T_{{\rm{first}}}}} \right)^n}.$(5)

Here, Tfirst is the time of first light, which is not equivalent to the time of the explosion (Texp), as it refers to the moment when the first photons emerged, while the latter refers to the actual moment when the explosion started. The intermediate “dark phase” may last for a few hours or days (Piro & Nakar 2013; Firth et al. 2015).

In theory, the power-law function with n = 2 is valid only for the bolometric flux. However, studies have pointed out that it is still more-or-less valid for quasi-monochromatic fluxes in the optical bands, but in those cases, the value of the exponent may differ from the textbook example, varying between n = 2.2 (Ganeshalingam et al. 2011) and n = 2.44 (Firth et al. 2015) for normal SNe Ia.

We fit the early magnitudes of the most densely sampled LCs of SN 2021hpr (i.e., the B and V bands) simultaneously with Eq. (5) but using the same Tfirst for both LCs. At first, we fixed the exponent as n = 2, which corresponds to the classical fireball model. The resulting moment of first light is 59305.4 ± 1.5 MJD, which is slightly late in the aspect of the first detection a day later.

Next, we allowed n to vary between 2.0 and 2.5 for each LC (Fig. 7). The inferred date of Tfirst = 59304.6 ± 1.6 MJD is a more realistic time for the explosion, considering the early discovery 1.9 days later. The LC in the B-band peaked at 59 323.0 MJD, as it was constrained by polynomial fit. As a key parameter, this date was used as input for the MLCS2k2 and SALT2 fits in the followings. The estimated 18.4 day rise time is in good agreement with the average of normal SNe Ia (18.98 ± 0.54 days; Firth et al. 2015).

Table 4

Summary of the most recent distances estimated with various approaches.

thumbnail Fig. 6

Summary of the individual distance measurements involving the three SNe of NGC 3147. The MLCS2k2, SALT2, and SALT3 modeling is published in this study. The distance estimates conducted with BayeSN and SNooPy were published by Ward et al. (2022), while “Others” refers to the work of Jha et al. (2006), Biscardi et al. (2012), and Zhang et al. (2022). The most recent distance estimations based on Cepheid variables and cosmological redshift are also shown with horizontal lines.

5.2.2 Abundance tomography

We carried out modeling of the spectroscopic evolution of SN 2021hpr with the radiative transfer code TARDIS (Kerzendorf & Sim 2014). To synthesize the spectral luminosities, we fixed the distance of SN 2021hpr to 42.5 Mpc, corresponding the distance modulus carried out with SALT3 (see in Sect. 5.1.3). For de-reddening, a total of AV = 0.17 mag was adopted as the average value of the total extinction assumed by Zhang et al. (2022) and Ward et al. (2022).

Three of the earliest spectra of SN 2021hpr have been subjected to fitting (see in Table A.4). The best-fit synthetic spectra are presented in Fig. 8. The key parameters of the spectral synthesis are the total bolometric luminosity (L), the photospheric velocity (υphot), and the time since the explosion (texp, derived from Texp). We fixed the density function of our input to the well-known W7 model (Nomoto et al. 1984) to reduce the number of free parameters. We found that the latter simplification can result in a discrepancy if we assume the constrained Tfirst (see in Sect. 5.2.1) directly as Texp because the diluted density structure causes a too dense and too hot model ejecta, especially for the first epoch (59307.5 MJD). To compensate for this, we chose to fit Texp in our abundance tomography within the range of one day before Tfirst, taking into account an approximate dark phase. The best value is characterized as Texp = 59 304.0 MJD.

The spectral tomography taken at the earliest epoch samples the outermost layers, which is located above 18 000 km s−1 based on the υphot at texp = 3.5 days. Two other spectra were taken within half a day after the first epoch, but these data sets do not carry additional information, and thus, we did not include them in our analysis.

The next spectrum was taken at texp = 13.6 days, when the photosphere receded to 11 000 km s−1. This agrees with the conclusion of Zhang et al. (2022), where the authors classified SN 2021hpr as a high-velocity gradient (HVG; Benetti et al. 2005) SN Ia based on the ~800 km s−1 day−1 decrease of υphot.

Because of the exponentially decreasing density function toward higher velocities, the dominant light-matter interaction occurred in the few thousand kilometer-per-second-wide wide region above the photosphere (except for a few elements like Fe). Thus, the majority of the velocity domain over 10 800 km s−1 is poorly sampled.

Finally, a third epoch at texp = 19.9 days was chosen for spectral synthesis (υphot = 9800 km s−1). Assuming a linear decrease of υphot between the second and third epoch, we characterized υphot = 10 000 km s−1 at the moment of maximum light. After the maximum, the assumption of the black body emitting photosphere becomes weak in the case of the normal Type Ia SNe, which prevents the computation of realistic spectral fits with TARDIS.

To reduce the number of fitting parameters, we set the densities as fixed to the exponential fit of the W7 profile (see the upper panel of Fig. 9), adopting ρ0 = 4.7 g cm−3 as the central density at the reference time t0 = 100 s after the explosion and υ0 = 2750 km s−1 as the exponential decrease in the function: 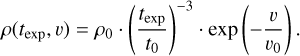ρ(texp,υ)=ρ0⋅ (texpt0)−3⋅exp (−υυ0).$\rho \left( {{t_{\exp }},\upsilon } \right) = {\rho _0} \cdot \,{\left( {{{{t_{\exp }}} \over {{t_0}}}} \right)^{ - 3}} \cdot \exp \,\left( { - {\upsilon \over {{\upsilon _0}}}} \right).$(6)

The summary of the input physical parameters producing the well-fitting synthetic spectra of Fig. 8 can be found in Table 5.

Despite the low time resolution, stratification of the chemical mass fractions can be mapped (Fig. 9), but the steep changes in the abundance functions cannot be tracked due to limited constraints. The first epoch samples the outermost region (υ > 18 200 km s−1), which was designed with the initial assumption of a pure C/O layer. The abundance of C is fit with a monotonously decreasing trend inward to the ejecta to reproduce the C II λ6580 line. The model of the outermost region also includes increased intermediate-mass element (IME) abundances in order to reproduce the high-velocity features observed at Ca II H&K, Si II, Ca II NIR lines frequently reported in the literature. Moreover, Mg is present in the model ejecta with a mass fraction of X(Mg) > 0.1, but here the only constraint is the tentative need for the Mg II λ4481, which if real is severely overlapped with features of ionized iron. The Fe II and Fe III features are very sensitive to the abundance at this early epoch, and we characterized it as X(Fe) = 0.01 above 18 200 km s−1. All these Fe and IME mass fractions are introduced on the conto of C/O abundances. We note that O is not a well-constrained element in our fitting process, as the O I λ7774 feature is relatively insensitive to the mass fraction of the element. Thus, we used X(O) as a filler in our chemical composition.

The majority of the model ejecta was designed according to the fit of the second spectral epoch (υphot = 10 900 km s−1); however, some compromises had to be implemented to achieve a better agreement for the third epoch, which showed only a slightly lower photospheric velocity (υphot = 9800 km s−1). The changes in the abundances of elements can be tracked by the absorption profile of the prominent lines. The red wing of the Ca II H&K profile caught by the second epoch constrains the inner abundances of the element with an upper limit of X(Ca) < 0.0005 below 16 000 km s−1. The Si and S abundances peak around ~ 13 000 km s−1 according to the fit of Si II λ6355 and S II W feature. The red wings of these absorptions also indicate reduced mass fractions toward the lower velocities.

The IGE elements (except the high-velocity Fe) are limited below ~ 14 000 km s−1; otherwise, the complex Fe feature around 5000 Å would be excessive at both epochs, especially toward the shorter wavelengths. Due to the limitations of IME abundances (see the paragraph above), Fe and Ni become the dominant elements here.

We note again that the derived abundance structure should be handled with caution due to the limited fitting constraints provided by the small spectral sample and the high number of fitting parameters. Between 9800 and 20 000 km s−1, the following three regions can be distinguished in the model ejecta by the general trend of the most prominent elements. A) C/O outer region: The chemical profile is dominated by O with an inward decreasing C contribution, while there is only a moderate IME and almost no IGE abundance. B) IME region: The mass fraction of Si is higher than 0.5 in a narrow 1000–2000 km s−1 wide region. The abundance of C/O drops, while the Ni abundance rises with decreasing velocity. C) IGE inner region: The 56Ni produced in the explosion and its daughter isotopes (56Co, 56Fe) dominate that ejecta.

This kind of stratification is not specific to only one explosion scenario. Instead, most of the deflagration-to-detonation transition and pure detonation models show similar regions with varying locations and relative strengths. The exact velocity boundaries, where these regions are separated from each other, just like the chemical abundances, are sensitive to the initial conditions of the hydrodynamic simulations. Thus, a direct quantitative comparison with predictions of any possible explosion scenario is not feasible from the present dataset.

thumbnail Fig. 7

Fit of BV LCs with the function 5 when allowing the exponent to vary between 2.0 < n < 2.5. A shared time of first light (Tfirst) was assumed for both LCs.
thumbnail Fig. 8

TARDIS fits (red lines) of the three spectral epochs (gray). The time since explosion (texp) is indicated in the upper-right corner.
Table 5

Summary of input parameters of the TARDIS model ejecta for each epoch of SN 2021hpr.

thumbnail Fig. 9

Inferred density (upper panel) and chemical abundances from the abundance tomography carried out via TARDIS fits of the three spectral epochs.

5.2.3 Analysis of the bolometric light curve

By using the distance modulus µ = 33.14 mag constrained in Sect. 5.1.3, physical properties such as the initial radioactive nickel mass produced in the explosion (MNi) can be constrained. To do so, we constructed the pseudo-bolometric LC of SN 2021hpr using two different methods. In both cases, we applied the available fluxes from the Swift UVM2 filter to the SDSS z-band but excluded the Swift UVW1 and UVW2 filters from the process because of their significant red leak (Brown et al. 2016). As a first approximation (hereafter referred to as BOL1), we used the SuperBol4 code for computing polynomial fits and extrapolations on the individual LCs. Then, before the integration, we extrapolated the observed SEDs with blackbody fits in the bluest and reddest bands for each epoch. By integrating these individual LCs, we generated the pseudo-bolometric LC with a BB-correction.

As a second method (BOL2), the flux contribution from the unobserved UV and IR regimes was estimated in another way. For integrating the UV contribution, the trapezoidal rule was applied with the assumption that the flux reaches zero at 1000 Å (Marion et al. 2014; Bora et al. 2022). The infrared contribution was taken into account by the exact integration of a Rayleigh-Jeans tail attached to the observed flux at the longest observed wavelength (i.e., I- or i-band in the present case). Hence, in the following sessions, we referred to this LC as the pseudo-bolometric LC with Rayleigh-Jeans tail.

There are multiple ways to estimate the initial 56Ni mass from the bolometric LC, for example, the t15 method (Sukhbold 2019) or the tail luminosity method (Afsariardchi et al. 2021). In this work, we fit the estimated pseudo-bolometric LC (supplemented with blackbody corrections) with a semi-analytic code based on the model of Arnett (1982) assuming radiative diffusion in a homologously expanding SN ejecta heated by the radioactive decay of 56Ni and 56Co. This model was developed further by Valenti et al. (2008) and Chatzopoulos et al. (2012).

The fitting parameters of the Arnett model are the mean diffusion timescale, td (also called the LC time scale, which is practically the geometric mean of the diffusion and the expansion timescales; see Arnett 1982); the gamma-ray leakage timescale, Tγ; and the initial mass of the radioactive 56Ni, MNi. These parameters are directly related to the global physical parameters of the ejecta, namely, the total ejecta mass Mej, the characteristic expansion velocity υexp, the effective optical opacity κ, and the opacity for gamma-rays κγ (see e.g., Könyves-Tóth et al. 2020).

Since the Arnett model provides only two timescales (td and Tγ) for three physical parameters (Mej, υexp, and κ), the physical parameters cannot be constrained independently from only photometry. To overcome this difficulty, Könyves-Tóth et al. (2020) used an approximate, iterative method by estimating a lower and an upper limit for the optical opacity first, then using the average of them to constrain the ejecta mass and the expansion velocity.

Recently, the diffusion model was challenged by Khatami & Kasen (2019), who suggested an alternative formalism to estimate the initial nickel masses for various types of SN explosions. However, Bora et al. (2022) demonstrated that for Type Ia SNe in particular, the nickel masses inferred from the two methods are consistent within their uncertainties.

As a first attempt, we fit the pseudo-bolometric LC (see in Fig. 10) provided by Super Bol (BOL1). The best-fit model parameters estimated by the Minim code (Chatzopoulos et al. 2013) are shown in Table 6 together with the inferred physical parameters. These data suggest a nickel mass of MNi ~ 0.48 M⊙, which is consistent with the absolute peak magnitude of Mmax(B) ~ 19 mag. However, the BOL1 LC suffers from higher uncertainties that are mainly due to the imperfect BB-extensions to the near-UV and near-IR regime fit by the Super Bol code. The strong bump between +20 and +30 days is partially nonphysical, as the BB-fits of the code overestimate the flux contribution from the not-observed spectral regimes. Since these uncertainties lead to an inferior fitting, we disfavor the results from the BOL1 LC.

The BOL2 LC was also fit (Fig. 10) following the same methodology, and the inferred physical quantities from the bestfit parameters (see Table 6) indicate a realistic MNi ~ 0.44 M⊙ and υexp ~ 11 200 km s−1. The mean optical opacity was constrained as κ ~ 0.144 according to the iterative method by Könyves-Tóth et al. (2020), which corresponds to an ejecta mass of ~1.12 M⊙.

As an alternative solution, the same set of best-fit parameters can be used with a fixed expansion velocity adopted from the spectral analysis (Sect. 5.2.2). The results are shown in the fourth column of Table 6. By assuming υphot = 10 000 km s−1 as vexp, we obtained a lower ejecta mass of Mej ~ 0.89 M⊙. We note, however, that even though υphot is generally used as an approximation for υexp, these two velocities are not the same quantity by definition (see Arnett 1982). Thus, this estimate can only be considered as a lower limit for the ejecta mass.

For further validation, we also constrained the value of the effective optical opacity (κ) by directly fitting the LC with the Arnett model-based LC2 code (Nagy & Vinkó 2016) coupled with Minim. In LC2 the ejecta mass, the radius of the progenitor, the nickel mass, the opacity, and the kinetic energy of the ejecta can be chosen as fitting parameters. Since our data span only the first few months after the explosion, we ignored the leaking of positrons from the ejecta and assumed only the usual gamma-ray leaking with an effective gamma-ray opacity of κγ ~ 0.03 cm2 g−1. The advantage of this approach is that the highly uncertain expansion velocity is not a fitting (nor an input) parameter. However, the results are sensitive to the value of κ included in the fitting. We note that due to significant param- eter correlations in the Arnett model (e.g., Nagy et al. 2014; Nagy & Vinkó 2016), all the previously described methods are tainted with significant systematic uncertainties. We took into account these correlations while estimating the average errors of the inferred physical properties of SN 2021hpr (see Table 6).

The main parameters inferred from the fitted κ method (Mej ~ 1.28 M⊙) are consistent with those estimated by the pre- vious approaches and are rather close to the results of the mean κ method. Thus, we accepted MNi = 0.44 ± 0.14 M⊙ and the other corresponding parameters as the final result of the bolometric LC analysis.

Table 6

Comparison of the physical parameters of SN 2021hpr from fitting the pseudo-bolometric LCs, taking into account gamma-ray leakage.

thumbnail Fig. 10

Pseudo-bolometric LCs estimated from the integration of observed magnitudes with trapezoidal approximation for the UV and Rayleigh-Jeans tail for the NIR contribution (red), and the LC estimated by blackbody fits to the UV/NIR regions (blue), and their best-fit Arnett-models (see Sect. 5.2.3).

6 Conclusion

We analyzed the optical/UV LC of the normal Type Ia SN 2021hpr together with its two well-observed siblings, SNe 1997bq and 2008fv, that appeared in the same host galaxy, NGC 3147. The three SNe provide a unique opportunity to revise the distance of their host and allow for the testing of systematic effects influencing various distance estimation methods.

We took new photometric data of SN 2021hpr with the twin robotic telescopes RC80 and BRC80 from two Hungarian observatories (Konkoly and Baja). The LCs, including BVgriz filters, start from t = −14.9 days, adopting 59 323.0 MJD as the moment of maximum light in the B-band. Based on the fitting of the early data points, we constrained Tfirst ~ 59 304.4 MJD as the date of first light, which gives trise = 18.4 days for the rise time. In addition to the optical follow-up, we also downloaded and analyzed the available Swift UVOT photometry taken from −16.1 to +12.3 days relative to the B-band maximum.

We estimated the distance to SN 2021hpr by fitting our new BVgri data with the LC-fitter codes MLCS2k2, SALT2, and SALT3. The same three codes were applied to the two sibling SNe, and the inferred individual distances were compared to each other. We found that the results scatter between µ = 32.97 and 33.35 mag, with a mean value of µ = 33.12 ± 0.16 mag. This estimation for the distance of NGC 3147 is in good agreement with previous SN-based studies (see Table 4 and Fig. 6) and also marginally consistent with the most recent Cepheid-based distance (µCeph = 33.01 ± 0.165 mag; Riess et al. 2022).

We adopted the distance inferred from the SALT3 fitting to SN 2021hpr, where the most complete self-consistent opti- cal dataset was applied and the models provided good fits to all bands. The SALT3-based distance modulus µ = 33.14 ± 0.05 mag is also consistent with that of Ward et al. (2022), esti- mated by the BayeSN code from fitting to an independent LC of SN 2021hpr.

To study the physical parameters of SN 2021hpr based on our new, improved distance, abundance tomography was per- formed by fitting three pre-maximum spectra with the radiative transfer code TARDIS. The constrained chemical structure is con- sistent with multiple explosion models, including deflagration-to-detonation transition and pure detonation scenarios, with an additional overabundance of Mg, Si, and Ca to reproduce the observed blue-shifts and high-velocity features of the corre- sponding absorption lines.

We calculated the bolometric LC of SN 2021hpr from its optical data supplemented by near-UV data from Swift and fit it with the radiative diffusion Arnett model. The peak lumi- nosity turned out to be 1.02 × 1043 erg/s, while the total mass of 56Ni produced in the explosion was estimated as 0. 44 ± 0.14 M⊙ and the ejecta mass and expansion velocity were calculated as 1.12 ± 0.28 M⊙ and 11200 ± 1200 km s−1, respec- tively. Considering all the estimated physical properties and spectroscopic characteristics of SN 2021hpr, we conclude that it belongs to the Branch-normal and high-velocity gradient classes of Type Ia SNe.

Acknowledgements

This research made use of TARDIS, a community-developed software package for spectral synthesis in supernovae (Kerzendorf & Sim 2014; Kerzendorf et al. 2023). The development of TARDIS received support from GitHub, the Google Summer of Code initiative, and from ESA’s Summer of Code in Space program. TARDIS is a fiscally sponsored project of NumFOCUS. TARDIS makes extensive use of Astropy and Pyne. The authors acknowledge the Hungarian National Research, Development and Innovation Office grants OTKA K-131508, K-138962, K-142534, FK-134432, KKP-143986 (Élvonal), and 2019-2.1.11-TéT-2019-00056. L.K. acknowledges the Hungarian National Research, Development and Innovation Office grant OTKA PD-134784. B.B., R.K.T. and Zs.B. are supported by the ÚNKP-22-2 New National Excellence Program of the Ministry for Culture and Innovation from the source of the National Research, Development and Innovation Fund. A.P.N. is supported by NKFIH/OTKA PD-134434 grant, which is founded by the Hungarian National Development and Innovation Fund. L.K., K.V., and T.S. are Bolyai János Research Fellows of the Hungarian Academy of Sciences. K.V. and T.S. are supported by the Bolyai+ grants ÚNKP-22-5-ELTE-1093 and ÚNKP-22-5-SZTE-591, respectively. S.Z. is supported by the National Talent Programme under NTP-NFTÖ-22-B-0166 Grant. Z.M.S. acknowledges funding from a St Leonards scholarship from the University of St Andrews. Z.M.S. is a member of the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne.

Appendix A Observational data

Table A.1

Log of SN 2021hpr photometry from the observatory of Baja.

Table A.2

Log of SN 2021hpr photometry from the observatory of Piszkesteto.

Table A.3

Log of Swift UVOT photometry of SN 2021hpr.

Table A.4

Log of the spectra. The time since the date of explosion constrained in the abundance tomography (MJD 59 304.0) is shown by texp, while the phases are given relative to the maximum in the B-band (MJD 59 321.9).

Appendix B Light curve fits

In this section, the plots of the MLCS2k2, SALT2.4, and SALT3 fits for SNe 1997bq, 2008fv, and 2021hpr are listed. The distance moduli estimated from these fits are discussed in Sect. 5.1, while the corresponding fitting parameters are listed in Table B.

Table B.1

Log of the LC fits.

thumbnail Fig. B.1

MLCS2k2 LC model fitting of the photometry of SN l997bq.
thumbnail Fig. B.2

SALT2.4 LC model fitting of the photometry of SN l997bq.
thumbnail Fig. B.3

MLCS2k2 LC model fitting of the photometry of SN 2008fv.
thumbnail Fig. B.4

SALT2.4 LC model fitting of the photometry of SN 2008fv.
thumbnail Fig. B.5

MLCS2k2 LC model fitting of the photometry of SN 2021hpr.
thumbnail Fig. B.6

SALT2.4 LC model fitting of the photometry of SN 2021hpr.
thumbnail Fig. B.7

SALT3 LC model fitting of the extended photometric dataset of SN 2021hpr.

References

  1. Abbott, D. C., & Lucy, L. B. 1985, ApJ, 288, 679 [NASA ADS] [CrossRef] [Google Scholar]
  2. Afsariardchi, N., Drout, M. R., Khatami, D. K., et al. 2021, ApJ, 918, 89 [NASA ADS] [CrossRef] [Google Scholar]
  3. Arnett, W. D. 1982, ApJ, 253, 785 [Google Scholar]
  4. Barbon, R., Ciatti, F., & Rosino, L. 1973, A & A, 29, 57 [NASA ADS] [Google Scholar]
  5. Barna, B., Szalai, T., Kerzendorf, W. E., et al. 2018, MNRAS, 480, 3609 [NASA ADS] [CrossRef] [Google Scholar]
  6. Benetti, S., Cappellaro, E., Mazzali, P. A., et al. 2005, ApJ, 623, 1011 [NASA ADS] [CrossRef] [Google Scholar]
  7. Betoule, M., Kessler, R., Guy, J., et al. 2014, A & A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Biscardi, I., Brocato, E., Arkharov, A., et al. 2012, A & A, 537, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bora, Z., Vinkó, J., & Könyves-Tóth, R. 2022, PASP, 134, 054201 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bottinelli, L., Gouguenheim, L., Paturel, G., & de Vaucouleurs, G. 1984, A & AS, 56, 381 [NASA ADS] [Google Scholar]
  11. Boyle, A., Sim, S. A., Hachinger, S., & Kerzendorf, W. 2017, A & A, 599, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Brown, P. J., Breeveld, A., Roming, P. W. A., & Siegel, M. 2016, AJ, 152, 102 [NASA ADS] [CrossRef] [Google Scholar]
  13. Burns, C. R., Stritzinger, M., Phillips, M. M., et al. 2011, AJ, 141, 19 [Google Scholar]
  14. Burns, C. R., Ashall, C., Contreras, C., et al. 2020, ApJ, 895, 118 [NASA ADS] [CrossRef] [Google Scholar]
  15. Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [Google Scholar]
  16. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
  17. Chatzopoulos, E., Wheeler, J. C., & Vinko, J. 2012, ApJ, 746, 121 [Google Scholar]
  18. Chatzopoulos, E., Wheeler, J. C., Vinko, J., Horvath, Z. L., & Nagy, A. 2013, ApJ, 773, 76 [NASA ADS] [CrossRef] [Google Scholar]
  19. Epinat, B., Amram, P., Marcelin, M., et al. 2008, MNRAS, 388, 500 [Google Scholar]
  20. Firth, R. E., Sullivan, M., Gal-Yam, A., et al. 2015, MNRAS, 446, 3895 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gallego-Cano, E., Izzo, L., Dominguez-Tagle, C., et al. 2022, A & A, 666, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Ganeshalingam, M., Li, W., & Filippenko, A. V. 2011, MNRAS, 416, 2607 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [Google Scholar]
  24. Guillochon, J., Parrent, J., Kelley, L. Z., & Margutti, R. 2017, ApJ, 835, 64 [Google Scholar]
  25. Guy, J., Astier, P., Nobili, S., Regnault, N., & Pain, R. 2005, A & A, 443, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Guy, J., Astier, P., Baumont, S., et al. 2007, A & A, 466, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Hoogendam, W. B., Ashall, C., Galbany, L., et al. 2022, ApJ, 928, 103 [NASA ADS] [CrossRef] [Google Scholar]
  28. Itagaki, K. 2021, Transient Name Server Discovery Report, 2021-998, 1 [Google Scholar]
  29. Jha, S., Kirshner, R. P., Challis, P., et al. 2006, AJ, 131, 527 [Google Scholar]
  30. Jha, S., Riess, A. G., & Kirshner, R. P. 2007, ApJ, 659, 122 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kelsey, L. 2023, MNRAS, submitted, [arXiv:2303.02020] [Google Scholar]
  32. Kenworthy, W. D., Jones, D. O., Dai, M., et al. 2021, ApJ, 923, 265 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kerzendorf, W. E., & Sim, S. A. 2014, MNRAS, 440, 387 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kerzendorf, W., Sim, S., Vogl, C., et al. 2023, tardis-sn/tardis: TARDISv2023.04.23 [Google Scholar]
  35. Khatami, D. K., & Kasen, D. N. 2019, ApJ, 878, 56 [NASA ADS] [CrossRef] [Google Scholar]
  36. Könyves-Tóth, R., Vinkó, J., Ordasi, A., et al. 2020, ApJ, 892, 121 [CrossRef] [Google Scholar]
  37. Laurie, S., & Challis, P. 1997, IAU Circ., 6616, 1 [NASA ADS] [Google Scholar]
  38. Lucy, L. B. 1999, A & A, 345, 211 [NASA ADS] [Google Scholar]
  39. Lucy, L. B. 2002, A & A, 384, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Lucy, L. B. 2003, A & A, 403, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Lucy, L. B., & Abbott, D. C. 1993, ApJ, 405, 738 [Google Scholar]
  42. Magee, M. R., Kotak, R., Sim, S. A., et al. 2016, A & A, 589, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Magnier, E. A., Schlafly, E., Finkbeiner, D., et al. 2013, ApJS, 205, 20 [Google Scholar]
  44. Mandel, K. S., Thorp, S., Narayan, G., Friedman, A. S., & Avelino, A. 2022, MNRAS, 510, 3939 [NASA ADS] [CrossRef] [Google Scholar]
  45. Marion, G. H., Vinko, J., Kirshner, R. P., et al. 2014, ApJ, 781, 69 [NASA ADS] [CrossRef] [Google Scholar]
  46. Mazzali, P. A., & Lucy, L. B. 1993, A & A, 279, 447 [NASA ADS] [Google Scholar]
  47. Mould, J. R., Huchra, J. P., Freedman, W. L., et al. 2000, ApJ, 529, 786 [Google Scholar]
  48. Nagy, A. P., & Vinkó, J. 2016, A & A, 589, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Nagy, A. P., Ordasi, A., Vinkó, J., & Wheeler, J. C. 2014, A & A, 571, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Nakano, S., Jacques, C., & Pimentel, E. 2008, Central Bureau Electronic Telegrams, 1520, 1 [NASA ADS] [Google Scholar]
  51. Nomoto, K., Thielemann, F. K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
  52. Nugent, P. E., Sullivan, M., Cenko, S. B., et al. 2011, Nature, 480, 344 [NASA ADS] [CrossRef] [Google Scholar]
  53. Panessa, F., & Bassani, L. 2002, A & A, 394, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Parodi, B. R., Saha, A., Sandage, A., & Tammann, G. A. 2000, ApJ, 540, 634 [NASA ADS] [CrossRef] [Google Scholar]
  55. Phillips, M. M. 1993, ApJ, 413, L105 [Google Scholar]
  56. Pierel, J. D. R., Jones, D. O., Kenworthy, W. D., et al. 2022, ApJ, 939, 11 [NASA ADS] [CrossRef] [Google Scholar]
  57. Piro, A. L., & Nakar, E. 2013, ApJ, 769, 67 [NASA ADS] [CrossRef] [Google Scholar]
  58. Riess, A. G., Press, W. H., & Kirshner, R. P. 1996, ApJ, 473, 88 [Google Scholar]
  59. Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [Google Scholar]
  60. Riess, A. G., Yuan, W., Macri, L. M., et al. 2022, ApJ, 934, L7 [NASA ADS] [CrossRef] [Google Scholar]
  61. Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [Google Scholar]
  62. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  63. Scolnic, D., Smith, M., Massiah, A., et al. 2020, ApJ, 896, L13 [NASA ADS] [CrossRef] [Google Scholar]
  64. Sukhbold, T. 2019, ApJ, 874, 62 [NASA ADS] [CrossRef] [Google Scholar]
  65. Tange, O. 2011, login: The USENIX Magazine, 36, 42 [Google Scholar]
  66. Thorp, S., Mandel, K. S., Jones, D. O., Ward, S. M., & Narayan, G. 2021, MNRAS, 508, 4310 [NASA ADS] [CrossRef] [Google Scholar]
  67. Tomasella, L., Benetti, S., Cappellaro, E., & Pastorello, A. 2021, Transient Name Server Classification Report, 2021-1031, 1 [Google Scholar]
  68. Tonry, J. L., Stubbs, C. W., Kilic, M., et al. 2012, ApJ, 745, 42 [Google Scholar]
  69. Tripp, R. 1998, A & A, 331, 815 [NASA ADS] [Google Scholar]
  70. Tsvetkov, D. Y., & Elenin, L. 2010, Peremennye Zvezdy, 30, 2 [NASA ADS] [Google Scholar]
  71. Tsvetkov, D. Y., Pavlyuk, N. N., Ikonnikova, N. P., Burlak, M. A., & Belinski, A. A. 2021, ATel, 14541, 1 [NASA ADS] [Google Scholar]
  72. Tully, R. B., & Fisher, J. R. 1988, Catalog of Nearby Galaxies [Google Scholar]
  73. Tully, R. B., Courtois, H. M., Dolphin, A. E., et al. 2013, AJ, 146, 86 [NASA ADS] [CrossRef] [Google Scholar]
  74. Valenti, S., Benetti, S., Cappellaro, E., et al. 2008, MNRAS, 383, 1485 [Google Scholar]
  75. Ward, S. M., Thorp, S., Mandel, K. S., et al. 2022, MNRAS, submitted, [arXiv:2209.10558] [Google Scholar]
  76. Yaron, O., & Gal-Yam, A. 2012, PASP, 124, 668 [Google Scholar]
  77. Zhang, Y., Zhang, T., Danzengluobu, et al. 2022, PASP, 134, 074201 [NASA ADS] [CrossRef] [Google Scholar]
1

IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.

All Tables

Table 1

Main parameters of the three SNe Ia in NGC 3147.

In the text
Table 2

TARDIS fitting parameters.

In the text
Table 3

Comparison of the distance moduli estimated with different LC-fitter codes for the three studied SNe of NGC 3147.

In the text
Table 4

Summary of the most recent distances estimated with various approaches.

In the text
Table 5

Summary of input parameters of the TARDIS model ejecta for each epoch of SN 2021hpr.

In the text
Table 6

Comparison of the physical parameters of SN 2021hpr from fitting the pseudo-bolometric LCs, taking into account gamma-ray leakage.

In the text
Table A.1

Log of SN 2021hpr photometry from the observatory of Baja.

In the text
Table A.2

Log of SN 2021hpr photometry from the observatory of Piszkesteto.

In the text
Table A.3

Log of Swift UVOT photometry of SN 2021hpr.

In the text
Table A.4

Log of the spectra. The time since the date of explosion constrained in the abundance tomography (MJD 59 304.0) is shown by texp, while the phases are given relative to the maximum in the B-band (MJD 59 321.9).

In the text
Table B.1

Log of the LC fits.

In the text

All Figures

thumbnail Fig. 1

Comparison of BV griz photometry of SN 2021hpr from different data sources.
In the text
thumbnail Fig. 2

Swift photometry of SN 2021hpr.
In the text
thumbnail Fig. 3

SALT3 LC model fitting of the photometry of SN l997bq.
In the text
thumbnail Fig. 4

SALT3 LC model fitting of the photometry of SN 2008fv.
In the text
thumbnail Fig. 5

SALT3 LC model fitting of the photometry of SN 2021hpr.
In the text
thumbnail Fig. 6

Summary of the individual distance measurements involving the three SNe of NGC 3147. The MLCS2k2, SALT2, and SALT3 modeling is published in this study. The distance estimates conducted with BayeSN and SNooPy were published by Ward et al. (2022), while “Others” refers to the work of Jha et al. (2006), Biscardi et al. (2012), and Zhang et al. (2022). The most recent distance estimations based on Cepheid variables and cosmological redshift are also shown with horizontal lines.
In the text
thumbnail Fig. 7

Fit of BV LCs with the function 5 when allowing the exponent to vary between 2.0 < n < 2.5. A shared time of first light (Tfirst) was assumed for both LCs.
In the text
thumbnail Fig. 8

TARDIS fits (red lines) of the three spectral epochs (gray). The time since explosion (texp) is indicated in the upper-right corner.
In the text
thumbnail Fig. 9

Inferred density (upper panel) and chemical abundances from the abundance tomography carried out via TARDIS fits of the three spectral epochs.
In the text
thumbnail Fig. 10

Pseudo-bolometric LCs estimated from the integration of observed magnitudes with trapezoidal approximation for the UV and Rayleigh-Jeans tail for the NIR contribution (red), and the LC estimated by blackbody fits to the UV/NIR regions (blue), and their best-fit Arnett-models (see Sect. 5.2.3).
In the text
thumbnail Fig. B.1

MLCS2k2 LC model fitting of the photometry of SN l997bq.
In the text
thumbnail Fig. B.2

SALT2.4 LC model fitting of the photometry of SN l997bq.
In the text
thumbnail Fig. B.3

MLCS2k2 LC model fitting of the photometry of SN 2008fv.
In the text
thumbnail Fig. B.4

SALT2.4 LC model fitting of the photometry of SN 2008fv.
In the text
thumbnail Fig. B.5

MLCS2k2 LC model fitting of the photometry of SN 2021hpr.
In the text
thumbnail Fig. B.6

SALT2.4 LC model fitting of the photometry of SN 2021hpr.
In the text
thumbnail Fig. B.7

SALT3 LC model fitting of the extended photometric dataset of SN 2021hpr.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.