| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201526288 | |
| Published online | 05 August 2015 | |
Warm and optically thick dissipative coronae above accretion disks
1
Copernicus Astronomical Center, Bartycka 18,
00-716
Warsaw,
Poland
e-mail:
agata@camk.edu.pl
2
Université de Toulouse, UPS-OMP, IRAP, 31000
Toulouse,
France
3
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
4
Center for Theoretical Physics, Al. Lotników 32/46,
02-680
Warsaw,
Poland
5
Université de Grenoble Alpes, IPAG, 38000
Grenoble,
France
6
CNRS, IPAG, 38000
Grenoble,
France
Received: 9 April 2015
Accepted: 9 June 2015
Context. In past years, several observations of AGN and X-ray binaries suggested the existence of a warm (T ~ 0.5 − 1 keV) and optically thick (τcor ~ 10 − 20) corona covering the inner parts of the accretion disk. These properties are directly derived from spectral fitting in UV to soft-X-rays using Comptonization models. However, whether such a medium can be both in radiative and hydrostatic equilibrium with an accretion disk is still uncertain.
Aims. We investigate the properties of such warm, optically thick coronae and put constraints on their existence.
Methods. We solve the radiative transfer equation for grey atmosphere analytically in a pure scattering medium, including local dissipation as an additional heating term in the warm corona. The temperature profile of the warm corona is calculated assuming that it is cooled by Compton scattering, with the underlying dissipative disk providing photons to the corona.
Results. Our analytic calculations show that a dissipative thick corona (τcor in the range 10–12) on top of a standard accretion disk can reach temperatures of the order of 0.5–1 keV in its upper layers provided that the disk is passive. However, in the absence of strong magnetic fields, the requirement of a Compton cooled corona in hydrostatic equilibrium in the vertical direction sets an upper limit on the Thomson optical depth τcor ≲ 5. We show that this value cannot be exceeded independently of the accretion disk parameters. However, magnetic pressure can extend this result to larger optical depths. Namely, a dissipative corona might have an optical depth up to ~20 when the magnetic pressure is 100 times higher than the gas pressure.
Conclusions. The observation of warm coronae with Thomson depth larger than ≃5 puts tight constraints on the physics of the accretion disk/corona systems and requires either strong magnetic fields or vertical outflows to stabilize the system.
Key words: radiative transfer / scattering / methods: analytical / accretion, accretion disks
© ESO, 2015
1. Introduction
Many successful models of the broadband spectra of accreting black holes contain a contribution from a moderately hot, optically thick layer on top of the relatively colder accretion disk. Such a layer is frequently postulated when the broadband spectrum of an accreting system resembles a power law in the soft X-ray band, with the photon index above 2.
Postulating an optically thick hotter medium sandwiching the colder disk inside is in apparent conflict with the results for the radiative transfer in the diffusion approximation. The classical Eddington approximation of the radiative transfer in diffusion approximation shows that the temperature decreases monotonically from the interior towards the surface of an atmosphere (Mihalas 1978). Therefore, the existence of the optically thick corona above the cooler disk interior seems unphysical (Ebisawa et al. 2003). A temperature inversion is usually only obtained in the optically thin zone, where the diffusion approximation does not apply. The best example is the solar corona. Thus, the question arises of whether the cold disk would heat up to reach the same temperature as the optically thick part of the corona.
 |
Fig. 1 Dissipative slab corona on top of the non-dissipative atmosphere of the accretion disk. |
In this paper, we address this question using a very simple analytical model. We consider the vertical structure of the accretion disk/corona that is shown in Fig. 1, and investigate the radiative and pressure equilibrium of the upper layers of the accretion flow as a function of the fraction of the accretion power that is dissipated in the corona. We show that the disk embedded in the hotter optically thick medium does not actually heat up much more than in the case of an optically thin surrounding corona discussed in basic papers such as Haardt & Maraschi (1993) and Svensson & Zdziarski (1994). We check conditions for which an optically thick, Compton cooled zone can exist in hydrostatic equilibrium with a specified underlying colder disk.
The paper is organized as follows: Sect. 2 summarizes observational evidence for the existence of optically thick corona. In Sect. 3 we describe the solution of radiative transfer equation for the grey atmosphere with additional heating. Section 4 describes the temperature structure of this warm skin together with the underlying accretion disk; in Sect. 5 the hydrostatic equilibrium is solved; and in Sect. 6 we show when corona is dominated by Compton cooling. All results are discussed in Sect. 7.
2. Observational evidence for optically thick corona
The standard theory of the Shakura & Sunyaev (1973, hereafter SS disk) accretion disk model predicts that the spectrum of an accretion disk is well modelled as a multi-colour black body, showing an exponential cut-off at high frequencies connected with the maximum of the temperature in the disk atmosphere. Some exceptional quasars/active galaxies and specific spectral states of X-ray binaries selected for the determination of the black hole spin show such a thermal cut-off (Steiner et al. 2011), but in many cases the spectrum continues as a relatively steep/soft power law.
The hard (2–100 keV) X-ray spectra of radio quiet active galactic nuclei (AGN) are generally characterized by a flat power law shape sometimes cut-off around 100 keV (Jourdain et al. 1992; Maisack et al. 1993; Perola et al. 2002; Ballantyne 2014; Malizia et al. 2014, and references therein) and the presence of reflection components (iron line, reflection hump) is commonly observed (Pounds et al. 1990). The soft (below 2 keV) band is generally characterized by an excess with respect to the extrapolation of this hard X-ray power law. This is the so-called soft X-ray excess. When fitted with a power law, it shows a steep (Γ > 2) spectral shape. The origin of this component is still unknown. It could be equally fitted by a blurred ionized reflection (Crummy et al. 2006), a blurred ionized absorption (Gierliński & Done 2004), or by thermal Comptonized emission in a moderately hot, optically thick layer possibly located on the top of the colder accretion disk (Walter & Fink 1993; Magdziarz et al. 1998; Done et al. 2012; Petrucci et al. 2013).
The quasar composite spectra are well explained by such a component, with the photon index Γ ~ 2.5 (Laor et al. 1997; Elvis et al. 2012). The whole class of narrow line Seyfert 1 (NLS1) galaxies has similar soft X-ray slopes. This specific spectral element is observed in galactic sources in the very high state and intermediate state (e.g. Gierliński & Done 2003). The roughly power law shape of this component and the correlation observed between the UV and soft-X-ray bands suggests Comptonization as a mechanism responsible for this emission. Furthermore, observations show that the significant fraction of the bolometric luminosity of the accreting system (~30–50%) is carried out by this emitting layer (Vasudevan et al. 2014).
Usually, it is postulated that the hot medium responsible for this radiation forms a skin or a corona above the inner parts of the accretion disk. This skin or corona is optically thick in many models of specific objects, with Thomson optical depth in the range of 2–20. The observed slope of the soft X-ray spectrum does not determine the optical depth of the scattering medium since it depends on the Compton y parameter, i.e. a combination of the optical depth and the temperature. However, the fact that an unscattered disk component is not required in the fit or the direct detection of the turn-off implies rather low temperature and high optical depth.
Such solutions are usually discussed in the context of specific observational data. White & Holt (1982) required an optically thick corona to explain the temporal and spectral properties of neutron star sources 4U 1822-37, 4U 2729+47, and Cyg X-3 (see also Bayless et al. 2010), although recent papers (e.g. Iaria et al. 2013) argue that the corona is very optically thin and the direct view to the neutron star in 4U 1822-37 is blocked by the outer rim of the accretion disk.
Magdziarz et al. (1998) postulated the presence of a warm optically thick Comptonizing medium to fit the UV-soft X-ray spectrum of NGC 5548. However, they did not expect it to co-exist with the cold disk as a vertical layer; instead, they suggested this medium as a radial transition region between the cold outer disk and a hot inner flow. Zhang et al. (2000) modelled the spectrum of GRO J1655-40 with a warm layer at T = 1.0 keV with the optical thickness τ = 10 located above a cold accretion disk. Indeed, they have considered three vertical layers: a cold disk, a warm skin, and a hot corona. Janiuk et al. (2001) required the presence of a warm corona of optical depth equal to 12 in order to fit the soft X-ray spectrum of a quasar/NLS1 object PG 1211+143. Życki et al. (2001) found coronal temperature ~5 keV and optical depth ~3 from their hybrid models of soft states of X-ray binaries, GS 1124-68 and GS 2000+25, and higher values of optical depth (~10) were implied for some of the very high state data sets. Petrucci et al. (2013) found a soft corona with temperature ~0.5 keV and large optical depth (~20) for the Seyfert 1 galaxy Mrk 509.
Monte Carlo models of hot coronae with large optical depth were calculated by Czerny et al. (2003) in order to explain the broadband spectra of quasar composite spectra, Ton S180, Mrk 359, and PG 1211+143, i.e. high accretion rate AGN. Kubota & Done (2004) obtained good spectral fits with the temperature of the order of 10 keV and optical depth ~2 in the two data sets for VHS of XTE J1 550-564. Jin et al. (2012) successfully fitted the broadband spectra of 51 AGN with a model of accretion disk thermal emission, a low temperature optically thick Comptonization, and a hot optically thin corona. In their fits the electron temperature in the thick corona was in the range of 0.1–2 keV, and the optical depth 4–40 in different objects. The model of the optically thick, low temperature corona surrounding the cold disk was also successfully applied to model the spectrum of a ULX source IC 342 (Ebisawa et al. 2003), although the model was considered rather unphysical by the authors.
3. Grey optically thick scattering medium with dissipation
We are interested in the case of a grey atmosphere with pure scattering (i.e. we neglect emission and absorption). We assume that the atmosphere is optically thick, and therefore adopt the Eddington approximation in the whole medium. We note, that similar approach was made by Farinelli & Titarchuk (2011) in the context of the hot transition layer between the accretion disk and neutron star surface. We allow for an additional dissipation which heats the corona. There are three possible heating mechanisms in such a corona: i) dissipation of waves; ii) magnetic field reconnection; or iii) viscous accretion in the corona. The issue of the quantitative description of the plasma heating is still unsolved even in the case of the solar corona (for a review see Parnell & De Moortel 2012). In magnetohydrodynamical (MHD) accretion disk simulations this lack of knowledge is parametrized as an effective viscosity of unspecified nature (e.g. Hirose & Turner 2011). The fraction of the energy dissipated in the corona, predicted by MHD, depends strongly on the details of the computations (for a review see Blaes 2014). It ranges from about 25% Miller & Stone (2000) to only a small fraction (Hirose et al. 2009), but the magnetic buoyancy effect can increase it (Blaes et al. 2011).
For simplicity, we assume that the input energy rate per unit optical depth (and solid angle), Q is uniform from the surface (τ = 0) to the base of the corona (τ = τcor). This corona is located above a cold accretion disk, which itself dissipates energy due to the accretion flow. The assumption that all dissipated energy is emitted in the form of radiation allows us to derive a simple fully analytical solution for the local vertical temperature structure. At the surface of the corona the escaping radiation flux 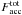 is the sum of the flux generated through internal dissipation inside the accretion disk, Fdisk, and that produced through dissipation in the corona, Fcor:
is the sum of the flux generated through internal dissipation inside the accretion disk, Fdisk, and that produced through dissipation in the corona, Fcor: 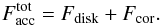 (1)The assumption that the heating of the corona is uniform gives:
(1)The assumption that the heating of the corona is uniform gives: 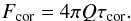 (2)Additionally, we define a convenient parameter,
(2)Additionally, we define a convenient parameter, 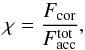 (3)which is the fraction of the total accretion power that is dissipated in the corona.
(3)which is the fraction of the total accretion power that is dissipated in the corona.
The frequency-integrated radiation transfer equation with an additional energy input Q can be written as 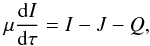 (4)where μ is the cosine of azimuthal angle. The optical depth, τ is measured downward, from the top of the corona toward the disk, I(μ,τ) is the radiation intensity, and J(τ) is the mean intensity. The third term on the right hand side modifies the source function, S, and describes the increase in the photon energy due to the dissipation within the corona (S = J + Q). Following the standard Eddington approach, we can derive the solution of the radiative transfer equation by calculating its first moments, i.e. integrating over solid angles. The zeroth moment gives
(4)where μ is the cosine of azimuthal angle. The optical depth, τ is measured downward, from the top of the corona toward the disk, I(μ,τ) is the radiation intensity, and J(τ) is the mean intensity. The third term on the right hand side modifies the source function, S, and describes the increase in the photon energy due to the dissipation within the corona (S = J + Q). Following the standard Eddington approach, we can derive the solution of the radiative transfer equation by calculating its first moments, i.e. integrating over solid angles. The zeroth moment gives 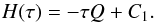 (5)The integration constant C1 represents the Eddington flux at the top of the corona (τ = 0), which is, by definition,
(5)The integration constant C1 represents the Eddington flux at the top of the corona (τ = 0), which is, by definition, 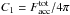 . Using Eqs. (2) and (3), the Eddington flux profile can then be written as
. Using Eqs. (2) and (3), the Eddington flux profile can then be written as 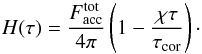 (6)We note that at τ = τcor where the corona touches the cold disk, the downward flux corresponding to the illumination of the disk by the corona cancels out the upward flux of reprocessed/reflected radiation from the disk. Therefore, the net radiation flux at τcor is only that caused by internal dissipation in the cold disk Fdisk.
(6)We note that at τ = τcor where the corona touches the cold disk, the downward flux corresponding to the illumination of the disk by the corona cancels out the upward flux of reprocessed/reflected radiation from the disk. Therefore, the net radiation flux at τcor is only that caused by internal dissipation in the cold disk Fdisk.
The first moment of the radiation transfer is 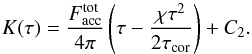 (7)In the Eddington approximation, we accept K = J/ 3 at every optical depth across the medium. In addition, at the corona surface we have only outgoing radiation flux, as in standard stellar atmosphere, so we have the condition J(0) = 2H(0), which allows the constant C2 to be determined. Setting τ = 0 in Eqs. (6) and (7) we get
(7)In the Eddington approximation, we accept K = J/ 3 at every optical depth across the medium. In addition, at the corona surface we have only outgoing radiation flux, as in standard stellar atmosphere, so we have the condition J(0) = 2H(0), which allows the constant C2 to be determined. Setting τ = 0 in Eqs. (6) and (7) we get 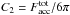 , so that the mean intensity as a function of the optical depth in the optically thick corona is given by the expression
, so that the mean intensity as a function of the optical depth in the optically thick corona is given by the expression 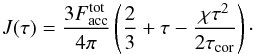 (8)Equations (6)–(8) are valid only in the warm corona (i.e. for τ<τcor) and they are largely independent of the underlying accretion disk structure. However, the same formalism can be used to extend these solutions deeper in the disk atmosphere in order to investigate the effects of the presence of the corona on the upper layers of the accretion disk.
(8)Equations (6)–(8) are valid only in the warm corona (i.e. for τ<τcor) and they are largely independent of the underlying accretion disk structure. However, the same formalism can be used to extend these solutions deeper in the disk atmosphere in order to investigate the effects of the presence of the corona on the upper layers of the accretion disk.
As in the standard SS 1D disk, all flux is generated close to the equatorial plane (Różańska 1999), we can neglect dissipation in the disk atmosphere, and assume that all the disk flux is generated below this layer at deeper optical depth (τ ≳ 105), see Fig. 1. Here we consider only the properties of the upper non-dissipative atmosphere. For simplicity, we will not solve the flux dissipation equation down to the midplane as this would not change our final result of temperature profile on the border of the warm corona and the disk.
The solution of Eq. (4) with Q = 0, implies a constant Eddington flux below the corona. Then the value of the flux at τcor sets the value of H everywhere in the disk atmosphere: 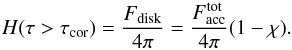 (9)The first moment of the radiation transfer then gives
(9)The first moment of the radiation transfer then gives 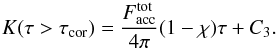 (10)The constant C3 is determined from the condition of continuity of K (and J) at τcor:
(10)The constant C3 is determined from the condition of continuity of K (and J) at τcor: 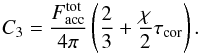 (11)And finally the mean intensity in the disk atmosphere is
(11)And finally the mean intensity in the disk atmosphere is ![\begin{equation} J(\tau>\tau_{\rm cor})= \frac{3F_{\rm acc}^{\rm tot}}{4\pi}\left[(1-\chi)\tau +\frac{\chi}{2}\tau_{\rm cor}+\frac{2}{3}\right] \cdot \label{eq:jda} \end{equation}](/articles/aa/full_html/2015/08/aa26288-15/aa26288-15-eq50.png) (12)We note that in the absence of a corona (χ = 0) this equation reduces to the standard mean intensity profile of grey atmospheres:
(12)We note that in the absence of a corona (χ = 0) this equation reduces to the standard mean intensity profile of grey atmospheres: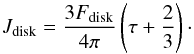 (13)In the presence of a warm corona, there is an additional component Jcor to the mean intensity of the disk that is due to the illumination of the atmosphere by the corona, J = Jdisk + Jcor, which is
(13)In the presence of a warm corona, there is an additional component Jcor to the mean intensity of the disk that is due to the illumination of the atmosphere by the corona, J = Jdisk + Jcor, which is 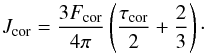 (14)The typical vertical structure of the radiation properties of the corona/disk atmosphere system is shown in Fig. 2.
(14)The typical vertical structure of the radiation properties of the corona/disk atmosphere system is shown in Fig. 2.
 |
Fig. 2 Typical radiation structure of the accretion disk corona and upper disk atmosphere. The upper panel shows the assumed dissipation profile, the middle and lower panel show the resulting radiation flux and pressure profiles, respectively. |
4. Temperature profile
The next step is to determine the temperature profile across the disk and corona using mean intensity field. The temperature profile is derived assuming that matter is in equilibrium with the radiation field. The resulting temperature depends on the radiative cooling mechanism operating in the gas.
4.1. Temperature profile in the warm corona
The radiative transfer solution for grey atmosphere does not specify the temperature profile in a purely scattering medium, which is the case of the soft corona, i.e. for τ<τcor. However, we can obtain the temperature profile taking into account that the scattered photons must cool the corona through Comptonization in order to have the thermal heating/cooling balance.
When cooling is dominated by inverse Compton scattering in the Thomson regime by a thermal population of sub-relativistic temperature, the balance between cooling and heating reads 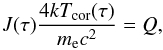 (15)where Tcor is the corona temperature, c the velocity of light, k the Boltzmann constant, and me the electron rest mass.
(15)where Tcor is the corona temperature, c the velocity of light, k the Boltzmann constant, and me the electron rest mass.
 |
Fig. 3 Temperature profiles in the disk/corona system for the various values of the parameters χ, τcor of the six fiducial models listed in Table 1. Each curve is labelled with its model reference number, corresponding to that given in Table 1. |
Since J is an increasing function of the optical depth (see Eq. (8)) and Q is assumed to be a constant, the electron temperature decreases with τ, showing a temperature inversion: 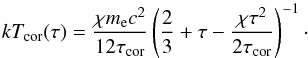 (16)The temperature remains hot from the coronal surface down to τ = 2/3, then it slowly decreases. Depending on the amount of dissipated energy, the soft corona can be quite hot down to moderate optical depth. The vertical temperature profile of the soft corona above the cold disk is determined by only two parameters: the total optical depth τcor of the skin/corona, and the fraction χ of flux dissipated inside the corona to the total flux dissipated inside the disk and corona. In Fig. 3 we show examples of full temperature profiles for different values of these parameters. We note, that this profile comes strictly from the radiation properties and does not imply that the hydrostatic equilibrium is satisfied in this multi-zone structure. We address this issue in the following section.
(16)The temperature remains hot from the coronal surface down to τ = 2/3, then it slowly decreases. Depending on the amount of dissipated energy, the soft corona can be quite hot down to moderate optical depth. The vertical temperature profile of the soft corona above the cold disk is determined by only two parameters: the total optical depth τcor of the skin/corona, and the fraction χ of flux dissipated inside the corona to the total flux dissipated inside the disk and corona. In Fig. 3 we show examples of full temperature profiles for different values of these parameters. We note, that this profile comes strictly from the radiation properties and does not imply that the hydrostatic equilibrium is satisfied in this multi-zone structure. We address this issue in the following section.
One-zone Comptonization models such as those used to derive the observational properties on the warm corona only constrain the average temperature of the skin, without any constraints on the temperature stratification. Since in our models temperature changes with optical depth, we should compare the value of the average temperature of the warm skin weighted by its optical depth with that determined from observations, 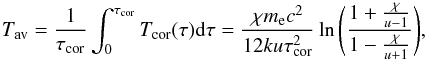 (17)where
(17)where 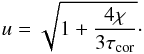 (18)In the limit of large τcor, the average temperature given by Eq. (17) can be approximated within 10% (for τcor> 3) as
(18)In the limit of large τcor, the average temperature given by Eq. (17) can be approximated within 10% (for τcor> 3) as 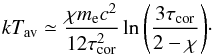 (19)The dependence of the average coronal temperature on τcor is plotted in Fig. 4 for several values of the χ parameter. We can clearly see that a warm skin cooled by Comptonization can be produced even for large values of the coronal optical depth provided that most of the accretion power is dissipated in the warm corona. However, the coronal temperature decreases with decreasing χ and increasing τcor.
(19)The dependence of the average coronal temperature on τcor is plotted in Fig. 4 for several values of the χ parameter. We can clearly see that a warm skin cooled by Comptonization can be produced even for large values of the coronal optical depth provided that most of the accretion power is dissipated in the warm corona. However, the coronal temperature decreases with decreasing χ and increasing τcor.
 |
Fig. 4 Average coronal temperature vs. optical depth. The full curves show the dependence of the average coronal temperature on the total optical depth of the corona for various values of the fraction of total power dissipated in the corona, χ, as labelled. The dashed curves represent the hydrostatic equilibrium solutions providing the largest possible Thomson depth of the Compton cooled corona for a given χ and magnetic-to-gas-pressure ratio βm (see Sect. 6). Each of the dashed curves shows the track of the solutions in the kTav-τcor plane for a fixed value of βm (as labelled) when χ is varying. |
As a consequence, at small χ (i.e. strong disk dissipation) a hot corona with pure scattering is only consistent with the most moderate observations (i.e. τcor of the order of a few). From the energy equilibrium requirement we can produce a layer of Tcor ~ 0.5 − 1 keV and large Thomson depth 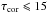 only if most of the accretion power is dissipated in the layer. This appears to be consistent with the observational results of Petrucci et al. (2013) in the case of Mrk 509. These authors infer such parameters for the soft corona and also argue that the observed relative luminosity of the disk and soft corona implies that the disk is passive (i.e. χ ≃ 1). The case of a passive disk provides the maximum achievable temperature for a given coronal depth. We note that some numerical simulations of accretion disks also show a stronger dissipation in the outer layers of the disk (Hirose & Turner 2011).
only if most of the accretion power is dissipated in the layer. This appears to be consistent with the observational results of Petrucci et al. (2013) in the case of Mrk 509. These authors infer such parameters for the soft corona and also argue that the observed relative luminosity of the disk and soft corona implies that the disk is passive (i.e. χ ≃ 1). The case of a passive disk provides the maximum achievable temperature for a given coronal depth. We note that some numerical simulations of accretion disks also show a stronger dissipation in the outer layers of the disk (Hirose & Turner 2011).
We also note that the method presented here is reasonably accurate. Our results can be compared for example to the Monte Carlo simulations presented in Malzac et al. (2001), in the case of a slab corona with Thomson depth of τcor = 3 above a passive disk. They obtained an average temperature ≃9 keV (see their Fig. 2), which is in excellent agreement with the present results. On the other hand, for optically thin coronae the temperature becomes mildly relativistic, our approximations break down, and the simple analytical model underestimates radiation cooling. For τcor = 0.5 and χ = 1, Eq. (17) gives kTav ≃ 103 keV while Malzac et al. (2001) obtain kTav ≃ 70 keV with their detailed calculation.
The above results assume a uniform dissipation rate Q versus optical depth. Recent work based in MHD simulations tend to show that the dissipation per unit mass may vary significantly with altitude (e.g. Jiang et al. 2014; Begelman et al. 2015). Although the dissipation profile is highly model dependent, we have also studied the coronal properties for a few ad hoc, non-uniform dissipation profiles. These preliminary results show that although the temperature profile depends on the exact dissipation profile, the averaged temperature does not.
We neglect synchrotron photons, thermal conduction and ionization in the warm skin, but we have checked that those processes are not important comparing to Comptonization. Generally, synchrotron radiation is efficient at very high temperature and highly magnetized plasma, which is not our case. It was shown that it is important in non-thermal sources (Wardziński & Zdziarski 2000), which we do not consider. On the other hand, emission of synchrotron photons can produce additional soft photons, which can be up-scattered, but those photons are too cool to contribute significantly to the radiation energy density. Thermal conduction fronts are always very narrow. We have estimated that the conduction flux for our resulting temperature profile is about 7 orders of magnitude lower than the flux generated by accretion. The value of ionization/recombination cooling was always lower than the Compton cooling for the gas temperature of the order of 1 keV, without external illumination (Różańska & Czerny 1996).
4.2. Temperature profile in the disk atmosphere
Deep in the optically thick atmosphere of the disk (τ>τcor) we can assume that radiation is fully thermalized (J = σT4/π, where σ is the Stefan constant). Using Eq. (12), we obtain the following temperature structure: ![\begin{equation} T_{\rm atm}^4= \frac{3F_{\rm acc}^{\rm tot}}{4\sigma} \left[(1-\chi)\tau+ \frac{2}{3}+\frac{\chi\tau_{\rm cor}}{2}\right]\cdot \label{eq:tther1} \end{equation}](/articles/aa/full_html/2015/08/aa26288-15/aa26288-15-eq90.png) (20)This expression can be rewritten as
(20)This expression can be rewritten as 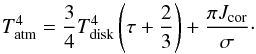 (21)The first term on the right hand side of Eq. (21) corresponds to the standard temperature structure for fully thermalized grey atmosphere in the Eddington approximation. The parameter Tdisk is the disk effective temperature in the absence of a warm corona, calculated from the intrinsic disk flux Fdisk. The constant second term represents the increase in disk temperature due to the coronal illumination.
(21)The first term on the right hand side of Eq. (21) corresponds to the standard temperature structure for fully thermalized grey atmosphere in the Eddington approximation. The parameter Tdisk is the disk effective temperature in the absence of a warm corona, calculated from the intrinsic disk flux Fdisk. The constant second term represents the increase in disk temperature due to the coronal illumination.
Unlike Tcor, the temperature profile of the disk atmosphere, Tatm, depends on the accretion flux 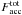 . Using standard accretion disk theory,
. Using standard accretion disk theory, 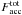 can be estimated as a function of the mass of the black hole MBH, and Eddington luminosity fraction ṁ = L/LEdd at a given radius R = rGMBH/c2,
can be estimated as a function of the mass of the black hole MBH, and Eddington luminosity fraction ṁ = L/LEdd at a given radius R = rGMBH/c2, 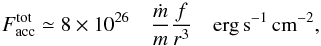 (22)where m = MBH/M⊙,
(22)where m = MBH/M⊙, 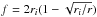 and ri is the inner radius of the disk expressed in gravitational radii.
and ri is the inner radius of the disk expressed in gravitational radii.
In Fig. 3 the profile in the disk atmosphere was calculated for a black hole of mass MBH = 1.4 × 108M⊙ (Liu 1983) at 10 gravitational radii from the black hole and at an accretion rate equal to 2% of the Eddington accretion rate. For these parameters the accretion flux is 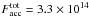 erg s-1 cm-2. As can be seen in Fig. 3, the temperature profile in the upper layers of the disk flattens and departs from the standard grey atmosphere temperature profile due to the strong coronal illumination only when most of the power is dissipated in the warm corona.
erg s-1 cm-2. As can be seen in Fig. 3, the temperature profile in the upper layers of the disk flattens and departs from the standard grey atmosphere temperature profile due to the strong coronal illumination only when most of the power is dissipated in the warm corona.
The absorption of coronal photons by the cold disk only slightly increases disk effective temperature, which remains significantly lower than that of the corona. Owing to additional dissipation in the soft corona, all temperature profiles show a strong temperature inversion in the disk/corona system. At the transition between the disk and corona there is a discontinuity due to the change in cooling mechanism. The amplitude of the temperature jump can be estimated as ![\begin{equation} \left. \frac{T_{\rm atm}}{T_{\rm cor}} \right|_{\tau=\tau_{\rm cor}} \simeq 0.12 \left( \frac{\dot{m}}{m} \frac{f}{r^3}\right)^{1/4} \frac{\tau_{\rm cor}}{\chi}\left[\frac{2}{3}+\tau_{\rm cor}\left(1-\frac{\chi}{2}\right)\right]^{5/4} \cdot \end{equation}](/articles/aa/full_html/2015/08/aa26288-15/aa26288-15-eq102.png) (23)This ratio remains lower than unity over a very broad range of black hole masses, mass accretion rates, and disk radii. In practice, only when χ vanishes, the temperature of the disk at τcor can become comparable to or even hotter than that of the corona.
(23)This ratio remains lower than unity over a very broad range of black hole masses, mass accretion rates, and disk radii. In practice, only when χ vanishes, the temperature of the disk at τcor can become comparable to or even hotter than that of the corona.
We note that in reality the change in cooling mechanism might not be as abrupt as we have assumed here, and that the temperature discontinuity could be smoothed. The computations of the disk/corona transitions are difficult; however, it appears that the temperature drop is always very sharp even if all the radiation processes are fully taken into account (Madej & Różańska 2000b; Ballantyne et al. 2001; Nayakshin & Kallman 2001; Różańska et al. 2002).
5. Hydrostatic equilibrium for the corona/disk system
The question arises whether such a two-zone system can be in hydrostatic equilibrium. Here we derive analytical formulae for the pressure profile in the disk-corona system. We use the standard equation of vertical hydrostatic equilibrium in a geometrically thin disk (Madej & Różańska 2000a). The total pressure P is the sum of the gas pressure Pgas, the radiation pressure Prad, and the magnetic pressure Pmag. Locally, the total pressure has to balance the gravitational force, 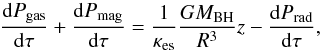 (24)where G is the gravitational constant, and κes is the Thomson scattering cross section. In a general approach the total opacity should be taken into account, but for simplicity we take only Thomson scattering into account and set κes = 0.34 cm2 g-1. In order to obtain analytical solutions, we assume that the warm corona is geometrically thin compared to the scale-height of the disk Zdisk, so that the vertical distance to the equatorial plane z can be considered a constant z = Zdisk. This implies that the gravitational force is constant along the vertical direction inside the corona and the upper layers of the disk.
(24)where G is the gravitational constant, and κes is the Thomson scattering cross section. In a general approach the total opacity should be taken into account, but for simplicity we take only Thomson scattering into account and set κes = 0.34 cm2 g-1. In order to obtain analytical solutions, we assume that the warm corona is geometrically thin compared to the scale-height of the disk Zdisk, so that the vertical distance to the equatorial plane z can be considered a constant z = Zdisk. This implies that the gravitational force is constant along the vertical direction inside the corona and the upper layers of the disk.
For the grey atmosphere, the radiation pressure gradient depends on the flux expressed in Eq. (6) for the corona and Eq. (9) for the disk atmosphere: 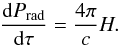 (25)
(25)
5.1. Pressure and density profile in the warm corona
In the corona, the radiation pressure profile is obtained directly from Eq. (8): 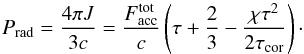 (26)We assume a uniform magnetic to gas pressure ratio βm:
(26)We assume a uniform magnetic to gas pressure ratio βm: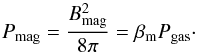 (27)In our approach, the coronal dissipation, Q is not connected to the magnetic pressure parameter for simplicity. This coupling would require a numerical treatment of the problem (see e.g. Begelman et al. 2015). Solving the equation of hydrostatic equilibrium (24), we find an expression for the gas pressure structure assuming, as a boundary condition, that Pgas(τ = 0) = 0,
(27)In our approach, the coronal dissipation, Q is not connected to the magnetic pressure parameter for simplicity. This coupling would require a numerical treatment of the problem (see e.g. Begelman et al. 2015). Solving the equation of hydrostatic equilibrium (24), we find an expression for the gas pressure structure assuming, as a boundary condition, that Pgas(τ = 0) = 0, 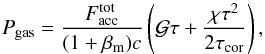 (28)where the constant
(28)where the constant 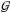 represents the ratio of the pressure forces of the gas and magnetic field to that of radiation at the surface of the corona:
represents the ratio of the pressure forces of the gas and magnetic field to that of radiation at the surface of the corona: 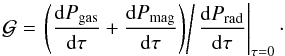 (29)The radiation pressure force dominates the support of the corona at all depths for
(29)The radiation pressure force dominates the support of the corona at all depths for 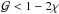 . The value of
. The value of 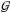 can also be expressed as
can also be expressed as 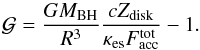 (30)The first term on the right hand side of Eq. (30) is the ratio of the gravitational to radiation pressure force at the surface of the corona. For a corona in hydrostatic equilibrium this ratio is necessarily larger than unity and consequently
(30)The first term on the right hand side of Eq. (30) is the ratio of the gravitational to radiation pressure force at the surface of the corona. For a corona in hydrostatic equilibrium this ratio is necessarily larger than unity and consequently 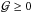 . The half of the disk thickness Zdisk is a crucial parameter that controls the hydrostatic equilibrium in the vertical direction (Różańska et al. 1999). The case where
. The half of the disk thickness Zdisk is a crucial parameter that controls the hydrostatic equilibrium in the vertical direction (Różańska et al. 1999). The case where 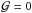 gives the minimum disk thickness, for which the total disk pressure can be balanced by the gravitational force:
gives the minimum disk thickness, for which the total disk pressure can be balanced by the gravitational force: 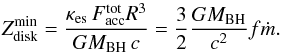 (31)For a thinner disk, the matter will be outflowing from the system (Witt et al. 1997).
(31)For a thinner disk, the matter will be outflowing from the system (Witt et al. 1997).
The density profile clearly depends on the assumed disk geometrical thickness Zdisk, and we can derive this density from the equation of state as 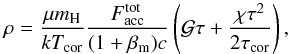 (32)where μ is a mean molecular weight assumed to be 0.5, and mH is the mass of hydrogen atom. The density increases with τ, and from Eq. (32) we see that setting the disk parameter
(32)where μ is a mean molecular weight assumed to be 0.5, and mH is the mass of hydrogen atom. The density increases with τ, and from Eq. (32) we see that setting the disk parameter 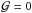 (or equivalently
(or equivalently 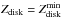 ) minimizes the density in the corona. This is illustrated in Fig. 5, which gives examples of density profiles obtained for the parameters listed in Table 1.
) minimizes the density in the corona. This is illustrated in Fig. 5, which gives examples of density profiles obtained for the parameters listed in Table 1.
5.2. Pressure and density profiles in the disk atmosphere
 |
Fig. 5 Density profile around the disk corona transition for the six fiducial models detailed in Table 1. The curves are labelled by their model number. |
The pressure and density profiles in the disk atmosphere below the corona (τ>τcor) can be estimated in a similar way. The radiation pressure profile is given by Eq. (12): ![\begin{equation} P_{\rm rad}= \frac{F_{\rm acc}^{\rm tot}}{c}\left[(1-\chi)\tau +\frac{\chi}{2}\tau_{\rm cor}+\frac{2}{3}\right] \cdot \label{eq:pda} \end{equation}](/articles/aa/full_html/2015/08/aa26288-15/aa26288-15-eq129.png) (33)The pressure equilibrium Eq. (24) is solved using Eq. (9) and assuming continuity of pressure at the disk/corona transition:
(33)The pressure equilibrium Eq. (24) is solved using Eq. (9) and assuming continuity of pressure at the disk/corona transition: ![\begin{equation} P_{\rm gas}= \frac{F_{\rm acc}^{\rm tot}}{(1+\beta_{\rm m})c}\left[(\mathcal{G}+\chi)\tau-\frac{\chi}{2}\tau_{\rm cor}\right] . \end{equation}](/articles/aa/full_html/2015/08/aa26288-15/aa26288-15-eq130.png) (34)The density profile follows:
(34)The density profile follows: ![\begin{equation} \rho = {{\mu m_{\rm H}} \over kT_{\rm atm}} {F_{\rm acc}^{\rm tot} \over (1+\beta_{\rm m}) c} \left[(\mathcal{G}+\chi)\tau-\frac{\chi}{2}\tau_{\rm cor}\right]. \label{eq:rhoatm} \end{equation}](/articles/aa/full_html/2015/08/aa26288-15/aa26288-15-eq131.png) (35)Figure 5 shows some examples of density profiles around the disk transitions for our fiducial value of the total accretion flux. In all cases, we observe a discontinuity in density at τcor which has the same amplitude as the temperature jump discussed in the Sect. 4.2. Owing to the temperature jump and the condition of pressure equilibrium at the disk/corona transition, the disk atmosphere tends to be much denser than the corona.
(35)Figure 5 shows some examples of density profiles around the disk transitions for our fiducial value of the total accretion flux. In all cases, we observe a discontinuity in density at τcor which has the same amplitude as the temperature jump discussed in the Sect. 4.2. Owing to the temperature jump and the condition of pressure equilibrium at the disk/corona transition, the disk atmosphere tends to be much denser than the corona.
5.3. Limitations
In Sect. 5 we have estimated the properties of a warm corona and disk atmosphere in pressure equilibrium. Our proposed treatment has the advantage of being very simple. The drawbacks of this simplicity are some limitations that we now briefly discuss.
First, although the effects of the disk on the corona and disk atmosphere is taken into account via the 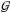 parameter, the present approach does not allow us to guarantee that there is indeed a disk solution below the atmosphere that both has the required
parameter, the present approach does not allow us to guarantee that there is indeed a disk solution below the atmosphere that both has the required 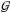 parameter and connects smoothly to the atmosphere. A full calculation of the vertical stratification of the disk down to the mid-plane, also including dissipation, would be required in order to obtain such self-consistent solutions and to calculate Zdisk from first principles.
parameter and connects smoothly to the atmosphere. A full calculation of the vertical stratification of the disk down to the mid-plane, also including dissipation, would be required in order to obtain such self-consistent solutions and to calculate Zdisk from first principles.
In addition, we note that for the density profiles with the lowest densities in the corona, our assumption of constant gravity may be inaccurate. For these profiles the scale height of the corona, 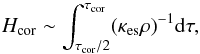 (36)can be comparable to or even larger than Zdisk. In this case the gravity at the surface of the corona is significantly larger than at the bottom. Taking into account the height dependent gravity would require a numerical resolution of the equilibrium which is beyond the scope of this paper, but we can anticipate its effects. Indeed, if we assume that the disk/corona transition is located at a height Zdisk, the increased gravity force in the upper corona will necessitate a higher pressure in order to sustain the equilibrium, and as a consequence the coronal density will also be increased compared to our current estimates. In particular, this effect may affect our results for small Zdisk (or small
(36)can be comparable to or even larger than Zdisk. In this case the gravity at the surface of the corona is significantly larger than at the bottom. Taking into account the height dependent gravity would require a numerical resolution of the equilibrium which is beyond the scope of this paper, but we can anticipate its effects. Indeed, if we assume that the disk/corona transition is located at a height Zdisk, the increased gravity force in the upper corona will necessitate a higher pressure in order to sustain the equilibrium, and as a consequence the coronal density will also be increased compared to our current estimates. In particular, this effect may affect our results for small Zdisk (or small 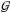 ), which may underestimate the pressure and the density in the corona by a factor of 2–3.
), which may underestimate the pressure and the density in the corona by a factor of 2–3.
Finally, our calculation of the pressure equilibrium assumes that the opacity is dominated by electron scattering. If absorption becomes important, both pressure and density will be lower than our simple estimates. We have checked a posteriori that for the fiducial models presented in Figs. 3 and 5, the Kramer free-free absorption opacity κff ≃ 6 × 1022ρT− 7/2 cm2 g-1 is negligible compared to κes both in the corona and in the atmosphere of the disk. For these models our estimated pressure profiles are not affected by the approximation of a pure scattering medium. We stress, however, that since even in the disk atmosphere the medium is only weakly absorbing, the assumption of fully thermalized radiation used to infer the temperature profile of the atmosphere may break down close to the disk/corona transition, making the transition much more gradual than our simplified calculation suggests.
A detailed investigation of all these issues is deferred to future works.
6. Constraints from the requirement of a Compton cooled corona
In the previous sections we have determined the temperature, pressure and density profile of the corona under the assumption that the dominant cooling mechanism is Compton scattering. This assumption was motivated by observational results based on modelling the coronal emission with Comptonization models. We now have to determine the parameter regimes for which this assumption remains valid. In addition to Compton cooling, the most efficient cooling mechanism is expected to be bremsstrahlung, which must remain negligible compared to Compton cooling. Here we estimate the ratio of Compton cooling rate ΛC = 16πkT/ (mec2) ρκesJ(τ) in erg/s/cm3, to the bremsstrahlung cooling rate ΛB = Bρ2T1/2, where B = 6.6 × 1020 CGS units. This ratio must remain larger than unity across the soft corona. Using Eqs. (8) and (16) we get the condition 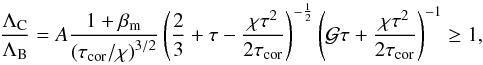 (37)with the constant
(37)with the constant 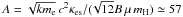 . The above ratio is a decreasing function of optical depth, therefore the condition in Eq. (37) is verified in the whole corona if it is verified at τ = τcor. The maximum possible Thomson depth for a Compton cooled corona is obtained by setting the condition that the depth τcor corresponds to the transition between Compton dominated and bremsstrahlung dominated regions, i.e. by solving ΛC/ ΛB|τ = τcor = 1. The coronal optical depth of the fiducial models of Table 1 leading to the profiles presented in Figs. 3 and 5 were determined in this way and correspond to the deepest possible Compton corona for the given set of χ, βm, and
. The above ratio is a decreasing function of optical depth, therefore the condition in Eq. (37) is verified in the whole corona if it is verified at τ = τcor. The maximum possible Thomson depth for a Compton cooled corona is obtained by setting the condition that the depth τcor corresponds to the transition between Compton dominated and bremsstrahlung dominated regions, i.e. by solving ΛC/ ΛB|τ = τcor = 1. The coronal optical depth of the fiducial models of Table 1 leading to the profiles presented in Figs. 3 and 5 were determined in this way and correspond to the deepest possible Compton corona for the given set of χ, βm, and  .
.
From Eq. (37), we also see that the case of  , or equivalently
, or equivalently 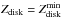 , gives the most favourable condition to have a purely Compton cooled corona because it corresponds to the minimum of the gas pressure and density. Therefore, in order to find regimes where our assumptions fail, it is enough to calculate this ratio at the base of corona for
, gives the most favourable condition to have a purely Compton cooled corona because it corresponds to the minimum of the gas pressure and density. Therefore, in order to find regimes where our assumptions fail, it is enough to calculate this ratio at the base of corona for 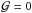 :
: 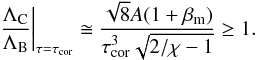 (38)We stress that this equation represents the necessary condition for the Compton cooling dominance and does not depend on any disk parameters.
(38)We stress that this equation represents the necessary condition for the Compton cooling dominance and does not depend on any disk parameters.
 |
Fig. 6 The importance of Compton scattering over the bremsstrahlung at the base of corona as a function of τcor (Eq. (38)). Solid lines in each package are computed for various values of χ = 0.18,0.26,0.40,0.57,0.67 and 0.86. Each package is calculated for three different values of magnetic pressure: βm = 0,10 and 100. The horizontal dashed line represents the case where ΛC/ ΛB = 1, while vertical dotted lines mark values of coronal optical depth for which it happens. |
Figure 6 shows the Compton-to-bremsstrahlung cooling ratios as a function of coronal optical depth for three different values of magnetic pressure in the case 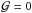 . For each value of βm we consider various values of χ to show the marginal influence of this parameter. We see that the maximum possible Thomson depth of the corona in the case
. For each value of βm we consider various values of χ to show the marginal influence of this parameter. We see that the maximum possible Thomson depth of the corona in the case 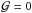 provides an absolute upper limit on the depth of the corona. This upper limit can be estimated as
provides an absolute upper limit on the depth of the corona. This upper limit can be estimated as 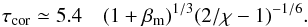 (39)The corresponding average temperature of this deepest possible corona can then be estimated using Eq. (19):
(39)The corresponding average temperature of this deepest possible corona can then be estimated using Eq. (19): ![\begin{equation} kT_{\rm av}\simeq 4 \, \frac{\chi^{\frac{2}{3}}(2-\chi)^{\frac{1}{3}}}{(1+\beta_{\rm m})^{\frac{2}{3}}} \left[1-1.2\times 10^{-4} \ln{\frac{\chi^{-1}(2-\chi)^7 }{(1+\beta_{\rm m})^{2}}}\right] \, {\rm keV.} \end{equation}](/articles/aa/full_html/2015/08/aa26288-15/aa26288-15-eq147.png) (40)Equation (39) shows that when magnetic pressure is zero, bremsstrahlung becomes the dominant emission process as soon as τcor ≳ 5. Such solutions are therefore inconsistent with an unmagnetized, static, Compton dominated, hot, and optically thick coronae. Relaxing one of these constraints might produce a consistent solution. For instance, the corona might not be in static equilibrium. The case of outflowing coronae (Witt et al. 1997) in the frame of our model will be investigated in a future work.
(40)Equation (39) shows that when magnetic pressure is zero, bremsstrahlung becomes the dominant emission process as soon as τcor ≳ 5. Such solutions are therefore inconsistent with an unmagnetized, static, Compton dominated, hot, and optically thick coronae. Relaxing one of these constraints might produce a consistent solution. For instance, the corona might not be in static equilibrium. The case of outflowing coronae (Witt et al. 1997) in the frame of our model will be investigated in a future work.
Alternatively, additional magnetic pressure helps the gas pressure to balance gravity. Hence it produces solutions with lower density, i.e. with lower bremsstrahlung cooling rate. Figure 4 maps the iso-contours of χ and βm for the deepest possible corona in the τcor versus kTav plane. This diagram allows one to estimate the minimum value of the magnetic field pressure ratio required in order to produce a corona with a given optical depth and temperature. For instance, the warm corona recently observed in Mrk 509 by Petrucci et al. (2013), with optical thickness τcor ~ 15 and temperature Tav ≃ 0.5 keV, implies magnetic to gas pressure ratio βm> 30. For MBH = 1.4 × 108M⊙, a distance of 10 gravitational radii, and an accretion rate equal to 2% of the Eddington accretion rate, this implies that the average magnetic field in the corona must be larger than 103 G.
Since the calculations are based on the assumption of 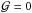 , they provide the necessary conditions for the Compton cooling condition to be satisfied. If Compton cooling dominance is not obtained, no change of Zdisk will save the situation, and if Compton cooling dominance is obtained, there is always a range of
, they provide the necessary conditions for the Compton cooling condition to be satisfied. If Compton cooling dominance is not obtained, no change of Zdisk will save the situation, and if Compton cooling dominance is obtained, there is always a range of 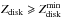 for which the hydrostatic equilibrium is sustained and density is low enough for Compton cooling to dominate over bremsstrahlung cooling. We note however that in the case of minimal density in the corona (
for which the hydrostatic equilibrium is sustained and density is low enough for Compton cooling to dominate over bremsstrahlung cooling. We note however that in the case of minimal density in the corona (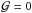 ) our approximation of constant gravity force in the vertical direction can break down (see Sect. 5.1). As a consequence, our simple calculations may underestimate the density and bremsstrahlung cooling rate. Relaxing the assumption of constant gravity may reduce the maximum possible Thomson depth of the corona and/or require even stronger magnetic fields to maintain the dominance of Compton cooling.
) our approximation of constant gravity force in the vertical direction can break down (see Sect. 5.1). As a consequence, our simple calculations may underestimate the density and bremsstrahlung cooling rate. Relaxing the assumption of constant gravity may reduce the maximum possible Thomson depth of the corona and/or require even stronger magnetic fields to maintain the dominance of Compton cooling.
7. Discussion and conclusion
In this paper, we put constraints on the existence of a warm, dissipating, optically thick, and Compton cooled corona in hydrostatic equilibrium with a cold accretion disk. In our computations of the hydrostatic equilibrium in the vertical direction, the radiation pressure component is fully taken into account, contrary to numerical simulations by Schnittman et al. (2013), Uzdensky (2013).
Our simple analytical solution for the warm and dissipative corona above the cold disk shows that a stable temperature inversion is possible in the optically thick case, contrary to the intuitive expectations based on the diffusion approximation, because the solution of purely scattering atmosphere does not specify the temperature. It only gives the radiation density, which rises with the optical depth, as expected. The temperature in the warm corona is determined a posteriori from Compton cooling balance and the temperature increases toward the warm skin surface. We have shown that such a corona can reach temperatures of 0.5–1 keV for assumed values of constant dissipation in the skin of moderate optical depth (τcor< 10). The most extreme parameters e.g. a coronal temperature 0.5 keV at optical depth 15–20, which is observed in the case of Mrk 509 (Petrucci et al. 2013), can also be reproduced provided that the disk is passive (i.e. almost all of the accretion power is dissipated in the corona).
Nevertheless, if this zone is in hydrostatic equilibrium with the cold accretion disk, the maximum optical depth of the corona cannot exceed ~5 without any additional magnetic pressure.This upper limit is independent of the disk parameter. Higher optical depth of the warm skin is possible if the gas pressure is lowered by magnetic pressure or possibly by mass outflow. In this paper, we illustrate only the first case i.e. the non-zero value of magnetic field strength. When the ratio of magnetic pressure to the gas pressure is 100, the maximum optical depth of the warm corona is around 20, which is consistent with some observations.
We conclude that in the absence of magnetic pressure, additional dissipation in the outer layer is able to heat up the corona, but the requirement of hydrostatic balance with the disk, puts a strong limit on the coronal optical thickness. This limit is independent of the accretion disk parameters, i.e. its accretion rate and the mass of the central black hole.
In this context, the X-ray observations of optically thick (τcor> 5), warm coronae have a strong implication for the disk/corona system: either strong magnetic fields or vertical outflows are required to stabilize the system. What is more, the simple conditions discussed in this paper are the minimum requirements for the existence of the thick corona, and further modelling of the disk/corona interaction may likely impose even more stringent constraints for the existence of such a medium.
Acknowledgments
This research was conducted within the scope of the HECOLS International Associated Laboratory, supported in part by the Polish NCN grant DEC-2013/08/M/ST9/00664. AR and BC were supported by NCN grants No. 2011/03/B/ST9/03281, 2013/10/M/ST9/00729, and by Ministry of Science and Higher Education grant W30/7.PR/2013. They have received funding from the European Union Seventh Framework Program (FP7/2007-2013) under grant agreement No. 312789. This research has also received funding from PNHE in France, and from the french Research National Agency: CHAOS project ANR-12-BS05- 0009 (http://www.chaos-project.fr). J.M. and P.O.P. also acknowledge funding from CNRS/PICS.
References
- Ballantyne, D. R. 2014, MNRAS, 437, 2845 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., Ross, R. R., & Fabian, A. C. 2001, MNRAS, 327, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Bayless, A. J., Robinson, E. L., Hynes, R. I., Ashcraft, T. A., & Cornell, M. E. 2010, ApJ, 709, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Armitage, P. J., & Reynolds, C. S. 2015, ApJ, submitted [Google Scholar]
- Blaes, O. 2014, Space Sci. Rev., 183, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Blaes, O., Krolik, J. H., Hirose, S., & Shabaltas, N. 2011, ApJ, 733, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Crummy, J., Fabian, A. C., Gallo, L., & Ross, R. R. 2006, MNRAS, 365, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B., Nikołajuk, M., Różańska, A., et al. 2003, A&A, 412, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 420, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Ebisawa, K., Życki, P., Kubota, A., Mizuno, T., & Watarai, K.-Y. 2003, ApJ, 597, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Hao, H., Civano, F., et al. 2012, ApJ, 759, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Farinelli, R., & Titarchuk, L. 2011, A&A, 525, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gierliński, M., & Done, C. 2003, MNRAS, 342, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Gierliński, M., & Done, C. 2004, MNRAS, 349, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hirose, S., & Turner, N. J. 2011, ApJ, 732, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Hirose, S., Krolik, J. H., & Blaes, O. 2009, ApJ, 691, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Iaria, R., Di Salvo, T., D’Aì, A., et al. 2013, A&A, 549, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janiuk, A., Czerny, B., & Madejski, G. M. 2001, ApJ, 557, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, Y.-F., Stone, J. M., & Davis, S. W. 2014, ApJ, 784, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, C., Ward, M., Done, C., & Gelbord, J. 2012, MNRAS, 420, 1825 [NASA ADS] [CrossRef] [Google Scholar]
- Jourdain, E., Bassani, L., Bouchet, L., et al. 1992, A&A, 256, L38 [NASA ADS] [Google Scholar]
- Kubota, A., & Done, C. 2004, MNRAS, 353, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., Fiore, F., Elvis, M., Wilkes, B. J., & McDowell, J. C. 1997, ApJ, 477, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R.-L. 1983, Acta Astrophysica Sinica, 3, 113 [NASA ADS] [Google Scholar]
- Madej, J., & Różańska, A. 2000a, A&A, 356, 654 [NASA ADS] [Google Scholar]
- Madej, J., & Różańska, A. 2000b, A&A, 363, 1055 [NASA ADS] [Google Scholar]
- Magdziarz, P., Blaes, O. M., Zdziarski, A. A., Johnson, W. N., & Smith, D. A. 1998, MNRAS, 301, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Maisack, M., Johnson, W. N., Kinzer, R. L., et al. 1993, ApJ, 407, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Malizia, A., Molina, M., Bassani, L., et al. 2014, ApJ, 782, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1978, Stellar atmospheres 2nd. edn. (San Francisco: W. H. Freeman and Co.), 650 [Google Scholar]
- Miller, K. A., & Stone, J. M. 2000, ApJ, 534, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S., & Kallman, T. R. 2001, ApJ, 546, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., & De Moortel, I. 2012, Roy. Soc. London Philosoph. Trans. Ser. A, 370, 3217 [Google Scholar]
- Perola, G. C., Matt, G., Cappi, M., et al. 2002, A&A, 389, 802 [Google Scholar]
- Petrucci, P.-O., Paltani, S., Malzac, J., et al. 2013, A&A, 549, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pounds, K. A., Nandra, K., Stewart, G. C., George, I. M., & Fabian, A. C. 1990, Nature, 344, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Różańska, A. 1999, MNRAS, 308, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Różańska, A., & Czerny, B. 1996, Acta Astron., 46, 233 [NASA ADS] [Google Scholar]
- Różańska, A., Czerny, B., Życki, P. T., & Pojmański, G. 1999, MNRAS, 305, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Różańska, A., Dumont, A.-M., Czerny, B., & Collin, S. 2002, MNRAS, 332, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Schnittman, J. D., Krolik, J. H., & Noble, S. C. 2013, ApJ, 769, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Steiner, J. F., Reis, R. C., McClintock, J. E., et al. 2011, MNRAS, 416, 941 [CrossRef] [Google Scholar]
- Svensson, R., & Zdziarski, A. A. 1994, ApJ, 436, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Uzdensky, D. A. 2013, ApJ, 775, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Mushotzky, R. F., Reynolds, C. S., et al. 2014, ApJ, 785, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, R., & Fink, H. H. 1993, A&A, 274, 105 [NASA ADS] [Google Scholar]
- Wardziński, G., & Zdziarski, A. A. 2000, MNRAS, 314, 183 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., & Holt, S. S. 1982, ApJ, 257, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, H. J., Czerny, B., & Zycki, P. T. 1997, MNRAS, 286, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S. N., Cui, W., Chen, W., et al. 2000, Science, 287, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Życki, P. T., Done, C., & Smith, D. A. 2001, MNRAS, 326, 1367 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Dissipative slab corona on top of the non-dissipative atmosphere of the accretion disk. |
| In the text | |
 |
Fig. 2 Typical radiation structure of the accretion disk corona and upper disk atmosphere. The upper panel shows the assumed dissipation profile, the middle and lower panel show the resulting radiation flux and pressure profiles, respectively. |
| In the text | |
 |
Fig. 3 Temperature profiles in the disk/corona system for the various values of the parameters χ, τcor of the six fiducial models listed in Table 1. Each curve is labelled with its model reference number, corresponding to that given in Table 1. |
| In the text | |
 |
Fig. 4 Average coronal temperature vs. optical depth. The full curves show the dependence of the average coronal temperature on the total optical depth of the corona for various values of the fraction of total power dissipated in the corona, χ, as labelled. The dashed curves represent the hydrostatic equilibrium solutions providing the largest possible Thomson depth of the Compton cooled corona for a given χ and magnetic-to-gas-pressure ratio βm (see Sect. 6). Each of the dashed curves shows the track of the solutions in the kTav-τcor plane for a fixed value of βm (as labelled) when χ is varying. |
| In the text | |
 |
Fig. 5 Density profile around the disk corona transition for the six fiducial models detailed in Table 1. The curves are labelled by their model number. |
| In the text | |
 |
Fig. 6 The importance of Compton scattering over the bremsstrahlung at the base of corona as a function of τcor (Eq. (38)). Solid lines in each package are computed for various values of χ = 0.18,0.26,0.40,0.57,0.67 and 0.86. Each package is calculated for three different values of magnetic pressure: βm = 0,10 and 100. The horizontal dashed line represents the case where ΛC/ ΛB = 1, while vertical dotted lines mark values of coronal optical depth for which it happens. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


