| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201117980 | |
| Published online | 13 January 2012 | |
Sources of straylight in the post-focus imaging instrumentation of the Swedish 1-m Solar Telescope
Institute for Solar Physics, Royal Swedish Academy of Sciences, Albanova
University Center, 106 91 Stockholm, Sweden Stockholm Observatory, Dept. of Astronomy,
Stockholm University, Albanova University Center, 106 91
Stockholm, Sweden
e-mail: mats@astro.su.se
Received: 30 August 2011
Accepted: 30 September 2011
Context. Recently measured straylight point spread functions (PSFs) in Hinode/SOT make granulation contrast in observed data and synthetic magnetohydrodynamic (MHD) data consistent. Data from earthbound telescopes also need accurate correction for straylight and fixed optical aberrations.
Aims. We aim to develop a method for measuring straylight in the post-focus imaging optics of the Swedish 1-m Solar Telescope (SST).
Methods. We removed any influence from atmospheric turbulence and scattering by using an artificial target. We measured integrated straylight from three different sources in the same data: ghost images caused by reflections in the near-detector optics, PSFs corresponding to wavefront aberrations in the optics by using phase diversity, and extended scattering PSF wings of unknown origin by fitting to a number of different kernels. We performed the analysis separately in the red beam and the blue beam.
Results. Wavefront aberrations, which possibly originate in the bimorph
mirror of the adaptive optics, are responsible for a wavelength-dependent straylight of
20–30% of the intensity in the form of PSFs with 90% of the energy contained within a
radius of 0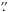 6. There are ghost images that contribute
at the most a few percent of straylight. The fraction of other sources of scattered light
from the post-focus instrumentation of the SST is only ~10-3 of the
recorded intensity. This contribution has wide wings with a FWHM ~16′′ in the blue
and ~34′′ in the red.
6. There are ghost images that contribute
at the most a few percent of straylight. The fraction of other sources of scattered light
from the post-focus instrumentation of the SST is only ~10-3 of the
recorded intensity. This contribution has wide wings with a FWHM ~16′′ in the blue
and ~34′′ in the red.
Conclusions. The present method seems to work well for separately estimating wavefront aberrations and the scattering kernel shape and fraction. Ghost images can be expected to remain at the same level for solar observations. The high-order wavefront aberrations possibly caused by the AO bimorph mirror dominate the measured straylight but are likely to change when imaging the Sun. We can therefore make no firm statements about the origin of straylight in SST data, but strongly suspect wavefront aberrations to be the dominant source.
Key words: instrumentation: miscellaneous / methods: observational / techniques: image processing / techniques: photometric / telescopes
© ESO, 2012
1. Introduction
For many years, there has been a discrepancy between the contrast in observed solar images and the corresponding images produced by magnetohydrodynamic (MHD) simulations. It was not clear whether compensation for straylight in the observations or missing physics in the simulations were at fault. This has now been resolved by measurements of the point spread function (PSF) in the Solar Optical Telescope (SOT) on the Hinode spacecraft (Wedemeyer-Böhm 2008) and comparison with artificial data (Wedemeyer-Böhm & Rouppe van der Voort 2009). Scharmer et al. (2010, see their introduction for a full account of the problem) recently initiated a project to measure the straylight sources of the Swedish 1-meter Solar Telescope (SST; Scharmer et al. 2003a) to also correct SST images for the missing contrast.
Scharmer et al. (2010) found that a significant part of the contrast reduction can be explained by high-order modes in the pupil wavefront phase that are not corrected by the Adaptive Optics (AO; Scharmer et al. 2003b) or image restorations with multi-frame blind deconvolution (MFBD; Löfdahl 2002) techniques because of the finite number of modes used in those techniques. The authors also implemented a method for correcting the contrast by means of the known statistics of atmospheric turbulence and simultaneous measurements of Fried’s parameter r0 from a wide-field wavefront sensor. However, the contrast correction they found is not sufficient to reach the contrasts expected from MHD simulations and Hinode observations.
In this paper we continue the search for the missing contrast by examining the post-focus optics of the SST. By inserting targets in the Schupmann focus, which is located close to the exit of the vacuum system, we removed all effects upstream of that point (atmosphere and telescope) and considered only error sources on the optical table. We estimated the wavefront PSF by using phase diversity (PD; Gonsalves & Chidlaw 1979; Paxman et al. 1992; Löfdahl & Scharmer 1994) and fitted the remaining straylight to a scattering PSF. In particular, we were interested in the integrated fraction of scattered light in the image data and the width of the scattering kernel.
Scattering kernels.
2. Imaging model
We model the image formation as 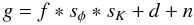 (1)where g is a flat-fielded and
dark-corrected data frame, f is the object,
sφ is the point-spread function (PSF) of
wavefront errors φ, sK is a
scattering PSF with extended wings, d represents a residual dark level that
was not subtracted properly in flat-fielding, and n is additive Gaussian
white noise. These quantities are all functions of the spatial coordinates
(x,y), suppressed when possible for compact notation. The symbol ∗
denotes convolution.
(1)where g is a flat-fielded and
dark-corrected data frame, f is the object,
sφ is the point-spread function (PSF) of
wavefront errors φ, sK is a
scattering PSF with extended wings, d represents a residual dark level that
was not subtracted properly in flat-fielding, and n is additive Gaussian
white noise. These quantities are all functions of the spatial coordinates
(x,y), suppressed when possible for compact notation. The symbol ∗
denotes convolution.
The scattering PSF, sK, is modeled as
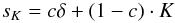 (2)where δ is the Dirac delta
function, K is a convolution kernel equal to one of
KM, KL,
KG, or KV as given in Table 1. Because it is part of the scattering PSF, we will
refer to K as a scattering kernel. Both the δ function and
the kernels are normalized in the Fourier domain by division with the value in the origin.
Owing to this normalization, (1 − c) expresses the integrated fraction of
this type of straylight.
(2)where δ is the Dirac delta
function, K is a convolution kernel equal to one of
KM, KL,
KG, or KV as given in Table 1. Because it is part of the scattering PSF, we will
refer to K as a scattering kernel. Both the δ function and
the kernels are normalized in the Fourier domain by division with the value in the origin.
Owing to this normalization, (1 − c) expresses the integrated fraction of
this type of straylight.
3. Data
The data used in this experiment were collected with the SST (Scharmer et al. 2003a) on 29 May 2010 between 17:10 and 18:40 UT.
 |
Fig. 1 Straylight target drawing. Positions (x,y) in mm, diameters (ø) in μm with tolerances of 1–2 μm. |
The primary optical system of the SST is a singlet lens with a focal length of 20.3 m at 460 nm and a 98-cm aperture. A mirror at the primary focus reflects the light to a Schupmann corrector, which forms an achromatic focus next to the primary focus. In this focal plane we placed an artificial target to isolate the optical aberrations and scattering downstream from this point. The target, manufactured by Molenaar Optics, is a 25 μm thick metal foil with six holes of different sizes, see Fig. 1. The manufacturing tolerances are very small, but close inspection of the images revealed small irregularities at the edges of the larger holes, probably caused by dust particles. Using a motor stage, we were also able insert a pinhole array used mainly for alignment purposes.
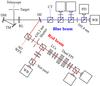 |
Fig. 2 Setup schematics. Light from the telescope enters through the target from upper left. TM = tip-tilt mirror; DM = deformable mirror; RL = reimaging lens; DC = dichrocic beamsplitter; CT = correlation tracker; WFS = wavefront sensor; LCs = Liquid Crystals; FPI = Fabry–Pérot interferometer. Only the cameras that produced images for this investigation are labeled (WB, PD). The figure is not to scale and the following intentional errors are introduced to save space: the angle to the beam reflected off the DC is drawn too wide and the transmitted and reflected beams from the first red beamsplitter are switched. |
The setup following the Schupmann focus is illustrated in Fig. 2. The beam expands (via the tip-tilt mirror) to a pupil plane at the location of the bimorph deformable mirror (DM). Here, the telescope pupil is re-imaged by a field lens located just in front of the Schupmann focus. The pupil diameter is 34 mm at this location. There is a 35 mm diameter pupil stop at the DM. This defines the pupil for pinhole images. The reimaging lens then makes a F/46 beam parallel to the optical table. The light is then split by the 500 nm dichroic beamsplitter into a blue beam and a red beam. Both beams have several cameras behind different filters. Table 2 summarizes the cameras and setup parameters used for this experiment.
Setup in the two beams.
In the blue beam one camera was nominally a “focus” camera and the other a defocused
“diversity” camera of a PD pair. These two cameras and their beamsplitter were mounted on a
common holder and could be moved together along the optical axis. This made it possible to
generate additional focus diversities without changing the relative diversity between the
wideband (WB) and PD cameras. The holder and its cameras are covered by a box that blocks
light from directions other than the beam. The relative rotation of the field in the WB and
PD cameras was measured by comparing the grid patterns of the pinhole array images. The
rotational misalignment is smaller than 0 1.
1.
In the red beam we used a single camera that was also covered by a box to block external straylight. Here, we could only add diversities by moving the camera.
The AO was running in closed loop on the central pinhole (D) of the straylight target while
the artificial target data were collected, so aberrations are assumed to be stable during
the data collection1. The telescope pointing was moving
near disk center to average out the granulation structure as well as possible. Many
exposures were collected at every position with all cameras, 3500 exposures in the blue and
10 000 in the red, for the target data as well as for dark frames and flat fields. The high
number of frames was necessary because we needed a high signal-to-noise ratio (SNR) to
measure the very faint straylight far away from the pinholes. The target data were corrected
for bias and gain variations. The corrected image
gi is calculated as 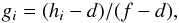 (3)where
hi is the observed data frame,
d is the average dark frame, and f is the average flat
field image. To minimize the influence from solar features in the averaged flat-field
images, the individual frames were collected while the telescope was circled over a quiet
area near disk center and the DM produced random wavefronts.
(3)where
hi is the observed data frame,
d is the average dark frame, and f is the average flat
field image. To minimize the influence from solar features in the averaged flat-field
images, the individual frames were collected while the telescope was circled over a quiet
area near disk center and the DM produced random wavefronts.
The images collected in different focus positions were not recorded simultaneously and we took steps to ensure that tiny image movements did not violate the assumption that we made in PD processing, i.e. that there is a common object in all images after summation. In a first pass, the data frames gi were co-added in their original form. In a second pass, each exposure was aligned to the summed WB image at nominal focus (WB0 image) from the first pass (separately in blue and red) with sub-pixel precision through centroiding (center of mass) on one of the holes, and a new sum was formed. By using the same image as an alignment target, both the individual images in each sum and also the sums at different focus positions were well aligned.
In the remainder of this paper we will refer to these summed images simply as the images, corresponding to g in Eq. (1). The WB0 images are shown in Fig. 3.
 |
Fig. 3 Straylight target images, WB0 in both beams, displayed with the same log scale. Left: blue beam; right: red beam. Compare Fig. 1. |
4. Straylight measurements
4.1. Ghost images
Figure 3 shows a variety of weak duplicates of the pinhole images, commonly referred to as ghost images. The most significant ghost images are shifted by only a few arcseconds and appear to be at different focus positions. These contributions must come from reflections in the beam splitters and other optics within a few cm from the detector focus, and should therefore be present during ordinary observations of the Sun as well. There are many weaker contributions that appear to be mirror images in the blue and repetitions in the different taps of the red CCD, probably originating in the camera electronics2.
The ghost images are not included in the image formation model of Eq. (1), but we can measure them here and then mask them in later processing. The strongest more or less in-focus ghosts are 1% in both the blue and red (measured on hole A).
 |
Fig. 4 PD results, the central parts of target hole F images in log scale. Top
row: observed image; center row: recreated images
M = 231; bottom row: recreated images
M = 36. The FOV shown is 2 |
4.2. Wavefront aberrations
We estimated the wavefront error PSF, sφ, through PD with the MOMFBD C++ code of van Noort et al. (2005). We processed a subfield centered on the 20 μm straylight hole F. In the blue we used 256 × 256 pixels and in the red 128 × 128 pixels, the different sizes are necessary because of the difference in image scale. The top row of Fig. 4 shows the central part of this subfield. We can see directly that the chosen focus positions were not ideal. PD0 is very similar to WB− and PD+ to WB0 in the blue, so instead of six different diversity channels, we have in reality only four. The focus is somewhere between WB0 and WB+ in the red; it is probably preferable3 to have one channel close to the focal plane, to constrain the object estimation.
Careful pre-processing is easier with point-like targets than with extended scenes, which facilitates inversions. In particular, it is possible to fine-tune the intensity bias (dark level) correction, and then make sure the total energy is the same in all focus positions. Such refined dark-level correction was performed for the purpose of PD processing. First, all images in a PD set were normalized with respect to the average intensity in the inner part of the 1 mm target hole (A). We assumed this to be the best available measure of the intensity level, insensitive to the blurring of the edge of the hole. The WB0 images, which were collected in nominal focus, we then subtracted a dark level measured as the peak (as defined by a Gaussian fit) of the histogram of image intensity within the PD processing subfield. This corrects for some of the straylight from hole A. For the data from other focus positions, we subtracted a dark level corresponding to the difference in median intensity over the entire frame (defining the dark level). Finally, the images were normalized to the same mean value, making the total energy the same in all focus positions. The dark corrections, d, in this refinement step were on the order ~10-4 of the intensity in hole A in the blue and almost ~10-3 in the red.
In the PD processing the wavefronts were expanded in atmospheric Karhunen–Loève (KL) functions, expressed as linear combinations of Zernike polynomials (Roddier 1990). These KL functions are ordered as the dominating Zernike polynomial in the notation of Noll (1976), and not by monotonically decreasing atmospheric variance. Although we were not measuring atmospheric wavefronts, we chose to use KL functions because bimorph mirrors naturally produce KL modes. We assumed that the alignment of the PD channels described in Sect. 3 is sufficient for PD processing, and accordingly did not include tilt coefficients in the fit. We defined M as the index of the highest-order mode used, i.e., we used KL modes 4–M.
In addition to the KL parametrization of the unknown wavefront, we also estimated the (Zernike) focus diversities with respect to the WB0 images, starting from the nominal values. Because the WB and PD cameras sit on a common mount and are therefore moved together, a single additional focus shift had to be determined when the three images from the PD camera were added. The diversities estimated with different M vary by no more than a few tenths of a mm and we used the values estimated with M = 210 for both M used here. The nominal and estimated diversities are shown in Table 3.
Focus diversities.
The magnitudes of the estimated diversities are all lower than their nominal values. This could be caused by a mismatch in the image formation model. We used the diameter of the ordinary telescope pupil, re-imaged on the bimorph mirror. In reality, there is diffraction in the pinhole, making the re-imaged pupil slightly fuzzy. The 7 mm defocus of the PD camera is particularly underestimated. This may be because of a mistake in the setup, so this camera was in fact defocused by less than 7 mm. These estimates confirm that the diversity setting of the PD camera was not very different from the step size of the (−, 0, +) positions.
Along with the observed images, g, in Fig. 4 we also show the recreated images, 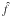 ,
based on the PD estimates
,
based on the PD estimates 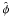 and
and 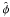 ,
for different M. An inspection of these images clearly shows that the
PSFs must be satisfactorily estimated, particularly in the blue M = 231
case.
,
for different M. An inspection of these images clearly shows that the
PSFs must be satisfactorily estimated, particularly in the blue M = 231
case.
The estimated wavefront phases without focus are shown in Fig. 5. The M = 231 estimates in the blue and red show similarities, although the red wavefronts are less well resolved than the blue wavefronts because of the smaller subfields used and possibly because of the smaller number of images with different diversities. They both have two bright rings and a dark gradient at perimeter. Both rings have brighter bumps at approximately the same positions. Particularly in the blue wavefront, the pattern resembles that of the electrodes on the bimorph mirror. The M = 36 wavefront estimates are much less resolved. Some similarities to the 231-estimates can be seen along the outer bright ring. However, with the smaller M, the KL functions apparently cannot represent the inner ring pattern visible in the M = 231 wavefront estimates.
 |
Fig. 5 Estimated wavefronts, |
The RMS values of the estimated wavefronts are listed in Table 4. The WB camera in the “0” position was out of focus by approximately 0.1 rad in the blue and 0.5 rad in the red. To make the RMS comparable between beams, we also show the rms after subtracting the best-fit focus contribution as well as calculated for a common wavelength, 500 nm. This makes the 231-estimates in red and blue agree, σ500 = 0.085 ± 0.003 waves. The 36 and 231-estimates do not agree in either beam. We are more confident in the blue 231-results because 1) the results agree between blue and red, 2) the details in the wavefront are the solution converged to when M is increased in increments from 36 to 231, and 3) the solution give estimated PSFs that recreate the observed data well, see particularly the large-diversity images in Fig. 4. The Strehl ratio4 for this solution (see Table 4) is 0.66 in the blue. Taking the two 231 solutions in red and blue together we obtain a Strehl ratio of 75 ± 2% at 500 nm after removing the focus error.
RMS and Strehl ratio of the wavefront phase.
Instrumental contributions to the wavefronts can in principle be estimated and corrected in solar data with the normal MOMFBD image restoration, except that we usually use 36 modes, far less than 231. The instrumental high-order modes are not included in the r0 measurements of the wide-field wavefront sensor so they are also not dealt with in the high-order compensation of Scharmer et al. (2010). They are therefore an independent contribution to the lowered contrast in our solar images.
In Fig. 6 we show the enclosed PSF energy as a
function of the radial coordinate. The enclosed energies for
s0 and sφ reach
90% at 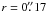 and
and
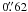 , respectively, in the blue and at
, respectively, in the blue and at
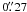 and
and
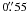 in the red.
in the red.
4.3. Extended wings
We attempted to fit a scattering PSF with extended wings to the WB0 images shown in Fig. 3. We preferred to use the 1 mm hole A, because it transmits more light than the other holes and therefore has better SNR in the far wings. To remove the pollution from the other holes and from the ghost images, we defined binary masks to be used when fitting, see Fig. 7.
For the WB0 images used for fitting the straylight model, the second-pass sums were corrected for a pattern of stripes running in the y direction. This correction was made by subtracting from all rows a smoothed version of the mean of rows 1–10. The average of this correction was ~10-4 in the blue and almost ~10-3 in the red, representing a correction of the dark level similar to the levels corrected in the previous section. (Fig. 3 shows the images after this step.) For this step the images were also normalized with respect to the average intensity in the inner part of the 1 mm hole (A).
A binary representation of hole A was generated by thresholding the WB0 image at 50% of the maximum intensity and removing contributions from the other holes. Artificial images were then made by convolving this binary image with the appropriate PSFs.
 |
Fig. 6 Enclosed energy for the diffraction-limited PSFs, s0, and for the estimated wavefront aberration PSFs, sφ. The dotted lines illustrate the radii for 90% enclosed energy. |
 |
Fig. 7 Masked straylight target images, displayed with the same log scale as in Fig. 3. Left: blue beam; right: red beam. |
 |
Fig. 8 Observed and artificial images, binary 1 mm hole convolved with s0 and sφ as measured with two different M. Left: blue beam; right: red beam. |
Figure 8 shows an azimuthal average (taking the mask
into account) of hole A, zoomed in on the hole perimeter. (The zoom makes a discrepancy in
image scale of about 1% apparent.) We show the artificial hole convolved with three
different PSFs and the observed hole. The artificial image made with PD estimated
sφ match the observed data very well in the
blue. Comparing with the diffraction limited image, it is obvious that we need to model
the wavefront PSF to isolate other sources of straylight. The match is fairly good also in
the red but the near wings are overestimated. The two PD estimated PSFs
(M = 36 and M = 231, resp.) give almost
indistinguishable results for this purpose. The straylight we will try to model with the
scattering PSF, sK, is the component that
shows up at 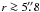 in the blue and
in the blue and
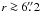 in the red.
in the red.
We now fitted Eqs. (1) and (2) to the data, using the M = 231 estimates of sφ as fixed contributions from the wavefronts. We used the Levenberg-Marquardt algorithm as implemented in the MPFIT package for IDL (Moré 1978; Markwardt 2009). In practice we fitted with two parameters c1 and c2 substituted for c and (1 − c) in Eq. (2) to allow for normalization differences in real and artificial data. We then report c = c1/(c1 + c2) as the result of the fit.
 |
Fig. 9 Fit results, angular averages of the masked images, centered on the 1 mm hole A. Beam and M as noted in the plot legends. Black: observed image; gray (in the red plots): blue observed image; brown: binary image convolved with sφ estimated with M = 231; other colors: binary image convolved with sφ as well as sK fitted with kernels as listed. |
Scattering kernel fit results.
The results of the fits are shown in Fig. 9 and in Table 5. With any of the kernels we get c > 0.99 in both beams, which appears to be a very robust result by the agreement between the different fits. In the blue we get 0.2–0.4% scattered light and in the red 0.1–0.4%.
The d parameter is returned with low values, on the order of 10-6. This indicates that the subtraction of the average top rows worked well as a dark correction refinement. Note that in the red, outside the signal-dominated radii, there is just noise, seemingly around zero. In the blue there seems to be a remaining uncorrected dark level that is not modeled by the d fit parameter. This could be caused by a geometrical asymmetry, e.g., by insufficient masking of the other holes or a dark-level gradient. It does not seem to ruin the fits.
We have less confidence in the details of the red fits than in the blue fits because the artificial image based on ŝφ overestimates the core of the PSF, see the right panel of Fig. 8. However, it is apparent from Fig. 9 that there is less straylight in the red than in the blue. Comparison of the observed red data (black in the red plots) with the observed blue data (gray) reveals a factor of ~3 difference. This would favor the lower estimate of 0.1% in the red and make the Lorentz kernel fit less believable.
In the blue the fit with a Gaussian kernel seems to fail at large radii. It also has the largest FWHM, ~20′′. The Lorentzian kernel follows the signal dominated curve better than the other kernels but the Voigt and Moffat kernels give similar results. These all have FWHM 13′′–16′′. In the red the Lorentzian kernel differs from the other kernels by giving a larger FWHM. While the Moffat kernel β is estimated with a very high value, which is compensated for by an α that is also very large, and the Voigt kernel is almost degenerated to a Gaussian, the latter three kernels agree on a FWHM of 34′′. We conclude that the Voigt and Moffat kernels, by virtue of their two fit parameters, are better able to represent the true shape of the extended wings. Using their results, we estimate the FWHM to 16′′ in the blue and 34′′ in the red.
There are noticeable residuals at 10′′ ± afewarcsec in the fits shown in Fig. 9. Particularly in the red, where this feature corresponds to 36% of the total intensity! Because of the log scale, this residual looks much lower in the blue but the corresponding error in the blue is in fact 15%. This may sound alarming but it appears this is needed to cancel fitting errors within the hole and at the hole perimeter. There are several possible reasons for the bad fits at small radii. There are small imperfections in the shape of the hole that could cause diffraction. The 50% threshold does not necessarily produce a binary representation of the hole with a correct size. The thickness of the metal foil may cause reflections in the interior walls of the hole. There are remaining variations in intensity of unknown origin within the hole. Paricularly in the red, the PD estimated sφ does not fit the core of the PSF. Owing to the truncation of the wavefront expansion, the estimated sφ may also under-represent the near wings of the PSFs. Thermal relaxation may cause variations in the sφ errors around the hole perimeter during the data collection. Despite the limited accuracy at small radii, the residuals for the extended wings at larger radii are low and we believe the kernel fits can be trusted because the 2D fitting is dominated by the larger areas where the radii are large.
5. Discussion
The wavefront aberrations are quite significant, corresponding to a Strehl ratio of ~75%. The structure of the estimated wavefronts (M = 231) with their 6- and 12-fold symmetries suggests that the bimorph mirror of the SST AO is responsible. Wavefront aberrations originating in the instrumentation will be at least partly corrected for by our standard MOMFBD image restoration. Part of the wavefront aberrations came from modes of higher order than we normally include in this processing and it is unclear how much of this would be corrected for. With the point-like object used here, the magnitude of the estimated wavefront strongly depends on the number of included modes, M. However, as shown by Scharmer et al. (2010), when the object is solar granulation, the MFBD/PD-type problem is less constrained and an estimated low-order wavefront tends to also represent the blurring caused by the higher-order modes that are not included.
The aberrations give straylight that is mostly contained in the first diffraction rings of
sφ, 90% of the energy is within a radius of
0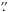 6 (see Fig. 6). The origin of this surprisingly high level of wavefront errors is unknown. One
possible source is the mounting of the 1 mm thick deformable mirror, which is clamped
between two O-rings with the tension adjusted manually by 12 screws. Another possibility is
high-order aberrations induced by a large focus error imposed on the mirror.
6 (see Fig. 6). The origin of this surprisingly high level of wavefront errors is unknown. One
possible source is the mounting of the 1 mm thick deformable mirror, which is clamped
between two O-rings with the tension adjusted manually by 12 screws. Another possibility is
high-order aberrations induced by a large focus error imposed on the mirror.
Scharmer et al. (2011, see the supporting online material) compared umbra intensity and granulation contrast in 630 nm SST data to data from SOT/Hinode and inferred a 50% straylight level with a small FWHM of less than 2′′, consistent with this straylight originating from aberrations. However, the aberrations measured here can only account for about 1/3 of the 50% straylight and would have to be stronger by a factor 2 than those measured here to fully explain the contrast in the observed granulation data.
Our best estimate of the scattering PSF, sK, is that it generates only 0.3% straylight in the blue (~397 nm) and 0.1% in the red (~630 nm). In our best fits, the FWHM of the scattering kernel K is ~16′′ in the blue and ~34′′ in the red, using the Voigt and Moffat kernels. The Gauss and Lorentz kernel fits give similar results.
It is common to truncate the wings of the scattering kernels at some radius but our fits work well without truncation, possibly because we are including the dark level d in the fit. We cannot exclude that some pollution from the holes B–F influenced the sK fits. A better straylight target should have only the 1 mm hole and the smallest hole.
After the ordinary dark-current calibrations, which consist of a subtraction of an average dark frame, the dark level was manipulated in various ways. For PD processing, we estimated and subtracted ~10-4 of the intensity in hole A from the subfield containing hole F, measured basically as the modal value within the PD processing subfield. Before the straylight kernel fitting, we also subtracted on the order of ~10-4 based on the top 10 rows of pixels. Because the kernel fitting involved a dark level, d, which was estimated to ~10-6, we can be reasonably sure that the standard dark-correction is correct to the 10-4 level. However, this is insignificant in comparison with the ghost images, the most significant of which could be measured to ~1% of the hole A intensity. Consequently, we have to allow for an additive component at the ~10-2 level, which is not modeled by the scattering kernels.
6. Conclusions
We have proposed a procedure for measuring the amount of straylight in the SST post-focus instrumentation and applied it to one wavelength in the blue beam and one wavelength in the red beam. The strength of the method is that we simultaneously measured wavefront aberrations (with phase diversity methods) and “conventional” scattered light from the same data. Thus, we were able to separate these two sources of straylight.
The dominant contributions to straylight are high-order aberrations, causing a reduction of
the Strehl ratio. The estimated Strehl ratio at 390, 500 and 630 nm is 66%, 75%, and 82%,
resp., corresponding to integrated straylight within a radius of
~0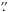 6 on the order of 34%, 25%, and 18%, resp.
The second-most important source of straylight is multiple weak, out-of-focus ghost images.
The combined effect of these is difficult to estimate but most likely contributes less than
a few percent at all wavelengths. The smallest contribution measured is from “conventional”
straylight in the form of a PSF with very wide wings (16′′ in the blue, 34′′ in the red),
this is estimated to contribute 0.3% in the blue beam and 0.1% in the red.
6 on the order of 34%, 25%, and 18%, resp.
The second-most important source of straylight is multiple weak, out-of-focus ghost images.
The combined effect of these is difficult to estimate but most likely contributes less than
a few percent at all wavelengths. The smallest contribution measured is from “conventional”
straylight in the form of a PSF with very wide wings (16′′ in the blue, 34′′ in the red),
this is estimated to contribute 0.3% in the blue beam and 0.1% in the red.
The wavefront contribution could potentially be higher when observing the Sun because of the heat that affects the mirror. Considering the small number of optical surfaces and the high optical quality of the SST telescope optics, other main contributions to the lowered contrast most likely are of atmospheric origin. This could come partly from uncorrected high-order wavefront aberrations, as discussed by Scharmer et al. (2010), and partly from scattering by dust particles in the Earth’s atmosphere.
Note added in proof
In October 2011 we were upgrading the wavefront sensor of the SST AO system. We found that switching off the mirror voltages results in a change in the science focus by approximately 9 cm along the optical axis. Due to limited electrode resolution, deformable mirrors cannot produce even low-order modes perfectly. When such a large focus has to be compensated for, there are therefore unavoidable high-order wavefront errors. We have simulated our setup and calculated the wavefront phase corresponding to the difference between a 9 cm defocus and the approximate focus produced by the mirror in order to compensate for it. The resulting RMS wavefront is 0.14 waves at 500 nm and the corresponding Strehl ratio is 0.48. This is even worse than the effects reported in Table 4 by a factor 1.6 in RMS wavefront.
We note again that these measurements (and simulations) are not directly comparable to solar observations. Nevertheless, this effect may well contribute by a significant amount to the loss of contrast in SST data. The SST optical setup will be modified to take this into account when we install our new 85-electrode deformable mirror during the summer or fall (July-Nov.) of 2012. Before that, we will also try to compensate for the effect by introducing a corresponding focus change in the Schupmann system.
Acknowledgments
We thank Vasco Henriques and Pit Sütterlin for help with the data collection. The Swedish 1-m Solar Telescope is operated on the island of La Palma by the Institute for Solar Physics of the Royal Swedish Academy of Sciences in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.
Because the target was repeatedly removed from the beam (when collecting flat fields) and inserted (when collecting target data), the mirror was alternately heated by the sunlight and allowed to cool again. Because these thermal variations cause changes in the mirror’s shape and stress, the level to which the assumption is valid is difficult to predict.
References
- Gonsalves, R. A., & Chidlaw, R. 1979, in Applications of Digital Image Processing III, ed. A. G. Tescher, Proc. SPIE, 207, 32 [Google Scholar]
- Löfdahl, M. G. 2002, in Image Reconstruction from Incomplete Data II, ed. P. J. Bones, M. A. Fiddy, & R. P. Millane, Proc. SPIE, 4792, 146 [Google Scholar]
- Löfdahl, M. G., & Scharmer, G. B. 1994, A&AS, 107, 243 [NASA ADS] [Google Scholar]
- Markwardt, C. B. 2009, in ASP Conf. Ser. 411, ed. D. A. Bohlender, D. Durand, & P. Dowler, 251 [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
- Moré, J. 1978, in Numerical Analysis, ed. G. A. Watson (Springer-Verlag), Lecture Notes in Mathematics, 630, 105 [Google Scholar]
- Noll, R. J. 1976, J. Opt. Soc. Am., 66, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Olivero, J. J., & Longbothum, R. L. 1977, J. Quant. Spectr. Rad. Transfer, 17, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Paxman, R. G., Schulz, T. J., & Fienup, J. R. 1992, J. Opt. Soc. Am. A, 9, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Roddier, N. 1990, Opt. Eng., 29, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., Bjelksjö, K., Korhonen, T. K., Lindberg, B., & Pettersson, B. 2003a, in Innovative Telescopes and Instrumentation for Solar Astrophysics, ed. S. Keil, & S. Avakyan, Proc. SPIE, 4853, 341 [Google Scholar]
- Scharmer, G. B., Dettori, P., Löfdahl, M. G., & Shand, M. 2003b, in Innovative Telescopes and Instrumentation for Solar Astrophysics, ed. S. Keil, & S. Avakyan, Proc. SPIE, 4853, 370 [Google Scholar]
- Scharmer, G. B., Löfdahl, M. G., van Werkhoven, T. I. M., & de la Cruz Rodríguez, J. 2010, A&A, 521, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Henriques, V. M. J., Kiselman, D., & de la Cruz Rodríguez, J. 2011, Science, 333, 316 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M., Rouppe van der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wedemeyer-Böhm, S. 2008, A&A, 487, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Straylight target drawing. Positions (x,y) in mm, diameters (ø) in μm with tolerances of 1–2 μm. |
| In the text | |
 |
Fig. 2 Setup schematics. Light from the telescope enters through the target from upper left. TM = tip-tilt mirror; DM = deformable mirror; RL = reimaging lens; DC = dichrocic beamsplitter; CT = correlation tracker; WFS = wavefront sensor; LCs = Liquid Crystals; FPI = Fabry–Pérot interferometer. Only the cameras that produced images for this investigation are labeled (WB, PD). The figure is not to scale and the following intentional errors are introduced to save space: the angle to the beam reflected off the DC is drawn too wide and the transmitted and reflected beams from the first red beamsplitter are switched. |
| In the text | |
 |
Fig. 3 Straylight target images, WB0 in both beams, displayed with the same log scale. Left: blue beam; right: red beam. Compare Fig. 1. |
| In the text | |
 |
Fig. 4 PD results, the central parts of target hole F images in log scale. Top
row: observed image; center row: recreated images
M = 231; bottom row: recreated images
M = 36. The FOV shown is 2 |
| In the text | |
 |
Fig. 5 Estimated wavefronts, |
| In the text | |
 |
Fig. 6 Enclosed energy for the diffraction-limited PSFs, s0, and for the estimated wavefront aberration PSFs, sφ. The dotted lines illustrate the radii for 90% enclosed energy. |
| In the text | |
 |
Fig. 7 Masked straylight target images, displayed with the same log scale as in Fig. 3. Left: blue beam; right: red beam. |
| In the text | |
 |
Fig. 8 Observed and artificial images, binary 1 mm hole convolved with s0 and sφ as measured with two different M. Left: blue beam; right: red beam. |
| In the text | |
 |
Fig. 9 Fit results, angular averages of the masked images, centered on the 1 mm hole A. Beam and M as noted in the plot legends. Black: observed image; gray (in the red plots): blue observed image; brown: binary image convolved with sφ estimated with M = 231; other colors: binary image convolved with sφ as well as sK fitted with kernels as listed. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


