© ESO, 2011

1. Introduction

Clusters of galaxies are permeated by an optically thin ionized plasma at a temperature of  ~10⁸ K. This hot intracluster medium (ICM) is composed primarily of hydrogen and helium ions, with a small fraction (<1%) of heavier elements, such as iron. A commonly adopted assumption is that helium and other heavy elements are uniformly distributed throughout the ICM, but theoretical studies initiated by Fabian & Pringle (1977), Rephaeli (1978) and Abramopoulos et al. (1981) suggest that diffusion processes will result in enrichment of iron and other heavy elements in the cluster core. Furthermore, Gilfanov & Sunyaev (1984), Qin & Wu (2000), Chuzhoy & Nusser (2003) and Chuzhoy & Loeb (2004) have shown that the diffusion speed is greater for lighter elements, and conclude that the diffusion of helium ions into the core of galaxy clusters – helium sedimentation – can occur within a Hubble time. However the problem of helium sedimentation in galaxy clusters is still under debate. Recent theoretical studies show that the presence of thermal diffusion (Shtykovskiy & Gilfanov 2010) and strong magnetic fields (Peng & Nagai 2009) in the ICM may suppress sedimentation of helium ions into the core of clusters.

The diagnostics of abundance profiles in the intracluster plasma are based primarily on line emission from heavy elements. Since helium is fully ionized in clusters and produces no lines in the X-ray energy band, its radial distribution and abundance cannot be constrained by X-ray spectroscopic data alone. X-ray observations combined with observations of the Sunyaev-Zel’dovich effect (SZE) may be used to infer the helium abundance in the ICM (Markevitch 2007); however, the limited resolution and sensitivity of current SZE interferometers have so far not enabled the measurement of the distribution of helium, even in the cluster cores where the sedimentation effect is the strongest. New capabilities for high angular resolution, high sensitivity SZE observations are currently being developed (e.g. at the Combined Array for Research in Millimeter-wave Astronomy, CARMA) which will allow observational constraints to be placed on helium sedimentation in cluster cores.

The sedimentation of helium ions within clusters of galaxies may affect the physical quantities derived from X-ray observations such as cluster gas mass, total mass (Qin & Wu 2000; Ettori & Fabian 2006), and the cosmological parameters derived from these quantities (Markevitch 2007; Peng & Nagai 2009). Using high signal to noise Chandra observations of eight relaxed galaxy clusters, we investigate a theoretical upper limit to the effect of helium sedimentation on the measurement of cluster properties; in particular, we study how this impacts mass determinations and the Y_X − M_Δ scaling relations within overdensities Δ = 2500 and Δ = 500. To determine the upper limit of helium sedimentation effect we use a limiting case of a helium sedimentation profile for 11-Gyr-old galaxy clusters, based on the numerical simulations provided by Peng & Nagai (2009). This work is the first application of a theoretically predicted helium sedimentation profile to Chandra observations.

This paper is organized as follows: in Sect. 2 we provide the details of our data reduction and modeling. The impact of helium sedimentation on X-ray derived gas and total mass and on the Y_X − M_Δ scaling relation is presented and discussed in Sect. 3. In Sect. 4 we provide conclusions. In all calculations we assume the cosmological parameters h = 0.73, Ω_M = 0.27 and Ω_Λ = 0.73.

2. X-ray observations and modeling

Our goal is to obtain density and temperature profiles for the gas in clusters based on Chandra X-ray imaging and spectroscopy, using a cluster model which accounts for a variable helium abundance as a function of radius. We describe below the reduction of the X-ray data, the application of the cluster model, and the measurement of cluster gas mass and total mass.

2.1. X-ray data reduction

We chose the eight galaxy clusters from the Allen et al. (2008) sample with the deepest Chandra ACIS-I observations (unfiltered integration time  ≥ 60 ks), all of which are available as Chandra archival data (see Table 1). The sample spans a range of redshift (0.15  <  z  <  0.69). As part of the data reduction procedure, we apply afterglow, bad pixel and charge transfer inefficiency corrections to the Level 1 event files using CIAO 4.1 and CALDB 4.1.1. We use the Markevitch et al. (2003) method for light curve filtering to eliminate flares in the background due to solar activity. The exposure times after filtering are given in Table 1. We follow the method described in Bulbul et al. (2010) for background subtraction.

We use the 0.7 − 7.0 keV energy band extraction of spectra and images in order to minimize the effect of calibration uncertainties at the lowest energies, and the effect of the high detector background at high energy. Spectra are extracted in concentric annuli surrounding the X-ray emission centroid. In this process X-ray point sources were excluded. An optically thin plasma emission model (APEC) is used, with temperature, abundance and normalization as free parameters in the spectroscopic fit (in XSPEC). The redshifts z and Galactic neutral hydrogen column densities N_H of the clusters are shown in Table 1. We adopt a 1% systematic uncertainty in each bin of the surface brightness and a 10% systematic uncertainty in temperature profile (Bulbul et al. 2010). The products of this reduction process are the X-ray surface brightness and temperature profiles shown in Fig. 2.

2.2. Application of cluster models to X-ray data

We start with the projected surface brightness (Birkinshaw et al. 1991; Hughes & Birkinshaw 1998): 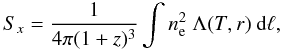${\mathit{S}}_{\mathit{x}}\mathrm{=}\frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }\mathrm{(}\mathrm{1}\mathrm{+}\mathit{z}{\mathrm{)}}^{\mathrm{3}}}\mathrm{\int }{\mathit{n}}_{\mathrm{e}}^{\mathrm{2}}\mathrm{\Lambda }\mathrm{\left(}\mathit{T,r}\mathrm{\right)}\mathrm{d}\mathit{\ell ,}$(1)where S_x is in detector units (counts s^-1 cm^-2 arcmin^-2), Λ(T,r) is the band averaged X-ray cooling function in counts cm³ s^-1, n_e is the number density of electrons, z is the redshift, and the integral is along the line of sight, ℓ.

We calculate the X-ray cooling function in two limiting cases: (i) a uniform abundance (Anders & Grevesse 1989) and (ii) the radial abundance profile of Peng & Nagai (2009) obtained for a sedimentation time scale of 11 Gyr with no magnetic field. We use the astrophysical plasma emission database (APED) which includes thermal bremsstrahlung, radiative recombination, line emission, and two-photon emission (Smith et al. 2001). In addition, we apply corrections for galactic absorption (Morrison & McCammon 1983), relativistic effects (Itoh et al. 2000), and electron-electron bremsstrahlung (Itoh et al. 2002), to obtain the X-ray emissivity (ϵ_ν) as a function of frequency ν.

The band-averaged X-ray cooling function (Λ(T,r)) is obtained by integrating the ϵ_ν over the observed Chandra energy band (0.7 − 7.0 keV): 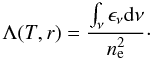$\mathrm{\Lambda }\mathrm{\left(}\mathit{T,r}\mathrm{\right)}\mathrm{=}\frac{{\mathrm{\int }}_{\mathit{\nu }}{\mathit{ϵ}}_{\mathit{\nu }}\mathrm{d}\mathit{\nu }}{{\mathit{n}}_{\mathrm{e}}^{\mathrm{2}}}\mathrm{·}$(2)The resulting band-averaged X-ray cooling function for a uniform abundance (Anders & Grevesse 1989) and a helium sedimentation profile (Peng & Nagai 2009) is shown in Fig. 1.

Fig. 1 The band-averaged X-ray cooling function, Λee(r), for two different helium distributions in the ICM: a uniform helium abundance (blue dashed line) and a helium sedimentation distribution provided by Peng & Nagai (2009) (red line). The overdensity radius r500 is the radius within which the mean cluster density is a factor of 500 times greater than the critical density of the universe at the cluster redshift.

To obtain the electron number density n_e(r) and temperature T(r) profiles, we apply the analytic model for the intracluster plasma developed by Bulbul et al. (2010) and compare the model predictions to the observed surface brightness and temperature data points found in Sect. 2.1.

Fig. 2 X-ray surface brightness (left column) and temperature profiles (right column) for the sample of eight relaxed galaxy clusters. The black points are derived from the X-ray image and spectroscopic data. The blue lines in both profiles show the best fit model to the data obtained using a uniform Anders & Grevesse (1989) helium abundance, and the red lines show the best fit model obtained using the Peng & Nagai (2009) helium sedimentation distribution; the green lines in surface brightness profiles indicate the background levels determined from the blank sky observations. The overall χ2 of the fits obtained from the uniform helium abundance and the helium sedimentation model (Tables 2 and 3) show that both distributions give equally good fits to Chandra data.

Fig. 2 Continued.

The electron number density is 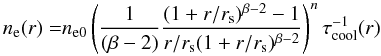$\hspace{0.17em}\begin{array}{}\begin{array}{}\end{array}{\mathit{n}}_{\mathrm{e}}\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{=}{\mathit{n}}_{\mathrm{e}\mathrm{0}}{\left(\frac{\mathrm{1}}{\mathrm{(}\mathit{\beta }\mathrm{-}\mathrm{2}\mathrm{)}}\frac{\mathrm{(}\mathrm{1}\mathrm{+}\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{s}}{\mathrm{)}}^{\mathit{\beta }\mathrm{-}\mathrm{2}}\mathrm{-}\mathrm{1}}{\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{s}}\mathrm{(}\mathrm{1}\mathrm{+}\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{s}}{\mathrm{)}}^{\mathit{\beta }\mathrm{-}\mathrm{2}}}\right)}^{\mathit{n}}{\mathit{\tau }}_{\mathrm{cool}}^{-1}\mathrm{\left(}\mathit{r}\mathrm{\right)}\begin{array}{}\end{array}\end{array}$(3)where n_e0 is the central value of the number density of electrons, r_s is the scaling radius, β + 1 is the slope of the total matter density profile, and n is the polytropic index. τ_cool(r) is the phenomenological core-taper function used for cool-core clusters (Vikhlinin et al. 2006), 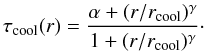${\mathit{\tau }}_{\mathrm{cool}}\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{=}\frac{\mathit{\alpha }\mathrm{+}\mathrm{(}\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{cool}}{\mathrm{)}}^{\mathit{\gamma }}}{\mathrm{1}\mathrm{+}\mathrm{(}\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{cool}}{\mathrm{)}}^{\mathit{\gamma }}}\mathrm{·}$(4)The corresponding Bulbul et al. (2010) temperature profile is 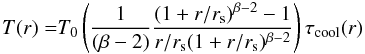$\hspace{0.17em}\begin{array}{}\begin{array}{}\end{array}\mathit{T}\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{=}{\mathit{T}}_{\mathrm{0}}\left(\frac{\mathrm{1}}{\mathrm{(}\mathit{\beta }\mathrm{-}\mathrm{2}\mathrm{)}}\frac{\mathrm{(}\mathrm{1}\mathrm{+}\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{s}}{\mathrm{)}}^{\mathit{\beta }\mathrm{-}\mathrm{2}}\mathrm{-}\mathrm{1}}{\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{s}}\mathrm{(}\mathrm{1}\mathrm{+}\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{s}}{\mathrm{)}}^{\mathit{\beta }\mathrm{-}\mathrm{2}}}\right){\mathit{\tau }}_{\mathrm{cool}}\mathrm{\left(}\mathit{r}\mathrm{\right)}\begin{array}{}\end{array}\end{array}$(5)where T₀ is the normalization parameter, and the other parameters are in common with those in Eq. (3).

We vary the model parameters using a Monte Carlo Markov Chain approach (Bonamente et al. 2004; Bulbul et al. 2010); the best fit model parameters for a uniform helium abundance and a helium sedimentation scenario are given in Table 3 and are shown by the solid blue and red curves in Fig. 2. We assume that clusters with redshift z  >  0.3 have β = 2, since the polytropic index (n) and β cannot be determined simultaneously from the data available. For all of the clusters we use a core taper parameter γ = 2.0 except for Zwicky 3146, for which we obtained a better fit with γ = 1.0. With these choices of fixed parameters, we obtain acceptable fits to the data for both the assumed uniform and sedimented helium profiles (see Tables 2 and 3).

Fig. 3 Distributions of the electron mean molecular weight (top panel) and the total mean molecular weight (bottom panel) as a function of radius for a uniform Anders & Grevesse (1989) helium abundance (blue dashed line) and for the 11 Gyr helium sedimentation model Peng & Nagai (2009)(red line).

2.3. Cluster mass

The gas mass is the volumetric integral of the number density of electrons multiplied by the electron mean molecular weight: 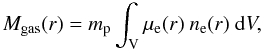${\mathit{M}}_{\mathrm{gas}}\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{=}{\mathit{m}}_{\mathrm{p}}{\mathrm{\int }}_{\mathrm{V}}{\mathit{\mu }}_{\mathrm{e}}\mathrm{\left(}\mathit{r}\mathrm{\right)}{\mathit{n}}_{\mathrm{e}}\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{d}\mathit{V,}$(6)where m_p is the proton mass and n_e(r) is defined in Eq. (3). Since the mean molecular weight of electrons μ_e(r) is dependent on the ion distribution in the plasma, we use the same approach as in the X-ray cooling function calculations to determine its radial distribution. The electron mean molecular weight μ_e(r), which is calculated for a uniform helium abundance (Anders & Grevesse 1989) and the radial helium abundance profile of (Peng & Nagai 2009) obtained for a sedimentation timescale of 11 Gyr with no magnetic field, is shown in the top panel of Fig. 3.

Similarly, the total mass is the volumetric integral of the total matter density ρ_tot(r), 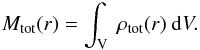${\mathit{M}}_{\mathrm{tot}}\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{=}{\mathrm{\int }}_{\mathrm{V}}{\mathit{\rho }}_{\mathrm{tot}}\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{d}\mathit{V}\mathit{.}$(7)As in Bulbul et al. (2010), the total matter density is found by ${\mathit{\rho }}_{\mathrm{tot}}\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{=}\left[\frac{{\mathit{T}}_{\mathrm{0}}\mathit{k}\mathrm{(}\mathit{n}\mathrm{+}\mathrm{1}\mathrm{)}\mathrm{(}\mathit{\beta }\mathrm{-}\mathrm{1}\mathrm{)}}{\mathrm{4}\mathit{\pi G}{\mathit{m}}_{\mathrm{p}}{\mathit{r}}_{\mathrm{s}}^{\mathrm{2}}}\right]\frac{\mathrm{1}}{{\mathit{\mu }}_{\mathrm{tot}}\mathrm{\left(}\mathit{r}\mathrm{\right)}}\frac{\mathrm{1}}{\mathrm{(}\mathrm{1}\mathrm{+}\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{s}}\mathrm{)}\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{s}}}$(8)where k is the Boltzmann constant, G is Newton’s gravitational constant, and μ_tot(r) is the total mean molecular weight, which is also dependent on the ion distribution in the plasma. The total mean molecular weight, μ_tot(r) is calculated assuming a uniform helium distribution and the helium sedimentation model (see Fig. 3 bottom panel) as was done for the μ_e calculations.

Fig. 4 The fractional change in gas mass and total mass with radius as a result of an extreme helium sedimentation with respect to masses produced by a uniform Anders & Grevesse (1989) helium abundance for a sample of eight relaxed clusters. The black lines correspond to the mean fractional change and the shaded are indicates the standard deviation of the fractional change in gas mass and total mass measurements.

3. Results

We measure cluster masses and scaling relations assuming the limiting cases of uniform helium abundance (Anders & Grevesse 1989) and the radially-varying, sedimented helium abundance profile of Peng & Nagai (2009) described in Sect. 2.2.

In order to determine the fractional change in cluster mass measurements introduced by the spatial variation in the helium distribution, we calculate gas mass and total mass for each helium abundance model. Gas mass is calculated using Eq. (6) and the electron mean molecular weight distributions shown in the top panel of Fig. 3. The total mass is calculated using Eq. (7) and the total mean molecular weight distributions shown in the bottom panel of Fig. 3. The gas mass and total mass at r₂₅₀₀ and r₅₀₀ are given in Tables 4 and 5 for both the uniform helium abundance and the sedimented case.

The fractional change with radius in gas mass and total mass measurements as a result of an extreme helium sedimentation case is shown in Fig. 4 for each of the relaxed galaxy clusters in our sample. The black line shows the mean fractional change in gas mass (left panel) and total mass (right panel). The shaded areas indicate the standard deviations of the gas mass and total mass inferred for the sample. In Table 6 we show the weighted mean percentage difference with rms errors in gas mass and total mass measurements within small cluster radius (r < 0.1   r₅₀₀), intermediate radius (r < r₂₅₀₀) and large radius (r < r₅₀₀). On average, at large radii (r < r₅₀₀) the effect of helium sedimentation on gas mass is negligible (1.3  ±  1.2%). The helium sedimentation model produces an average of 10.2  ±  5.5% decrease in the inferred total mass within r₅₀₀. Significantly stronger effects in the gas mass (10.5  ±  0.8%) and total mass (25.1  ±  1.1%) are seen at small cluster radii (r < 0.1   r₅₀₀) where the helium abundance enhancement and gradient are greater. This result is in agreement with the expected change in the mass measurements predicted by theoretical studies (Qin & Wu 2000; Peng & Nagai 2009).

3.1. Y_X – M Scaling Relation

We examine the effect of helium sedimentation on the cluster mass scaling relations. The X-ray mass proxy, Y_X, is defined as (Kravtsov et al. 2006), 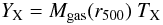${\mathit{Y}}_{\mathrm{X}}\mathrm{=}{\mathit{M}}_{\mathrm{gas}}\mathrm{\left(}{\mathit{r}}_{\mathrm{500}}\mathrm{\right)}{\mathit{T}}_{\mathrm{X}}$(9)where T_X is the mean X-ray spectroscopic temperature measured within r₅₀₀ (Kravtsov et al. 2006; Vikhlinin et al. 2009). The importance of this quantity is that there is a correlation between Y_X and the total cluster mass, M₅₀₀ (Kravtsov et al. 2006; Vikhlinin et al. 2009) and this correlation motivates Y_X as a proxy for total mass (Vikhlinin et al. 2009; Andersson et al. 2010). In this section we investigate the effect of helium sedimentation on the Y_X − M_Δ scaling relation at overdensities Δ = (2500,500) (i.e. for properties computed within r < (r₂₅₀₀,r₅₀₀)).

The Y_X − M₅₀₀ scaling relation is found using gas mass and total mass measurements shown in Tables 4 and 5 for a uniform helium abundance and helium sedimentation distributions. The average spectral temperature T_X is obtained with a single-temperature thermal plasma model (APEC) fit to the Chandra spectrum in the radial range 0.15   r₅₀₀ < r < r₅₀₀. Using the XSPEC analysis package to vary the helium abundance assumed in our spectroscopic fits, we determine that the assumed helium distribution has a negligible effect ( ≲ 1%) on the measurements of the average X-ray spectral temperatures T_X. We report the average X-ray temperature T_X and the X-ray mass proxy Y_X for a uniform helium distribution and helium sedimentation model in Table 7.

Fig. 5 The YX − M500 and YX − M2500 scaling relations for a sample of eight relaxed galaxy clusters. The blue data points and curves correspond to the measurements obtained from a uniform helium abundance case and red data points and curves correspond to the measurements obtained from a helium sedimentation model. The dashed lines show the best fit power law relation and solid curves show the 90% confidence levels.

The Y_X − M₅₀₀ scaling relation for our sample of eight relaxed galaxy clusters is shown in Fig. 5 (left panel). For each Δ, we fit the Y_X − M_Δ data using a power law relation (Vikhlinin et al. 2009), 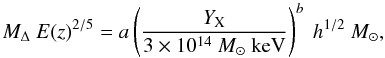$\hspace{0.17em}\begin{array}{}\begin{array}{}\end{array}{\mathit{M}}_{\mathrm{\Delta }}\mathit{E}\mathrm{(}\mathit{z}{\mathrm{)}}^{\mathrm{2}\mathit{/}\mathrm{5}}\mathrm{=}\mathit{a}{\left(\frac{{\mathit{Y}}_{\mathrm{X}}}{\mathrm{3}\mathrm{\times }{\mathrm{10}}^{\mathrm{14}} {\mathit{M}}_{\mathrm{\odot }} \mathrm{keV}}\right)}^{\mathit{b}} {\mathit{h}}^{\mathrm{1}\mathit{/}\mathrm{2}} {\mathit{M}}_{\mathrm{\odot }}\mathit{,}\end{array}$(10)where a is the normalization, b is the slope, and E(z) is the evolution function. The best fit normalizations and slopes are reported in Table 8 with the goodness of the fit. In Fig. 5 the dashed lines shows the best fit power law model and solid lines shows the 90% confidence intervals for both a uniform helium abundance and the helium sedimentation cases.

From the Y_X − M₅₀₀ fit to the data on the eight galaxy clusters in our sample, we conclude that both the uniform and sedimented helium fits are statistically consistent with the power law slope found by Vikhlinin et al. (2009) (see Table 8). Helium sedimentation changes the normalization by 10  ±  0.9% at r₅₀₀. The difference in best-fit slope between the uniform and helium sedimentation models is small compared to the statistical uncertainty.

We also investigate the effect of helium sedimentation on the Y_X − M₂₅₀₀ scaling relation. Figure 5 (right panel) shows the Y_X − M₂₅₀₀ scaling relation for our sample. We fit the Y_X − M₂₅₀₀ scaling relation data with a power law shown in Eq. (10). The dashed lines show the best fit power law relation with the goodness of fit reported in Table 9 for the uniform and sedimented helium profiles. In Fig. 5 the best fit power law model is shown in dashed line and 90% confidence levels are shown in solid lines for both uniform helium abundance and helium sedimentation models.

The self-similar Y_X − M₂₅₀₀ scaling relation discussed by Bonamente et al. (2008) is of the form: 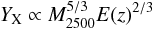${\mathit{Y}}_{\mathrm{X}}\mathrm{\propto }{\mathit{M}}_{\mathrm{2500}}^{\mathrm{5}\mathit{/}\mathrm{3}}\mathit{E}\mathrm{(}\mathit{z}{\mathrm{)}}^{\mathrm{2}\mathit{/}\mathrm{3}}$(11)which is equivalent to the Y_X − M₂₅₀₀ scaling relation form we use for this work 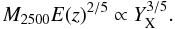${\mathit{M}}_{\mathrm{2500}}\mathit{E}\mathrm{(}\mathit{z}{\mathrm{)}}^{\mathrm{2}\mathit{/}\mathrm{5}}\mathrm{\propto }{\mathit{Y}}_{\mathrm{X}}^{\mathrm{3}\mathit{/}\mathrm{5}}\mathit{.}$(12)Recently, Bonamente et al. (2008) measured the Y_X − M₂₅₀₀ scaling relation, and found it to be consistent with the self-similar prediction, b = 1.66  ±  0.20 in Eq. (10). In our fit Y_X − M₂₅₀₀ (shown in Table 9), we also find that both the uniform helium abundance and the helium sedimentation cases are consistent with the slope measured by Bonamente et al. (2008) and with the self-similar expectation (Eq. (12)). The difference in best-fit slopes b is negligible compared to the statistical uncertainty reported in Table 9. However, we find that helium sedimentation affects the normalization of the Y_X − M₂₅₀₀ scaling relation by 13  ±  0.6%.

4. Conclusion

In this paper we investigate the upper limits to the effect of the helium sedimentation on X-ray derived cluster masses and the Y_X − M₅₀₀ and Y_X − M₂₅₀₀ scaling relations using Chandra X-ray observations of eight relaxed galaxy clusters. We used a limiting helium sedimentation profile for 11 Gyr old clusters based on the simulations performed by Peng & Nagai (2009) and compare these results with those assuming a uniform helium distribution in order to determine the maximum impact of helium sedimentation. This work is the first application of a theoretically predicted helium sedimentation profile to Chandra observations. We fit the deep exposure Chandra X-ray spectroscopic and imaging data of the eight relaxed galaxy clusters with an analytic model of the intracluster plasma developed by Bulbul et al. (2010). We demonstrated that both a uniform helium and a limiting helium sedimentation model can accurately describe the surface brightness and temperature profiles obtained from the Chandra X-ray data.

We have found that, on average, the effect of helium sedimentation on gas mass inferred within large radii (r < r₅₀₀) is negligible (1.3  ±  1.2%). The helium sedimentation model produces a 10.2  ±  5.5% mean decrease in the total mass inferred within r < r₅₀₀. Significantly stronger effects in the gas mass (10.5  ±  0.8%) and total mass (25.1  ±  1.1%) are seen at small radii owing to a larger variance in helium abundance in the inner region, r ≤ 0.1   r₅₀₀. This study supports the view that helium sedimentation should have a negligible impact on cluster mass inferred within large radii. This result is consistent with the predictions of the previous theoretical studies by Ettori & Fabian (2006) and Peng & Nagai (2009).

The fractional change in both the gas mass and the total mass measurements due to helium sedimentation do not show any trend with redshift. The strongest effect on the cluster total mass is observed on an intermediate redshift cluster, Zwicky 3146, while the smallest effect is observed on the highest redshift cluster in the sample, MACS J0744.9+3827.

In order to investigate the effect of helium sedimentation on the best-fit slopes and normalizations of the Y_X − M₅₀₀ and Y_X − M₂₅₀₀ scaling relations, we used gas mass measurements, and the mean X-ray spectroscopic temperature T_X to estimate the X-ray mass proxy Y_X for both the uniform and sedimented helium abundance profiles. Both uniform and helium sedimentation models produce slopes which are statistically consistent with the power law slopes found by Bonamente et al. (2008) and Vikhlinin et al. (2009). We have found that helium sedimentation has a negligible effect on the slopes of Y_X − M₅₀₀ and Y_X − M₂₅₀₀ scaling relations. We have also found that helium sedimentation changes the normalization of the Y_X − M₅₀₀ scaling relation by 10  ±  0.9% and the Y_X − M₂₅₀₀ scaling relation by 13  ±  0.6%.

Acknowledgments

The authors would like to thank Daisuke Nagai and the anonymous referee for comments to improve the manuscript.

References

All Tables

All Figures

Fig. 1 The band-averaged X-ray cooling function, Λee(r), for two different helium distributions in the ICM: a uniform helium abundance (blue dashed line) and a helium sedimentation distribution provided by Peng & Nagai (2009) (red line). The overdensity radius r500 is the radius within which the mean cluster density is a factor of 500 times greater than the critical density of the universe at the cluster redshift.

In the text

Fig. 2 X-ray surface brightness (left column) and temperature profiles (right column) for the sample of eight relaxed galaxy clusters. The black points are derived from the X-ray image and spectroscopic data. The blue lines in both profiles show the best fit model to the data obtained using a uniform Anders & Grevesse (1989) helium abundance, and the red lines show the best fit model obtained using the Peng & Nagai (2009) helium sedimentation distribution; the green lines in surface brightness profiles indicate the background levels determined from the blank sky observations. The overall χ2 of the fits obtained from the uniform helium abundance and the helium sedimentation model (Tables 2 and 3) show that both distributions give equally good fits to Chandra data.

In the text

	Fig. 2 Continued.
In the text

	Fig. 3 Distributions of the electron mean molecular weight (top panel) and the total mean molecular weight (bottom panel) as a function of radius for a uniform Anders & Grevesse (1989) helium abundance (blue dashed line) and for the 11 Gyr helium sedimentation model Peng & Nagai (2009)(red line).
In the text

Fig. 4 The fractional change in gas mass and total mass with radius as a result of an extreme helium sedimentation with respect to masses produced by a uniform Anders & Grevesse (1989) helium abundance for a sample of eight relaxed clusters. The black lines correspond to the mean fractional change and the shaded are indicates the standard deviation of the fractional change in gas mass and total mass measurements.

In the text

Fig. 5 The YX − M500 and YX − M2500 scaling relations for a sample of eight relaxed galaxy clusters. The blue data points and curves correspond to the measurements obtained from a uniform helium abundance case and red data points and curves correspond to the measurements obtained from a helium sedimentation model. The dashed lines show the best fit power law relation and solid curves show the 90% confidence levels.

In the text