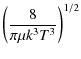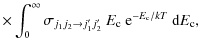EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home Home All issues Volume 517 (July 2010) A&A, 517 (2010) L2 Full HTML
Free Access
Issue
A&A
Volume 517, July 2010
Article Number L2
Number of page(s) 5
Section Letters
DOI https://doi.org/10.1051/0004-6361/201015186
Published online 30 July 2010
A&A 517, L2 (2010)

LETTER TO THE EDITOR

Astronomical identification of CN-, the smallest observed molecular anion[*],[*]

M. Agúndez1 - J. Cernicharo2 - M. Guélin3 - C. Kahane4 - E. Roueff1 - J. K\los5 - F. J. Aoiz6 - F. Lique7 - N. Marcelino2 - J. R. Goicoechea2 - M. González García8 - C. A. Gottlieb9 - M. C. McCarthy9 - P. Thaddeus9

1 - LUTH, Observatoire de Paris-Meudon, 5 Place Jules Janssen, 92190 Meudon, France
2 - Departamento de Astrofísica, Centro de Astrobiología, CSIC-INTA, Ctra. de Torrejón a Ajalvir km 4, 28850 Madrid, Spain
3 - Institut de Radioastronomie Millimétrique, 300 rue de la Piscine, 38406 Saint Martin d'Héres, France
4 - Laboratoire d'Astrophysique de l'Observatoire de Grenoble, 38041 Grenoble, France
5 - Department of Chemistry and Biochemistry, University of Maryland, College Park, MD 20742, USA
6 - Departamento de Química Física, Facultad de Química, Universidad Complutense, 28040 Madrid, Spain
7 - LOMC FRE 3102, CNRS Université du Havre, 25 rue Philippe Lebon, BP 540, 76058 Le Havre, France
8 - Instituto de Radioastronomía Milimétrica, Av Divina Pastora 7, Local 20, 18012 Granada, Spain
9 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA

Received 9 June 2010 / Accepted 5 July 2010

Abstract
We present the first astronomical detection of a diatomic negative ion, the cyanide anion CN-, and quantum mechanical calculations of the excitation of this anion by means of collisions with para-H2. The anion CN- is identified by observing the J = 2-1 and J = 3-2 rotational transitions in the C-star envelope IRC +10216 with the IRAM 30-m telescope. The U-shaped line profiles indicate that CN-, like the large anion C6H-, is formed in the outer regions of the envelope. Chemical and excitation model calculations suggest that this species forms from the reaction of large carbon anions with N atoms, rather than from the radiative attachment of an electron to CN, as is the case for large molecular anions. The unexpectedly high abundance derived for CN-, 0.25% relative to CN, indicates that its detection in other astronomical sources is likely. A parallel search for the small anion C2H- remains inconclusive, despite the previous tentative identification of the J = 1-0 rotational transition. The abundance of C2H- in IRC +10216 is found to be vanishingly small, <0.0014% relative to C2H.

Key words: astrochemistry - line: identification - molecular processes - stars: AGB and post-AGB - circumstellar matter - stars: individual: IRC +10216

1 Introduction

The molecular anions detected so far in the interstellar and circumstellar gas are all fairly heavy linear carbon chains consisting of three or more carbon atoms, and with neutral counterparts with large electron affinities: C4H-, C6H-, C8H-, C3N-, and C5N-(Cernicharo et al. 2007; Thaddeus et al. 2008; Cernicharo et al. 2008; Brünken et al. 2007a; Remijan et al. 2007; McCarthy et al. 2006). The abundance of these anions relative to the neutral counterparts increases with both size and the electron affinity of the neutral molecule, as expected for formation by radiative electron attachment (Herbst & Osamura 2008). On inspection, however, this process fails to explain the abundance of the shortest observed anions, in particular C4H- and C3N-. In IRC +10216, a carbon star envelope where both anions are found, C3N- has an anion-to-neutral abundance ratio about 50 times higher than that of C4H-, indicating that other formation processes may be at work (Thaddeus et al. 2008; Cernicharo et al. 2007; Agúndez 2009; Cordiner & Millar 2009). Studying the astronomical abundance of even shorter anions, in particular C2H- and CN-, whose formation by radiative electron attachment is very slow, should help us to answer this question.

In this Letter, we describe the identification in IRC +10216 of CN- and the results of a parallel search for C2H-. We also present quantum mechanical calculations of the collisional excitation of CN- by para-H2, using the calculated rate coefficients to model the observed lines. The chemistry of CN-in space is also briefly discussed.

2 Observations and identification of CN-

The C2H- and CN- anions are closed-shell molecules whose rotational spectrum has been recently measured in the laboratory (Amano 2008; Brünken et al. 2007b; Gottlieb et al. 2007). Their electric dipole moments are 3.1 and 0.65 Debye, respectively (Botschwina et al. 1995; Brünken et al. 2007b).

\begin{figure} \par\includegraphics[angle=0,width=7.5cm,clip]{15186fig1.eps} \end{figure} Figure 1:

Spectra of IRC +10216 covering the J = 1-0 to J = 3-2transitions of CN-. Grey horizontal boxes mark their expected positions based on the laboratory frequencies and a linewidth of 29 km s-1. Shaded areas show the fits to the line profiles obtained with the CLASS method shell. The high spectral resolution spectrum of the J = 2-1 line shows the expected position of the different hyperfine components with their relative intrinsic strengths. The intensity scale is expressed as $T_{\rm A}^*$, antenna temperature corrected for atmospheric absorption and antenna ohmic and spillover losses. To transform $T_{\rm A}^*$ into main beam brightness temperature ( $T_{\rm MB}$) in this figure and in Table 1 divide by 0.78, 0.65, and 0.44 at 112, 224, and 336 GHz, respectively.

Open with DEXTER
The present astronomical observations were carried out towards IRC +10216 with the IRAM 30-m telescope on Pico Veleta (Spain). The J = 1-0 rotational transition of CN- at 112.3 GHz was observed before 2009 in the course of a $\lambda$3 mm spectral survey (Cernicharo et al., in prep.). In IRC +10216's spectrum, this line is severely blended with a strong component of the $^2\Pi_{3/2}$ J = 81/2-79/2 transition of C6H (see Fig. 1). The J = 2-1 and J = 3-2rotational transitions of CN-, at 224.5 and 336.8 GHz, respectively, were observed between January and April 2010 with the new dual polarization EMIR receivers operating in single side-band mode. The rejection of the image side band was 13-15 dB at 224 GHz and 20-30 dB at 336 GHz, depending on the polarization, as measured with strong lines. The local oscillator was shifted in frequency to identify possible contamination from the image side band. The backends were two autocorrelators with 2 MHz and 320 kHz channel spacings, respectively. The pointing and focus of the telescope were checked every 1-2 h on both Mars and the nearby quasar OJ 287. To obtain flat baselines, the secondary mirror was wobbled by 180'' at a rate of 0.5 Hz. The zenith sky opacity at 225 GHz was typically $\sim$0.1, resulting in system temperatures of 140 K at 224 GHz and 800 K at 336 GHz. The total integration time per polarization was 3 h at 224 GHz and 9.5 h at 336 GHz, yielding a rms noise of  $T_{\rm A}^* \sim 2$ mK per 2 MHz channel at both frequencies, after averaging both polarizations.

Following our initial detection in IRC +10216 of a $T_{\rm A}^* \sim 3$ mK line at the frequency of the J = 1-0 transition of C2H- (Cernicharo et al. 2008), we searched from January to April 2010 for the J = 2-1 transition at 166.5 GHz. The line was not detected with a $T_{\rm A}^*$ rms noise level of 0.6 mK per 2 MHz channel, casting doubt on the tentative identification of the C2H- J = 1-0 line.

The CN- observed lines are shown in Fig. 1 and the derived line parameters are given in Table 1. The J = 3-2 transition of CN- is shown in the top panel of Fig. 1. It appears as a U-shaped line with the expected half width ( $v_{\rm exp} = 15\pm 1$ km s-1) that agrees in frequency to within 0.6 MHz with that of the CN-transition. The J = 2-1 transition of CN-, shown in the middle panel of Fig. 1 with a spectral resolution of 2 MHz and of 320 kHz (2.7 and 0.4 km s-1respectively), coincides with a broad spectral feature with a complex shape that is unusual for IRC +10216, since it is neither U-shaped, flat-topped, nor parabolic. It is most accurately described as a blend, as shown in Fig. 1, that can be well fitted with two components, one U-shaped with a half width $v_{\rm exp}$ of 14.5 km s-1 centered on the frequency of the J = 2-1 transition of CN- (see Table 1), the other with a parabolic profile, a half width $v_{\rm exp}$ of $15 \pm 3$ km s-1, and a rest frequency of 224  $518.3 \pm 1.5$ MHz that is close to that of the 102,9-92,8 rotational transition of SiC2 in the $\nu _3=2$ vibrational state (224 519.7 MHz; Izuha et al. 1994). Since other $\nu _3=2$ lines of SiC2 with similar intrinsic strengths have similar shapes, half widths ( $v_{\rm exp} = 8{-}15$ km s-1), and intensities ( $T_{\rm A}^* \sim 20$ mK) in our $\lambda$0.9 mm data (Kahane et al., in prep.) as our fitted parabolic component, there is little doubt that this component comes from SiC2. We note that the CN- J = 2-1 transition has several hyperfine components due to the nitrogen quadrupole, which can be grouped into three blocks lying at 224 523.9, 224 525.1, and 224 527.2 MHz, with relative line strengths of 0.27, 1, and 0.12, respectively (Gottlieb et al. 2007). Because of the severe blending with the SiC2 $\nu _3=2$ and the limited sensitivity of the astronomical observations, only the strongest hyperfine component is clearly visible in the spectrum of IRC +10216, while the middle strength component is hidden between the two stronger fitted lines (see Fig. 1), and the weakest hyperfine component lies below the noise level of the spectrum. Finally, the bottom panel of Fig. 1 shows the spectrum covering the CN- J = 1-0 transition, which is heavily blended with a strong line of C6H. The limited spectral resolution (1 MHz) and the broadening of this CN- line by the hyperfine structure (there are three components separated by 1-2 MHz; Gottlieb et al. 2007) makes it difficult to determine the relative contributions of C6H and CN- to the observed line.

Table 1:   Observed line parameters of CN-.

There are no good candidates other than CN- for the carrier of the 336 777.0 MHz line. The only plausible molecule with a transition within 2 MHz of the observed frequency, according to the line catalogs of Cernicharo, CDMS (Müller et al. 2005), and JPL (Pickett et al. 1998), is 13CCH, whose NJ,F1,F = 47/2,4,7/2-3 7/2,4,7/2 transition lies at 336 775.7 MHz. This molecule, however, is ruled out since the nearby 4 7/2,4,9/2-3 7/2,4,9/2 transition at 336 756.2 MHz, with a slightly higher intrinsic strength, is not present in our data (see Fig. 1). Since no other plausible candidate can be found for the 224 525.4 MHz line and since unidentified lines of that intensity are rare in IRC +10216 at these frequencies, we conclude that we have almost certainly detected CN-. Confirmation of this identification would be highly desirable, but may not be easy to obtain. The next two rotational transitions of CN-, at 449 and 561 GHz, cannot be observed from the ground owing to high atmospheric opacity, and still higher J transitions may be too weak to detect in a cool source such as the outer envelope of IRC +10216.

The J = 3-2 line of CN-, which appears free of contamination by background lines, has a pronounced U-shaped profile, which for a spherical expanding envelope indicates that the emission is more extended than the half-power beam of the telescope (7'' at 336 GHz). Thus, CN- appears to be confined to the same outer envelope of IRC +10216 as are other molecular anions observed in this source (e.g. Cernicharo et al. 2007; Thaddeus et al. 2008; Cernicharo et al. 2008). A column density of $5 \times 10^{12}$ cm-2 and a rotation temperature of 16 K were derived from a rotational diagram constructed with the velocity integrated intensities of the J = 2-1 and 3-2 lines given in Table 1, based on the assumption of a uniform source with a radius of 20'', which is typical of molecules distributed in the outer shell. The rotation temperature is consistent with CN- emission from the cool outer envelope. With a column density of the CN radical of $2 \times 10^{15}$ cm-2, derived from several hyperfine components of the N = 1-0 and N = 3-2 transitions, we estimate a CN-/CN abundance ratio of 0.25%, which is comparable to the C3N-/C3N ratio in this source (0.52%; Thaddeus et al. 2008).

From the upper limit to the J = 2-1 line of C2H-, we derive a 3$\sigma$ column density of < $7 \times 10^{10}$ cm-2, based on the assumption of a source with a radius of 20'' and a rotation temperature of 20 K. The estimated C2H-/C2H abundance ratio (<0.0014%) is at least 5 times lower than the already small C4H-/C4H ratio (Agúndez 2009).

3 Modeling and discussion

\begin{figure} \par\includegraphics[angle=-90,width=7.8cm,clip]{15186fig2.eps} \end{figure} Figure 2:

Abundance distribution derived for CN- in the envelope of IRC +10216 (thick grey line labeled as ``CN- fit''), as it reproduces the CN- observed line profiles (see Fig. 3). Also shown are the abundances of CN-, CN, and other molecular anions calculated with the chemical model (multiplied by 0.0003, 5, 15, 0.03, and 0.05 for CN, C2H-, C4H-, C6H-, and C5N-, respectively). The abundances are expressed as number of molecules per cubic centimeter. The angular distance is given in the top axis for an assumed distance to IRC +10216 of 120 pc.

Open with DEXTER

To obtain a more reliable estimate of the abundance and excitation conditions of CN- in IRC +10216, we carried out radiative transfer calculations based on the LVG formalism. The physical parameters of the envelope were taken from Agúndez (2009). We included the first 20 rotational levels of CN-. The rate coefficients for de-excitation by collisions with para-H2 were explicitly computed by means of quantum mechanical calculations for temperatures between 5 and 70 K and transitions involving the first 9 rotational levels of CN-. The calculations are described in Appendix A. For collisions with He, the rate coefficients computed for para-H2 were scaled down by a factor of 1.37 (the ratio of the square roots of the reduced mass of each couple of collision partners). For transitions involving rotational levels higher than J = 8, the Infinite Order Sudden approximation was used. As noted above, CN- is confined to the outer envelope of IRC +10216. We find that to reproduce the line profiles and relative intensities observed, the abundance of CN- relative to H2 must peak at a radius between 13'' and 17'' from the star. The adopted radial distribution, with a maximum abundance relative to H2 of $2.5 \times 10^{-9}$ reached at a radius of 15'' (12'' if expressed as a particle density, see grey thick line in Fig. 2), produces line profiles in reasonable agreement with the observed ones (see Fig. 3). We note that since the density decreases as the radius increases, the maximum in the particle density is reached at smaller radii than the maximum in the abundance relative to H2. The total column density across the envelope (twice the radial value) is $3 \times 10^{12}$ cm-2, in good agreement with the value derived from the rotational diagram. In the region where most of CN- is present (at a radius of $\sim$ $2\times 10^{16}$ cm, where the gas kinetic temperature is $\sim$40 K and the density of H2molecules is around $4 \times 10^4$ cm-3), the rotational levels involved in the CN- observed transitions are subthermally excited. Therefore, the collision rate coefficients utilized are found to be essential to correctly estimate the CN- abundance in the outer layers of IRC +10216's envelope.

\begin{figure} \par\includegraphics[angle=-90,width=7.8cm,clip]{15186fig3.eps} \end{figure} Figure 3:

Line profiles calculated with the LVG model (thick grey lines) using the compact CN- abundance distribution (thick grey line in Fig. 2) are compared with the observed CN- lines (black histograms). Fits to the C6H and SiC2$\nu _3=2$ lines have been subtracted in the J = 1-0 and 2-1 observed spectra. The J = 1-0 line profile is very uncertain due to the blend with the strong C6H line.

Open with DEXTER

To gain some insight into the formation of CN- in the external layers of the molecular envelope of IRC +10216, we performed chemical modeling calculations similar to those described by Cernicharo et al. (2008). The physical parameters of the envelope were taken from Agúndez (2009). The rate constants and branching ratios of the reactions of anions with H, O, and N atoms, studied in the laboratory by Eichelberger et al. (2007), were updated according to the values used by Cordiner & Millar (2009) and Walsh et al. (2009)[*]. Photodetachment rates of molecular anions were assumed by Millar et al. (2007) to depend on the electron affinity of the neutral counterpart. For CN-, we assumed the same rate expression adopted for C6H-, because the neutral counterparts of both molecules have similar electron affinities (3.862 and 3.809 eV, respectively; Rienstra-Kiracofe et al. 2002). Plotted in Fig. 2 is the calculated radial distribution of the abundances of CN- (black thin line) and some other molecular anions. CN- is predicted to form at a much greater radius than C4H-, C6H-, C3N-, and C5N-, because, unlike the other anions, it is not formed directly from the radical CN but by means of the reactions of the anions Cn-( n = 5-10) with N atoms (see also Cordiner & Millar 2009). Since CN is a small molecule, the rate constant for the reaction of radiative electron attachment is likely to be very small. Here we assumed a value of $2 \times 10^{-15}$ cm3 s-1 at 300 K, similar to that computed for C2H by Herbst & Osamura (2008). This process results in a too low formation rate for CN-, more than 5 orders of magnitude lower than that provided by the reactions of Cn-and N atoms. The reaction of HCN and H- is also a source of CN- in the inner regions of the envelope, but has only a minor contribution (less than 0.2%) to the total amount of CN-formed in the envelope. The anion C2H-, on the other hand, is solely formed by the reaction of C2H2 and H-, which takes place in the inner regions. According to our chemical model, CN- reaches a maximum abundance relative to H2 of $1.6 \times 10^{-8}$ at a radius of  $8 \times 10^{16}$ cm, and a total column density across the envelope of  $8 \times 10^{12}$ cm-2. For C2H-, the model predicts a fairly low column density of $7 \times 10^{10}$ cm-2, distributed within the innermost 1016 cm. These results agree with the recent chemical model of Cordiner & Millar (2009), who predicted that both CN-and C2H- could be detected in the circumstellar envelope of IRC +10216.

The abundance and column density predicted for CN- by the chemical model is in reasonable agreement with the value derived from the observed lines and the LVG model. However, the calculated spatial distribution differs markedly from that derived by the observations (see Fig. 2). By adopting the CN- abundance distribution obtained with the chemical model, the resulting line profiles exhibit important discrepancies from the observed ones. While the calculated absolute line intensities are about the same order of magnitude as those observed, significant disagreements between the relative intensities and the line profiles are found. The calculated line intensity decreases too rapidly when going from the J = 1-0 to the J = 3-2 line, and the computed line profiles are much too U-shaped, with nearly all the emission predicted to occur at the line edges (i.e. at the terminal expansion velocity). These discrepancies arise because the chemical model predicts that CN- is present in a region of the circumstellar envelope that is too far from the central star. An abundance distribution more compact than predicted by our chemical model may arise if the envelope is not modeled as being smooth, but as having density-enhanced shells. Cordiner & Millar (2009) recently studied the effect of these density enhancements on the radial distribution of molecular abundances and found that molecules formed in the outer envelope would concentrate at the position of the first and/or second shells, located at 15 and 27'', respectively.

The chemical model predicts C2H- to be distributed over an 8'' diameter region (see Fig. 2) with a total column density of $7 \times 10^{10}$ cm-2. Once averaged over the 14.6'' beam of the IRAM 30-m telescope at the frequency of the J = 2-1 transition, the calculated column density is about 3 times lower than, and thus consistent with, the 3$\sigma$upper limit derived from the non-detection of the J = 2-1 line.

The identification of CN- in IRC +10216 with a relatively large anion-to-neutral abundance ratio (0.25%) suggests that it may be detectable in other astronomical sources. Upper limitsto the CN-/CN abundance ratio as low as 0.2-2% were obtained in TMC-1, L1527, Barnard 1, and the Orion Bar in a previous search for the J = 2-1 transition by Agúndez et al. (2008). More sensitive observations would be needed if the abundance of CN- in other sources is similar to that found in IRC +10216.

The high abundance of CN- compared to that of C2H-demonstrates the efficiency of the reactions of N atoms and large carbon anions. A more sensitive search for C2H- might support this alternative scheme for the formation of anions in space, and perhaps explain the low observed abundance of C4H- relative to C3N-.

Acknowledgements

We acknowledge R. Chamberlin and T. G. Phillips for their kind help during a previous search of the CN- J = 3-2 transition with the Caltech Submillimeter Observatory (CSO). We are also grateful to the astronomers that helped with the observations during the 2009 winter HERA pool at the IRAM 30-m telescope, among them F. S. Tabatabaei, E. De Beck, G. Bañó, and J. Rodón. M.A. is supported by a Marie Curie Intra-European Individual Fellowship within the European Community 7th Framework Programme under grant agreement n$^{\circ}$ 235753. J.R.G. is supported by a Ramón y Cajal research contract from the Spanish MICINN and co-financed by the European Social Fund. J.K. acknowledges the partial financial supports from the University Complutense of Madrid/Grupo Santander under the program of Movilidad de Investigadores Extranjeros and from the U.S. National Science Foundation under Grant No. CHE-0848110 to M. H. Alexander. This project has been partly financed by the Spanish MICINN grants Consolider-Ingenio 2010 CSD2009-00038, AYA2009-07304, and CTQ2008-02578-BQU.

References

  1. Agúndez, M. 2009, Ph.D. Thesis, Universidad Autónoma de Madrid [Google Scholar]
  2. Agúndez, M., Cernicharo, J., Guélin, M., et al. 2008, A&A, 478, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Amano, T. 2008, J. Chem. Phys., 129, 244305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  4. Arthurs, A. M., & Dalgarno, A. 1960, Proc. R. Soc. London, Ser. A, 256, 540 [Google Scholar]
  5. Botschwina, P., Seeger, S., Mladenovic, M., et al. 1995, Int. Rev. Phys. Chem., 14, 169 [CrossRef] [Google Scholar]
  6. Boys, S. F., & Bernardi, F. 1970, Mol. Phys., 19, 553 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brünken, S., Gupta, H., Gottlieb, C. A., et al. 2007a, ApJ, 664, L43 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brünken, S., Gottlieb, C. A., Gupta, H., et al. 2007b, A&A, 464, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Cernicharo, J., Guélin, M., Agúndez, M., et al. 2007, A&A, 467, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cernicharo, J., Guélin, M., Agúndez, M., et al. 2008, ApJ, 688, L83 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cordiner, M. A., & Millar, T. J. 2009, ApJ, 697, 68 [NASA ADS] [CrossRef] [Google Scholar]
  12. Eichelberger, B., Snow, T. P., Barckholtz, C., & Bierbaum, V. M. 2007, ApJ, 667, 1283 [NASA ADS] [CrossRef] [Google Scholar]
  13. Gottlieb, C. A., Brünken, S., McCarthy, M. C., & Thaddeus, P. 2007, J. Chem. Phys., 126, 191101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Herbst, E., & Osamura, Y. 2008, ApJ, 679, 1670 [Google Scholar]
  15. Hutson, J. M., & Green, S. 1994, MOLSCAT computer code, version 14, Collaborative Computational Project No. 6 of the Science and Engineering Research Council (UK) [Google Scholar]
  16. Izuha, M., Yamamoto, S., & Saito, S. 1994, Spectrochim. Acta A, 50, 1371 [NASA ADS] [CrossRef] [Google Scholar]
  17. Knowles, P. J., Hampel, C., & Werner, H.-J. 1993, J. Chem. Phys., 99, 5219 [NASA ADS] [CrossRef] [Google Scholar]
  18. Knowles, P. J., Hampel, C., & Werner, H.-J. 2000, J. Chem. Phys., 112, 3106 [NASA ADS] [CrossRef] [Google Scholar]
  19. Lique, F., Tobo▯a, R., K▯os, J., et al. 2008, A&A, 478, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. McCarthy, M. C., Gottlieb, C. A., Gupta, H., & Thaddeus, P. 2006, ApJ, 652, L141 [NASA ADS] [CrossRef] [Google Scholar]
  21. Millar, T. J., Walsh, C., Cordiner, M. A., et al. 2007, ApJ, 662, L87 [NASA ADS] [CrossRef] [Google Scholar]
  22. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
  23. Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
  24. Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2007, ApJ, 664, L47 [NASA ADS] [CrossRef] [Google Scholar]
  25. Rienstra-Kiracofe, J. C., Tschumper, G. S., & Schaefer III, H. F. 2002, Chem. Rev., 102, 231 [CrossRef] [PubMed] [Google Scholar]
  26. Thaddeus, P., Gottlieb, C. A., Gupta, H., et al. 2008, ApJ, 677, 1132 [NASA ADS] [CrossRef] [Google Scholar]
  27. Walsh, C., Harada, N., Herbst, E., & Millar, T. J. 2009, ApJ, 700, 752 [NASA ADS] [CrossRef] [Google Scholar]
  28. Williams, H. L., Szalewicz, K., Moszynski, R., & Jeziorski, B. 1995, J. Chem. Phys., 103, 4586 [NASA ADS] [CrossRef] [Google Scholar]
  29. Woon, D. E. & Dunning, T. H. 1994, J. Chem. Phys., 100, 2975 [NASA ADS] [CrossRef] [Google Scholar]

Online Material

Appendix A: CN--H2 collision rate coefficients

The potential energy surface (PES) of the CN--H2 complex was calculated ab initio using single and double-excitation coupled cluster method with non-iterative triple excitations [CCSD(T)] (Knowles et al. 2000,1993) implemented in MOLPRO[*]. The geometry of the system was described in the body-fixed frame and characterized by three angles ($\theta$, $\theta'$, $\phi$) and the distance R between the centers of mass of H2 and CN-. The H2 bond distance was fixed at r0=1.44876a0 and the CN- bond distance was varied for the purpose of averaging the PES over the lowest vibrational state of the CN-diatom. The basis-set superposition error-correction counterpoise procedure of Boys & Bernardi (1970) was applied. The four atoms were described by the correlation-consistent triple zeta basis-set (aug-cc-pVTZ) of Woon & Dunning (1994) augmented by the (3s, 2p, 1d) midbond functions defined by Williams et al. (1995), placed at mid-distance between the CN- and H2 centers of mass. The final $V(r,R,\theta,\theta',\phi)$PES is five-dimensional, although in this work we included only three perpendicular orientations of the H2 molecule [ $(\theta',\phi)$pairs: (0,0), (0,90), (90,90)] to average over H2 rotations. In addition, the PES was averaged over the CN- internuclear distance corresponding to the CN- vibrational ground state wave function. The 2-D PES was finally obtained as an arithmetic average of three H2orientations. The full five-dimensional PES and four-dimensional scattering calculations will be presented elsewhere.

We considered collisions of CN- with para-H 2(j2=0) at low temperatures. The rotational levels of CN- and H2 are designated by j1 and j2, respectively. We used the fully quantum close-coupling approach of Arthurs & Dalgarno (1960). The standard time-independent coupled scattering equations were solved using the MOLSCAT code (Hutson & Green 1994). Calculations were carried out at values of the total energy ranging from 3.6 to 500 cm-1. The integration parameters were chosen to ensure convergence of the cross-sections over this range. At the highest total energy considered (500 cm-1), the CN- rotational basis included channels up to j1=21 to ensure convergence of the excitation functions $\sigma_{j_{1}j_{2} \to j_{1}'j_{2}'} (E_{\rm c})$ for transitions including up to the j1=8 rotational level of CN-. The rotational basis of H2 was restricted to j2=0 levels. The coupling with the j2=2 (and higher) states of H2 was not taken into account. As shown by Lique et al. (2008), this approach is expected to yield reliable results for the energy range considered here. From the above described excitation functions, one can obtain the corresponding state-resolved thermal rate coefficients by Boltzmann averaging

                  $\displaystyle k_{j_{1}j_{2} \to j_{1}'j_{2}'}(T)$ = $\displaystyle \left(\frac{8}{\pi\mu k^3 T^3}\right)^{1/2}$  
    $\displaystyle \times \int_{0}^{\infty} \sigma_{j_{1}j_{2} \to j_{1}'j_{2}'}~ E_{\rm c}~ {\rm e}^{-E_{\rm c}/kT}~ {\rm d}E_{\rm c} ,$ (1)

where k is the Boltzmann constant. To obtain precise values of the rate constants, the energy grid was chosen to be sufficiently fine to include the numerous scattering resonances. The total energy range considered in this work allows us to determine rate coefficients up to 70 K. The temperature dependence of the rate coefficients for selected de-excitation transitions is illustrated in Fig. A.1, with the values given in Table A.1.

\begin{figure} \par\includegraphics[angle=0,scale=0.475]{15186fig4.eps} \end{figure} Figure A.1:

Collisional de-excitation rate coefficients of CN- by para-H2 are shown as a function of temperature for the J = 1-0, 2-1, 2-0, and 3-1 rotational transitions of CN-.

Open with DEXTER

Table A.1:   CN--H2 collision rate coefficients (10-10cm3 s-1).

Footnotes

... anion[*]
Based on observations carried out with the IRAM 30-m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
...[*]
Appendix is only available in electronic form at http://www.aanda.org
...Walsh et al. (2009)[*]
http://www.physics.ohio-state.edu/ eric/research.html
... MOLPRO[*]
MOLPRO, version 2006.1, a package of ab initio programs, H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G. Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel and G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. Meyer and M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni and T. Thorsteinsson, see http://www.molpro.net

All Tables

Table 1:   Observed line parameters of CN-.

Table A.1:   CN--H2 collision rate coefficients (10-10cm3 s-1).

All Figures

  \begin{figure} \par\includegraphics[angle=0,width=7.5cm,clip]{15186fig1.eps} \end{figure} Figure 1:

Spectra of IRC +10216 covering the J = 1-0 to J = 3-2transitions of CN-. Grey horizontal boxes mark their expected positions based on the laboratory frequencies and a linewidth of 29 km s-1. Shaded areas show the fits to the line profiles obtained with the CLASS method shell. The high spectral resolution spectrum of the J = 2-1 line shows the expected position of the different hyperfine components with their relative intrinsic strengths. The intensity scale is expressed as $T_{\rm A}^*$, antenna temperature corrected for atmospheric absorption and antenna ohmic and spillover losses. To transform $T_{\rm A}^*$ into main beam brightness temperature ( $T_{\rm MB}$) in this figure and in Table 1 divide by 0.78, 0.65, and 0.44 at 112, 224, and 336 GHz, respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=7.8cm,clip]{15186fig2.eps} \end{figure} Figure 2:

Abundance distribution derived for CN- in the envelope of IRC +10216 (thick grey line labeled as ``CN- fit''), as it reproduces the CN- observed line profiles (see Fig. 3). Also shown are the abundances of CN-, CN, and other molecular anions calculated with the chemical model (multiplied by 0.0003, 5, 15, 0.03, and 0.05 for CN, C2H-, C4H-, C6H-, and C5N-, respectively). The abundances are expressed as number of molecules per cubic centimeter. The angular distance is given in the top axis for an assumed distance to IRC +10216 of 120 pc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=7.8cm,clip]{15186fig3.eps} \end{figure} Figure 3:

Line profiles calculated with the LVG model (thick grey lines) using the compact CN- abundance distribution (thick grey line in Fig. 2) are compared with the observed CN- lines (black histograms). Fits to the C6H and SiC2$\nu _3=2$ lines have been subtracted in the J = 1-0 and 2-1 observed spectra. The J = 1-0 line profile is very uncertain due to the blend with the strong C6H line.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=0,scale=0.475]{15186fig4.eps} \end{figure} Figure A.1:

Collisional de-excitation rate coefficients of CN- by para-H2 are shown as a function of temperature for the J = 1-0, 2-1, 2-0, and 3-1 rotational transitions of CN-.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.