| Issue |
A&A
Volume 504, Number 2, September III 2009
|
|
|---|---|---|
| Page(s) | 605 - 615 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200810097 | |
| Published online | 02 July 2009 | |
Interpreting the yield of transit surveys:
are there groups in the known transiting planets population?![[*]](/icons/foot_motif.png)
F. Fressin1 - T. Guillot1 - L. Nesta2
1 - Observatoire de la Côte d'Azur, Laboratoire Cassiopée, CNRS UMR 6202, BP 4229, 06304 Nice cedex 4, France
2 -
Observatoire Français des Conjonctures Économiques (OFCE), 250 rue Albert Einstein,
06560 Valbonne, France
Received 30 April 2008 / Accepted 24 December 2008
Abstract
Context. Each transiting planet discovered is characterized by 7 measurable quantities, that may or may not be linked. This includes those relative to the planet (mass, radius, orbital period, and equilibrium temperature) and those relative to the star (mass, radius, effective temperature, and metallicity). Correlations between planet mass and period, surface gravity and period, planet radius and star temperature have been previously observed among the 31 known transiting giant planets. Two classes of planets have been previously identified based on their Safronov number.
Aims. We use the CoRoTlux transit surveys to compare simulated events to the sample of discovered planets and test the statistical significance of these correlations. Using a model proved to be able to match the yield of OGLE transit survey, we generate a large sample of simulated detections, in which we can statistically test the different trends observed in the small sample of known transiting planets.
Methods. We first generate a stellar field with planetary companions based on radial velocity discoveries, use a planetary evolution model assuming a variable fraction of heavy elements to compute the characteristics of transit events, then apply a detection criterion that includes both statistical and red noise sources. We compare the yield of our simulated survey with the ensemble of 31 well-characterized giant transiting planets, using different statistical tools, including a multivariate logistic analysis to assess whether the simulated distribution matches the known transiting planets.
Results. Our results satisfactorily match the distribution of known transiting planet characteristics. Our multivariate analysis shows that our simulated sample and observations are consistent to 76%. The mass vs. period correlation for giant planets first observed with radial velocity holds with transiting planets. The correlation between surface gravity and period can be explained as the combined effect of the mass vs. period lower limit and by the decreasing transit probability and detection efficiency for longer periods and higher surface gravity. Our model also naturally explains other trends, like the correlation between planetary radius and stellar effective temperature. Finally, we are also able to reproduce the previously observed apparent bimodal distribution of planetary Safronov numbers in 10% of our simulated cases, although our model predicts a continuous distribution. This shows that the evidence for the existence of two groups of planets with different intrinsic properties is not statistically significant.
Key words: methods: statistical - techniques: photometric - planets and satellites: formation - planetary systems - planetary systems: formation
1 Introduction
The number of giant transiting exoplanets discovered is increasing rapidly and amounts to 32 at the date of this writing. The ability to measure the masses and radii of these objects provides us with a unique possibility to determine their composition and to test planet formation models. Although uncertainties on stellar and planetary characteristics do not allow the determination of the precise composition of planets individually, much can be learned from a global, statistical approach.
A particularly intriguing observation made by Hansen & Barman (2007) from an examination of the 18 first transiting planets is the apparent grouping of objects in two categories based on their Safronov number.
The Safronov number ![]() is defined as:
is defined as:
where
If real, this division into two groups would probably imply the existence of different formation or accretion mechanisms, or alternatively require revised evolution models.
Other puzzling observations include the possible trends between planet mass and orbital period (Gaudi et al. 2005; Mazeh et al. 2005) and between gravity and orbital period (Southworth et al. 2007, first mentioned by Noyes in 2006).
The importance of transit detections biases has been pointed out by Gaudi (2005) and Pont et al. (2006) ; they have detailed the relation between the detection criterion, the characteristics of the astrophysical targets and the observational characteristics of surveys. In a previous article (Fressin et al. 2007, hereafter Paper I), we presented CoRoTlux, a tool to statistically model a population of stars and planets and compare it to the ensemble of detected transiting planets. We showed the results to be in very good agreement with the 14 planets known at that time.
In the present article, we examine whether these trends and groups can be explained in the framework of our model or whether they imply the existence of more complex physical mechanisms for the formation or evolution of planets that are not included in present models. We first describe our model and an updated global statistical analysis of the results including 17 newly discovered planets (Sect. 2). We then examine the trends between mass, gravity and orbital period (Sect. 3), the grouping in terms of planetary radius and stellar effective temperature (Sect. 4), and the grouping in terms of Safronov number (Sect. 5).
2 Method and result update
2.1 Principle of the simulations
As described in more detail in Paper I, the generation of a population of transiting planets with CoRoTlux involves the following steps:
- 1.
- we generate a population of stars from the Besançon catalog (Robin et al. 2003);
- 2.
- Stellar companions (doubles, triples) are added using frequencies of occurrence and period distributions based on Duquennoy & Mayor (1991);
- 3.
- planetary companions with random orbital inclinations are
generated with a frequency of occurrence that depends on the host
star metallicity with the relation derived by
Santos et al. (2004). The parameters of the planets (period, mass,
eccentricity) are derived by cloning the known radial-velocity
(hereafter RV) list of planets
![[*]](/icons/foot_motif.png) . We consider only planets above
0.3 times the mass of Jupiter, which yields a list of 229 objects. This mass cut-off is chosen from radial velocity analysis
(Fischer & Valenti 2005), as their planetary occurrence relation is
considered unbiased down to this limit. Because of a strong bias of
transit surveys towards extremely short orbital periods P (less
than 2 days), we add to the list clones drawn from the
short-orbit planets found from transiting surveys. The probabilities
are adjusted so that on average
. We consider only planets above
0.3 times the mass of Jupiter, which yields a list of 229 objects. This mass cut-off is chosen from radial velocity analysis
(Fischer & Valenti 2005), as their planetary occurrence relation is
considered unbiased down to this limit. Because of a strong bias of
transit surveys towards extremely short orbital periods P (less
than 2 days), we add to the list clones drawn from the
short-orbit planets found from transiting surveys. The probabilities
are adjusted so that on average 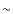 3 transit-planet clones
with
3 transit-planet clones
with 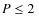 days are added to the RV list of
229 giant planets. This number is obtained by maximum likelihood
on the basis of the OGLE survey to reproduce both the planet
populations at very short periods that are not constrained by
RV measurements and the ones with longer periods that
are discovered by both types of surveys (see Paper I);
days are added to the RV list of
229 giant planets. This number is obtained by maximum likelihood
on the basis of the OGLE survey to reproduce both the planet
populations at very short periods that are not constrained by
RV measurements and the ones with longer periods that
are discovered by both types of surveys (see Paper I);
- 4.
- we compute planetary radii using a structure and evolution model
that is adjusted to fit the radius distribution of known transiting planets: the
planetary core mass is assumed to be a function of the stellar
metallicity, and the evolution is calculated by including an
extra heat source term equal to 1% of the incoming stellar heat
flux (Guillot et al. 2006; Guillot 2008)
![[*]](/icons/foot_motif.png) ;
;
- 5.
- we determine which transiting planets are detectable, given an
observational duty cycle and a level of white and red noise
estimated a posteriori (Pont et al. 2006). We also use a cut-off
in stellar effective temperature
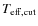 above which we
consider that it will be too difficult for RV
techniques to confirm an event. We choose
above which we
consider that it will be too difficult for RV
techniques to confirm an event. We choose
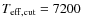 K
as a fiducial value. This value is an estimate of the limit for
K
as a fiducial value. This value is an estimate of the limit for
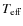 used by the OGLE follow-up group (Pont, pers. communication);
in practice it has little consequences on the results.
used by the OGLE follow-up group (Pont, pers. communication);
in practice it has little consequences on the results.
2.2 The known transiting giant planets
Table 1: Characteristics of transiting planets included in this study.
Table 2: Characteristics of stars hosting the transiting planets included in this study
Our results will be systematically compared to the sample of 31 transiting giant planets that are known at the date of this writing. These include in particular:
- 22 planets for which the refined parameters based on the uniform analysis of transit light curves and the observable properties of the host stars have been updated by Torres et al. (2008). We exclude the sub-giant Hot Neptune GJ-436 b that does not fit our mass criterion and is undetectable by current ground-based surveys.
- 9 planets recently discovered and not included in Torres et al. (2008). The characteristics of these planets have not been refined and are to be considered with more caution. Among these planets, we added the first two discoveries of the CoRoT satellite. Although CoRoT has significantly higher photometric precision and is better suited to find longer period planets than ground based surveys, we included both CoRoT-Exo-1b (Barge et al. 2008) and CoRoT-Exo-2b (Alonso et al. 2008) in our analysis, as they are the two deepest planet candidates of the initial run of the satellite and have similar periods and transit depths to planets discovered from ground-based surveys.
2.3 A new metallicity distribution for stars hosting planets
In Paper I, we had concluded that the metallicity distribution of
stars with Pegasids (planets with masses between 0.3 and
![]() and periods
P<10 days) was significantly different from those of stars with planets having longer
orbital periods. This was based on three facts:
and periods
P<10 days) was significantly different from those of stars with planets having longer
orbital periods. This was based on three facts:
- the list of radial-velocity planets known showed a lack of giant
planets with short orbital periods around metal-poor stars. Among 25 Pegasids, none were orbiting stars with
![$\rm
{\rm [Fe/H]}<-0.07$](/articles/aa/full_html/2009/35/aa10097-08/img25.png) ,
contrary to planets on longer orbits found also
around metal-poor stars;
,
contrary to planets on longer orbits found also
around metal-poor stars;
- the list of transiting planets also showed a lack of planets around metal-poor stars, with stellar metallicities ranging from -0.03 to 0.37 ( [-0.08,0.44] with error bars);
- the population of transiting planets generated with CoRoTlux
was found to systematically underpredict stellar
metallicities compared to the sample of observed transiting
planet. The period vs. metallicity diagram thus formed was found to be
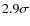 away from the maximum likelihood of the simulated planet position
in the diagram (see Paper I)
away from the maximum likelihood of the simulated planet position
in the diagram (see Paper I)![[*]](/icons/foot_motif.png) .
.
On the other hand, a similar calculation done by splitting the RV list in a low-metallicity part (
![${\rm [Fe/H]}<-0.07$](/articles/aa/full_html/2009/35/aa10097-08/img28.png) )
and a high-metallicity
part (with two different period distributions for simulated planets as a function of their host star metallicity) would end in a period vs. metallicity diagram in good agreement
with the observations (
)
and a high-metallicity
part (with two different period distributions for simulated planets as a function of their host star metallicity) would end in a period vs. metallicity diagram in good agreement
with the observations (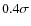 from the maximum likelihood).
from the maximum likelihood).
On the basis of an additional 51 RV giant planets and 17 transiting planets discovered since Paper I, we must now
reexamine this conclusion. Indeed, the average metallicity of stars
harboring transiting planets has evolved. The OGLE survey was
characterized by a surprisingly high value (
![]() ). The
planets discovered since have significantly lower metallicities (an
average of
). The
planets discovered since have significantly lower metallicities (an
average of
![]() ). Finally, TrES-2, TrES-3, XO-3, HAT-P-6 and
CoRoT-Exo-1 all appear to have metallicities lower than -0.07.
). Finally, TrES-2, TrES-3, XO-3, HAT-P-6 and
CoRoT-Exo-1 all appear to have metallicities lower than -0.07.
In Paper I, the metallicity distribution of simulated stars was based on that extracted from the photometric observation of the solar neighborhood of the Geneva-Copenhagen survey (Nordström et al. 2004). This metallicity distribution is in fact centred one dex lower (-0.14 instead of -0.04) than the one observed using spectrometry by RV surveys (Fischer & Valenti 2005; Santos et al. 2004). Since the latter two works are used to derive the frequency of stars bearing planets, we now choose to also use these for the metallicity distribution of stars in our fields. More specifically, our metallicity distribution law and the planet occurrence rate are obtained by combining the Santos et al. (2004) and the Fischer & Valenti (2005) surveys. Figure 1 shows the metallicity distribution and planet occurrence that result directly from these hypotheses.
As a consequence, we find that with this improved distribution of
stellar metallicities with the new sample of observed planets
alleviates the need to advocate a distinction in metallicities
between stars harboring short-period giant planets and stars that
harbor planets on longer periods. Quantitatively, our new metallicity
vs. period diagram is at
![]() of the maximum likelihood. We
therefore conclude that, contrary to Paper I, there is no
statistically significant bias between the planet periodicity and the
stellar metallicity in the observed exoplanet sample.
of the maximum likelihood. We
therefore conclude that, contrary to Paper I, there is no
statistically significant bias between the planet periodicity and the
stellar metallicity in the observed exoplanet sample.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10097fg1.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg33.png) |
Figure 1: Distribution of stars as a function of their metallicity [Fe/H]. Upper panel: fraction of stars with planets as a function of their metallicity, as obtained from radial velocity surveys (Fischer & Valenti 2005; Santos et al. 2004). Bottom panel: normalized distribution of stellar metallicities assumed in Paper I (blue) and in this work (black). The resulting [Fe/H] distribution of planet-hosting stars is also shown in red. |
| Open with DEXTER | |
2.4 Statistical evaluation of the performances of the model
As shown in detail in the appendix (see online version), the model is evaluated using univariate, two-dimensional and multivariate statistical tests. Specifically, we show that the parameters for the simulated and observed planets globally have the same mean and standard deviation and that both Student-t tests and Kolmogorov-Smirnov tests indicate that the two populations are statistically indistinguishable. However, while these univariate tests provide preliminary tests of the quality of the data, they are not sufficient because of the multiple correlations between parameters of the problem.
Table 3:
Pearson correlations between planetary and stellar characteristics.
Significant correlations (![]() 0.5) are boldfaced.
0.5) are boldfaced.
Table 3 presents the Pearson correlation coefficients between each variable. It shows that the problem indeed possesses multiple, complex correlations. In this table, the variable Y characterizes the ``reality'' of the planet considered (it is equal to 1 if the planet of the list is an observed one, and to 0 if it is a simulated planet). We see that Y is very weakly correlated with parameters of the problem. This indicates that the model is well-behaved, but does not constitute a complete validity test in itself.
Table 4 presents the results of a multivariate test using a so-called logistic regression (see the appendix for more details). This method allows us to include simultaneously all planet characteristics as predictors of the probability of being a known transiting planet (hereafter named ``real'' planets as opposed to simulated ones), thereby controlling for the correlations between all variables at once. Based on the maximum likelihood estimation method, it provides information on whether a given characteritic is positively (resp. negatively) and significantly (resp. non significantly) related to the fact of being a real planet. Moreover, it computes the probability
![]() as a general assessment of the quality of the fit. In our case, a large
as a general assessment of the quality of the fit. In our case, a large
![]() implies no significant difference between the simulated and real planets. Globally, the general fit of the model shows that simulated planets are not significantly distinct from real planets (
implies no significant difference between the simulated and real planets. Globally, the general fit of the model shows that simulated planets are not significantly distinct from real planets (
![]() ). This can be compared to a model in which model radii are artificially increased by 10%, for which
). This can be compared to a model in which model radii are artificially increased by 10%, for which
![]() (see appendix).
(see appendix).
Table 4: Logistic maximum likelihood estimates.
Table 4 also presents for each seven independent variables
of the problem plus the planet equilibrium temperature
![]() and Safronov number
and Safronov number ![]() how a given variable is correlated with the fact that a planet is ``real'' (as
opposed to being one of the simulated planets in the list). The
different statistical parameters presented in this table are defined
in the appendix. We only provide here a short
description:
how a given variable is correlated with the fact that a planet is ``real'' (as
opposed to being one of the simulated planets in the list). The
different statistical parameters presented in this table are defined
in the appendix. We only provide here a short
description: ![]() is indicative of a correlation between a
given variable and the Y (reality) variable. ``t-stat'' represent
the distance from the mean in terms of standard deviations
(student-t test).
is indicative of a correlation between a
given variable and the Y (reality) variable. ``t-stat'' represent
the distance from the mean in terms of standard deviations
(student-t test). ![]() represents the probability that the
correlation is significant. The two last parameters are evaluated
using a bootstrap method.
represents the probability that the
correlation is significant. The two last parameters are evaluated
using a bootstrap method.
The fact that the parameters ![]() in
Table 4 are non-zero indicate that there is a
correlation between each parameter and the variable Y. However,
the t-student test indicates that in every case but one (for
[Fe/H]), the values obtained for
in
Table 4 are non-zero indicate that there is a
correlation between each parameter and the variable Y. However,
the t-student test indicates that in every case but one (for
[Fe/H]), the values obtained for ![]() are consistent with 0 to within one standard deviation: the agreement between model and
observations is good. This is further shown by the high
are consistent with 0 to within one standard deviation: the agreement between model and
observations is good. This is further shown by the high ![]() values (indicative of consistency between model and observations): The
lowest
values (indicative of consistency between model and observations): The
lowest ![]() value is associated with the stellar
metallicty
value is associated with the stellar
metallicty
![]() ,
but it is high enough not to show a
statistically significant difference between our modeled sample and
real observations. However, this characteristic is the one with the
largest error bars, and the only one with missing data (for
TrES-3, TrES-4, WASP-2 and CoRoT-Exo-2). We included
,
but it is high enough not to show a
statistically significant difference between our modeled sample and
real observations. However, this characteristic is the one with the
largest error bars, and the only one with missing data (for
TrES-3, TrES-4, WASP-2 and CoRoT-Exo-2). We included
![]() ,
as it is an important feature of our model, in our multivariate
analysis, but the comparison with real planets for this
characteristic is to be considered carefully. The quality of the
agreement between observed planet characteristics and our model
improves to
,
as it is an important feature of our model, in our multivariate
analysis, but the comparison with real planets for this
characteristic is to be considered carefully. The quality of the
agreement between observed planet characteristics and our model
improves to ![]() if we remove
if we remove
![]() from our logistic
maximum likelihood estimates (see the appendix for details and
further tests).
from our logistic
maximum likelihood estimates (see the appendix for details and
further tests).
2.5 Updated mass-radius diagram
Throughout this paper, we will use density maps of the simulated
detections and compare them to the observations. These density maps
use a resolution disk template to obtain smooth plots. The size of the
resolution template is a function of the number of events present in
the diagram. The color levels follow a linear density rule for most
diagrams we show. In the case of specific diagrams showing rare long
period discoveries (more than 5 days) and large surface gravity or
Safronov number, we choose to use a logarithmic color range for
density maps to emphasize these rare events. A probability map is
established using the model detection sample (50 000 detections
obtained by simulating the number of observations from the OGLE survey) multiple times. Again, we stress that we limited our model to planets below
![]() ,
both because the question of the composition becomes more
important and complex for small planets, and because RV detection biases are also more significant ; their distribution is only partially known from RV surveys.
,
both because the question of the composition becomes more
important and complex for small planets, and because RV detection biases are also more significant ; their distribution is only partially known from RV surveys.
Figure 2 shows the mass-radius diagram density
map simulated with CoRoTlux and compared to the known planets. Gaps in
the diagram at ![]()
![]() and
and ![]()
![]() are due to the
small sample of close-in RV planets in these ranges and the fact that
our mass distribution is obtained by cloning these observed planets
rather than relying on a smooth distribution (see Paper I for a
discussion). These gaps should disappear with more discoveries
of close-in planets by RV. Otherwise, the model distribution and the
known planets are in fairly good agreement, as indicated by the
are due to the
small sample of close-in RV planets in these ranges and the fact that
our mass distribution is obtained by cloning these observed planets
rather than relying on a smooth distribution (see Paper I for a
discussion). These gaps should disappear with more discoveries
of close-in planets by RV. Otherwise, the model distribution and the
known planets are in fairly good agreement, as indicated by the
![]() distance to the maximum likelihood for this
diagram (Table 9). However, the agreement is not
as good as one would expect, probably because of two planets
with especially large radii, CoRoT-Exo-2b and TrES-4b. The
existence of these planets is a problem for evolution models in
general that goes beyond the present statistical tests that we
propose in this article.
distance to the maximum likelihood for this
diagram (Table 9). However, the agreement is not
as good as one would expect, probably because of two planets
with especially large radii, CoRoT-Exo-2b and TrES-4b. The
existence of these planets is a problem for evolution models in
general that goes beyond the present statistical tests that we
propose in this article.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg2.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg61.png) |
Figure 2:
Mass - radius relation for the transiting Pegasids discovered
to date (filled circles for planets with low Safronov number
|
| Open with DEXTER | |
3 Trends between mass, surface gravity and orbital period
3.1 A correlation between mass and orbital period of Pegasids
Figure 3 compares the known radial-velocity planets to the ones detected in transit. The figure highlights the fact that transit surveys are clearly biased towards detecting short-period planets. However, as shown in Paper I and furthermore reinforced in the present study, the two populations are perfectly compatible provided a limited proportion of very small planets (P < 2 days) is added.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg3.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg62.png) |
Figure 3: Mass-period distribution of known short-period exoplanets. Crosses correspond to non-transiting planets discovered by radial-velocity surveys. Open and filled circles correspond to transiting planets (with Safronov numbers below and over 0.05, respectively). |
| Open with DEXTER | |
Mazeh et al. (2005) had pointed out the possibility of an intriguing correlation between the masses and periods of the six first known transiting exoplanets. Figure 3 shows that the trend is confirmed with the present sample of planets. This correlation may be due to a migration rate that is inherently dependant upon planetary mass or to other formation mechanisms. It is not the purpose of this paper to analyze this correlation. However, because we use clones of the radial-velocity planets in our model, it is important to stress that this absence of small-mass planets with very short orbital distances can subtend some of the results that will be discussed hereafter.
3.2 A correlation between surface gravity and orbital period of Pegasids?
The existence of a possible anti-correlation between planetary surface
gravity
![]() and the orbital period of the
nine first transiting planets has been considered for some time
(Southworth et al. 2007). This correlation still holds
(Fig. 4) for the Pegasids with periods below 5
days and with jovian masses discovered to date. At the same
time, it is important to stress that massive objects (XO-3b,
HAT-P-2b and HD17156b) are clear outliers (see
Fig. 5): Their much larger
surface gravity probably implies that they are in a different regime.
and the orbital period of the
nine first transiting planets has been considered for some time
(Southworth et al. 2007). This correlation still holds
(Fig. 4) for the Pegasids with periods below 5
days and with jovian masses discovered to date. At the same
time, it is important to stress that massive objects (XO-3b,
HAT-P-2b and HD17156b) are clear outliers (see
Fig. 5): Their much larger
surface gravity probably implies that they are in a different regime.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg4.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg64.png) |
Figure 4: Planetary surface gravity versus orbital period of transiting giant planets discovered to date (circles) compared to a simulated joint probability density map (contours). Symbols and density plot are the same as in Fig. 2. |
| Open with DEXTER | |
Our model agrees well with the observations (in this P-g diagram real planets are at 0.51![]() from maximum likelihood
of the simulated results). We can explain the apparent correlation in
Fig. 4 as stemming from the
existence of two zones with few detectable transiting giant
planets:
from maximum likelihood
of the simulated results). We can explain the apparent correlation in
Fig. 4 as stemming from the
existence of two zones with few detectable transiting giant
planets:
- 1.
- the bottom left part of the diagram where planets are rare, because of a lack of light planets (with low surface gravity) with short periods, as discussed in Sect. 3.1;
- 2.
- the upper right part of the diagram (high surface gravity, low planetary radius) where transiting planets are less likely to transit and more difficult to detect.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg5.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg66.png) |
Figure 5: Same figure as Fig. 4 with extended surface gravity and period ranges. Note that the scale of the color levels is logarithmic, in order to emphasize the presence of outliers. |
| Open with DEXTER | |
Globally, Figs. 4 and 5 indicate that the relation between planet surface gravity and orbital period is not a consequence of a link between the planet composition and its orbital period. Rather, we see it as a consequence of the correlation between planetary mass and orbital period for short period giant planets, which is, as discussed in the previous section, probably linked to mass-dependent migration mechanisms.
4 A correlation between stellar effective temperature and planet radius ?
The range of radius of Pegasids is surprisingly large,
especially when one considers the difference in compositions (masses
of heavy elements varying from almost 0 to ![]()
![]() )
that are required to explain known transiting planets within the
same model (Guillot et al. 2006; Guillot 2008). Our underlying planet
composition/evolution model is based on the assumption of a
correlation of the stellar metallicity with the heavy element
content in the planet. We checked that no other variable is
responsible for a correlation that would affect this conclusion.
)
that are required to explain known transiting planets within the
same model (Guillot et al. 2006; Guillot 2008). Our underlying planet
composition/evolution model is based on the assumption of a
correlation of the stellar metallicity with the heavy element
content in the planet. We checked that no other variable is
responsible for a correlation that would affect this conclusion.
We present the results obtained in the
![]() diagram as they are the most interesting: the two variables indeed
are positively correlated. Furthermore, given that errors in the stellar
parameters are the main sources of uncertainty in the planetary
radius determinations, one could suppose that a systematic error in
the stellar radius measurement as a function of its effective temperature
could be the cause of the
variation in the estimated planetary radii. If true, this may
alleviate the need for extreme variations in composition. It would
cast doubts on the stellar metallicity vs. planetary heavy element
content correlation.
diagram as they are the most interesting: the two variables indeed
are positively correlated. Furthermore, given that errors in the stellar
parameters are the main sources of uncertainty in the planetary
radius determinations, one could suppose that a systematic error in
the stellar radius measurement as a function of its effective temperature
could be the cause of the
variation in the estimated planetary radii. If true, this may
alleviate the need for extreme variations in composition. It would
cast doubts on the stellar metallicity vs. planetary heavy element
content correlation.
Table 5: Mean planet radius for cool versus hot stars.
As shown in Table 5, the mean radius of
planets orbiting cool stars (
![]() K) is
K) is
![]() and it is
and it is
![]() for planets orbiting hot
stars (
for planets orbiting hot
stars (
![]() K). Slightly smaller values are obtained
in our simulation when considering all transiting
planets. However, the values obtained when considering only the detectable transiting planets are in extremely good agreement
with the observations.
K). Slightly smaller values are obtained
in our simulation when considering all transiting
planets. However, the values obtained when considering only the detectable transiting planets are in extremely good agreement
with the observations.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg6.ps}\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg77.png) |
Figure 6: Stellar effective temperature versus planetary radius of transiting giant planets discovered to date (circles) compared to a simulated joint probability density map (contours). The black line is the sliding average of radii in the [-250 K,+250 K] effective temperature interval for all simulated transiting planets (both below and over the detection threshold). The white line is the same average for the detectable planets in the simulation. The symbols and density map are the same as in Fig. 2. |
| Open with DEXTER | |
Figure 6 shows in more detail how stellar effective temperature and planetary radius are linked. We interpret the correlation between the two as the combined effect of irradiation (visible with the plotted average radius of all planets with at least one transit event in simulated light curves) and detection bias (visible with the plotted average radius of simulated planets detected):
- 1.
- the planets orbiting bright stars are more irradiated. The mean radius of a planet orbiting a warmer star is thus higher at a given period. This effect is taken into account in our planetary evolution model (see Guillot & Showman 2002; Guillot et al. 2006);
- 2.
- the detection of a planet of a given radius is easier for cooler stars since for main sequence stars effective temperature and stellar radius are positively correlated.
As in the mass-radius diagram (Fig. 2), there is an outlier at the bottom of Fig. 6, HD149026b. As discussed previously, this object lies at the boundary of what we could simulate, both in terms of masses and amounts of heavy elements, so that we do not consider this as significant. It is also presently not detectable from a transit survey. Clearly, with more sensitive transit surveys, the presence of low-mass planets with a large fraction of heavy elements compared to hydrogen and helium will populate the bottom part of this diagram.
A last secondary outcome of the study of this diagram concerns the
possible existence of two groups of planets roughly separated by a
![]() K line. We find that the existence of two such
groups separated by
K line. We find that the existence of two such
groups separated by ![]() 200 K or more appears serendipitously in
our model in 10% of the cases and is therefore
not statistically significant.
200 K or more appears serendipitously in
our model in 10% of the cases and is therefore
not statistically significant.
5 Two classes of Hot Jupiters, based on their Safronov numbers?
According to Hansen & Barman (2007), the 16 planets discovered at the time
of their study show a bimodal distribution in Safronov numbers, half
of the sample having Safronov numbers
![]() (``class I'') while the
other half is such that
(``class I'') while the
other half is such that
![]() (``class II''). They also
point out that the equilibrium temperatures of the two classes of
planets differ, the class II planets being on average hotter. This is
potentially of great interest because the Safronov number is
indicative of the efficiency with which a planet scatters other bodies
and therefore this division in two classes, if real, may tell us
something about the processes that shaped planetary systems.
(``class II''). They also
point out that the equilibrium temperatures of the two classes of
planets differ, the class II planets being on average hotter. This is
potentially of great interest because the Safronov number is
indicative of the efficiency with which a planet scatters other bodies
and therefore this division in two classes, if real, may tell us
something about the processes that shaped planetary systems.
5.1 No significant gap between two classes
Figure 7 shows how the situation has
evolved with the new transiting giant planets discovered thus far:
Although a few planets have narrowed the gap between the two
ensemble of planets, it is still present and located at a Safronov
number
![]() .
The two classes also have mean equilibrium
temperatures that differ.
.
The two classes also have mean equilibrium
temperatures that differ.
On the other hand, our model naturally predicts a continuous
distribution of Safronov numbers. A trend is found in which planets
with high equilibrium temperatures tend to have lower Safronov
numbers, which is naturally explained by the fact that equilibrium
temperature and orbital distance are directly linked (remember that
![]() )).
)).
We find that our
![]() joint probability density
function is representative of the observed population, being at
joint probability density
function is representative of the observed population, being at
![]() from the maximum likelihood (see appendix). A K-S test
on the Safronov number yields a distance between the observed and
simulated distributions of 0.163 and a corresponding probability for
a good match of 0.38, a value that should be improved in future
models, but that shows that the two ensembles are statistically
indistinguishable.
from the maximum likelihood (see appendix). A K-S test
on the Safronov number yields a distance between the observed and
simulated distributions of 0.163 and a corresponding probability for
a good match of 0.38, a value that should be improved in future
models, but that shows that the two ensembles are statistically
indistinguishable.
Figure 8 compares the histogram of the distribution of Safronov number for simulated detections with the histogram of real events. Interestingly, although distributions seem different from the 0.05-scale histogram, with a gap appearing in the 0.05-0.055 slots, they fit each other when using the 0.1-scale histogram, more appropriate for this low-number statistics analysis (7 intervals for 31 events).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg7.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg85.png) |
Figure 7: Safronov number versus equilibrium temperature of transiting giant planets discovered to date (circles) compared to a simulated joint probability density map (contours). Open (resp. filled) circles correspond to class I (resp. class II) planets. The symbols and density map are the same as in Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg8.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg86.png) |
Figure 8: Comparison of the distribution of Safronov number between simulated detections (Red) and real events (Black). Top: histogram with 6 0.1-scale columns, Bottom: histogram with 12 0.05-scale columns. |
| Open with DEXTER | |
Figure 9 shows the probability of obtaining a gap of a given size between the Safronov numbers of two potential groups of a random draw. 26 of the known transiting Pegasids have their Safronov number between 0 and 0.1. Setting a minimum number of 5 planets in each of two classes, we look for the largest gap between Safronov numbers of a random draw of 26 simulated Pegasids. For each one of the 10 000 Monte-Carlo draws among the model detections sample, we calculate how large the most important difference is between successive Safronov numbers of the 26 random draws. We find that a gap of 0.0102 between two potential groups is an uncommon event (10% of the cases, as 4% of the cases have gaps of this size, and a total of 6% of the cases have larger gaps), yet it is not exceptionally rare. Considering the 7 planet/star characteristics and their many possible combinations, this level of ``rarity'' is not statistically significant.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg9.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg87.png) |
Figure 9: Occurrence of the largest observed separation of Safronov numbers between two ``groups'' selected from random draws among the model detections sample. The vertical line shows the separation (0.0102) between the two classes of planets as inferred from the observational sample. |
| Open with DEXTER | |
It is also interesting to consider the few high-Safronov-number
planets discovered as in
Fig. 10. The different gaps in the
diagram are due to our mass vs. period reproductions of RV planets
that do not uniformly cover the space of parameters. The unpopulated part
in the right edge of the density map is due to the absence of massive
planets in the
![]() range at close orbit in the RV
planets. The simulated detections at both high Safronov number and
equilibrium temperature correspond to simulated clones of the planet
HD41004b, with its large mass of 18
range at close orbit in the RV
planets. The simulated detections at both high Safronov number and
equilibrium temperature correspond to simulated clones of the planet
HD41004b, with its large mass of 18
![]() and its very
close-in period of 1.33 days.
and its very
close-in period of 1.33 days.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097f10.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg90.png) |
Figure 10: Same as Fig. 7 but for a larger range of Safronov numbers. Note that the scale of the color levels is logarithmic, in order to emphasize the presence of outliers. |
| Open with DEXTER | |
5.2 No bimodal distribution visible in other diagrams.
When plotted as a function of different stellar (effective temperature, mass, radius) and planetary characteristics (mass, radius, period, equilibrium temperature), the two potential Safronov classes do not differ in a significant way. When plotting our simulated detections as a function of their Safronov number in different diagrams, the two groups formed by restricting our model detection sample with a Safronov number cut-off set at 0.05 partly overlap each other in most diagrams. Here, we choose to present the planetary mass vs. equilibrium temperature diagram used to provide a clear separation between the two populations (Torres et al. 2008; Hansen & Barman 2007). We present in Fig. 11 this diagram as an example of the partial overlap of the class I and class II detected planets and probability density maps. Contrary to indications based on a smaller sample of observations, there is no longer a clear separation in this diagram between class I and class II planets.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097f11.ps}\par\includegraphics[width=7.5cm,clip]{10097f12.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg91.png) |
Figure 11:
Planetary mass versus equilibrium temperature of
transiting giant planets discovered to date (circles) compared to
a simulated joint probability density map (contours). Top
panel: the density map accounts only for simulated planets
with a Safronov number
|
| Open with DEXTER | |
5.3 No correlation between metallicity and Safronov number/class.
Torres et al. (2008) showed that a significant difference could be
observed between the metallicity distributions of the two Safronov
classes. The high-Safronov number class (class I,
![]() )
had its host star metallicity centered on 0.0, and the
low-Safronov number class (class II) was centered on
0.2. They pointed out that the Safronov numbers for Class I planets
show a decreasing trend with metallicity.
)
had its host star metallicity centered on 0.0, and the
low-Safronov number class (class II) was centered on
0.2. They pointed out that the Safronov numbers for Class I planets
show a decreasing trend with metallicity.
The two recent discoveries of CoRoT-Exo-1-b (
![]() and
and
![]() )
and OGLE TR182-b (
)
and OGLE TR182-b (
![]() and
and
![]() )
tend to contradict this argument. Considering the 31 known giant planets,
the mean metallicity of stars hosting class I planets is now
)
tend to contradict this argument. Considering the 31 known giant planets,
the mean metallicity of stars hosting class I planets is now
![]() ,
and it is 1.6 for class II planets.
Figure 12 shows that although the
metallicity vs. Safronov number distribution of detections we simulate
is a likely result (
,
and it is 1.6 for class II planets.
Figure 12 shows that although the
metallicity vs. Safronov number distribution of detections we simulate
is a likely result (
![]() from maximum likelihood), the
potential anticorrelation between
from maximum likelihood), the
potential anticorrelation between ![]() and host star [Fe/H]
(pointed out by Torres et al. (2008)) for class I planets is not
present in our simulation, which shows a continouous density map.
and host star [Fe/H]
(pointed out by Torres et al. (2008)) for class I planets is not
present in our simulation, which shows a continouous density map.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097f13.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg98.png) |
Figure 12: Safronov number of transiting planets as a function of their host star metallicity. The density map with linear contours comes from the model detection sample. Open and filled circles are respectively class I planets (with Safronov number over 0.05) and class II planets (with Safronov number below 0.05) Symbols and density plot are the same as in Fig. 2. |
| Open with DEXTER | |
5.4 No significant gap between two Safronov number classes.
Our study has shown us that a separation between two groups of planets linked to their Safronov number is unlikely for at least two reasons:
- 1.
- the separation between the two groups is marginal. It only
appears in the Safronov number histogram if the resolution of the
histogram is high in comparison to the number of events sampled. The
separation of
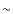 0.01 between two possible Safronov classes has
a non-negligible
0.01 between two possible Safronov classes has
a non-negligible 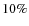 probability of occurring serendipitously in our
distribution, which is otherwise continuous. Considering the
relatively numerous parameters (4 for the star, 3 linked to the
planet) and their combinations, such a division to two groups
appears quite likely to occur fortuitously for one such parameter;
probability of occurring serendipitously in our
distribution, which is otherwise continuous. Considering the
relatively numerous parameters (4 for the star, 3 linked to the
planet) and their combinations, such a division to two groups
appears quite likely to occur fortuitously for one such parameter;
- 2.
- the separation between the two classes is not present in any
figures other than the ones involving the Safronov number
itself. This includes also the separation in metallicity vs.
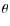 which is
not statistically significant, especially given recent discoveries
of CoRoT-Exo-1b and OGLE-TR-182b.
which is
not statistically significant, especially given recent discoveries
of CoRoT-Exo-1b and OGLE-TR-182b.
6 Conclusions
We have presented a coherent model of a population of stars and planets that matches within statistical errors the observations of transiting planets performed thus far. Thanks to new observations, we have improved on our previous model (Paper I). In particular, we now show that with slightly improved assumptions about the metallicity of stars in the solar neighborhood, the metallicity of stars with transiting giant planets can be explained without assuming any bias in period vs. metallicity.
In order to validate our model, we have used a series of univariate, bivariate and multivariate statistical tests. As the sample of radial-velocimetry planets and of transiting planets grows, we envision that with these tools we will be able to much better characterize the planet population in our Galaxy and its dependence on the star population, and also test models of planet formation and evolution.
With the current sample of transiting planets, our model provides a very good match to the observations, both when considering planetary and stellar parameters one by one or globally. Our analysis has revealed that the parameters for the modeled planets are presently statistically indistinguishable from the observations, although there may be room for improvement of the model. It should be noted that our underlying assumptions for the composition and evolution of planets and stellar populations are relatively simple. With a larger statistical sample, tests of these assumptions will be possible and will place important constraints on the planet-star distribution in our galactic neighborhood. The CoRoT mission is expected to be very important in that respect, especially given the careful determination of the characteristics of the stellar population that is being monitored.
Using this method, we have been able to analyze and explain the different correlations observed between transiting planets characteristics:
- 1.
- Mass vs. period: one of the first correlations observed
among the planet/star characteristics was the mass vs. period relation of
close-in RV planets (Mazeh et al. 2005). Although our model does not
explain it, we confirm with a sample that is now 4 times larger than
at the time of the publication reporting a lack of low-mass planets
(
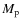
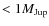 )
with very short periods (P<2 days).
)
with very short periods (P<2 days).
- 2.
- Surface gravity vs. period: there is an inverse correlation
between the surface gravity and period of transiting planets. We show
that this correlation is caused by the above mass vs. period effect,
and by a lower detection probability for planets with longer periods
and higher surface gravities.
- 3.
- Radius vs. stellar effective temperature: planets around stars with higher effective temperatures tend to have larger sizes. This is naturally
explained by a combination of slower contraction due to the larger
irradiation and by the increased difficulty in finding planets around
hotter, larger stars.
- 4.
- Safronov number: Torres et al. (2008); Hansen & Barman (2007) have
identified a separation between two classes of planets, based on
their Safrononov number, and visible in different diagrams (
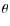 vs.
vs.
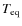 and vs.
and vs.
![${\rm [Fe/H]}$](/articles/aa/full_html/2009/35/aa10097-08/img35.png) ,
,
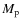 vs.
vs.
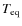 ). With recent
discoveries, this separation is still present in the Safronov number
distribution, but no longer in other diagrams. On the other hand,
our simulation predicts distributions that are continuous, in
particular in terms of Safronov number. With this continuous
distribution, we show that a random draw of 30 simulated planets
produces two spurious groups separated in Safronov number by a
distance equal to or larger than the observations in 30% of the
cases. The separation is not visible and significant between the two
classes in any other diagram we plotted. Therefore, we conclude that
the separation to two classes is not statistically significant but
is to be checked again with a larger sample of observed
planets. Interestingly, if on the contrary two classes of Safronov
numbers were found to exist we would have to revise our
model for the composition of planets.
). With recent
discoveries, this separation is still present in the Safronov number
distribution, but no longer in other diagrams. On the other hand,
our simulation predicts distributions that are continuous, in
particular in terms of Safronov number. With this continuous
distribution, we show that a random draw of 30 simulated planets
produces two spurious groups separated in Safronov number by a
distance equal to or larger than the observations in 30% of the
cases. The separation is not visible and significant between the two
classes in any other diagram we plotted. Therefore, we conclude that
the separation to two classes is not statistically significant but
is to be checked again with a larger sample of observed
planets. Interestingly, if on the contrary two classes of Safronov
numbers were found to exist we would have to revise our
model for the composition of planets.
Acknowledgements
The code used for this work, CoRoTlux, was developed as part of the CoRoT science program by the authors with major contributions by Aurélien Garnier, Maxime Marmier, Vincent Morello, Martin Vannier, and help from Suzanne Aigrain, Claire Moutou, Stéphane Lagarde, Antoine Llebaria, Didier Queloz, and François Bouchy. We thank F. Pont for many fruitful discussions on the subject, and the anonymous referee for a detailed review that helped improve the manuscript. F.F. was funded by a grant from the French Agence Nationale pour la Recherche. This work used Jean Schneider's exoplanet database www.exoplanet.eu, Frédéric Pont's table of transiting planets characteristics http://www.inscience.ch/transits/ and the Besançon model of the Galaxy at physique.obs-besancon.fr/modele/ extensively. The planetary evolution models used for this work can be downloaded at www.obs-nice.fr/guillot/pegasids/.
References
- Abramowitz, M., & Stegun, I. A. 1964, Handbook of Mathematical Functions, ninth dover printing, tenth gpo printing edn. (New York: Dover) (In the text)
- Aldrich, J., & Nelson, F. 1984, Linear Probability, Logit, and Probit Models (Sage Series on Quantitative Analysis) (In the text)
- Alonso, R., Brown, T. M., Torres, G., et al. 2004, ApJ, 613, L153 [NASA ADS] [CrossRef] (In the text)
- Alonso, R., Auvergne, M., Baglin, A., et al. 2008, A&A, 482, L21 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bakos, G., Noyes, R. W., Latham, D. W., et al. 2006, in Tenth Anniversary of 51 Peg-b: Status of and prospects for hot Jupiter studies, ed. L. Arnold, F. Bouchy, & C. Moutou, 184 (In the text)
- Bakos, G. Á., Shporer, A., Pál, A., et al. 2007, ApJ, 671, L173 [NASA ADS] [CrossRef]
- Barge, P., Baglin, A., Auvergne, M., et al. 2008, A&A, 482, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bouchy, F., Pont, F., Santos, N. C., et al. 2004, A&A, 421, L13 [NASA ADS] [CrossRef] [EDP Sciences]
- Bouchy, F., Pont, F., Melo, C., et al. 2005, A&A, 431, 1105 [NASA ADS] [CrossRef] [EDP Sciences]
- Bouchy, F., Queloz, D., Deleuil, M., et al. 2008, A&A, 482, L25 [NASA ADS] [CrossRef] [EDP Sciences]
- Burke, C. J., McCullough, P. R., Valenti, J. A., et al. 2007, ApJ, 671, 2115 [NASA ADS] [CrossRef]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef]
- Charbonneau, D., Winn, J. N., Latham, D. W., et al. 2006, ApJ, 636, 445 [NASA ADS] [CrossRef]
- Collier Cameron, A., Bouchy, F., Hebrard, G., et al. 2006, ArXiv Astrophys. e-prints (In the text)
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] (In the text)
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] (In the text)
- Fressin, F., Guillot, T., Morello, V., & Pont, F. 2007, A&A, 475, 729 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gaudi, B. S. 2005, ApJ, 628, L73 [NASA ADS] [CrossRef] (In the text)
- Gaudi, B. S., Seager, S., & Mallen-Ornelas, G. 2005, ApJ, 623, 472 [NASA ADS] [CrossRef]
- Gillon, M., Pont, F., Moutou, C., et al. 2006, A&A, 459, 249 [NASA ADS] [CrossRef] [EDP Sciences]
- Gillon, M., Pont, F., Moutou, C., et al. 2007, A&A, 466, 743 [NASA ADS] [CrossRef] [EDP Sciences]
- Greene, W. H. 2000, Econometric Analysis, fourth edition edn. (Prentice Hall International, International Edition) (In the text)
- Guillot, T. 2008, Phys. Scr. T, 130, 014023 [NASA ADS] [CrossRef]
- Guillot, T., & Showman, A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences]
- Hansen, B. M. S., & Barman, T. 2007, ApJ, 671, 861 [NASA ADS] [CrossRef] (In the text)
- Holman, M. J., Winn, J. N., Latham, D. W., et al. 2006, ApJ, 652, 1715 [NASA ADS] [CrossRef]
- Knutson, H. A., Charbonneau, D., Noyes, R. W., Brown, T. M., & Gilliland, R. L. 2007, ApJ, 655, 564 [NASA ADS] [CrossRef]
- Konacki, M., Sasselov, D. D., Torres, G., Jha, S., & Kulkarni, S. R. 2003, in BAAS, 1416
- Kovács, G., Bakos, G. Á., Torres, G., et al. 2007, ApJ, 670, L41 [NASA ADS] [CrossRef]
- Mandushev, G., O'Donovan, F. T., Charbonneau, D., et al. 2007, ApJ, 667, L195 [NASA ADS] [CrossRef]
- Mazeh, T., Zucker, S., & Pont, F. 2005, MNRAS, 356, 955 [NASA ADS] [CrossRef]
- McCullough, P. R., Stys, J. E., Valenti, J. A., et al. 2006, ApJ, 648, 1228 [NASA ADS] [CrossRef] (In the text)
- Minniti, D., Fernández, J. M., Díaz, R. F., et al. 2007, ApJ, 660, 858 [NASA ADS] [CrossRef]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- O'Donovan, F. T., Charbonneau, D., Mandushev, G., et al. 2006, ApJ, 651, L61 [NASA ADS] [CrossRef]
- O'Donovan, F. T., Charbonneau, D., Bakos, G. Á., et al. 2007, ApJ, 663, L37 [NASA ADS] [CrossRef]
- Pont, F., Bouchy, F., Queloz, D., et al. 2004, A&A, 426, L15 [NASA ADS] [CrossRef] [EDP Sciences]
- Pont, F., Bouchy, F., Melo, C., et al. 2005, A&A, 438, 1123 [NASA ADS] [CrossRef] [EDP Sciences]
- Pont, F., Zucker, S., & Queloz, D. 2006, MNRAS, 373, 231 [NASA ADS] [CrossRef] (In the text)
- Pont, F., Tamuz, O., Udalski, A., et al. 2008, A&A, 487, 749 [NASA ADS] [CrossRef] [EDP Sciences]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sato, B., Fischer, D. A., Henry, G. W., et al. 2005, ApJ, 633, 465 [NASA ADS] [CrossRef]
- Shporer, A., Tamuz, O., Zucker, S., & Mazeh, T. 2007, MNRAS, 136
- Smith, A. M. S., Collier Cameron, A., Christian, D. J., et al. 2006, MNRAS, 373, 1151 [NASA ADS] [CrossRef] (In the text)
- Southworth, J., Wheatley, P. J., & Sams, G. 2007, MNRAS, 379, L11 [NASA ADS] [CrossRef] (In the text)
- Sozzetti, A., Yong, D., Torres, G., et al. 2004, ApJ, 616, L167 [NASA ADS] [CrossRef]
- Torres, G., Konacki, M., Sasselov, D. D., & Jha, S. 2004, ApJ, 609, 1071 [NASA ADS] [CrossRef]
- Torres, G., Bakos, G. Á., Kovács, G., et al. 2007, ApJ, 666, L121 [NASA ADS] [CrossRef]
- Torres, G., Winn, J. N., & Holman, M. J. 2008, ApJ, 677, 1324 [NASA ADS] [CrossRef] (In the text)
- Udalski, A. 2003, Acta Astron., 53, 291 [NASA ADS] (In the text)
- Winn, J. N., Noyes, R. W., Holman, M. J., et al. 2005, ApJ, 631, 1215 [NASA ADS] [CrossRef]
- Winn, J. N., Holman, M. J., Bakos, G. Á., et al. 2007a, AJ, 134, 1707 [NASA ADS] [CrossRef]
- Winn, J. N., Holman, M. J., & Fuentes, C. I. 2007b, AJ, 133, 11 [NASA ADS] [CrossRef]
- Winn, J. N., Holman, M. J., Henry, G. W., et al. 2007c, AJ, 133, 1828 [NASA ADS] [CrossRef]
Online Material
Appendix A: Statistical evaluation of the model
A.1. Univariate tests on individual planet characteristics
Table 6: Mean values and standard deviations of the system parameters for the observed transiting planets and our simulated detections.
In this section, we detail the statistical method and tests that have been used to validate the model. We first perform basic tests of our model with simulations repeating multiple times the number of observations of the OGLE survey in order to get 50 000 detections. This number was chosen as a compromise between statistical significance and computation time. Table 6 compares the mean values and standard variations in the observations and in the simulations. The closeness of the values obtained for the two populations is an indication that our approach provides a reasonably good fit to the real stellar and planetary populations, and to the real planet compositions and evolution.
However, we do require more advanced statistical tests. First, we
use the so-called Student's t-test to formally compare the mean
values of all characteristics for both types of planets. The
intuition is that, should the model yield simulated planets of
attributes similar to real planets, the average values of these
attributes should not be significantly different from one another.
In other words, the so-called null hypothesis H0 is that the
difference of their mean is zero. Posing H0:
![]() where superscripts r and s denote real and simulated planets
respectively, and the alternative hypothesis
where superscripts r and s denote real and simulated planets
respectively, and the alternative hypothesis ![]() being the
complement
being the
complement ![]() :
:
![]() ,
we compute the tstatistics using the first and second moments of the distribution of
each planet characteristics as follows:
,
we compute the tstatistics using the first and second moments of the distribution of
each planet characteristics as follows:
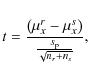 |
(2) |
where x is each of the planet characteristics, n is the size of each sample, and
Next, we perform the Kolmogorov-Smirnov test to allow for a more
global assessment of the compatibility of the two populations. This
test has the advantage of being non-parametric, making no assumption
about the distribution of data. This is particularly important since
the number of real planets remains small, which may alter the
normality of the distribution. Moreover, the Kolmogorov-Smirnov
comparison tests the stochastic dominance of the entire
distribution of real planets over simulated planets. To do so, it
computes the largest absolute deviations D between Fr(x), the
empirical cumulative distribution function of characteristics xfor real planets, and Fs(x) the cumulative distribution
function of characteristics x for simulated planets, over the
range of values of x:
![]() .
If the calculated D-statistic is greater than
the critical D*-statistic (provided by the Kolmogorov-Smirnov table: for 31
observations D*=0.19 for a 80% confidence level and D*=0.24 for a
95% confidence level), then one
must reject the null hypothesis that the two distributions are
similar,
H0: | Fr(x)-Fs(x) | <D*, and accept
.
If the calculated D-statistic is greater than
the critical D*-statistic (provided by the Kolmogorov-Smirnov table: for 31
observations D*=0.19 for a 80% confidence level and D*=0.24 for a
95% confidence level), then one
must reject the null hypothesis that the two distributions are
similar,
H0: | Fr(x)-Fs(x) | <D*, and accept
![]() .
Table 8 shows the
result of the test. The first column provides the D-Statistics, and
the second column gives the probability that the two samples have
the same distribution.
.
Table 8 shows the
result of the test. The first column provides the D-Statistics, and
the second column gives the probability that the two samples have
the same distribution.
Again, we find a good match between the model and observed samples: the parameters that have the least satisfactory fits are the planet's equilibrium temperature and the planet mass. These values are interpreted as being due to imperfections in the assumed star and planet populations. It is important to stress that although the extrasolar planets' main characteristics (period, mass) are well-defined by radial-velocity surveys, the subset of transiting planets is highly biased towards short periods and corresponds to a relatively small sample of the known radial-velocity planet population. This explains why the probability that the planetary mass is drawn from the same distribution in the model and in the observations is relatively low, which may otherwise seem surprising given that the planet mass distribution would be expected to be relatively well defined by the radial-velocity measurements.
A.2. Tests in two dimensions
Tests of the adequation of observations and models in two dimensions, i.e. when considering one parameter compared to another one can be performed using the method of maximum likelihood as described in Paper I. Table 9 provides values of the standard deviations from maximum likelihood for important combinations of parameters. The second column is a comparison using all planets discovered by transit surveys, and the third column using all known transiting planets (including those discovered by radial velocity).
The results are generally good, with deviations not exceeding
![]() .
They are also very similar when considering all
planets or only the subset discovered by photometric surveys. This
shows that the radial-velocity and photometric planet characteristics
are quite similar. The mass vs. radius relation shows the highest deviation,
as a few planets are outliers of our planetary evolution model.
.
They are also very similar when considering all
planets or only the subset discovered by photometric surveys. This
shows that the radial-velocity and photometric planet characteristics
are quite similar. The mass vs. radius relation shows the highest deviation,
as a few planets are outliers of our planetary evolution model.
A.3. Multivariate assessment of the performance of the model
A.3.1. Principle
Tests such as the Student-t statistics and the Kolmogorov-Smirnov test are important to determine the adequacy of given parameters, but they do not provide a multivariate assessment of the model. In order to globally assess the viability of our model we proceed as follows: We generate a list including 50 000 ``simulated'' planets and the 31 ``observed'' giant planets from Table 1. This number is necessary for an accurate multi-variate analysis (see Sect. A.3.2). A dummy variable Y is generated with value 1 if the planet is observed, 0 if the planet is simulated.
In order to test dependencies between parameters, we have presented in
Table 3 (Sect. 2.4) the Pearson
correlation coefficients between each variable including Y. A first
look at the table shows that the method correctly retrieves the
important physical correlations without any a priori information
concerning the links that exist between the different parameters. For
example, the stellar effective temperature
![]() is positively
correlated to the stellar mass
is positively
correlated to the stellar mass ![]() ,
and radius
,
and radius ![]() .
It is
also naturally positively correlated to the planet's equilibrium
temperature
.
It is
also naturally positively correlated to the planet's equilibrium
temperature
![]() ,
and to the planet's radius
,
and to the planet's radius ![]() simply because evolution models predict planetary radii that are
larger for larger values of the irradiation, all parameters being
equal. Interestingly, it can be seen that although the Safronov number
is by definition correlated to the planetary mass, radius, orbital
period and star mass (see Eq. (1)), the largest
correlation parameters for
simply because evolution models predict planetary radii that are
larger for larger values of the irradiation, all parameters being
equal. Interestingly, it can be seen that although the Safronov number
is by definition correlated to the planetary mass, radius, orbital
period and star mass (see Eq. (1)), the largest
correlation parameters for ![]() in absolute value are those related to
in absolute value are those related to ![]() and P (as the range of both these parameters vary by more
than one decade, while
and P (as the range of both these parameters vary by more
than one decade, while ![]() and
and ![]() only vary by a factor of
2). Also, we observe that the star metallicity is only correlated
to the planet radius. This is a consequence of our assumption that a
planet's heavy element content is directly proportional to the star's
[Fe/H], and of the fact that planets with more heavy elements are
smaller, all other parameters being equal. The planet's radius is
itself correlated negatively with [Fe/H] and positively with
only vary by a factor of
2). Also, we observe that the star metallicity is only correlated
to the planet radius. This is a consequence of our assumption that a
planet's heavy element content is directly proportional to the star's
[Fe/H], and of the fact that planets with more heavy elements are
smaller, all other parameters being equal. The planet's radius is
itself correlated negatively with [Fe/H] and positively with
![]() ,
,
![]() ,
,![]() and
and
![]() .
Table 3 also shows the correlations with
the ``reality'' parameter. Of course, a satisfactory model is one in
which there is no correlation between this reality parameter and other
physical parameters of the model. In our case, the corresponding
correlation coefficients are always small and indicate a good match
between the two populations.
.
Table 3 also shows the correlations with
the ``reality'' parameter. Of course, a satisfactory model is one in
which there is no correlation between this reality parameter and other
physical parameters of the model. In our case, the corresponding
correlation coefficients are always small and indicate a good match
between the two populations.
Table 7: Test of equality of means. Student's t value and critical probabilities p that individual parameters for both real and simulated planets have the same sample mean.
Table 8: Kolmogorov-Smirnov tests. D-statistics and critical probabilities that individual parameters for both real and simulated planets have the same distribution.
Table 9: Standard deviations from maximum likelihood of the model and observed transiting planet populations
Obviously the unconditional probability that a given planet is real
is
![]() .
Now we wish to know whether this
probability is sensitive to any of the planet characteristics,
controlling for all planet characteristics at once. Hence we model
the probability that a given planet is ``real'' using the logistic
cumulative density function as follows:
.
Now we wish to know whether this
probability is sensitive to any of the planet characteristics,
controlling for all planet characteristics at once. Hence we model
the probability that a given planet is ``real'' using the logistic
cumulative density function as follows:
where
Importantly, an ordinary least square estimator should not be used in
this framework, due to the binary nature of the dependent
variables. Departures from normality and predictions outside the
range [0;1] are the quintessential motivations. Instead, Eq. (4) can be estimated using maximum likelihood
methods. The so-called logit specification (Greene 2000) fits
the parameter estimates ![]() so as to maximize the log
likelihood function:
so as to maximize the log
likelihood function:
![\begin{displaymath}\log L({\vec{Y}}\vert{\vec{X,{b}}}) = \sum\limits_{i = 1}^n
{...
...^n {\log
\left[ {1 + {\rm e}^{{\vec{X}_i\vec{b} }} } \right]}.
\end{displaymath}](/articles/aa/full_html/2009/35/aa10097-08/img115.png) |
(5) |
The
Two features of logistic regression using
maximum likelihood estimators are important. First, the
value added by the exercise is that the multivariate approach allows
us to hold all other planet characteristics constant, extending the
bivariate correlations to the multivariate case. In other words, we
control for all planet characteristics at once. Second, one can test
whether a given parameter estimate is equal to 0 with the usual null
hypothesis H0: b=0 versus ![]() :
:
![]() .
The variance of
the estimator
.
The variance of
the estimator![]() is used
to derive the standard error of the parameter estimate.
Using Eq. (6), dividing each variable
is used
to derive the standard error of the parameter estimate.
Using Eq. (6), dividing each variable
![]() by the standard error
by the standard error
![]() yields
the t-statistics and allows us to test H0. We note
yields
the t-statistics and allows us to test H0. We note
![]() the probability that a higher value of t would occur by chance. This probability is evaluated for each explanatory variable
j. Should our model perform well, we would expect the t value
of each parameter estimate to be null, and the corresponding
probability
the probability that a higher value of t would occur by chance. This probability is evaluated for each explanatory variable
j. Should our model perform well, we would expect the t value
of each parameter estimate to be null, and the corresponding
probability
![]() to be close to one. This would imply no
significant association between a single planet characteristics and
the event of being a ``real'' planet.
to be close to one. This would imply no
significant association between a single planet characteristics and
the event of being a ``real'' planet.
The global probability that the model and
observations are compatible can be estimated. To do so, we compute
the log likelihood obtained when bj=0for j=1..m, where m is the number of variables. Following
Eq. (6):
The maximum of this quantity is
| (7) |
follows a
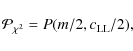 |
(8) |
where P(k,z) is the regularized Gamma function (e.g. Abramowitz & Stegun (1964)).
A.3.2. Determination of the number of model planets required
A problem that arose in the course of the present work was to evaluate
the number of model planets that were needed for the logit evaluation.
It is often estimated that about 10 times more model points than
observations are sufficient for a good tests. We found that
this relatively small number of points indeed leads to a valid
identification of the explanatory variables that are problematic,
i.e. those for which the ![]() coefficient is significantly
different from 0 (if any). However, the evaluation of the global
coefficient is significantly
different from 0 (if any). However, the evaluation of the global
![]() probability was then found to show considerable statistical
variability, probably given the relatively large number of explanatory
variables used for the study.
probability was then found to show considerable statistical
variability, probably given the relatively large number of explanatory
variables used for the study.
In order to test how the probability
![]() depends on the size
n of the sample to be analyzed, we first generated a very large list
of N0 simulated planets with CoRoTlux. We generated with
Monte-Carlo simulations a smaller subset of
depends on the size
n of the sample to be analyzed, we first generated a very large list
of N0 simulated planets with CoRoTlux. We generated with
Monte-Carlo simulations a smaller subset of
![]() simulated planets that
was augmented by the n1=31 observed planets and computed
simulated planets that
was augmented by the n1=31 observed planets and computed
![]() using the logit procedure. This exercise was performed 1000 times, and the results are
shown in Fig. 13. The resulting
using the logit procedure. This exercise was performed 1000 times, and the results are
shown in Fig. 13. The resulting
![]() is
found to be very variable for a sample smaller than
is
found to be very variable for a sample smaller than ![]() 20 000 planets. As a consequence, we chose to present tests performed for
n0=50 000 model planets.
20 000 planets. As a consequence, we chose to present tests performed for
n0=50 000 model planets.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{10097f14.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg132.png) |
Figure 13:
Values of the |
| Open with DEXTER | |
A.3.3. Analysis of two CoRoTlux samples
Table 4 (see Sect. 2.4) reports the
parameter estimates for each of the planet/star characteristics. We
start by assessing the general quality of the logistic regression by
performing the chi-square test. If the vector of planet
characteristics brings no or little information as to which type of
planets a given observation belongs, we would expect the logistic
regression to perform badly. In technical terms, we would expect the
conditional probability
![]() to be equal to the
unconditional probability
to be equal to the
unconditional probability
![]() .
The
.
The ![]() test described
above is used to evaluate the significance of the
model.
test described
above is used to evaluate the significance of the
model.
We performed several tests: the first column of results in
Table 10 shows the result of a logit
analysis with the whole series of 9 explanatory variables. Globally,
the model behaves well, with a likelihood statistic ratio
![]() and a
and a ![]() distribution for 9 degrees of freedom
yielding a probability
distribution for 9 degrees of freedom
yielding a probability
![]() .
When examining
individual variables, we find that the lowest probability derived from
the Student test is that of [Fe/H]:
.
When examining
individual variables, we find that the lowest probability derived from
the Student test is that of [Fe/H]:
![]() ,
implying that the stellar metallicity is not well reproduced. As
discussed previously, this is due to the fact that several planets of
the observed list have no or very poorly constrained determinations of
the stellar [Fe/H], and so a default value of 0 was then used.
,
implying that the stellar metallicity is not well reproduced. As
discussed previously, this is due to the fact that several planets of
the observed list have no or very poorly constrained determinations of
the stellar [Fe/H], and so a default value of 0 was then used.
The other columns in Table 10 show the
result of the logit analysis when removing one variable (i.e. with
only 8 explanatory variables). In agreement with the above analysis,
the highest global probability
![]() is obtained for the
model without the [Fe/H] variable. When removing other variables, the
results are very homogeneous, indicating that although the model can
certainly be improved, there is no readily identified problem except
that for [Fe/H]. We hope that future observations will allow for
better constraints on these stars' metallicities.
is obtained for the
model without the [Fe/H] variable. When removing other variables, the
results are very homogeneous, indicating that although the model can
certainly be improved, there is no readily identified problem except
that for [Fe/H]. We hope that future observations will allow for
better constraints on these stars' metallicities.
In order to further test the method, we show in
Table 11 the results of an analysis in which
the model radii where artificially augmented by 10%. The
corresponding probabilities are significantly lower: we
find that the model can explain the observations by chance only in
less than 1/10 000. The probabilities for each variable are affected
as well so that it is impossible to identify the culprit for the bad
fit with the 9 variables. However, when removing ![]() from the
analysis sample, the fit becomes significantly better. Note that
the results for that column are slightly different of those for the
same column in Table 10 because of the
dependance of
from the
analysis sample, the fit becomes significantly better. Note that
the results for that column are slightly different of those for the
same column in Table 10 because of the
dependance of ![]() on
on ![]() .
.
Table 10: Results of the logit analysis for the fiducial model with 50 000 model planets and 31 observations.
Table 11:
Results of the logit analysis for the altered model (![]() increased by 10%) with 50 000 model planets and 31
observations.
increased by 10%) with 50 000 model planets and 31
observations.
Footnotes
- ... population?
![[*]](/icons/foot_motif.png)
- Appendix is only available in electronic form at http://www.aanda.org
- ... planets
![[*]](/icons/foot_motif.png)
- we use Schneider's planet encyclopaedia: www.exoplanets.eu
- ...
) ![[*]](/icons/foot_motif.png)
- An electronic version of the table of simulated planets used to extrapolate radii is available at www.obs-nice.fr/guillot/pegasids/
- ... Paper I)
![[*]](/icons/foot_motif.png)
- Paper I shows how we estimate the deviation of real
planets from the maximimum likelihood of the model: in each 2-parameter space, we bin our data on a
 grid as a
compromise between resolution of the models and characteristic variations of the parameters.
The probability of an event in each bin is considered equal to the normalized number of
draws in that bin in our large model sample. The likelihood of a 31-planet draw is the sum of the logarithms
of the individual probablities of its events. We estimate the standard deviation of 1000 random 31-event draws among
the model detection sample, and calculate the deviation from maximum likelihood of the known planets as a function of this standard deviation.
grid as a
compromise between resolution of the models and characteristic variations of the parameters.
The probability of an event in each bin is considered equal to the normalized number of
draws in that bin in our large model sample. The likelihood of a 31-planet draw is the sum of the logarithms
of the individual probablities of its events. We estimate the standard deviation of 1000 random 31-event draws among
the model detection sample, and calculate the deviation from maximum likelihood of the known planets as a function of this standard deviation.
- ...
samples
![[*]](/icons/foot_motif.png)
- The pooled variance is computed as the sum of each
sample variance divided by the overall degree of freedom:
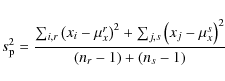
(3)
. - ... estimator
![[*]](/icons/foot_motif.png)
- The variance of the estimator is provided by
the Hessian
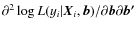 .
.
All Tables
Table 1: Characteristics of transiting planets included in this study.
Table 2: Characteristics of stars hosting the transiting planets included in this study
Table 3:
Pearson correlations between planetary and stellar characteristics.
Significant correlations (![]() 0.5) are boldfaced.
0.5) are boldfaced.
Table 4: Logistic maximum likelihood estimates.
Table 5: Mean planet radius for cool versus hot stars.
Table 6: Mean values and standard deviations of the system parameters for the observed transiting planets and our simulated detections.
Table 7: Test of equality of means. Student's t value and critical probabilities p that individual parameters for both real and simulated planets have the same sample mean.
Table 8: Kolmogorov-Smirnov tests. D-statistics and critical probabilities that individual parameters for both real and simulated planets have the same distribution.
Table 9: Standard deviations from maximum likelihood of the model and observed transiting planet populations
Table 10: Results of the logit analysis for the fiducial model with 50 000 model planets and 31 observations.
Table 11:
Results of the logit analysis for the altered model (![]() increased by 10%) with 50 000 model planets and 31
observations.
increased by 10%) with 50 000 model planets and 31
observations.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10097fg1.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg33.png) |
Figure 1: Distribution of stars as a function of their metallicity [Fe/H]. Upper panel: fraction of stars with planets as a function of their metallicity, as obtained from radial velocity surveys (Fischer & Valenti 2005; Santos et al. 2004). Bottom panel: normalized distribution of stellar metallicities assumed in Paper I (blue) and in this work (black). The resulting [Fe/H] distribution of planet-hosting stars is also shown in red. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg2.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg61.png) |
Figure 2:
Mass - radius relation for the transiting Pegasids discovered
to date (filled circles for planets with low Safronov number
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg3.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg62.png) |
Figure 3: Mass-period distribution of known short-period exoplanets. Crosses correspond to non-transiting planets discovered by radial-velocity surveys. Open and filled circles correspond to transiting planets (with Safronov numbers below and over 0.05, respectively). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg4.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg64.png) |
Figure 4: Planetary surface gravity versus orbital period of transiting giant planets discovered to date (circles) compared to a simulated joint probability density map (contours). Symbols and density plot are the same as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg5.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg66.png) |
Figure 5: Same figure as Fig. 4 with extended surface gravity and period ranges. Note that the scale of the color levels is logarithmic, in order to emphasize the presence of outliers. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg6.ps}\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg77.png) |
Figure 6: Stellar effective temperature versus planetary radius of transiting giant planets discovered to date (circles) compared to a simulated joint probability density map (contours). The black line is the sliding average of radii in the [-250 K,+250 K] effective temperature interval for all simulated transiting planets (both below and over the detection threshold). The white line is the same average for the detectable planets in the simulation. The symbols and density map are the same as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg7.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg85.png) |
Figure 7: Safronov number versus equilibrium temperature of transiting giant planets discovered to date (circles) compared to a simulated joint probability density map (contours). Open (resp. filled) circles correspond to class I (resp. class II) planets. The symbols and density map are the same as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg8.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg86.png) |
Figure 8: Comparison of the distribution of Safronov number between simulated detections (Red) and real events (Black). Top: histogram with 6 0.1-scale columns, Bottom: histogram with 12 0.05-scale columns. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097fg9.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg87.png) |
Figure 9: Occurrence of the largest observed separation of Safronov numbers between two ``groups'' selected from random draws among the model detections sample. The vertical line shows the separation (0.0102) between the two classes of planets as inferred from the observational sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097f10.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg90.png) |
Figure 10: Same as Fig. 7 but for a larger range of Safronov numbers. Note that the scale of the color levels is logarithmic, in order to emphasize the presence of outliers. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097f11.ps}\par\includegraphics[width=7.5cm,clip]{10097f12.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg91.png) |
Figure 11:
Planetary mass versus equilibrium temperature of
transiting giant planets discovered to date (circles) compared to
a simulated joint probability density map (contours). Top
panel: the density map accounts only for simulated planets
with a Safronov number
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10097f13.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg98.png) |
Figure 12: Safronov number of transiting planets as a function of their host star metallicity. The density map with linear contours comes from the model detection sample. Open and filled circles are respectively class I planets (with Safronov number over 0.05) and class II planets (with Safronov number below 0.05) Symbols and density plot are the same as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{10097f14.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa10097-08/Timg132.png) |
Figure 13:
Values of the |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}\theta = \frac{1}{2} \left[ \frac{V_{\rm esc}}{V_{\rm orb}} \right]^{2} =
\frac{a}{R_{\rm p}} \frac{M_{\rm p}}{M_{\star}},
\end{displaymath}](/articles/aa/full_html/2009/35/aa10097-08/img8.png)
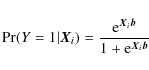
![\begin{displaymath}
\log L({\vec{Y}}\vert 1,b_0) = \sum\limits_{i = 1}^n
{y_i b_...
...um\limits_{i = 1}^n {\log
\left[ {1 + {\rm e}^{b_0}} \right]}.
\end{displaymath}](/articles/aa/full_html/2009/35/aa10097-08/img125.png)