EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 648 (April 2021) A&A, 648 (2021) A58 Full HTML
Free Access
Issue
A&A
Volume 648, April 2021
Article Number A58
Number of page(s) 14
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202037892
Published online 13 April 2021

© ESO 2021

1 Introduction

After the discovery of the first exoplanetary system around a pulsar (PSR 1257+12 b, c, d; Wolszczan & Frail 1992) with the pulsar timing technique, and of the first exoplanet orbiting a solar-type star (51 Peg b; Mayor & Queloz 1995) with the precise velocimetry, the photometric observations of planetary transits have proved to be the most successful way of detecting exoplanets.

Nearly 3000 out of about 4300 exoplanets were detected with the planetary transit method, most of them by just one project, Kepler/K2 (Borucki et al. 2010). Detailed characterizations of these systems requires both photometric (transits) and spectroscopic (radial velocities, abundances) observations, but not all of them are available for spectroscopic follow-up with ground-based instruments, due to the faintness of the hosts. This emphasizes the need for missions such as TESS (Ricker et al. 2015) and PLATO (Catala & PLATO Consortium 2008).

Our knowledge of exoplanets orbiting the solar-type or less massive stars on the main sequence (MS) is quite extensive due to the combined output of the RV and transit searches (see Winn & Fabrycky 2015 for a review). The domain of larger orbital separations or more evolved hosts clearly requires more exploration.

To date, the RV searches for exoplanets orbiting more evolved stars, such as the Lick K-giant Survey (Frink et al. 2002), Okayama Planet Search (Sato et al. 2003), Tautenberg Planet Search (Hatzes et al. 2005), Retired A Stars and Their Companions (Johnson et al. 2007), Pennsylvania-Toruń Planet Search (Niedzielski et al. 2007; Niedzielski & Wolszczan 2008a,b), or Boyunsen Planet Search (Lee et al. 2011), have resulted in a rather modest population of 112 substellar companions in 102 systems1.

The Pennsylvania-Toruń Planet Search (PTPS) is one of the most extensive RV searches for exoplanets around evolved stars. The project was designed to use the Hobby-Eberly Telescope (HET; Tull 1998) and its High-Resolution Spectrograph (HRS; Ramsey et al. 1998). It has surveyed a sample of stars distributed across the northern sky, with the typical, apparent V -magnitudes between 7.5 and 10.5 mag, and the B–V colour indices between 0.6 and 1.3. On the Hertzsprung-Russell diagram, these stars occupy an area delimited by the MS, the instability strip, and the coronal dividing line (Linsky & Haisch 1979). In total, the program sample of 885 stars contains 515 giants, 238 subgiants, and 132 dwarfs (Deka-Szymankiewicz et al. 2018). A detailed description of this sample, including their atmosphericand integrated parameters (masses, luminosities, and radii), is presented in a series of papers: Zieliński et al. (2012); Adamów et al. (2014); Niedzielski et al. (2016a); Adamczyk et al. (2016); Deka-Szymankiewicz et al. (2018). The first detection of a gas giant orbiting a red giant star by the PTPS project was reported by Niedzielski et al. (2007).

So far, 23 planetary systems have been detected by the PTPS and TAPAS projects. The most interesting ones include: a multiple planetary system around TYC 1422-00614-1, an evolved solar-mass K2 giant with two planets orbiting it (Niedzielski et al. 2015a); TYC 3667-1280-1, the most massive (1.9 M⊙), a red giant star hosting a warm Jupiter (Niedzielski et al. 2016b); and BD+48 740, a Li overabundant giant star with a planet, which possibly represents a case of recent engulfment (Adamów et al. 2012). Of specific interest is BD+14 4559 b, a 1.5 MJ gas giant orbiting a 0.9 M⊙ dwarf in an eccentric orbit (e = 0.29) at a distance of a = 0.78 au from the host star (Niedzielski et al. 2009a). The International Astronomical Union chose this planet and its host on the occasion of its 100th anniversary, to be named by the Polish national poll organized by the ExoWorlds project. They have been assigned the names of Pirx and Solaris to honor the famous Polish science fiction writer Stanisław Lem.

The PTPS sample is large enough to investigate planet occurrence as a function of a well-defined set of stellar parameters. For instance, the sample of 15 Li-rich giants has been studied in a series of papers (Adamów et al. 2012, 2014, 2015, 2018), and resulted in the discovery of 3 Li-rich giants with planetary-mass companions (BD+48 740, HD 238914, and TYC 3318-01333-1) and two planetary-mass companion candidates (TYC 3663-01966-1 and TYC 3105-00152-1). Another interesting subsample of the PTPS contains 115 stars with masses greater than 1.5 M⊙. So far, four giants with planets were detected in that sample, HD 95127, HD 216536, BD+49 828 (Niedzielski et al. 2015b), and TYC 3667-1280-1 (Niedzielski et al. 2016b), with masses as high as 1.87 M⊙. A 2.88 M⊙ giant TYC 3663-01966-1, mentioned above, also belongs to this subsample.

There are more PTPS stars to be investigated in the search for low-mass companions: 74 low-metallicity ([Fe/H] ≤−0.5) giants, including BD +20 2457 (Niedzielski et al. 2009a) and BD +03 2562 (Villaver et al. 2017), both with [Fe/H] ≤−0.7, and 57 high-luminosity giants with logL∕L⊙≥ 2, including BD +20 2457 (Niedzielski et al. 2009a) and HD 103485 (Villaver et al. 2017), both with log L∕L⊙≥ 2.5), and a number ofothers. All these investigations are still in progress. Here, we present the results for four of the program stars.

thumbnail Fig. 1

Hertzsprung-Russell diagram for 122 PTPS stars with solar masses within 5% uncertainty. The circles represent stars discussed in this work.

2 Sample and observations

There are 133 stars in the PTPS sample with masses in the 1 ± 0.05 M⊙ range: 12 dwarfs, 39 subgiants, and 82 giants (Deka-Szymankiewicz et al. 2018 and references therein). Due to an insufficient RV time series coverage (less than two epochs of observations), we removed 11 of these stars from further considerations. Consequently, the final, complete sample of 122 solar-mass stars contains 11 dwarfs, 33 subgiants, and 78 giant stars (Fig. 1). In what follows we call them elder suns, representing a range of evolutionary stages (from the MS through the subgiant branch and along the red giant branch (RGB)) and a range of metallicities (between [Fe/H] = −1.44 and [Fe/H] = +0.34, with [Fe/H] = −0.17 being the average). However, within the estimated uncertainties, their estimated masses are all the same. The small group of dwarfs included in the sample represents stars similar to the Sun with different metallicities. The sample defined this way allows us to study the planet occurrence ratio as a function of stellar metallicity for a fixed solar mass.

Here we present the results for four stars from this sample that show RV variations appearing to be caused by low-mass companions.Their basic atmospheric and stellar parameters are summarized in Table 1. The atmospheric parameters (Teff, log g, and [Fe/H]) were derived using a strictly spectroscopic method based on the LTE analysis of the equivalent widths of FeI and FeII lines by Zieliński et al. (2012). The estimates of the rotational velocities are given in Adamów et al. (2014). The stellar parameters (masses, luminosities, and radii) were estimated using the Bayesian approach of Jørgensen & Lindegren (2005), modified by da Silva et al. (2006), and adopted for our project by Adamczyk et al. (2016) using the theoretical stellar models from Bressan et al. (2012). In the case of BD+02 3313 we determined the luminosity using the Gaia Collaboration (2016) DR2 parallax (see Deka-Szymankiewicz et al. 2018 for details).

Table 1

Basic parameters of the program stars.

2.1 Observations

The spectroscopic observations presented in this paper were made with two instruments: the 9.2 m Hobby-Eberly Telescope (HET; Ramsey et al. 1998) and its High-Resolution Spectrograph (HRS; Tull 1998) in the queue scheduling mode (Shetrone et al. 2007), and the 3.58 m Telescopio Nazionale Galileo (TNG) and its High Accuracy Radial velocity Planet Searcher in the Northern hemisphere (HARPS-N; Cosentino et al. 2012). A detailed description of the adopted observing strategies and the instrumental configurations for both HET/HRS and TNG/HARPS-N can be found in Niedzielski et al. (2007, 2015a).

All HET/HRS spectra were reduced with the standard IRAF2 procedures. The TNG/HARPS-N spectra were processed with the standard user’s pipeline, Data Reduction Software (DRS; Pepe et al. 2002; Lovis & Pepe 2007).

2.2 Radial velocities

The HET/HRS is a general purpose spectrograph, which is neither temperature nor pressure-controlled. Therefore, the calibration of the RV measurements with this instrument is best accomplished with the I2 gas cell technique (Marcy & Butler 1992; Butler et al. 1996). Our application of this technique to HET/HRS data is described in detail in Nowak (2012) and Nowak et al. (2013).

The RVs from the HARPS-N were obtained with the cross-correlation method (Queloz 1995; Pepe et al. 2002). The wavelength calibration was done using the simultaneous Th-Ar mode of the spectrograph. The RVs were calculated by cross-correlating the stellar spectra with the digital mask for a K2 type star.

The RV data acquired with the two instruments are shown in Table 2. There are different zero point offsets between the data sets for every target listed in Table 3.

3 Keplerian analysis

To find the orbital parameters, we combined a global genetic algorithm (GA; Charbonneau 1995) with the MPFit algorithm (Markwardt 2009). This hybrid approach is described in Goździewski et al. (2003, 2007) and Goździewski & Migaszewski (2006). The range of the Keplerian orbital parameters found with the GA was searched with the RVLIN code (Wright & Howard 2009), which we modified to introduce the stellar jitter as a free parameter to be fitted in order to find the optimal solution (Ford & Gregory 2007; Johnson et al. 2011). The uncertainties were estimated with the bootstrap method described by Marcy et al. (2005).

For a more detailed description of the Keplerian analysis presented here, we refer the reader to the first TAPAS paper: Niedzielski et al. (2015a). The results of the analysis of our RV data are listed in Table 3.

3.1 HD 4760

HD 4760 (BD+05 109, TYC-0017-01084-1) is one of the least metal abundant giants in our sample, with ([Fe/H] = −0.91 ± 0.09). We measured the RVs for this star at 35 epochs over a period of approximately nine years. Twenty-five epochs of the HET/HRS data were obtained between January 12, 2006, and January 22, 2013 (2567 days, or ~7 yr). These data exhibit a RV amplitude of ± 839 m s−1. We also made ten additional observations of this star with the HARPS-N between November 30, 2012, and June 23, 2015 (935 days). For these observations the measured RV amplitude is 719 m s−1. These RV variations are more than two orders of magnitude larger than the estimated RV precision of our measurements.

The measured RVs show a statistically significant periodic signal in Lomb-Scargle periodogram (Lomb 1976; Scargle 1982; Press et al. 1992) (with a false alarm probability p < 10−3) with a peak at about 430 days (Fig. 2, top panel). These data, interpreted in terms of Keplerian motion, show that this star hosts a low-mass companion on an a = 1.14 au, eccentric (e = 0.23) orbit (Fig. 3). The calculated minimum mass of 13.9 ± 2.4 MJ, makes the system similar to the one hosted by BD+20 2457. See Table 3 and Fig. 3 for the details of the Keplerian model. After fitting this model out of the data, the remaining RV residuals leave no trace of a periodic signal (Fig. 2, bottom panel).

3.2 HD 96992

HD 96992 (BD+44 2063, TYC 3012-00145-1) is another low-metallicity ([Fe/H] = − 0.45 ± 0.08) giant in our sample. For this star we measured the RVs at 76 epochs over a 14-yr period. The HET/HRS data were obtained at 52 epochs between January 20, 2004, and February 06, 2013 (3305 days, or ~9 yr), showing a maximum amplitude of ± 157 m s−1. Twenty-fourmore epochs of the HARPS-N data were collected between December 16, 2012, and March 14, 2018 (1914 days, over 5 yr), resulting in a maximum RV amplitude of 117 m s−1.

The observed maximum RV amplitude is 25-100 times larger than the estimated RV precision. Our RV measurements show a statistically significant periodic signal (with a false alarm probability of about 10−3) with a peak at about 510 days (Fig. 4, top panel).

As the result of our Keplerian model fitting to data, this single periodic RV signal suggests that HD 96992 hosts an m sin i = 1.14 ± 1.1 MJ mass planet on an a = 1.24 au, eccentric orbit (e = 0.41). The parameters of this fit are listed in Table 3, and Fig. 5 shows the fit to RV data. As seen in Fig. 4 (bottom panel), after removing the Keplerian model, the RV residuals reveal yet another long-period signal of similar statistical significance to the 514-day signal, at a period of about 300 days.

We find this periodicity to be consistent with our estimate of the rotation period for HD 96992. To test alternative scenarios for this system, we tried to model a planetary system with two planets, but the dynamical modeling with Systemic 2.16 (Meschiari et al. 2009) shows that such a system is highly unstable and disintegrates after about 1000 yr. We also attempted to interpret the signal at 300 days as a single, Keplerian orbital motion, but it resulted in a highly eccentric orbit, and the quality of the fit was unsatisfactory. We therefore rejected these alternative solutions.

In conclusion, we postulate that the signal at 514 days, evident in the RV data for HD 96992 is due to Keplerian motion, and the signal at ~300 days remaining in the post-fit RV residuals reflects rotation of a feature on the stellar surface.

Table 3

Keplerian orbital parameters of companions to HD 4760, BD+02 3313, TYC 0434-04538-1, and HD 96992.

thumbnail Fig. 2

Lomb-Scargle periodogram of (from top to bottom) the combined HET/HRS and TNG/HARPS-N RV data, the selected photometric data set, the FWHM of the cross-correlation function from TNG, the SHK measured in TNG spectra, and the post Keplerian fit RV residua for HD 4760. A periodic signal is clearly present in the RV data.
thumbnail Fig. 3

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for HD 4760. The jitter is added to the uncertainties. Open symbols denote a repetition of the data points for the initial orbital phase.
thumbnail Fig. 4

Same as Fig. 2, but for HD 96992. The ≈300-day signal in RVresiduals is consistent with the estimated rotation period.
thumbnail Fig. 5

Same as Fig. 3, but for HD 96992.

3.3 BD+02 3313

BD+02 3313 (TYC 0405-01114-1) has a solar-like metallicity of [Fe/H] = 0.10 ± 0.07, but its luminosity is 27 times higher. We measured the RVs for this star at 29 epochs over 4264 days (11.6 yr). Thirteen epochs worth of HET/HRS RV data were gathered between July 11, 2006, and June 15, 2013 (2531 days, or ~ 7 yr). These RVs show a maximum amplitude of 1381 m s−1. Sixteen additional RV measurements were made with the HARPS-N between January 29, 2013, and March 14, 2018 (1870 days, or more than 5 yr). In this case, the maximum RV amplitude is 1141 m s−1, which is three orders of magnitude larger than the estimated RV precision. The data show a statistically significant periodic signal (with a false alarm probability of about 10−3) with a peak at about 1400 days (Fig. 6, top panel).

Interpreted in terms of the Keplerian motion, the available RVs show that this star hosts a low-mass companion, a brown dwarf, with a minimum mass of m sin i = 34.1 ± 1.1 MJ. The companion is located on an eccentric orbit (e = 0.47) at a = 2.47 au, within the brown dwarf desert (Marcy & Butler 2000), an orbital separation area below 3–5 au known for a paucity of brown dwarf companions to solar-type stars. The parameters of the Keplerian fit to these RV data are listed in Table 3, and shown in Fig. 7.

After removing the Keplerian model from the RV data, the residuals leave no sign of any leftover periodic signal (Fig. 6, bottom panel).

thumbnail Fig. 6

Same as Fig. 2, but for BD+02 3313.

3.4 TYC0434-04538-1

TYC 0434-04538-1 (GSC 00434-04538), another low-metallicity ([Fe/H] = −0.38 ± 0.06) giant, was observed 29 times over a period of 3557 days (9.7 yr). The HET/HRS measurements were made at 12 epochs, between June 23, 2008, and June 13, 2013 (over 1816 days, or nearly 5 yr), showing a maximum RV amplitude of ± 483 m s−1. Additional RV measurements for this star were made with the HARPS-N at 17 eopchs between June 27, 2013, and March 14, 2018 (1721 days, 4.7 yr). These data show a maximum RV amplitude of 442 m s−1, which is similar to that seen in the HET/HRS measurements. This is over two orders of magnitude more than the estimated RV precision. The data show a strong, statistically significant periodic signal (false alarm probability p < 10−3) with a peak at about 193 days (Fig. 8, top panel).

Our Keplerian analysis shows that this star hosts a 6.1 ± 1.1 MJ mass planet on an a = 0.66 au, almost circular (e = 0.08) orbit at the edge of the avoidance zone. The model parameters of the best Keplerian fit to data are presented in Table 3 and in Fig. 9.

After removing this model from the observed RV measurements we do not see any other periodic signal in the periodogram of the post-fit residuals (Fig. 8, bottom panel).

thumbnail Fig. 7

Same as Fig. 3, but for BD+02 3313.
thumbnail Fig. 8

Same as Fig. 2, but for TYC 0434-04538-1.
thumbnail Fig. 9

Same as Fig. 3, but for TYC 0434-04538-1.

4 Stellar variability and activity analysis

Stars beyond the MS, especially the red giants, exhibit activity and various types of variability that either alter their line profiles and mimic RV shifts or cause the line shifts. Such phenomena, if periodic, may be erroneously taken as evidence of the presence of orbiting low-mass companions.

A significant variability of the red giants has been already noted by Payne-Gaposchkin (1954) and Walker et al. (1989), and made the nature of these variations a topic of numerous studies. All the red giants of spectral type of K5 or later have been found to be photometrically variable, with increasing amplitudes for the cooler stars (Edmonds & Gilliland 1996; Henry et al. 2000).

Short-period RV variations in giants were demonstrated to originate from the p-mode oscillations by Hatzes & Cochran (1994). The first detection of multimodal oscillations in a K0 giant, α UMa, was published by Buzasi et al. (2000).

Solar-type p-mode (radial) oscillations (Kjeldsen & Bedding 1995; Corsaro et al. 2013) are easily observable in high-precision photometric time series measurements, and they have been intensely studied based on the COROT (Baglin et al. 2006) and Kepler (Gilliland et al. 2010)data, leading to precise mass determinations of many stars (De Ridder et al. 2009; Bedding et al. 2010; Kallinger et al. 2010; Hekker et al. 2011). Yu et al. (2020) present a Hertzsprung-Russel diagram with the amplitudes and frequencies of solar-like oscillations from the MS up to the tip of the RGB.

The granulation induced “flicker” (Corsaro et al. 2017; Tayar et al. 2019), on characteristic timescales of hours, is undoubtedly an additional unresolved component to the RV scatter in the red giants. Low-amplitude nonradial oscillations (mixed modes in Dziembowski et al. 2001) in the red giants (with frequencies of ≈5–60 cycles per day) were first detected by Hekker et al. (2006). They were later unambiguously confirmed using the COROT data by De Ridder et al. (2009), who also found that the lifetimes of these modes are on the order of a month. On the typical timescales for the red giants, ranging from hours to days, the short-period variations typically remain unresolved in low-cadence observations, focused on the long-term RV variations, and they contribute an additional uncertainty to the RV measurements.

In the context of planet searches, long-period variations of the red giant stars are more intriguing because they may masquerade as low-mass companions. Therefore, to distinguish between line profile shifts due to orbital motion and those caused, for instance, by pulsations, and line profile variations induced by stellar activity, it is crucial to understand processes that may cause the observed line shifts by studying the available stellar activity indicators.

As the HET/HRS spectra do not cover the spectral range where Ca II H & K lines are present, we use the line bisector and the Hα line index as activity indicators. In the case of TNG HARPS-N spectra, in addition to the RVs, the DRS provides the full width at half maximum (FWHM) of the cross-correlation function (CCF) between the stellar spectra and the digital mask and the line bisector (as defined in Queloz et al. 2001), both being sensitive activity indicators.

Table 4

Summary of the activity analysis.

Table 5

Summary of the activity analysis.

4.1 Line bisectors

The spectral line bisector (BIS) is a measure of the asymmetry of a spectral line, which can arise for such reasons as blending of lines, a surface feature (e.g., dark spots), oscillations, pulsations, and granulation (see Gray 2005 for a discussion of BIS properties). The BIS has proven to be a powerful tool to detect starspots and background binaries (Queloz et al. 2001; Santos et al. 2002) that can mimic a planet signal in the RV data. In the case of surface phenomena (cool spots), the anti-correlation between BIS and RV is expected (Queloz et al. 2001). In the case of a multiple star system with a separation smaller than that of the fiber of the spectrograph, the situation is more complicated; a correlation, anti-correlation, or lack of correlation may occur, depending on the properties of the components (see Santerne et al. 2015 and Günther et al. 2018 for a discussion). Unfortunately, for the slow-rotating giant stars like our targets, the BIS is not a sensitive activity indicator (Santos et al. 2003, 2014).

The HET/HRS and the HARPS-N bisectors are defined differently and were calculated from different instruments and spectral line lists. They are not directly comparable and have to be considered separately. All the HET/HRS spectral line bisector measurements were obtained from the spectra used for the I2 gas-cell technique (Marcy & Butler 1992; Butler et al. 1996). The combined stellar and iodine spectra were first cleaned of the I2 lines by dividing them by the corresponding iodine spectra imprinted in the flat-field spectra, and then cross-correlated with a binary K2 star mask. A detailed description of this procedure is described in Nowak et al. (2013). As stated in Sect. 2.2, HET/HRS is not a stabilized spectrograph, and the lack of correlation for BIS should be treated with caution, as it might be a result of the noise introduced by the varying instrumental profile.

The bisector inverse slopes of the cross-correlation functions from the HARPS-N data were obtained with the Queloz et al. (2001) method, using the standard HARPS-N user’s pipeline, which utilizes the simultaneous Th-Ar calibration mode of the spectrograph and the cross-correlation mask with a stellar spectrum (K2 in our case).

In all the cases presented here, the RVs do not correlate with the line bisectors at the accepted significance level (p = 0.01), see Tables 4 and 5. We conclude, therefore, that the HET/HRS and the HARPS-N BIS data have not been influenced by spots or background binaries.

4.2 The I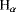 activity index

The Hα line is a widely used indicator of the chromospheric activity, as the core of this line is formed in the chromosphere. The increased stellar activity shows a correspondingly filled Hα profile. Variations in the flux in the line core can be measured with the 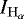activity index, defined as the ratio of the flux in a band centered on the Hα to the sum of fluxes in the reference bands. We have measured the Hα activity index (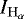) in both the HET/HRS and the TNG/HARPS-N spectra using the procedure described in Maciejewski et al. (2013; see also Gomes da Silva et al. 2012 or Robertson et al. 2013 and references therein).

The HET/HRS spectra were obtained via the iodine cell technique, meaning that the iodine spectrum was imprinted on the stellar spectrum. To remove the weak iodine lines in the Hα region, we divided the order of spectrum with the Hα by the corresponding order of the GC flat spectrum before performing the 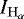index analysis.

A summary of our 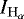analysis in the HET/HRS data is shown in Table 4, and a summary of the HARPS-N 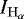data analysis is presented in Table 5. No statistically significant correlation between 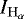and the RV datahas been found for our sample stars.

Table 6

Summary of long photometric time series available.

4.3 Calcium H & K doublet

The reversal profile in the cores of the Ca H and K lines (i.e., the emission structure at the core of the Ca absorption lines) is another commonly used indicator of stellar activity (Eberhard & Schwarzschild 1913). The Ca II H & K lines are located at the blue end of the TNG/HARPS-N spectra, which is the region with the lowest S/N for our red targets. The S/N of the spectra for the stars discussed here varies between 2 and 10. Stacking the spectra to obtain a better S/N is not possible here as they were taken at least a month apart. For every epoch’s usable spectrum for a given star, we calculated the SHK index following the formula of Duncan et al. (1991), and we calibrated it against the Mount Wilson scale with the formula provided in Lovis et al. (2011). We also searched the SHK indices for variability and found none (see periodograms in Figs. 2, 4, 6, and 8). Therefore, we conclude that the determined SHK indices are not related to the observed RV variations.

4.4 Photometry

Stellar activity and pulsations can also manifest themselves through changes in the brightness of a star. All our targets were observed by large photometric surveys. We collected the available data for them from several different catalogs: ASAS (Pojmanski 1997), NSVS (Woźniak et al. 2004), Hipparcos (Perryman & ESA 1997), and SuperWASP (Pollacco et al. 2006). We then selected the richest and the most precise data set from all the available ones for a detailed variability and period search. The original photometric time series were binned by one-day intervals. We found no periodic signal in the selected time series photometry for any of our targets (see periodograms in Figs. 2, 4, 6, and 8). Table 6 summarizes the results for the selected data.

thumbnail Fig. 10

Radial velocities plotted against cross-correlation function FWHM for TNG/HARPS-N data.

4.5 CCF FWHM

The stellar activity and surface phenomena impact the shape of the lines in the stellar spectrum. The properties of CCF, the mean profile of all spectral lines, are used as activity indicators. In a recent paper Oshagh et al. (2017) found the CCF FWHM to be the best indicator of stellar activity available from the HARPS-N DRS (for main sequence sun-like stars), in agreement with the previous results of Queloz et al. (2009) and Pont et al. (2011). These authors recommend it to reconstruct the stellar RV jitter as the CCF FWHM correlates well with the activity-induced RV in the stars of various activity levels.

For all the HARPS-N observations available for our targets, we correlated the FWHM of the CCF against the RV measurements for the TNG/HARPS-N data set. The presence of a correlation means that the observed variability may stem from distorted spectral lines, possibly due to stellar activity. The results of this analysis are shown in Table 5 and in Fig. 10. In the case of BD+02 3313 we found a statistically significant correlation (r = 0.73 > rc = 0.62) at the accepted confidence level of p = 0.01 between the observed RV and the CCF FWHM.

We also searched the CCF FWHM from HARPS-N for variability but found no statistically significant signal (see periodograms in Figs. 2, 4, 6, and 8).

5 Discussion

Hatzes & Cochran (1993) suggested that the low-amplitude long-period RV variations in red giants are attributable to pulsations, stellar activity (e.g., a spot rotating with a star), or low-mass companions. Such RV variations have been successfully demonstrated to be due to a presence of low-mass companions to many giants. Starting from ι Dra (Frink et al. 2002), 112 giants with planets are listed in the compilation by Sabine Reffert3. For some giants, however, the companion hypothesis has been debatable.

The nature of the observed RV long-term variability in some giants (O’Connell 1933; Payne-Gaposchkin 1954; Houk 1963) remains a riddle. Long secondary-period (LSP) photometric variations of AGB stars, and also of the luminous red giant stars (K5-M) near the tip of the first giant branch (TFGB) brighter than log L/L⊙ ~ 2.7, were detected in the MACHO data (Wood et al. 1999; their sequence D in the period-luminosity relation for the variable semi-regular giants), and OGLE data (Soszyński 2007; Soszyński et al. 2009, 2011, 2013). They associate the primary (but not always stronger) pulsations in these stars with periods that are typically ≈10 times shorter (usually on sequence B, first-overtone pulsations, of Wood et al. 1999). Depending on the adopted detection limit, 30–50% of luminous red giants may display LSP (Soszynski et al. 2007). With photometric amplitudes on the order of 1 mag, periods ranging from 250 to 1400 days, and RV amplitudes of 2–7 km s−1 (Wood et al. 2004; Nicholls et al. 2009), LSPs in luminous giants should be easily detectable in precise RV planet searches.

Soszynski et al. (2004a), following suggestions by Ita et al. (2002) and Kiss & Bedding (2003), demonstrated that in the LMC, LSPs are also present in stars below the TFGB, in the first ascent giants. These stars, OGLE Small Amplitude Red Giants (OSARGs; Wray et al. 2004), show much lower amplitudes (< 0.13mag in I band).

The origin of LSPs is practically unknown. Various scenarios, including the eccentric motion of an orbiting companion of mass ≈0.1 M⊙, radial and nonradial pulsations, rotation of an ellipsoidal-shaped red giant, episodic dust ejection, and starspot cycles, are discussed in Wood et al. (2004). These authors propose a composite effect of large-amplitude nonradial, g+ mode pulsation, and strong starspot activity as the most feasible model. Soszyński & Udalski (2014) proposed another scenario, a low-mass companion in a circular orbit just above the surface of the red giant, followed by a dusty cloud that regularly obscures the giant and causes the apparent luminosity variations. More recently, Saio et al. (2015) proposed oscillatory convective modes as another explanation for the LSP. These models, however, cannot explain effective temperatures of AGB stars (log L∕ L⊙≥ 3, M∕ M⊙ = 2) and periods at the same time.

Generally, the observational data seem to favour binary-type scenarios for LSP in giants, as for shorter periods the sequence D coincides with the E sequence of Wood et al. (1999), formed by close binary systems, in which one of the components is a red giant deformed due to the tidal force (Soszynski et al. 2004b; Nicholls & Wood 2012). Sequence E appears then to be an extension of the D sequence towards lower luminosity giants and some of the LSP cases may be explained by ellipsoidal variability (Soszynski et al. 2004b). See Nicholls & Wood 2012 for a discussion of differences of properties of pulsating giants in sequences D and E.

Recently, Lee et al. (2014, 2016), and Delgado Mena et al. (2018) invoked LSP as a potential explanation of observed RV variations in HD 216946 (M0 Iab var, logg = 0.5 ± 0.3, R = 350 R⊙, M = 6.8 ± 1.0 M⊙), μ UMa (M0 III SB, Teff = 3899 ± 35K, logg = 1.0, M = 2.2 M⊙, R = 74.7 R⊙, L = 1148 L⊙), and NGC 4349 No. 127 (L = 504.36 L⊙, logg = 1.99 ± 0.19, R = 36.98 ± 4.89 R⊙, M = 3.81 ± 0.23 M⊙).

An interesting case of Eltanin (γ Dra), a giant with RV variations that disappeared after several years, was recently discussed by Hatzes et al. (2018). This M = 2.14 ± 0.16 M⊙ star (R = 49.07 ± 3.75 R⊙ and L = 510 ± 51 L⊙, op. cit.; [Fe/H] = +0.11 ± 0.09, Teff = 3990 ± 42 K, and logg = 1.669 ± 0.1, Koleva & Vazdekis 2012) exhibited periodic RV variations that mimicked an m sin i = 10.7 MJ companion in 702-day orbit between 2003 and 2011. In the more recent data, collected between 2011 and 2017, these variations disappeared. The nature of this type of variability is unclear. The authors suggest a new form of stellar variability, possibly related to oscillatory convective modes (Saio et al. 2015).

Aldebaran (α Tau) was studied in a series of papers (Hatzes & Cochran 1993, 1998) in search of the origin of observed long-term RV variations. Hatzes et al. (2015), based on 30-yr observations, put forward a planetary hypothesis for this M = 1.13 ± 0.11 M⊙ giant star (Teff = 4055 ± 70 K, log g = 1.20 ± 0.1, and [Fe/H] = −0.27 ± 0.05, R = 45.1 ± 0.1 R⊙, op.cit.). They proposed a m sin i = 6.47 ± 0.53 MJ planet in 629-day orbit and a 520-day rotation modulation by a stellar surface structure. Recently, Reichert et al. (2019) showed, in 2006–2007, that the statistical power of the ≈620-day period exhibited a temporary but significant decrease. They also noted an apparent phase shift between the RV variations and orbital solution at some epochs. These authors note the resemblance of this star and γ Dra, and also point to the oscillatory convective modes of Saio et al. (2015) as the source of observed variations.

Due to the unknown underlying physics of the LSP, these claims are difficult to dispute. However, a mysterious origin of the LSP certainly makes luminous giants very intriguing objects, especially in the context of searching for low-mass companions around them.

Other phenomena that can mimic low-mass companions in precise RV measurements are starspots rotating with the stellar disk. They can affect spectral line profiles of magnetically active stars and mimic periodic RV variations caused by orbiting companions (Vogt et al. 1987; Walker et al. 1992; Saar & Donahue 1997).

Slowly rotating large G and K giants are not expected to exhibit strong surface magnetic fields. Nevertheless, they may show activity in the form of emission in the cores of strong chromospheric lines, photometric variability, or X-ray emission (Korhonen 2014). In their study of 17 377 oscillating red giants from Kepler, Ceillier et al. (2017) found that only 2.08% of the stars show a pseudo-periodic photometric variability likely originating from surface spots (a frequency consistent with the fraction of spectroscopically detected, rapidly rotating giants in the field).

The most extreme example of a slowly rotating giant with a relatively strong magnetic field of 100 G (Aurière et al. 2008) is EK Eri. Strassmeier et al. (1999) found this star to be a 14 L⊙, 1.85 M⊙ GIV-III giant with Teff = 5125 K, log g = 3.25, and photometric period of 306.9 ± 0.4 days. A detailed spectroscopic study by Dall et al. (2005) shows RV variations of about 100 m s−1 with the rotation period and a positive correlation between RV and BIS. In a following extensive study of this object, Dall et al. (2010) constrain the atmospheric parameters, suggest that the rotation period is twice the photometric period Prot = 2Pphot = 617.6 days, and present a 1979-2009 V photometry time series. The amplitude of the periodic variations is about 0.3 mag.

Another example is Pollux (β Gem), a slowly rotating M = 2.3 ± 0.2 M⊙ giant with a detected magnetic field (Lyubimkov et al. 2019). In a series of papers (Hatzes & Cochran 1993; Larson et al. 1993; Reffert et al. 2006) it was found to have a planetary-mass companion in a 589.7 ± 3.5-day orbit, and no sign of activity. This result was confirmed by Hatzes et al. (2006), who also estimated the star’s rotation period to be 135 days. Aurière et al. (2009) detected a weak magnetic field of −0.46 ± 0.04 G in Pollux, and Aurière et al. (2014) proposed a two-spot model that might explain the observed RV variations. However, in their model “photometric variations of larger amplitude than those detected in the Hipparcos data were predicted.” In their recent paper Aurière et al. (2021) find that the longitudinal magnetic field of Pollux varies with a sinusoidal behavior and a period of 660 ± 15 days, similar to that of the RV variations.

The presence of spots on a stellar surface may mimic low-mass companions if the spots show a similar repetitive pattern for a sufficiently long period of time. However, very little is known about the lifetime of spots on the surface of single inactive slowly rotating giants. Mosser et al. (2009) estimate that spots may form on the surface of F–G-type MS stars for a duration of 0.5-2 times the rotation period. Hall et al. (1990) studied the evolution of four spots on the surface of long-period RS CVN binary V1817 Cygni (K2III), and estimated their lifetimes to be two years. In addition, Gray & Brown (2006) identified a magnetically active region on the surface of Arcturus (K2 III) that lasted for a period of 2.0 ± 0.2 yr (the star was found to present a weak magnetic field by Sennhauser & Berdyugina 2011). Brown et al. (2008) published observationsthat suggest migration of an active region on the surface of Arcturus on a timescale of 115-253 days. A similar result, suggesting a0.5–1.3-yr recurrence period in starspot emergence, was derived in the case of a rapidly rotating K1IV star, KIC 11 560 447 (Özavcı et al. 2018).

The lifetime of spots on the surfaces of single, low-activity giants appears to be on the order of 2 yr. A long series of data covering several lifetimes of starspots is clearly required to rule out or confirm activity-related features as the origin of the observed RV variability.

5.1 HD 4760

HD 4760 is the most luminous and one of the most evolved stars in our sample, with log L∕L⊙ = 2.93 ± 0.11. Its large radius (R∕ R⊙ = 42 ± 9), low metallicity ([Fe/H] = −0.91 ± 0.09), and small logg = 1.62 ± 0.08 make it a twin to BD+20 2457, taking into account the estimated uncertainties.

The observed RV amplitude is about four times larger than the expected amplitude of the p-mode oscillations (see Table 4). We find that the actual RV jitter (σjitter) in HD 4760 is about three times smaller than that expected (Kosc) from the p-mode oscillations (Table 3). This discrepancy cannot be explained by the estimated uncertainties, and it suggests that they may have been underestimated in either luminosity or mass (or both).

The high luminosity of HD 4760 makes it an interesting candidate for an LSP object. However, the existing photometric data from ASAS do not indicate any variability. Moreover, our RV data covering about nine periods of the observed variation timescale, although not very numerous, do not show changes in amplitude or phase, while those detected in γ Dra or α Tau do (Fig. 11).

The rotation period of HD 4760 (1531 days) is highly uncertain and, given the uncertainties in v sin i and R⊙, its maximum value (Prot∕sin i) may range between 672 and 8707 days. The orbital period from the Keplerian fit to the RV data is shorter than the maximum allowed rotation period, and we cannot exclude the possibility that the periodic distortions of spectral lines by a spot rotating with the star are the reason for the observed RV variations. However, HD 4760 does not show anincreased activity (relative to the other stars in our sample) and none of activity indicators studied here is correlated with the observed RV variations. In addition, an estimate of the spot fraction that would cause the observed RV amplitude, based on the scaling relation of Hatzes (2002), gives a rather unrealistic value of f = 53[%]. Our data also show that the periodic RV variation has been present in HD 4760 for over nine years, which is unlikely if caused by a surface feature. Together with the apparent lack of photometric variability, we find that available data exclude that scenario.

We conclude that the presence of a companion appears to be the most likely hypothesis that explains the observed RV variations in HD 4760. The mass of the companion and a rather tight orbit of HD 4760 b locate it deep in the zone of engulfment (Villaver & Livio 2009; Villaver et al. 2014; Veras 2016). However, predicting its future requires a more detailed analysis as this relatively massive companion may survive the common envelope phase of this system’s evolution (Livio & Soker 1984). See Table 3 for details of the Keplerian model.

thumbnail Fig. 11

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for HD 4760. The jitter is added to the uncertainties. The RV data show no amplitude or phase shift over 9 yr of observations.

5.2 HD 96992

Of all the time series presented in this paper, this is certainly the noisiest one. The Keplerian model for the 514-day period results in a RV semi-amplitude of only 33 m s−1 (about five times greater than estimated HET/HRS precision), similar to the jitter of 20 m s−1 (Fig. 12). The observed RV amplitude is about 20 times larger than the expected amplitude of the p-mode oscillations. The jitter resulting from the Keplerian fit is larger than that expected from the scaling relations of Kjeldsen & Bedding (1995). This suggests an additional contribution, like granulation flicker, to the jitter.

HD 96992 is much less luminous than HD 4760, with log L∕L⊙ = 1.47 ± 0.09. It is located far below the TFGB, which makes it unlikely to be an irregular LSP giant. An apparent lack of photometric variability supports that claim as well.

The orbital period of 514 days is much longer than the estimated rotation period of 198 ± 92 days (Prot∕sin i = 128 − 332 days within uncertainties), which, together with absence of a photometric variability of similar period and no correlation with activity indicators, excludes a spot rotating with the star as the cause of the observed RV variations. The ≈ 300-day period present in the RV residua is more likely to be due to rotation.

The apparent absence of any correlation of the observed RV variations with activity indicators and no trace of periodic variations in those indices makes the Keplerian model the most consistent with the existing data. The details of our Keplerian model are shown in Table 3. The m sin i = 1.14 ± 0.31 MJ planet of this system orbits the star deep in the engulfment zone (Villaver & Livio 2009), and will most certainly be destroyed by its host before the AGB phase.

thumbnail Fig. 12

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for HD 96992. The jitter is added to the uncertainties.

5.3 BD+02 3313

BD+02 3313 is a very intriguing case of a solar metallicity giant. With log L∕L⊙ = 1.44 ± 0.24 it is located well below the TFGB, even below the horizontal branch, which makes it very unlikely to be a LSP pulsating red giant. The RV signal is very apparent; the Keplerian orbit suggests a RV semi-amplitude of 690 m s−1 and a period of 1393 days. These RV data show an amplitude over two orders of magnitude larger than that expected from the p-mode oscillations. The fitted jitter of 10 ms−1 is close to the expected from the scaling relations of Kjeldsen & Bedding (1995), within the uncertainties of mass and luminosity.

The estimated rotation period of 238 ± 122 days (Prot∕sin i = 146−421 days within the uncertainties) is much shorter than the Keplerian orbital period. The extensive photometric data set from ASAS, contemporaneous with our HET/HRS data, shows no periodic signal and no excess scatter that might be a signature of spots on the surface of the star.

None of the activity indices studied here shows a significant periodic signal. The line bisectors 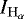and SHK are uncorrelated with the RV variations. The value of SHK does not indicate significant activity compared to other stars in our sample. The persistence of the RV periodicity for over 11 yr also advocates against a possible influence of an active region rotating with the star.

The resulting Keplerian model (Fig. 13), which suggests an m sin i = 34.1 ± 1.1 MJ companion in a 2.47 au, eccentric (e = 0.47) orbit (i.e., a brown dwarf in the brown dwarf desert) is consistent with the available RV data for the total time span of the observing run.

However, the FWHM of the CCF from the HARPS-N data for BD+02 3313 shows an r = 0.73 > rc = 0.62 correlation with the RV, which is statistically significant at the accepted confidence level of p = 0.01 (Fig. 10, lower left panel). Given the small number of CCF FWHM data points, we cannot exclude the possibility that the observed correlation is spurious. This possibility seems to be supported by the apparent lack of a periodic signal in the LS periodogram for CCF FWHM (Fig. 6).

An assumption that all the observed RV variations in this inactive star are due to the rotation of a surface feature is inconsistent with the existing photometry and our rotation period estimate. A more likely explanation would be the presence of a spatially unresolved companion associated with BD+02 3313.

We conclude that the observed RV and CCF FWHM correlation seriously undermines the Keplerian model of the observed RV variations in BD+02 3313. The actual cause of the reported RV variations remains to be identified with the help of additional observations.

thumbnail Fig. 13

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for BD+02 3313. The jitter is added to the uncertainties. The RV signal is very apparent.

5.4 TYC0434-04538-1

TYC 0434-04538-1 is a low-metallicity, [Fe/H] = −0.38 ± 0.06 giant, with aluminosity of logL∕L⊙ = 1.67 ± 0.09, which locates it near the horizontal branch. As such, the star is unlikely to be an irregular LSP giant.

It shows a strong periodic RV signal, which, when modelled under the assumption of Keplerian motion, shows a semi-amplitude of K = 209 m s−1, and a period of 193 days (Fig. 14). The RV data show an amplitude about 40 times larger than that expected of the p-mode oscillation. Again, the jitter is larger than expected form the p-mode oscillations only, so it likely contains an additional component, unresolved by our observations, like the granulation flicker.

This period is shorter than the estimate of Prot∕sin i = 124−225 days, hence the observed RV variation may originate, in principle, from a feature on the stellar surface rotating with the star. The spot would have to cover f = 10% of the stellar surface according to the simple model of Hatzes (2002) to explain the observed RV variations. Photometric data from ASAS,which show no variability, do not support this scenario. We also note that such a large spot coverage (10%) was successfully applied to model spots on the surface of the overactive spotted giant in binary system EPIC 211759736 by Oláh et al. (2018). Consequently, we conclude that the available data favor the low-mass companion hypothesis.

thumbnail Fig. 14

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for TYC 0434-04538-1. The jitter is added to the uncertainties. The RV variations appear to be stable over the period of nearly 10 yr.
thumbnail Fig. 15

Mass-orbital period relation for 228 planets hosted by solar-mass stars (within 5%) in exoplanets.org, together with our four new candidates presented here. Symbol sizes are scaled with orbital eccentricities.

5.5 Current status of the project

The sample contains 122 stars in total, with at least two epochs of observations that allowed us to measure the RV variation amplitude.

Sixty stars in the sample (49 ± 5%) are assumed to be single as they show ΔRV <50 m s−1 in several epochs of data over a period of, typically, 2–3 yr. This group of stars may still contain long-period and/or low-mass companions,which means that the number of single stars may be overestimated. Due to unavailable telescope time further observationsof these stars have ceased.

The estimate of single-star frequency in our sample, although based on a small sample of GK stars at various stages of evolution from the MS to the RGB, agrees with the results of a study of a sample of 454 stars by Raghavan et al. (2010) who found that 54 ± 2% of solar-type stars are single. We take this agreement as a confirmation that our sample is not biased towards binary or single stars.

Nineteen stars in our sample (16 ± 3%) are spectroscopic binaries with ΔRV > 2 km s−1. Technically not only HD 181368 b (Adamów et al. 2018), but also BD+20 274 b (Gettel et al. 2012) belongs to this group, due to the observed RV trend. Although we cannot exclude more low-mass companions associated with binary stellar systems for these targets, they were rejected from further observations after several epochs, due to the limited telescope time available.

Finally, 43 of the stars in our sample (35 ± 4%) show RV amplitudes between 50 m s−1 and 2 km s−1, and are assumed to be either active stars or planetary/BD companion candidates. We searched these stars for low-mass companions for this project.

Six low-mass companion hosts have been identified in the sample so far: HD 102272 (Niedzielski et al. 2009b), BD+20 2457 (Niedzielski et al. 2009a), BD+20 274 (Gettel et al. 2012), HD 219415 (Gettel et al. 2012), HD 5583 (Niedzielski et al. 2016c), and HD 181368 (Adamów et al. 2018).

This paper presents low-mass companions to another three stars: HD 4760, TYC 0434 04538 1, and HD 96992. Our findings addto a population of 228 planets orbiting solar-mass stars in exoplanets.org (Fig. 15).

Seven stars from the sample (HD 102272, BD+20 2457, BD+20 274, HD 219415, HD 5583, TYC 0434 04538 1, HD 96992) show RV variations consistent with planetary-mass companions (mp sin i < 13 MJ), which represents 6 ± 2% of the sample.

6 Conclusions

Based on precise RV measurements gathered with the HET/HRS and Harps-N for over 14 yr, we discussed three solar-mass giants with low-mass companions: HD 4760 hosts an m sin i = 13.9 ± 2.4 MJ companion in an a = 1.14 ± 0.08 au and e = 0.23 ± 0.09 orbit; HD 96992 has an m sin i = 1.14 ± 0.31 MJ companion in an a = 1.24 ± 0.05 au, eccentric e = 0.41 ± 0.24 orbit; TYC 0434-04538-1 is accompanied with an m sin i = 6.1 ± 0.7 MJ companion in an a = 1.66 ± 0.04 au, nearly circular orbit with e = 0.08 ± 0.05. In the case of BD+02 3313 we find the Keplerian model uncertain because of statistically significant correlation between RV and CCF FWHM in the HARPS-N data.

The analysis of RV amplitudes in our sample of 122 solar-mass stars at various stellar evolution stages shows that single-star frequency is 49 ± 5%, which means that the sample is not biased against stellar binarity.

Acknowledgements

We thank the HET and IAC resident astronomers and telescope operators for their support. A.N. was supported by the Polish National Science Centre grant no. 2015/19/B/ST9/02937. E.V. acknowledges support from the Spanish Ministerio de Ciencia Inovación y Universidades under grant PGC2018-101950-B-100. K.K. was funded in part by the Gordon and Betty Moore Foundation’s Data-Driven Discovery Initiative through Grant GBMF4561. This research was supported in part by PL-Grid Infrastructure. The HET is a joint project of the University of Texas at Austin, the Pennsylvania State University, Stanford University, Ludwig- Maximilians-Universität München, and Georg-August-Universität Göttingen. The HET is named in honor of its principal benefactors, William P. Hobby and Robert E. Eberly. The Center for Exoplanets and Habitable Worlds is supported by the Pennsylvania State University, the Eberly College of Science, and the Pennsylvania Space Grant Consortium. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This research has made use of NASA’s Astrophysics Data System. The acknowledgements were compiled using the Astronomy Acknowledgement Generator. This research made use of SciPy (Jones et al. 2001). This research made use of the yt-project, a toolkit for analyzing and visualizing quantitative data (Turk et al. 2011). This research made use of matplotlib, a Python library for publication quality graphics (Hunter 2007). This research made use of Astropy, a community-developed core Pythonpackage for Astronomy (Astropy Collaboration 2013). IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation (Tody 1993). This research made use of NumPy (Walt et al. 2011). We thank the referee for comments that have significantly contributed to improving this paper.

References

  1. Adamczyk, M., Deka-Szymankiewicz, B., & Niedzielski, A. 2016, A&A, 587, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Adamów, M., Niedzielski, A., Villaver, E., Nowak, G., & Wolszczan, A. 2012, ApJ, 754, L15 [Google Scholar]
  3. Adamów, M., Niedzielski, A., Villaver, E., Wolszczan, A., & Nowak, G. 2014, A&A, 569, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Adamów, M., M., Niedzielski, A., Villaver, E., et al. 2015, A&A, 581, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Adamów, M., Niedzielski, A., Kowalik, K., et al. 2018, A&A, 613, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Aurière, M., Konstantinova-Antova, R., Petit, P., et al. 2008, A&A, 491, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Aurière, M., Wade, G. A., Konstantinova-Antova, R., et al. 2009, A&A, 504, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Aurière, M., Konstantinova-Antova, R., Espagnet, O., et al. 2014, IAU Symp., 302, 359 [Google Scholar]
  10. Aurière, M., Petit, P., Mathias, P., et al. 2021, A&A, 646, A130 [EDP Sciences] [Google Scholar]
  11. Baglin, A., Auvergne, M., Barge, P., et al. 2006, ESA SP, 1306, 33 [Google Scholar]
  12. Bedding, T. R., Huber, D., Stello, D., et al. 2010, ApJ, 713, L176 [Google Scholar]
  13. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [Google Scholar]
  15. Brown, K. I. T., Gray, D. F., & Baliunas, S. L. 2008, ApJ, 679, 1531 [Google Scholar]
  16. Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
  17. Buzasi, D., Catanzarite, J., Laher, R., et al. 2000, ApJ, 532, L133 [Google Scholar]
  18. Catala, C., & PLATO Consortium 2008, J. Phys. Conf. Ser., 118, 012040 [Google Scholar]
  19. Ceillier, T., Tayar, J., Mathur, S., et al. 2017, A&A, 605, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Charbonneau, P. 1995, ApJS, 101, 309 [Google Scholar]
  21. Corsaro, E., Fröhlich, H. E., Bonanno, A., et al. 2013, MNRAS, 430, 2313 [NASA ADS] [CrossRef] [Google Scholar]
  22. Corsaro, E., Mathur, S., García, R. A., et al. 2017, A&A, 605, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Cosentino, R., Lovis, C., Pepe, F., et al. 2012, SPIE Conf. Ser., 8446 [Google Scholar]
  24. Dall, T. H., Bruntt, H., & Strassmeier, K. G. 2005, A&A, 444, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Dall, T. H., Bruntt, H., Stello, D., & Strassmeier, K. G. 2010, A&A, 514, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Deka-Szymankiewicz, B., Niedzielski, A., Adamczyk, M., et al. 2018, A&A, 615, A31 [CrossRef] [EDP Sciences] [Google Scholar]
  28. Delgado Mena, E., Lovis, C., Santos, N. C., et al. 2018, A&A, 619, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. De Ridder, J., Barban, C., Baudin, F., et al. 2009, Nature, 459, 398 [Google Scholar]
  30. Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [NASA ADS] [CrossRef] [Google Scholar]
  31. Dziembowski, W. A., Gough, D. O., Houdek, G., & Sienkiewicz, R. 2001, MNRAS, 328, 601 [Google Scholar]
  32. Eberhard, G., & Schwarzschild, K. 1913, ApJ, 38, 292 [Google Scholar]
  33. Edmonds, P. D., & Gilliland, R. L. 1996, ApJ, 464, L157 [Google Scholar]
  34. Ford, E. B., & Gregory, P. C. 2007, ASP Conf. Ser., 371, 189 [Google Scholar]
  35. Frink, S., Mitchell, D. S., Quirrenbach, A., et al. 2002, ApJ, 576, 478 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  36. Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Gettel, S., Wolszczan, A., Niedzielski, A., et al. 2012, ApJ, 756, 53 [Google Scholar]
  38. Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [Google Scholar]
  39. Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2012, A&A, 541, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Goździewski,K., & Migaszewski, C. 2006, A&A, 449, 1219 [EDP Sciences] [Google Scholar]
  41. Goździewski,K., Konacki, M., & Maciejewski, A. J. 2003, ApJ, 594, 1019 [Google Scholar]
  42. Goździewski, K., Maciejewski, A. J., & Migaszewski, C. 2007, ApJ, 657, 546 [Google Scholar]
  43. Gray, D. F. 2005, PASP, 117, 711 [Google Scholar]
  44. Gray, D. F., & Brown, K. I. T. 2006, PASP, 118, 1112 [Google Scholar]
  45. Günther, M. N., Queloz, D., Gillen, E., et al. 2018, MNRAS, 478, 4720 [Google Scholar]
  46. Hall, D. S., Gessner, S. E., Lines, H. C., & Lines, R. D. 1990, AJ, 100, 2017 [Google Scholar]
  47. Hatzes, A. P. 2002, Astron. Nachr., 323, 392 [Google Scholar]
  48. Hatzes, A. P., & Cochran, W. D. 1993, ApJ, 413, 339 [Google Scholar]
  49. Hatzes, A. P., & Cochran, W. D. 1994, ApJ, 432, 763 [Google Scholar]
  50. Hatzes, A. P., & Cochran, W. D. 1998, MNRAS, 293, 469 [Google Scholar]
  51. Hatzes, A. P., Guenther, E. W., Endl, M., et al. 2005, A&A, 437, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Hatzes, A. P., Cochran, W. D., Endl, M., et al. 2006, A&A, 457, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Hatzes, A. P., Cochran, W. D., Endl, M., et al. 2015, A&A, 580, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Hatzes, A. P., Endl, M., Cochran, W. D., et al. 2018, AJ, 155, 120 [Google Scholar]
  55. Hekker, S., Aerts, C., De Ridder, J., & Carrier, F. 2006, A&A, 458, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Hekker, S., Gilliland, R. L., Elsworth, Y., et al. 2011, MNRAS, 414, 2594 [Google Scholar]
  57. Henry, G. W., Fekel, F. C., Henry, S. M., & Hall, D. S. 2000, ApJS, 130, 201 [Google Scholar]
  58. Houk, N. 1963, AJ, 68, 253 [Google Scholar]
  59. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  60. Ita, Y., Tanabé, T., Matsunaga, N., et al. 2002, MNRAS, 337, L31 [Google Scholar]
  61. Johnson, J. A., Fischer, D. A., Marcy, G. W., et al. 2007, ApJ, 665, 785 [NASA ADS] [CrossRef] [Google Scholar]
  62. Johnson, J. A., Payne, M., Howard, A. W., et al. 2011, AJ, 141, 16 [Google Scholar]
  63. Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python [Google Scholar]
  64. Jørgensen, B. R., & Lindegren, L. 2005, A&A, 436, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Kallinger, T., Mosser, B., Hekker, S., et al. 2010, A&A, 522, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Kiss, L. L., & Bedding, T. R. 2003, MNRAS, 343, L79 [Google Scholar]
  67. Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
  68. Koleva, M., & Vazdekis, A. 2012, A&A, 538, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Korhonen, H. 2014, IAU Symp., 302, 350 [Google Scholar]
  70. Larson, A. M., Irwin, A. W., Yang, S. L. S., et al. 1993, PASP, 105, 825 [Google Scholar]
  71. Lee, B.-C., Mkrtichian, D. E., Han, I., Kim, K.-M., & Park, M.-G. 2011, A&A, 529, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Lee, B. C., Han, I., Park, M. G., Hatzes, A. P., & Kim, K. M. 2014, A&A, 566, A124 [EDP Sciences] [Google Scholar]
  73. Lee, B.-C., Han, I., Park, M.-G., et al. 2016, AJ, 151, 106 [Google Scholar]
  74. Linsky, J. L., & Haisch, B. M. 1979, ApJ, 229, L27 [Google Scholar]
  75. Livio, M., & Soker, N. 1984, MNRAS, 208, 763 [NASA ADS] [CrossRef] [Google Scholar]
  76. Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
  77. Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
  79. Lyubimkov, L. S., Petrov, D. V., & Poklad, D. B. 2019, Astrophysics, 62, 338 [Google Scholar]
  80. Maciejewski, G., Niedzielski, A., Wolszczan, A., et al. 2013, AJ, 146, 147 [Google Scholar]
  81. Marcy, G. W., & Butler, R. P. 1992, PASP, 104, 270 [NASA ADS] [CrossRef] [Google Scholar]
  82. Marcy, G. W., & Butler, R. P. 2000, PASP, 112, 137 [NASA ADS] [CrossRef] [Google Scholar]
  83. Marcy, G. W., Butler, R. P., Vogt, S. S., et al. 2005, ApJ, 619, 570 [Google Scholar]
  84. Markwardt, C. B. 2009, ASP Conf. Ser., 411, 251 [Google Scholar]
  85. Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
  86. Meschiari, S., Wolf, A. S., Rivera, E., et al. 2009, PASP, 121, 1016 [Google Scholar]
  87. Mosser, B., Baudin, F., Lanza, A. F., et al. 2009, A&A, 506, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Nicholls, C. P., & Wood, P. R. 2012, MNRAS, 421, 2616 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  89. Nicholls, C. P., Wood, P. R., Cioni, M. R. L., & Soszyński, I. 2009, MNRAS, 399, 2063 [Google Scholar]
  90. Niedzielski, A., & Wolszczan, A. 2008a, IAU Symp., 249, 43 [Google Scholar]
  91. Niedzielski, A., & Wolszczan, A. 2008b, ASP Conf. Ser., 398, 71 [Google Scholar]
  92. Niedzielski, A., Konacki, M., Wolszczan, A., et al. 2007, ApJ, 669, 1354 [NASA ADS] [CrossRef] [Google Scholar]
  93. Niedzielski, A., Nowak, G., Adamów, M., & Wolszczan, A. 2009a, ApJ, 707, 768 [Google Scholar]
  94. Niedzielski, A., Goździewski, K., Wolszczan, A., et al. 2009b, ApJ, 693, 276 [Google Scholar]
  95. Niedzielski, A., Villaver, E., Wolszczan, A., et al. 2015a, A&A, 573, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Niedzielski, A., Wolszczan, A., Nowak, G., et al. 2015b, ApJ, 803, 1 [Google Scholar]
  97. Niedzielski, A., Deka-Szymankiewicz, B., Adamczyk, M., et al. 2016a, A&A, 585, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Niedzielski, A., Villaver, E., Nowak, G., et al. 2016b, A&A, 589, L1 [EDP Sciences] [Google Scholar]
  99. Niedzielski, A., Villaver, E., Nowak, G., et al. 2016c, A&A, 588, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Nowak, G. 2012, PhD thesis, Nicolaus Copernicus Univ., Toruń, Poland [Google Scholar]
  101. Nowak, G., Niedzielski, A., Wolszczan, A., Adamów, M., & Maciejewski, G. 2013, ApJ, 770, 53 [Google Scholar]
  102. O’Connell, D. J. K. 1933, Harvard College Observ. Bull., 893, 19 [Google Scholar]
  103. Oláh, K., Rappaport, S., Borkovits, T., et al. 2018, A&A, 620, A189 [EDP Sciences] [Google Scholar]
  104. Oshagh, M., Santos, N. C., Figueira, P., et al. 2017, A&A, 606, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Özavcı, I., Şenavcı, H. V., Işık, E., et al. 2018, MNRAS, 474, 5534 [Google Scholar]
  106. Payne-Gaposchkin, C. 1954, Ann. Harvard College Observ., 113, 189 [Google Scholar]
  107. Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Perryman, M. A. C., & ESA 1997, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
  109. Pojmanski, G. 1997, Acta Astron., 47, 467 [Google Scholar]
  110. Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
  111. Pont, F., Aigrain, S., & Zucker, S. 2011, MNRAS, 411, 1953 [Google Scholar]
  112. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing (Cambridge: Cambridge University Press) [Google Scholar]
  113. Queloz, D. 1995, IAU Symp., 167, 221 [Google Scholar]
  114. Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Ramsey, L. W., Adams, M. T., Barnes, T. G., et al. 1998, SPIE Conf. Ser., 3352, 34 [Google Scholar]
  118. Reffert, S., Quirrenbach, A., Mitchell, D. S., et al. 2006, ApJ, 652, 661 [Google Scholar]
  119. Reichert, K., Reffert, S., Stock, S., Trifonov, T., & Quirrenbach, A. 2019, A&A, 625, A22 [CrossRef] [EDP Sciences] [Google Scholar]
  120. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
  121. Robertson, P., Endl, M., Cochran, W. D., & Dodson-Robinson, S. E. 2013, ApJ, 764, 3 [NASA ADS] [CrossRef] [Google Scholar]
  122. Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
  123. Saio, H., Wood, P. R., Takayama, M., & Ita, Y. 2015, MNRAS, 452, 3863 [NASA ADS] [CrossRef] [Google Scholar]
  124. Santerne, A., Díaz, R. F., Almenara, J. M., et al. 2015, MNRAS, 451, 2337 [Google Scholar]
  125. Santos, N. C., Mayor, M., Naef, D., et al. 2002, A&A, 392, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  126. Santos, N. C., Udry, S., Mayor, M., et al. 2003, A&A, 406, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Santos, N. C., Mortier, A., Faria, J. P., et al. 2014, A&A, 566, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Sato, B., Ando, H., Kambe, E., et al. 2003, ApJ, 597, L157 [Google Scholar]
  129. Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
  130. Sennhauser, C., & Berdyugina, S. V. 2011, A&A, 529, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Shetrone, M., Cornell, M. E., Fowler, J. R., et al. 2007, PASP, 119, 556 [Google Scholar]
  132. Soszyński, I. 2007, ApJ, 660, 1486 [Google Scholar]
  133. Soszyński, I., & Udalski, A. 2014, ApJ, 788, 13 [Google Scholar]
  134. Soszynski, I., Udalski, A., Kubiak, M., et al. 2004a, Acta Astron., 54, 129 [NASA ADS] [Google Scholar]
  135. Soszynski, I., Udalski, A., Kubiak, M., et al. 2004b, Acta Astron., 54, 347 [Google Scholar]
  136. Soszynski, I., Dziembowski, W. A., Udalski, A., et al. 2007, Acta Astron., 57, 201 [NASA ADS] [Google Scholar]
  137. Soszyński, I., Udalski, A., Szymański, M. K., et al. 2009, Acta Astron., 59, 239 [Google Scholar]
  138. Soszyński, I., Udalski, A., Szymański, M. K., et al. 2011, Acta Astron., 61, 217 [NASA ADS] [Google Scholar]
  139. Soszyński, I., Udalski, A., Szymański, M. K., et al. 2013, Acta Astron., 63, 21 [NASA ADS] [Google Scholar]
  140. Strassmeier, K. G., Stȩpień, K., Henry, G. W., & Hall, D. S. 1999, A&A, 343, 175 [NASA ADS] [Google Scholar]
  141. Tayar, J., Stassun, K. G., & Corsaro, E. 2019, ApJ, 883, 195 [Google Scholar]
  142. Tody, D. 1993, ASP Conf. Ser., 52, 173 [NASA ADS] [Google Scholar]
  143. Tull, R. G. 1998, SPIE Conf. Ser., 3355, 387 [Google Scholar]
  144. Turk, M. J., Smith, B. D., Oishi, J. S., et al. 2011, ApJS, 192, 9 [Google Scholar]
  145. Veras, D. 2016, R. Soc. Open Sci., 3, 150571 [Google Scholar]
  146. Villaver, E., & Livio, M. 2009, ApJ, 705, L81 [NASA ADS] [CrossRef] [Google Scholar]
  147. Villaver, E., Livio, M., Mustill, A. J., & Siess, L. 2014, ApJ, 794, 3 [NASA ADS] [CrossRef] [Google Scholar]
  148. Villaver, E., Niedzielski, A., Wolszczan, A., et al. 2017, A&A, 606, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  149. Vogt, S. S., Penrod, G. D., & Hatzes, A. P. 1987, ApJ, 321, 496 [Google Scholar]
  150. Walker, G. A. H., Yang, S., Campbell, B., & Irwin, A. W. 1989, ApJ, 343, L21 [Google Scholar]
  151. Walker, G. A. H., Bohlender, D. A., Walker, A. R., et al. 1992, ApJ, 396, L91 [Google Scholar]
  152. Walt, S. v. d., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [CrossRef] [Google Scholar]
  153. Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [Google Scholar]
  154. Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
  155. Wood, P. R., Alcock, C., Allsman, R. A., et al. 1999, IAU Symp., 191, 151 [Google Scholar]
  156. Wood, P. R., Olivier, E. A., & Kawaler, S. D. 2004, ApJ, 604, 800 [NASA ADS] [CrossRef] [Google Scholar]
  157. Woźniak, P. R., Vestrand, W. T., Akerlof, C. W., et al. 2004, AJ, 127, 2436 [Google Scholar]
  158. Wray, J. J., Eyer, L., & Paczyński, B. 2004, MNRAS, 349, 1059 [Google Scholar]
  159. Wright, J. T., & Howard, A. W. 2009, ApJS, 182, 205 [Google Scholar]
  160. Yu, J., Bedding, T. R., Stello, D., et al. 2020, MNRAS, 493, 1388 [Google Scholar]
  161. Zieliński, P., Niedzielski, A., Wolszczan, A., Adamów, M., & Nowak, G. 2012, A&A, 547, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
2

IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.

All Tables

Table 1

Basic parameters of the program stars.

In the text
Table 3

Keplerian orbital parameters of companions to HD 4760, BD+02 3313, TYC 0434-04538-1, and HD 96992.

In the text
Table 4

Summary of the activity analysis.

In the text
Table 5

Summary of the activity analysis.

In the text
Table 6

Summary of long photometric time series available.

In the text

All Figures

thumbnail Fig. 1

Hertzsprung-Russell diagram for 122 PTPS stars with solar masses within 5% uncertainty. The circles represent stars discussed in this work.
In the text
thumbnail Fig. 2

Lomb-Scargle periodogram of (from top to bottom) the combined HET/HRS and TNG/HARPS-N RV data, the selected photometric data set, the FWHM of the cross-correlation function from TNG, the SHK measured in TNG spectra, and the post Keplerian fit RV residua for HD 4760. A periodic signal is clearly present in the RV data.
In the text
thumbnail Fig. 3

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for HD 4760. The jitter is added to the uncertainties. Open symbols denote a repetition of the data points for the initial orbital phase.
In the text
thumbnail Fig. 4

Same as Fig. 2, but for HD 96992. The ≈300-day signal in RVresiduals is consistent with the estimated rotation period.
In the text
thumbnail Fig. 5

Same as Fig. 3, but for HD 96992.
In the text
thumbnail Fig. 6

Same as Fig. 2, but for BD+02 3313.
In the text
thumbnail Fig. 7

Same as Fig. 3, but for BD+02 3313.
In the text
thumbnail Fig. 8

Same as Fig. 2, but for TYC 0434-04538-1.
In the text
thumbnail Fig. 9

Same as Fig. 3, but for TYC 0434-04538-1.
In the text
thumbnail Fig. 10

Radial velocities plotted against cross-correlation function FWHM for TNG/HARPS-N data.
In the text
thumbnail Fig. 11

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for HD 4760. The jitter is added to the uncertainties. The RV data show no amplitude or phase shift over 9 yr of observations.
In the text
thumbnail Fig. 12

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for HD 96992. The jitter is added to the uncertainties.
In the text
thumbnail Fig. 13

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for BD+02 3313. The jitter is added to the uncertainties. The RV signal is very apparent.
In the text
thumbnail Fig. 14

Keplerian best fit to combined HET/HRS (orange) and TNG/HARPS-N (blue) data for TYC 0434-04538-1. The jitter is added to the uncertainties. The RV variations appear to be stable over the period of nearly 10 yr.
In the text
thumbnail Fig. 15

Mass-orbital period relation for 228 planets hosted by solar-mass stars (within 5%) in exoplanets.org, together with our four new candidates presented here. Symbol sizes are scaled with orbital eccentricities.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.