| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | L10 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201527563 | |
| Published online | 02 December 2015 | |
Online material
Appendix A: Grain size fitting
In order to calculate the maximum likelihood grain-size distribution, we compute the scattering and polarising properties of a grid of dust models under the assumption of Mie scattering (Mie 1908) by bare, compact spheres, which allows us to fit the observations under the assumption of single scattering. We assume a grain size distribution of the form ![]() , where a is the grain radius and
, where a is the grain radius and ![]() is the number density of grains with radius a. The lower- (amin) and upper- (amax) size limits are free parameters, and the exponent of the grain size distribution is fixed to q = 3.5. For each size distribution, we calculate the scattering and absorbtion cross-sections, and the components of the Müller matrix at one degree intervals, for each wavelength for which we wish to fit observations.
is the number density of grains with radius a. The lower- (amin) and upper- (amax) size limits are free parameters, and the exponent of the grain size distribution is fixed to q = 3.5. For each size distribution, we calculate the scattering and absorbtion cross-sections, and the components of the Müller matrix at one degree intervals, for each wavelength for which we wish to fit observations.
The polarisation fraction at each wavelength is completely determined by the elements of the Müller matrix, such that p(λ,θ) = |S12(λ,θ)/S11(λ,θ)|, where p is the polarisation fraction, λ is the wavelength of interest, θ is the scattering angle, and Sij are the elements of the Müller matrix.
The ratio of the scattered intensities at any pair of wavelengths is determined by the scattering phase function, contained within S11, and the ratio of the scattering efficiencies, i.e. 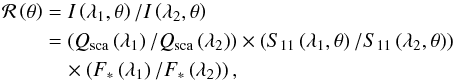 (A.1)where F∗ is the flux emitted by the star and Qsca are the scattering efficiencies. For each grain-size distribution, we calculate the likelihood
(A.1)where F∗ is the flux emitted by the star and Qsca are the scattering efficiencies. For each grain-size distribution, we calculate the likelihood 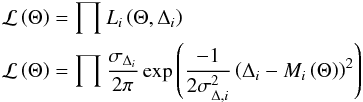 where Δ is a vector of observations such that Δi is the ith observation and σΔi its associated uncertainty, Mi is the output of the model associated with the ith observation, and Θ is a vector of model parameters (in our case
where Δ is a vector of observations such that Δi is the ith observation and σΔi its associated uncertainty, Mi is the output of the model associated with the ith observation, and Θ is a vector of model parameters (in our case ![]() ). The maximum-likelihood model is then defined to be the model with parameters Θ that maximises the value of
). The maximum-likelihood model is then defined to be the model with parameters Θ that maximises the value of ![]() , and Θ contains the information in which we are interested.
, and Θ contains the information in which we are interested.
For the sake of efficiency, it is common to compute the log-likelihood 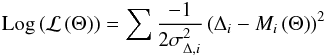 by taking only the exponent.
by taking only the exponent.
By calculating a grid of grain-size distributions with 5 nm <amin ≤ 1μm and 100 nm <amax ≤ 50 μm we cover the full range of grain sizes observed in the interstellar medium and in the circumstellar environments of evolved stars. The resulting likelihood space for the S Knot is shown in Fig. A.1, zoomed to show the region of interest.
 |
Fig. A.1
Likelihood space for scattering angle of 63°, corresponding to the S Knot, zoomed to show grain sizes in the range 0.1−3 μm. |
| Open with DEXTER | |
The average size of the maximum-likelihood distribution is calculated simply from 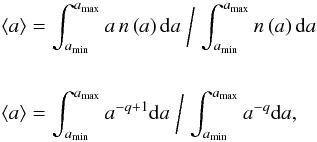 which can be solved analytically.
which can be solved analytically.
Because the scattering properties are determined by the real part of the complex refractive index of the grain material, which is similar for all of the plausible choices, the optical properties are dominated by the grain size for a ~ λ, rather than the choice of silicate material.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


