| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526673 | |
| Published online | 27 October 2015 | |
Online material
Appendix A: Flux received by the ring
Here, we detail the computation of the flux Fr(φi) received by the ring per unit area. The notation is the same as in Sect. 3.1 of the main text (see also Fig. 2). The general expression of the flux derived from Eqs. (10) and (11) is 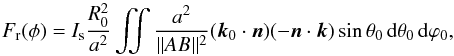 (A.1)where
(A.1)where 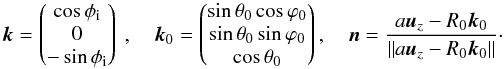 (A.2)The integrand in the expression of Fr is of order unity. We expand it at the first order in R0/a ≪ 1. We get
(A.2)The integrand in the expression of Fr is of order unity. We expand it at the first order in R0/a ≪ 1. We get 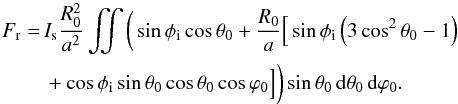 (A.3)We consider the most general case where each element of the ring only sees a fraction of the stellar disk (see Fig. A.1). This case happens when the tilt angle φi is less than the angular radius of the star . In this configuration, the visible surface is delimited by two curves: the arc CDE in the xy-plane of the star and bounded by −π/ 2−ϕa ≤ ϕ0 ≤ π/ 2 + ϕa, and the arc EC, which is half of a circle of radius R0cosϕa in the plane of the ring. For commodity, we recall the definition of the angle ϕa given in Eq. (14)
(A.3)We consider the most general case where each element of the ring only sees a fraction of the stellar disk (see Fig. A.1). This case happens when the tilt angle φi is less than the angular radius of the star . In this configuration, the visible surface is delimited by two curves: the arc CDE in the xy-plane of the star and bounded by −π/ 2−ϕa ≤ ϕ0 ≤ π/ 2 + ϕa, and the arc EC, which is half of a circle of radius R0cosϕa in the plane of the ring. For commodity, we recall the definition of the angle ϕa given in Eq. (14) ![]() To compute the surface integral (A.3), we make use of the Stockes theorem that transforms a surface integral over Σ into a closed integral over its boundary ∂Σ as
To compute the surface integral (A.3), we make use of the Stockes theorem that transforms a surface integral over Σ into a closed integral over its boundary ∂Σ as 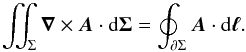 (A.4)For this problem, we set
(A.4)For this problem, we set 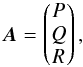 (A.5)where
(A.5)where 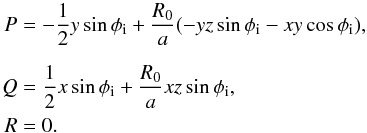 (A.6)
(A.6)
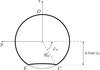 |
Fig. A.1
Area enclosed by the thick curve CDEC is the visible part of the star seen from an element of the ring. |
| Open with DEXTER | |
For the line integral CDE, we use r = (x,y,z) with ![]() (A.7)where ϕ0 goes from (− π/ 2−ϕa) to (π/ 2 + ϕa),. While for the line integral EC, we set r = (x,y,z) with
(A.7)where ϕ0 goes from (− π/ 2−ϕa) to (π/ 2 + ϕa),. While for the line integral EC, we set r = (x,y,z) with 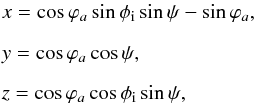 (A.8)where ψ ranges from 0 to π. As a result, we get
(A.8)where ψ ranges from 0 to π. As a result, we get 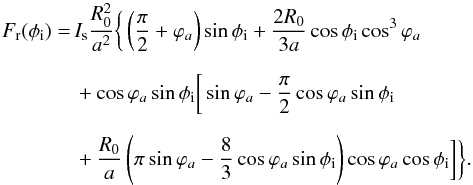 (A.9)In the case where φi>φc, Eq. (A.9) still holds if we set ϕa = π/ 2 so we get
(A.9)In the case where φi>φc, Eq. (A.9) still holds if we set ϕa = π/ 2 so we get 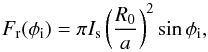 while for φi ≪ φc, ϕa ~ aφi/R0 and
while for φi ≪ φc, ϕa ~ aφi/R0 and 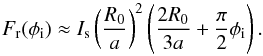
Appendix B: Reflectivity
The reflectivity of the ring is computed by assuming an isotropic scattering. Furthermore, it is assumed that given an incoming flux Fr, only a fraction ![]() is re-emitted in the visible spectrum. Thus, the luminous intensity Ir of the rings is uniform and such that
is re-emitted in the visible spectrum. Thus, the luminous intensity Ir of the rings is uniform and such that ![]() (B.1)Besides this, the flux received on Earth from the disk is
(B.1)Besides this, the flux received on Earth from the disk is ![]() (B.2)where the ratio of the projected surface Sproj of the rings on the plane of the sky divided by the square of the distance D to the Earth represents the solid angle under which the rings are seen. As a result, we get
(B.2)where the ratio of the projected surface Sproj of the rings on the plane of the sky divided by the square of the distance D to the Earth represents the solid angle under which the rings are seen. As a result, we get 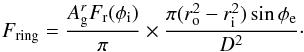 (B.3)Moreover, the stellar flux F⋆ received on Earth is
(B.3)Moreover, the stellar flux F⋆ received on Earth is 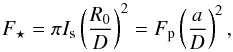 (B.4)
(B.4)
where we used Fp = πIs(R0/a)2. Combining Eqs. (B.3) and (B.4), we get 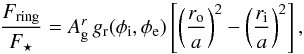 (B.5)with gr a function representing the reflectivity of the rings given by
(B.5)with gr a function representing the reflectivity of the rings given by 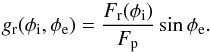 (B.6)
(B.6)
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


