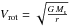| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526673 | |
| Published online | 27 October 2015 | |
Detecting ring systems around exoplanets using high resolution spectroscopy: the case of 51 Pegasi b⋆,⋆⋆
1 Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
e-mail: nuno@astro.up.pt
2 Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
3 ASD, IMCCE-CNRS UMR8028, Observatoire de Paris, UPMC, 77 Av. Denfert-Rochereau, 75014 Paris, France
4 CIDMA, Departamento de Física, Universidade de Aveiro, Campus de Santiago, 3810-193 Aveiro, Portugal
5 European Southern Observatory, Casilla 19001, Santiago, Chile
6 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
7 Observatoire de Genève, Université de Genève, 51 ch. des Maillettes, 1290 Sauverny, Switzerland
8 Scientific Support Office, Directorate of Science and Robotic Exploration, ESA/ESTEC, Keplerlaan 1, 2201 AZ, Noordwijk, The Netherlands
Received: 4 June 2015
Accepted: 4 August 2015
Aims. In this paper we explore the possibility that the recently detected reflected light signal of 51 Peg b could be caused by a ring system around the planet.
Methods. We use a simple model to compare the observed signal with the expected signal from a short-period giant planet with rings. We also use simple dynamical arguments to understand the possible geometry of such a system.
Results. We provide evidence that, to a good approximation, the observations are compatible with the signal expected from a ringed planet, assuming that the rings are non-coplanar with the orbital plane. However, based on dynamical arguments, we also show that this configuration is unlikely. In the case of coplanar rings we then demonstrate that the incident flux on the ring surface is about 2% the value received by the planet, a value that renders the ring explanation unlikely.
Conclusions. The results suggest that the signal observed cannot in principle be explained by a planet+ring system. We discuss, however, the possibility of using reflected light spectra to detect and characterize the presence of rings around short-period planets. Finally, we show that ring systems could have already been detected by photometric transit campaigns, but their signal could have been easily misinterpreted by the expected light curve of an eclipsing binary.
Key words: techniques: spectroscopic / planets and satellites: dynamical evolution and stability / planets and satellites: rings / planetary systems
Based on observations collected at ESO facilities under program 091.C-0271 (with the HARPS spectrograph at the ESO 3.6-m telescope, La Silla-Paranal Observatory).
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The detection of the atmospheres of extrasolar planets is becoming one of the major research topics in the exoplanet field (for a recent review see Burrows 2014). Current technology and a detailed data analysis have already allowed the signature of the atmospheres of other worlds to be detected using different methods, such as transmission spectroscopy (e.g., Charbonneau et al. 2002; Vidal-Madjar et al. 2003; Madhusudhan et al. 2014), occultations (e.g., Deming et al. 2005; Demory et al. 2012), and phase curve variations (e.g., Angerhausen et al. 2014). These studies allowed several detailed analyses of exoplanet atmospheres, including tracing of thermal or albedo maps of the planets (e.g., Knutson et al. 2007; Stevenson et al. 2014; Demory et al. 2013).
Although a large majority of the exoplanet atmosphere studies involved space-based data, the use of ground-based instrumentation to detect exoplanet atmospheres is providing a growing amount of information. This is particularly true concerning the use of high-resolution spectroscopic techniques. Using both optical and the near-infrared (near-IR) wavelengths, these methods allowed the spectrum to be probed in detail for several exoplanets (for some examples see Snellen et al. 2010; Birkby et al. 2013; Wyttenbach et al. 2015).
In a recent paper, Martins et al. (2015) have explored a new technique for detecting the signature of a high-resolution (optical) reflected light spectrum from an exoplanet. This detection allowed estimation of the radius and albedo of the historical 51 Peg b planet (Mayor & Queloz 1995), suggesting that this planet may be a high-albedo, inflated hot-Jupiter such as Kepler-7 b (with Ag = 0.35Demory et al. 2013).
The predicted star-to-planet flux ratio for a star+planet system be estimated from (e.g., Seager 2010): 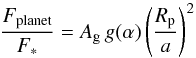 (1)where Ag is the geometric albedo of the planet, a the semi-major axis of the orbit, g(α) the phase function, and Rp the planetary radius. The full width at half maximum (FWHM) (22.6 ± 3.6 km s-1) and amplitude (6.0 ± 0.4 × 10-5) of the detected planet-cross-correlation function (CCF), as detected in Martins et al. (2015), when compared to the values of the stellar CCF (7.47 km s-1 and 0.48, respectively), would lead to a planet-to-star flux ratio of 3.8 × 10-4. By applying the equation above, we would then derive a geometric albedo far above unity if we assume a jovian-like radius for 51 Peg b1.
(1)where Ag is the geometric albedo of the planet, a the semi-major axis of the orbit, g(α) the phase function, and Rp the planetary radius. The full width at half maximum (FWHM) (22.6 ± 3.6 km s-1) and amplitude (6.0 ± 0.4 × 10-5) of the detected planet-cross-correlation function (CCF), as detected in Martins et al. (2015), when compared to the values of the stellar CCF (7.47 km s-1 and 0.48, respectively), would lead to a planet-to-star flux ratio of 3.8 × 10-4. By applying the equation above, we would then derive a geometric albedo far above unity if we assume a jovian-like radius for 51 Peg b1.
Martins et al. (2015) presented the results of some simulations suggesting that the observed (and larger than expected) FWHM broadening can be an artifact produced by non-Gaussian noise in the data, together with the fact that their detection was only possible at a three-sigma level. The authors thus only used a comparison of the CCF depths to derive indicative values for the albedo and planetary radius. (The two parameters are degenerate.) Martins et al. also suggested that the parameters of the CCF should be taken just as indicative, even if they consider the detection solid.
It is, however, interesting to explore the possibility that the observed CCF values are real. In this case, what could explain such a wide and deep CCF as observed? One possibility for explaining the large FWHM would be the presence of strong winds or a very fast rotation velocity (close to the observed FWHM). The signature of strong winds in exoplanets has indeed been observed using transmission spectroscopy (e.g., Snellen et al. 2010). However, such broadening of the CCF would also imply a decrease in its depth. The wind explanation would thus not be able to explain the total surface of the CCF. Some extra component would be needed. Besides this, though not discussed directly in the paper, the near-IR signal of 51 Peg b detected by Brogi et al. (2013) using CO lines does not seem to show a clear sign of extra broadening (see their Fig. 3). Winds should produce a broadening that is independent of the wavelength of the observations.
In the present paper we explore a new interpretation of the measurements done by Martins et al. In particular, we try to understand if the signal detected could be explained by a reflective ring system around 51 Peg b. The existence of such rings has already been demonstrated to be possible around hot-Jupiters (e.g., Schlichting & Chang 2011). In Sect. 2 we unveil our hypothesis based on the observations of Martins et al. (2015), and we explore how a ring system should be able to explain the observed signal at opposition, i.e., when the Earth, the star, and the planet are almost aligned (in the same order). In this study, we assume that the rings are not coplanar with the planet orbit and provide the results as a function of the angle φ between the Earth-star-planet line and the ring plane. In Sect. 3 we use dynamical constraints to investigate whether the necessary configuration corresponds to a physical scenario. A more detailed model of the reflected light from a coplanar ring system is then explored in Sect. 3.1. In Sect. 4 we briefly show that rings may have already been detected using transit photometry, though in some cases their signature could have been interpreted as caused by the eclipse of a stellar companion. We conclude in Sect. 5.
2. The case for rings: a simple model
In Eq. (1) we denote the planet-to-star flux ratio expected for a star+planet system. The presence of rings around the planet would alter this ratio, because these would also reflect light toward the observer.
The orbital inclination of 51 Peg b is close to 80 degrees (Brogi et al. 2013; Martins et al. 2015). Moreover, in Martins et al. (2015), the detection of the reflected light has been done almost at opposition. Thus, to get a rough estimation of the reflected light in this condition, we assume a simple geometry of the problem in which the Earth, the star, and the planet are along a straight line. In this configuration, the light reflected by a ring system with inner radius ri and outer radius ro is, in a simple approximation, given by the light reflected from a uniform inclined disk with radius ro subtracted by the light reflected by a similar uniform (and inclined) disk with a radius ri. This reflected signal also depends on the geometric albedo of the disk/ring system ( ) and on the tilt angle φ between the Earth-star-planet line and the plane of the rings at the moment of opposition. The lower the value of φ, the lower will be the “cross section” of the ring as seen by the star and by the observer. By definition, we have g(α) = 1 at the maximum phase angle. As such, the total planet-to-star flux ratio of a planet with a (optically thick) ring system can be approximated by
) and on the tilt angle φ between the Earth-star-planet line and the plane of the rings at the moment of opposition. The lower the value of φ, the lower will be the “cross section” of the ring as seen by the star and by the observer. By definition, we have g(α) = 1 at the maximum phase angle. As such, the total planet-to-star flux ratio of a planet with a (optically thick) ring system can be approximated by ![\begin{equation} \frac{F_{\rm planet+ring}}{F_{*}} = A_{\rm g} \left(\frac {R_{\rm p}}{a} \right)^{2} + A_{\rm g}^r g_{\rm r}(\phi) \left[\left(\frac {r_{\rm o}}{a} \right)^{2} - \left(\frac {r_{\rm i}}{a} \right)^{2} \right] \ , \label{eq:FluxesRatio} \end{equation}](/articles/aa/full_html/2015/11/aa26673-15/aa26673-15-eq17.png) (2)where gr(φ) ≈ sin2φ is a “reflectivity” function that depends on the tilt of the rings with respect to the line of sight (see Sect. 3.1). This model is very simplistic and only serves to understand whether a ring system can explain the observed signal.
(2)where gr(φ) ≈ sin2φ is a “reflectivity” function that depends on the tilt of the rings with respect to the line of sight (see Sect. 3.1). This model is very simplistic and only serves to understand whether a ring system can explain the observed signal.
To check that this configuration can explain the observed reflected light CCF of 51 Peg b, the first thing we need is to constrain the possible values for ri and ro (i.e., of the inner and outer radii of a possible ring system around 51 Peg b). Looking at the case of Saturn, we see that ri can be very close to the radius of the planet. We see no reason for this to be different in the case of 51 Peg b, so we thus consider that ri = Rp.
From a dynamical stability point of view, to constrain the outer radius ro we use the Hill approximation. The Hill radius is derived from 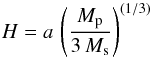 (3)where Mp and Ms are the planet and stellar masses, respectively. Assuming that the real mass of 51 Peg b is 0.46 MJup, that the mass of its host, 51 Peg, is 1.04 M⊙ (Santos et al. 2013), and that the orbital separation is 0.052 au (Martins et al. 2015), we then derive a value of H = 5.9 RJup. We should note, however, that several dynamical studies have pointed out that the outer edges of the Hill sphere are unstable (see discussion in Schlichting & Chang 2011; Kenworthy & Mamajek 2015). If we assume that only regions within 2/3 H are stable, then the outer edge of the ring system around 51 Peg b should be ~4 RJup.
(3)where Mp and Ms are the planet and stellar masses, respectively. Assuming that the real mass of 51 Peg b is 0.46 MJup, that the mass of its host, 51 Peg, is 1.04 M⊙ (Santos et al. 2013), and that the orbital separation is 0.052 au (Martins et al. 2015), we then derive a value of H = 5.9 RJup. We should note, however, that several dynamical studies have pointed out that the outer edges of the Hill sphere are unstable (see discussion in Schlichting & Chang 2011; Kenworthy & Mamajek 2015). If we assume that only regions within 2/3 H are stable, then the outer edge of the ring system around 51 Peg b should be ~4 RJup.
We note, however, that for radii higher than the Roche radius, we should expect that ring particles gather to form satellites. The Roche radius, below which a given satellite of density ρ will break up, can be derived from (e.g., de Pater & Lissauer 2010) 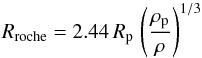 (4)where ρp is the density of the planet. Assuming that 51 Peg b has a radius of 1.2 RJup, we derive ρp = 0.6 g cm-3. Considering ρ = 3 g cm-3 (typical of rocks), this implies a Roche Radius of ~1.5 RJup. If we assume that beyond 2 Rroche there should no longer be any ring particles2, this would imply rout ~ 3.0 RJup, a value lower than the one found above when assuming the Hill radius.
(4)where ρp is the density of the planet. Assuming that 51 Peg b has a radius of 1.2 RJup, we derive ρp = 0.6 g cm-3. Considering ρ = 3 g cm-3 (typical of rocks), this implies a Roche Radius of ~1.5 RJup. If we assume that beyond 2 Rroche there should no longer be any ring particles2, this would imply rout ~ 3.0 RJup, a value lower than the one found above when assuming the Hill radius.
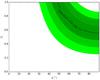 |
Fig. 1 Possible configurations of the inclination φ and |
In addition, these values for H and Rroche also depend on the real mass for the planet. The values above were computed assuming a mass of 0.46 MJup for 51 Peg b. This corresponds to an orbital inclination of 80 degrees. However, the inclination found in Martins et al. is affected by large error bars (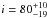 ). For instance, for values of i = 61 degrees (the lower bound), the real mass of 51 Peg b would be 0.53 MJup. This corresponds to a variation on the order of 10% in mass, a value that produces a minor effect in the derived H and Rroche.
). For instance, for values of i = 61 degrees (the lower bound), the real mass of 51 Peg b would be 0.53 MJup. This corresponds to a variation on the order of 10% in mass, a value that produces a minor effect in the derived H and Rroche.
Adopting values for ro = 3 and ri = 1 RJup, as derived above, we then estimate a rough value for the expected Fplanet + ring/F∗ from Eq. (2) (see Fig. 1). To do this, we also need to assume a value for Ag and 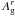 , as well as an inclination φ of the ring system with respect to the Earth-star-planet line. We should note that φ is at most equal to the inclination of the ring relative to the orbit and that this upper limit is only reached at equinox. Furthermore, this problem is highly degenerate. Different combinations of the albedos and inclinations will be able to replicate the observed (planet + rings)-to-star flux ratio.
, as well as an inclination φ of the ring system with respect to the Earth-star-planet line. We should note that φ is at most equal to the inclination of the ring relative to the orbit and that this upper limit is only reached at equinox. Furthermore, this problem is highly degenerate. Different combinations of the albedos and inclinations will be able to replicate the observed (planet + rings)-to-star flux ratio.
To keep the different parameters within physically realistic values, we decided to fix Ag to 0.3, a value that has been observed is several hot-Jupiters (e.g., Cowan & Agol 2011; Demory et al. 2013). As an example, using this value for Ag, φ = 60 degrees and a value of 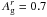 , we can explain the observed flux ratio (assuming ro and ri of 3 and 1 RJup, respectively).
, we can explain the observed flux ratio (assuming ro and ri of 3 and 1 RJup, respectively).
Increasing the inclination φ (i.e., increasing the angle between the rings and the Earth-star-planet line) would imply that the projected area of rings would also increase, and lower values of 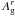 would be necessary to explain the signal. In Fig. 1 we show the values of the inclination φ against
would be necessary to explain the signal. In Fig. 1 we show the values of the inclination φ against 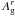 that satisfy the observed flux ratio. In the figure, the errors on the detected signal-to-star flux ratio were computed from error propagation from the recovered values of the signal’s amplitude and FWHM, i.e.,
that satisfy the observed flux ratio. In the figure, the errors on the detected signal-to-star flux ratio were computed from error propagation from the recovered values of the signal’s amplitude and FWHM, i.e., 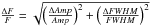 where F, Amp, and FWHM are the signal-to-star flux ratio, the amplitude, and FWHM of the detected signal, respectively. The errors in the stellar parameters were ignored because they are much smaller than the ones of the detected signal. Within the three-sigma error bars, possible solutions include pairs of φ and
where F, Amp, and FWHM are the signal-to-star flux ratio, the amplitude, and FWHM of the detected signal, respectively. The errors in the stellar parameters were ignored because they are much smaller than the ones of the detected signal. Within the three-sigma error bars, possible solutions include pairs of φ and 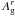 values as low as φ = 40 degrees and of the
values as low as φ = 40 degrees and of the 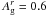 .
.
It is not simple to understand what could be reasonable values for 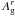 . Observations of Saturn’s rings are not much help in this case, since they are rich in ices. We found no discussion in the literature about the expected albedo for silicates and other refractory species at the equilibrium temperature of 51 Peg b, even if such species (e.g., SiO2) are able to condense at the equilibrium temperature of 51 Peg b (~1200 K – see Fig. 1 in Schlichting & Chang 2011). However, Draine (1985) computed values for the single scattering albedo of silicates in the interstellar medium that are as high as 0.8 at optical wavelengths. These values could be increased if significant backscattering occurs near opposition, as seen on Saturn’s rings and other solar system bodies (Hameen-Anttila & Pyykko 1972; Buratti et al. 1996; Verbiscer et al. 2005).
. Observations of Saturn’s rings are not much help in this case, since they are rich in ices. We found no discussion in the literature about the expected albedo for silicates and other refractory species at the equilibrium temperature of 51 Peg b, even if such species (e.g., SiO2) are able to condense at the equilibrium temperature of 51 Peg b (~1200 K – see Fig. 1 in Schlichting & Chang 2011). However, Draine (1985) computed values for the single scattering albedo of silicates in the interstellar medium that are as high as 0.8 at optical wavelengths. These values could be increased if significant backscattering occurs near opposition, as seen on Saturn’s rings and other solar system bodies (Hameen-Anttila & Pyykko 1972; Buratti et al. 1996; Verbiscer et al. 2005).
It is interesting to derive the expected ring rotational velocity and compare it to the value of the observed FWHM. Assuming Keplerian rotation3, the velocity of the rings should be 30 km s-1 at ri and 17 km s-1 at ro. This shows that the presence of rings should also significantly broaden the CCF of the planet, as observed. We should note, however, that the expected profile of the observed CCF may actually present two different components: one produced by the light reflected on the planet disk (that will have a FWHM similar to the stellar CCF if the planet rotates slowly) and the second produced by light reflected by the ring system, very likely with a broader CCF.
Schlichting & Chang (2011) also call attention to the possibility that the Poynting-Robertson drag slowly removes dust from a ring. As discussed in Burns (1984) and Sfair et al. (2009, and references therein), this effect implies that dust particles will remove orbital angular momentum and spiral into the planet. For a typical hot-Jupiter and assuming a ring orientation of 45 degrees with respect to the orbital plane, Schlichting & Chang (2011) computed ring lifetimes in the range of 107–108 years (see their Fig. 4). Assuming a lower inclination and a higher density optically thick ring, however, this lifetime will increase strongly. We thus see no strong reason for a ring system around 51 Peg b not to resist Poynting-Robertson drag. It is also worth noting that, as happens with Saturn, the presence of putative shepherd moons in the rings might greatly increase the lifetime of the rings; the presence of moons around hot-Jupiters is, however, questionable (Weidner & Horne 2010).
These numbers show that the observations reported in Martins et al. (2015) can in principle be explained if we assume that 51 Peg b has a ring system. We should note, however, that these estimates should be seen mostly as qualitative. Our major goal at this stage was to understand if the order of magnitude of the effect could be explained using the ring model. For instance, it would be relevant to understand if such a scenario should have been detected by existing phase curve observations using IR bands (Cowan et al. 2007). The large uncertainties in the observed CCF parameters, the properties of a ring system (albedos, inclinations), and in the properties of the atmosphere of 51 Peg b (e.g., the albedo and wind velocities) precludes any deeper insight into this issue.
3. Tilted rings?
In the previous section we assumed that a putative ring system around 51 Peg b could have any tilt angle, following the suggestion of Schlichting & Chang (2011). As can be seen in Fig. 1, this has a strong impact on our results. We therefore decided to verify this assumption.
The initial spin state of the planet is unknown. The rotation period is supposed to be short, but the obliquity (the angle between the equator and the orbital plane, here denoted by ε) can assume any value, due to large impacts and planet-planet scattering at early stages in the formation process (e.g., Dones & Tremaine 1993). However, due to the proximity of the star, the spin of hot-Jupiters slowly evolves until an equilibrium configuration is reached, corresponding to synchronous rotation and zero obliquity (e.g., Hut 1980). The typical time scale τ for reaching this final equilibrium is given by Correia (e.g., 2009)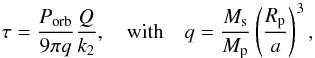 (5)where Porb is the orbital period, Q the dissipation quality factor, and k2 the second Love number for the potential. For Jupiter, astrometric observations provide Q/k2 ≈ 105 (Lainey et al. 2009). Adopting this same value for 51 Peg b gives τ ~ 105 yr, strongly suggesting that it has reached its final configuration for the spin. The same is true for all hot-Jupiters with a< 0.1 au. Values of Q as high as 107 have been proposed for stars (Penev et al. 2012), and this value could lead to τ ~ 108 yr if we assume k2 ~ 0.1, as expected for giant planets (Yoder 1995).
(5)where Porb is the orbital period, Q the dissipation quality factor, and k2 the second Love number for the potential. For Jupiter, astrometric observations provide Q/k2 ≈ 105 (Lainey et al. 2009). Adopting this same value for 51 Peg b gives τ ~ 105 yr, strongly suggesting that it has reached its final configuration for the spin. The same is true for all hot-Jupiters with a< 0.1 au. Values of Q as high as 107 have been proposed for stars (Penev et al. 2012), and this value could lead to τ ~ 108 yr if we assume k2 ~ 0.1, as expected for giant planets (Yoder 1995).
Ring systems are believed to have several possible origins: the result of impact events (e.g., Tiscareno 2013), captured objects or satellites that are tidally destroyed (e.g., Charnoz et al. 2009b; Canup 2010), or even remnants from planet formation (though this last hypothesis is less likely – Charnoz et al. 2009a). In all cases, they settle in a special plane around the planet, called the Laplacian plane (e.g., Lehébel & Tiscareno 2015). It is usually defined as the plane normal to the axis about which the pole of a satellite’s orbit precesses (Laplace 1805). For circular orbits, the dynamics of the rings’ particles is essentially governed by a single parameter, often called the Laplace radius (Tremaine et al. 2009) 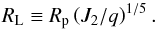 (6)For ro<RL, the rings can settle in the equatorial plane of the planet or in polar orbits. For ri>RL, the rings can only settle in the orbital plane of the system (implying φ = 0).For ri<RL<ro, we expect a transition between the different regimes, called “warped” ring.
(6)For ro<RL, the rings can settle in the equatorial plane of the planet or in polar orbits. For ri>RL, the rings can only settle in the orbital plane of the system (implying φ = 0).For ri<RL<ro, we expect a transition between the different regimes, called “warped” ring.
The parameter J2 is related to the flattening of the planet. For tidally evolved synchronous planets, we have (e.g., Correia & Rodríguez 2013) 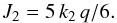 (7)For Jupiter-like planets k2 ≈ 1/2 (e.g., Yoder 1995). Using this value to compute the J2 gives RL = 0.84 Rp for the Laplace radius (Eq. (6)). We thus conclude that for any hot-Jupiter ri>RL, so ring systems can only be observed in the orbital plane (φ = 0).
(7)For Jupiter-like planets k2 ≈ 1/2 (e.g., Yoder 1995). Using this value to compute the J2 gives RL = 0.84 Rp for the Laplace radius (Eq. (6)). We thus conclude that for any hot-Jupiter ri>RL, so ring systems can only be observed in the orbital plane (φ = 0).
This result shows that “warped” rings are unlikely for close-in planets such as 51 Peg b, except if we assume that the system is young and not yet synchronous. For a coplanar ring system, however, according to the approximation presented in Eq. (2), we expect no reflected light at all. The approximation is thus no longer useful, though it hints that a ring configuration is likely not able to explain the reflected light signal as observed in Martins et al. (2015). It is, however, worth understanding what is the real amount of reflected light from a ring system in such a situation.
3.1. Reflectivity
In this section, we no longer assume that the Earth is aligned with the star-planet radius vector. It is then necessary to distinguish two inclination angles of the rings’ plane: the first one, denoted φi, is computed with respect to the direction of the star, while the second, φe, is given relative to the line of sight. We note that at conjunction, φe = φi = φ. For a distant star (point source), the flux Fr received by the rings depends only on the angle φi between the direction of the star and the rings’ plane. We thus have 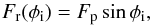 (8)where Fp is the flux that the ring would receive if it was perpendicular to the incident light. The amount of flux reflected by the ring in the direction of the observer also depends on the angle φe between the line of sight and the plane of the ring. If the scattering is isotropic, the reflectivity reads (see Appendix)
(8)where Fp is the flux that the ring would receive if it was perpendicular to the incident light. The amount of flux reflected by the ring in the direction of the observer also depends on the angle φe between the line of sight and the plane of the ring. If the scattering is isotropic, the reflectivity reads (see Appendix) 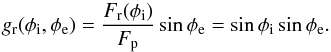 (9)In the approximation φi = φe = φ, as in the previous section, we recover the dependency in sin2φ. If a ring system around 51 Peg b needs to be coplanar with the orbital plane, then sin2φ = 0, and the reflected light flux is thus only due to the light reflected by the planet (Eq. (2) and Fig. 3). However, for hot-Jupiters, the star cannot be seen as a point source, since the planet is close enough to receive light coming from the fraction of the stellar disk that illuminates the rings. It is thus interesting to estimate the total illumination, i.e., a more general expression for Fr(φ), and try to understand if this could actually be responsible for the observed signal.
(9)In the approximation φi = φe = φ, as in the previous section, we recover the dependency in sin2φ. If a ring system around 51 Peg b needs to be coplanar with the orbital plane, then sin2φ = 0, and the reflected light flux is thus only due to the light reflected by the planet (Eq. (2) and Fig. 3). However, for hot-Jupiters, the star cannot be seen as a point source, since the planet is close enough to receive light coming from the fraction of the stellar disk that illuminates the rings. It is thus interesting to estimate the total illumination, i.e., a more general expression for Fr(φ), and try to understand if this could actually be responsible for the observed signal.
 |
Fig. 2 Geometry of a system containing a hot-Jupiter with rings. uz is the unit vector along the radius vector of the planet relative to the star, ux is perpendicular to uz in the plane defined by uz and k (ux is not necessarily the normal of the orbit). uy complete the orthonormal base frame (ux,uy,uz). |
We let Is be the intensity emitted by the stellar surface and we assume that it is uniform, i.e., we neglect the limb-darkening. Then, the energy received by a ring element of surface dA is given by 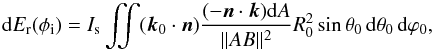 (10)where the double integral is computed over the portion of the stellar surface visible from a ring element. In this expression, k0 is the normal of the surface of the star at a given point A of spherical coordinates (R0,ϕ0,θ0), B is a point of the ring, and n the unit vector along AB (see Fig. 2). For 51 Peg b we have a = 11 R0, so we assume that a ≫ R0. Moreover, as an order of magnitude, we only compute the incoming energy at the center B of the ring. The flux received by an element of the ring is then defined as
(10)where the double integral is computed over the portion of the stellar surface visible from a ring element. In this expression, k0 is the normal of the surface of the star at a given point A of spherical coordinates (R0,ϕ0,θ0), B is a point of the ring, and n the unit vector along AB (see Fig. 2). For 51 Peg b we have a = 11 R0, so we assume that a ≫ R0. Moreover, as an order of magnitude, we only compute the incoming energy at the center B of the ring. The flux received by an element of the ring is then defined as 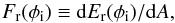 (11)and Fp is equal to πIs(R0/a)2. To compute the integral (10), we consider two cases. If the ring’s inclination φi is greater than the angular radius of the star , each element of the ring gets the light from the full stellar disk:
(11)and Fp is equal to πIs(R0/a)2. To compute the integral (10), we consider two cases. If the ring’s inclination φi is greater than the angular radius of the star , each element of the ring gets the light from the full stellar disk: 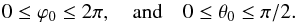 (12)In that case, at third order in R0/a, the reflectivity of the ring is still given by gr(φi,φe) = sinφisinφe (see Appendix).
(12)In that case, at third order in R0/a, the reflectivity of the ring is still given by gr(φi,φe) = sinφisinφe (see Appendix).
 |
Fig. 3 Flux received by the ring as a function of the tilt angle. |
On the other hand, if the inclination φi of the ring is less than φc, a part of the stellar disk is occulted. In that case, the reflectivity becomes (see Appendix) ![\begin{eqnarray} g_{\rm r}(\phi_{\rm i}) &=& \frac{\sin\phi_{\rm e}}{\pi} \bigg\{ \left(\frac{\pi}{2}+\varphi_a\right)\sin\phi_{\rm i} + \frac{2R_0}{3a}\cos\phi_{\rm i}\cos^3\varphi_a \nonumber \\ && + \cos\varphi_a \sin\phi_{\rm i} \bigg[\sin\varphi_a - \frac{\pi}{2} \cos\varphi_a \sin\phi_{\rm i} \nonumber \\ && + \frac{R_0}{a} \left(\pi \sin\varphi_a - \frac{8}{3}\cos\varphi_a\sin\phi_{\rm i}\right) \cos\varphi_a\cos\phi_{\rm i} \bigg]\bigg\} , \end{eqnarray}](/articles/aa/full_html/2015/11/aa26673-15/aa26673-15-eq106.png) (13)where ϕa is defined as
(13)where ϕa is defined as 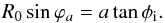 (14)In particular, for small tilt angle (φi ≪ R0/a), we get
(14)In particular, for small tilt angle (φi ≪ R0/a), we get 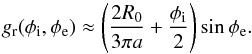 (15)For 51 Peg, in the limit of small tilt angles, gr ≈ 0.02sinφe, that is, the rings only receive about 2% of the maximal flux computed at φi = 90°. This value is far too small to explain the observed signal as derived in Sect. 2.
(15)For 51 Peg, in the limit of small tilt angles, gr ≈ 0.02sinφe, that is, the rings only receive about 2% of the maximal flux computed at φi = 90°. This value is far too small to explain the observed signal as derived in Sect. 2.
4. Rings from transit surveys
Even though the results presented above do not support the ring hypothesis to explain the signal observed in 51 Peg b, the dynamical discussions presented also show that coplanar rings could be present around hot-Jupiters. One can thus wonder if rings are actually a frequent phenomenon around these sort of planets.
In a recent paper, Kenworthy & Mamajek (2015) found evidence that the young pre-main-sequence star J1407 (1SWASP J140747.93−394542.6 J1407) may have a planet with a massive ring system. This case is not fully comparable to 51 Peg b, in the sense that our target is much older and has a much shorter orbital period. However, this example shows that present-day photometry is able to detect the presence of rings around exoplanets.
 |
Fig. 4 Transit depth, duration signal, and derived stellar mean density for a transiting planet+ring system as a function of the impact parameter as computed using SOAP-T+R and EXORING. |
This issue has also been discussed from a modeling point of view (Arnold & Schneider 2004; Barnes & Fortney 2004; Dyudina et al. 2005; Ohta et al. 2009; Tusnski & Valio 2014). In particular, simulations have shown that if massive rings are present in hot-Jupiters, the precision of transit surveys like Kepler would have already allowed them to be detected. The question is then to understand if we have actually already detected rings photometrically but their existence passed unnoticed.
In a recent paper, Zuluaga et al. (2015) have shown that the presence of rings would produce (at least) two different effects. One of these is that ringed planets would imply that the value of the stellar surface gravity (or stellar density) derived from the light curve would be systematically smaller than the one observed using asteroseismology, for example. Indeed, and although other parameters may be responsible for the derivation of erroneous values of the stellar density from the transit light curve (Kipping 2014), such a trend is expected if rings (even if not very massive/wide) are common around short-period exoplanets.
The other effect discussed in Zuluaga et al. (2015) is more “obvious”: a ringed planet would trigger changes in the transit light curve (with respect to a simple planet). In particular, transits should be deeper and longer. If the large rings are present, the amplitude of the transiting signal could even be similar to the one expected for an eclipsing binary star.
To test these scenarios we modified the SOAP-T tool (Oshagh et al. 2013) in order to add a planetary ring to the transiting planet (hereafter we call this code SOAP-T+R). SOAP-T was originally designed to generate the radial velocity variations and light curves for systems consisting of a rotating spotted star with a transiting planet. The model assumes that the rings are uniform and completely opaque and that they have an orientation with respect to the orbital plane. By comparing the transit light curves of SOAP-T+R with those of SOAP-T, we are able to recognize the impact of rings on the transit light curves. A full description of this code is beyond the scope of the present paper.
 |
Fig. 5 Synthetic light curves simulating the light curves of transiting planets with (right) and without rings (left). The parameters of each planet are denoted in the inset. Dots correspond to data binned with a 30-min cadence similar to long cadence of Kepler. Different system inclinations are used. In all the simulations, the ring is considered to be coplanar with the orbital plane. |
To check that the SOAP-T+R code was working properly, we compared its results with the ones obtained with the available EXORING code (Zuluaga et al. 2015). The obtained transit duration and depth are shown in Fig. 4 as simulated using both codes as functions of the impact parameter for a ring system that is coplanar with the orbital plane. The comparison of the results obtained using SOAP-T+R and EXORING for the transit duration show very good agreement. On the other hand, the transit depth obtained from SOAP-T+R displays deeper transits than those using EXORING. This difference is explained by the fact that the stellar limb darkening is neglected in the EXORING code, while in SOAP-T+R we consider a quadratic limb darkening coefficient close to the solar value. Indeed, if we assume no limb darkening in SOAP-T+R, we obtain the same results as EXORING (see also Fig. 4).
In Fig. 5 we show the results of our simulations after comparing the transit light curves produced by a planet (left) and by a planet with rings (right). Here we assume a ring system that is coplanar with the orbital plane and that has inner and outer radii of 1 and 4 RJup, respectively. Quadratic limb darkening parameters u1 = 0.29 and u2 = 0.34 were used in this simulation (as expected for a Sun-like star). As seen in the figure, the impact of such a ring system can be quite significant. The most interesting result is that the shape of transit light curves of ringed planets (deep transit, long duration, and shape – in most cases “V” shaped) look very much like the eclipse light curve of one eclipsing binary. Therefore, possible transiting planets with rings could have been observed by transit surveys, such as Kepler and CoRoT, however they could have easily been misclassified as false positive candidates.
We need to add, however, that the actual capability to distinguish between an eclipsing binary and a transiting ringed planet needs to be assessed by, for example, simulating the expected light curves in detail (including the different sources of noise) and investigating the residuals when fitting both models to the simulated data. We leave this detailed analysis to future studies.
The lower panel of Fig. 4 presents the impact of the “unaccounted” effect of a ringed planet on the derived stellar density as a function of planet impact parameter. To estimate this we used the stellar density as derived using the Eq. (9) in Seager & Mallén-Ornelas (2003). The plot shows that the stellar density is underestimated as we move toward higher impact parameter values. In this respect it is interesting to note that Huber et al. (2013) find that the difference between the light-curve stellar density and the value derived using asteroseismology is a function of the impact parameter of the planet. We are not advocating, however, that rings are the definite explanation for this trend. In any case, most of the systems in the Huber et al. paper are low-mass, small-radius, and not Jovian in nature.
5. Conclusions
In this paper we have explored the possibility that the reflected light spectrum observations of 51 Peg b (Martins et al. 2015) can be explained if we assume that this hot-Jupiter has a ring system. Using a simple model we showed that, overall, the observed signal can indeed be explained by a ring system under the assumption that rings are tilted with respect to the orbital plane of the planet. We showed, however, that dynamical arguments suggest that in any synchronous hot-Jupiter like (we expect) 51 Peg b, this configuration is unlikely. In the case of a ring system coplanar with the orbital plane of the planet, we also showed that the total amount of incident flux is about two orders of magnitude smaller than the one needed to explain the observations.
The study shows, however, that the analysis of the reflected light spectrum from an exoplanet could be a very interesting method of detecting rings around short-period systems, in particular those not transiting. This approach can also complement the measurement of brightness variations along a phase curve, as already proposed by Dyudina et al. (2005). Observations of apparently high-albedo planets that present broadened spectral lines or line profiles showing two different components (see Sect. 2) could hint at the presence of rings around other planets. A detailed model of the observed line-shapes could indeed provide relevant information about the system.
We also discussed the possibility that planets with rings could have been detected by space missions like Kepler but simply discarded as binaries owing to the shape and depth of the transiting signal. In this respect we propose that it would be interesting to obtain precise radial velocity measurements of candidate binary stars from the Kepler field, in order to derive the masses of the companions. The study of the light curves to search for transiting secondary binary like-signals with no signature of secondary eclipses or beaming and ellipsoidal effects (Mazeh et al. 2012) could also help to select the best candidates. We note that smaller ring systems could also be responsible for slightly deeper transits, leading to deriving an inflated radius for the transiting planet. A careful analysis of the data could be relevant in such cases.
Online material
Appendix A: Flux received by the ring
Here, we detail the computation of the flux Fr(φi) received by the ring per unit area. The notation is the same as in Sect. 3.1 of the main text (see also Fig. 2). The general expression of the flux derived from Eqs. (10) and (11) is 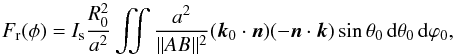 (A.1)where
(A.1)where  (A.2)The integrand in the expression of Fr is of order unity. We expand it at the first order in R0/a ≪ 1. We get
(A.2)The integrand in the expression of Fr is of order unity. We expand it at the first order in R0/a ≪ 1. We get ![\appendix \setcounter{section}{1} \begin{eqnarray} F_{\rm r} &=& I_{\rm s} \frac{R_0^2}{a^2} \iint \bigg( \sin\phi_{\rm i}\cos\theta_0 +\frac{R_0}{a}\Big[\sin\phi_{\rm i} \left(3\cos^2\theta_0-1\right) \nonumber \\ && + \cos\phi_{\rm i}\sin\theta_0\cos\theta_0\cos\varphi_0 \Big] \bigg)\sin\theta_0 \,{\rm d}\theta_0 \,{\rm d}\varphi_0 . \label{eq.flux_integ} \end{eqnarray}](/articles/aa/full_html/2015/11/aa26673-15/aa26673-15-eq121.png) (A.3)We consider the most general case where each element of the ring only sees a fraction of the stellar disk (see Fig. A.1). This case happens when the tilt angle φi is less than the angular radius of the star . In this configuration, the visible surface is delimited by two curves: the arc CDE in the xy-plane of the star and bounded by −π/ 2−ϕa ≤ ϕ0 ≤ π/ 2 + ϕa, and the arc EC, which is half of a circle of radius R0cosϕa in the plane of the ring. For commodity, we recall the definition of the angle ϕa given in Eq. (14)
(A.3)We consider the most general case where each element of the ring only sees a fraction of the stellar disk (see Fig. A.1). This case happens when the tilt angle φi is less than the angular radius of the star . In this configuration, the visible surface is delimited by two curves: the arc CDE in the xy-plane of the star and bounded by −π/ 2−ϕa ≤ ϕ0 ≤ π/ 2 + ϕa, and the arc EC, which is half of a circle of radius R0cosϕa in the plane of the ring. For commodity, we recall the definition of the angle ϕa given in Eq. (14) 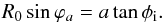 To compute the surface integral (A.3), we make use of the Stockes theorem that transforms a surface integral over Σ into a closed integral over its boundary ∂Σ as
To compute the surface integral (A.3), we make use of the Stockes theorem that transforms a surface integral over Σ into a closed integral over its boundary ∂Σ as 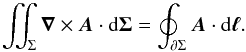 (A.4)For this problem, we set
(A.4)For this problem, we set 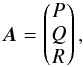 (A.5)where
(A.5)where ![\appendix \setcounter{section}{1} \begin{eqnarray} P &=& -\frac{1}{2} y \sin \phi_{\rm i} + \frac{R_0}{a}(-yz\sin\phi_{\rm i}-xy\cos\phi_{\rm i}) , \nonumber \\[2mm] Q &=& \frac{1}{2} x \sin \phi_{\rm i} + \frac{R_0}{a} xz\sin\phi_{\rm i} , \\ R &=& 0 . \nonumber \end{eqnarray}](/articles/aa/full_html/2015/11/aa26673-15/aa26673-15-eq132.png) (A.6)
(A.6)
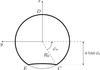 |
Fig. A.1 Area enclosed by the thick curve CDEC is the visible part of the star seen from an element of the ring. |
For the line integral CDE, we use r = (x,y,z) with 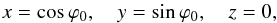 (A.7)where ϕ0 goes from (− π/ 2−ϕa) to (π/ 2 + ϕa),. While for the line integral EC, we set r = (x,y,z) with
(A.7)where ϕ0 goes from (− π/ 2−ϕa) to (π/ 2 + ϕa),. While for the line integral EC, we set r = (x,y,z) with ![\appendix \setcounter{section}{1} \begin{eqnarray} && x = \cos\varphi_a\sin\phi_{\rm i}\sin\psi-\sin\varphi_a , \nonumber \\[2mm] && y = \cos\varphi_a\cos\psi , \nonumber\\[2mm] && z = \cos\varphi_a\cos\phi_{\rm i}\sin\psi , \end{eqnarray}](/articles/aa/full_html/2015/11/aa26673-15/aa26673-15-eq139.png) (A.8)where ψ ranges from 0 to π. As a result, we get
(A.8)where ψ ranges from 0 to π. As a result, we get ![\appendix \setcounter{section}{1} \begin{eqnarray} F_{\rm r}(\phi_{\rm i}) &=& I_{\rm s} \frac{R_0^2}{a^2} \bigg\{ \left(\frac{\pi}{2}+\varphi_a\right)\sin\phi_{\rm i} + \frac{2R_0}{3a}\cos\phi_{\rm i}\cos^3\varphi_a \nonumber \\[2mm] & &+ \cos\varphi_a \sin\phi_{\rm i} \bigg[\sin\varphi_a - \frac{\pi}{2} \cos\varphi_a \sin\phi_{\rm i} \nonumber \\[2mm] && + \frac{R_0}{a} \left(\pi \sin\varphi_a - \frac{8}{3}\cos\varphi_a\sin\phi_{\rm i}\right) \cos\varphi_a\cos\phi_{\rm i} \bigg]\bigg\} . \label{eq.Fr_final} \end{eqnarray}](/articles/aa/full_html/2015/11/aa26673-15/aa26673-15-eq142.png) (A.9)In the case where φi>φc, Eq. (A.9) still holds if we set ϕa = π/ 2 so we get
(A.9)In the case where φi>φc, Eq. (A.9) still holds if we set ϕa = π/ 2 so we get 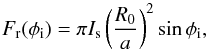 while for φi ≪ φc, ϕa ~ aφi/R0 and
while for φi ≪ φc, ϕa ~ aφi/R0 and 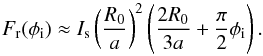
Appendix B: Reflectivity
The reflectivity of the ring is computed by assuming an isotropic scattering. Furthermore, it is assumed that given an incoming flux Fr, only a fraction 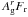 is re-emitted in the visible spectrum. Thus, the luminous intensity Ir of the rings is uniform and such that
is re-emitted in the visible spectrum. Thus, the luminous intensity Ir of the rings is uniform and such that 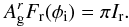 (B.1)Besides this, the flux received on Earth from the disk is
(B.1)Besides this, the flux received on Earth from the disk is 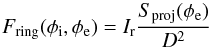 (B.2)where the ratio of the projected surface Sproj of the rings on the plane of the sky divided by the square of the distance D to the Earth represents the solid angle under which the rings are seen. As a result, we get
(B.2)where the ratio of the projected surface Sproj of the rings on the plane of the sky divided by the square of the distance D to the Earth represents the solid angle under which the rings are seen. As a result, we get 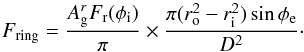 (B.3)Moreover, the stellar flux F⋆ received on Earth is
(B.3)Moreover, the stellar flux F⋆ received on Earth is 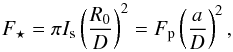 (B.4)
(B.4)
where we used Fp = πIs(R0/a)2. Combining Eqs. (B.3) and (B.4), we get ![\appendix \setcounter{section}{2} \begin{equation} \frac{F_\mathrm{ring}}{F_\star} = A_{\rm g}^r \, g_{\rm r}(\phi_{\rm i}, \phi_{\rm e}) \left[\left(\frac{r_{\rm o}}{a}\right)^2 - \left(\frac{r_{\rm i}}{a}\right)^2\right] , \end{equation}](/articles/aa/full_html/2015/11/aa26673-15/aa26673-15-eq159.png) (B.5)with gr a function representing the reflectivity of the rings given by
(B.5)with gr a function representing the reflectivity of the rings given by 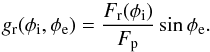 (B.6)
(B.6)
The rings of Saturn extend beyond the Roche limit, in particular the E ring, though they are essentially composed of micron and submicron particles (Hedman et al. 2012).
Acknowledgments
We would like to thank our referees, Dr. Sébastien Charnoz and the second anonymous referee, for the comments and suggestions that helped us to improve the quality of the paper. This work was supported by Fundação para a Ciência e a Tecnologia (FCT) through the research grant UID/FIS/04434/2013. P.F., N.C.S., and S.G.S. also acknowledge the support from FCT through Investigador FCT contracts of reference IF/01037/2013, IF/00169/2012, and IF/00028/2014, respectively, and POPH/FSE (EC) by FEDER funding through the program “Programa Operacional de Factores de Competitividade – COMPETE”. A.C. acknowledges support from CIDMA strategic project UID/MAT/04106/2013. P.F. further acknowledges support from Fundação para a Ciência e a Tecnologia (FCT) in the form of an exploratory project of reference IF/01037/2013CP1191/CT0001. A.S. is supported by the European Union under a Marie Curie Intra-European Fellowship for Career Development with reference FP7-PEOPLE-2013-IEF, number 627202. This work results within the collaboration of the COST Action TD 1308.
References
- Angerhausen, D., DeLarme, E., & Morse, J. A. 2014, PASP, submitted [arXiv:1404.4348] [Google Scholar]
- Arnold, L., & Schneider, J. 2004, A&A, 420, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, J. W., & Fortney, J. J. 2004, ApJ, 616, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Birkby, J. L., de Kok, R. J., Brogi, M., et al. 2013, MNRAS, 436, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Brogi, M., Snellen, I. A. G., de Kok, R. J., et al. 2013, ApJ, 767, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Buratti, B. J., Hillier, J. K., & Wang, M. 1996, Icarus, 124, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. A. 1984, Adv. Space Res., 4, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A. S. 2014, Nature, 513, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Canup, R. M. 2010, Nature, 468, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Charnoz, S., Dones, L., Esposito, L. W., Estrada, P. R., & Hedman, M. M. 2009a, Origin and Evolution of Saturn’s Ring System, eds. M. K. Dougherty, L. W. Esposito, & S. M. Krimigis, 537 [Google Scholar]
- Charnoz, S., Morbidelli, A., Dones, L., & Salmon, J. 2009b, Icarus, 199, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M. 2009, ApJ, 704, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., & Rodríguez, A. 2013, ApJ, 767, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., Agol, E., & Charbonneau, D. 2007, MNRAS, 379, 641 [NASA ADS] [CrossRef] [Google Scholar]
- de Pater, I., & Lissauer, J. J. 2010, Planetary Sciences (Cambridge University Press) [Google Scholar]
- Deming, D., Seager, S., Richardson, L. J., & Harrington, J. 2005, Nature, 434, 740 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Demory, B.-O., Gillon, M., Seager, S., et al. 2012, ApJ, 751, L28 [Google Scholar]
- Demory, B.-O., de Wit, J., Lewis, N., et al. 2013, ApJ, 776, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Dones, L., & Tremaine, S. 1993, Icarus, 103, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1985, ApJS, 57, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Dyudina, U. A., Sackett, P. D., Bayliss, D. D. R., et al. 2005, ApJ, 618, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Hameen-Anttila, K. A., & Pyykko, S. 1972, A&A, 19, 235 [NASA ADS] [Google Scholar]
- Hedman, M. M., Burns, J. A., Hamilton, D. P., & Showalter, M. R. 2012, Icarus, 217, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Chaplin, W. J., Christensen-Dalsgaard, J., et al. 2013, ApJ, 767, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1980, A&A, 92, 167 [NASA ADS] [Google Scholar]
- Kenworthy, M. A., & Mamajek, E. E. 2015, ApJ, 800, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2014, MNRAS, 440, 2164 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lainey, V., Arlot, J.-E., Karatekin, Ö., & van Hoolst, T. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Laplace, P. S. 1805, Traité de Mécanique céleste, Vol. 4 (Paris: Gauthier-Villars) [Google Scholar]
- Lehébel, A., & Tiscareno, M. S. 2015, A&A, 576, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madhusudhan, N., Crouzet, N., McCullough, P. R., Deming, D., & Hedges, C. 2014, ApJ, 791, L9 [Google Scholar]
- Martins, J. H. C., Santos, N. C., Figueira, P., et al. 2015, A&A, 576, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mazeh, T., Nachmani, G., Sokol, G., Faigler, S., & Zucker, S. 2012, A&A, 541, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohta, Y., Taruya, A., & Suto, Y. 2009, ApJ, 690, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Oshagh, M., Boisse, I., Boué, G., et al. 2013, A&A, 549, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Penev, K., Jackson, B., Spada, F., & Thom, N. 2012, ApJ, 751, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlichting, H. E., & Chang, P. 2011, ApJ, 734, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S. 2010, Exoplanet Atmospheres: Physical Processes (Princeton University Press) [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Sfair, R., Winter, S. M. G., Mourão, D. C., & Winter, O. C. 2009, MNRAS, 395, 2157 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stevenson, K. B., Désert, J.-M., Line, M. R., et al. 2014, Science, 346, 838 [NASA ADS] [CrossRef] [Google Scholar]
- Tiscareno, M. S. 2013, in Planetary Rings, eds. T. D. Oswalt, L. M. French, & P. Kalas, 309 [Google Scholar]
- Tremaine, S., Touma, J., & Namouni, F. 2009, AJ, 137, 3706 [NASA ADS] [CrossRef] [Google Scholar]
- Tusnski, L. R. M., & Valio, A. 2014, in IAU Symp. 293, ed. N. Haghighipour, 168 [Google Scholar]
- Verbiscer, A. J., French, R. G., & McGhee, C. A. 2005, Icarus, 173, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J.-M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Weidner, C., & Horne, K. 2010, A&A, 521, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. 2015, A&A, 577, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoder, C. F. 1995, in Global Earth Physics: A Handbook of Physical Constants (Washington D.C: American Geophysical Union), 1 [Google Scholar]
- Zuluaga, J. I., Kipping, D., Sucerquia, M., & Alvarado, J. A. 2015, ApJ, 803, L14 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Possible configurations of the inclination φ and |
| In the text | |
 |
Fig. 2 Geometry of a system containing a hot-Jupiter with rings. uz is the unit vector along the radius vector of the planet relative to the star, ux is perpendicular to uz in the plane defined by uz and k (ux is not necessarily the normal of the orbit). uy complete the orthonormal base frame (ux,uy,uz). |
| In the text | |
 |
Fig. 3 Flux received by the ring as a function of the tilt angle. |
| In the text | |
 |
Fig. 4 Transit depth, duration signal, and derived stellar mean density for a transiting planet+ring system as a function of the impact parameter as computed using SOAP-T+R and EXORING. |
| In the text | |
 |
Fig. 5 Synthetic light curves simulating the light curves of transiting planets with (right) and without rings (left). The parameters of each planet are denoted in the inset. Dots correspond to data binned with a 30-min cadence similar to long cadence of Kepler. Different system inclinations are used. In all the simulations, the ring is considered to be coplanar with the orbital plane. |
| In the text | |
 |
Fig. A.1 Area enclosed by the thick curve CDEC is the visible part of the star seen from an element of the ring. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.