| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 7 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201526366 | |
| Published online | 06 July 2015 | |
Online material
Detailed abundances.
Variations in stellar parameters for different assumptions on Teff, log g, and microturbulent velocity.
 |
Fig. 4
Colour image created from DES, g,r,i images showing the location of the two target stars. |
| Open with DEXTER | |
 |
Fig. 5
Updated version of Fig. 7 of de Jong et al. (2010). The radial velocity (lower panel), distance (middle panel), and sky position (upper panel) of Crater (shown as a star) compared to those of Leo IV (empty dot) and Leo V (filled dot). The lines are the orbits for Leo IV and Leo V, computed by de Jong et al. (2010), assuming common energy and angular momentum for the two galaxies, using Leo IV and Leo V (dotted line) as initial conditions, or their mean properties (dashed line), respectively. |
| Open with DEXTER | |
Appendix A: Lower limit to the radial velocity dispersion
The difference of two normal random variables with means μ1,μ2), and standard deviations σ1,σ2 follows a normal distribution, with ![]() and mean μ1−μ2. Assuming that the velocity distribution is normal and ignoring the measurement errors, the velocity difference between two stars is expected to be normally distributed with a mean of 0 km s-1 and a standard deviation of
and mean μ1−μ2. Assuming that the velocity distribution is normal and ignoring the measurement errors, the velocity difference between two stars is expected to be normally distributed with a mean of 0 km s-1 and a standard deviation of ![]() , where σv is the standard deviation of the original distribution. Using the table on p. 253 of Bevington & Robinson (1992), which provides the integral of a Gaussian distribution, we derive that the integral between −1.96 ≤ z ≤ + 1.96 is 0.95, where
, where σv is the standard deviation of the original distribution. Using the table on p. 253 of Bevington & Robinson (1992), which provides the integral of a Gaussian distribution, we derive that the integral between −1.96 ≤ z ≤ + 1.96 is 0.95, where ![]() and μ is the mean. In our case, x = 10.2km s-1, μ = 0 km s-1 and
and μ is the mean. In our case, x = 10.2km s-1, μ = 0 km s-1 and ![]() ; this implies that z = 1.96 corresponds σv = 3.7km s-1. In other words, there is a 95% probability that the parent velocity distribution has a σ> 3.7km s-1. If we take into account the errors, no conclusion can be reached because the measured radial velocities of the two stars are also consistent with a zero radial velocity dispersion.
; this implies that z = 1.96 corresponds σv = 3.7km s-1. In other words, there is a 95% probability that the parent velocity distribution has a σ> 3.7km s-1. If we take into account the errors, no conclusion can be reached because the measured radial velocities of the two stars are also consistent with a zero radial velocity dispersion.
Appendix B: Lower limit to the dynamical mass of Crater
To derive a lower limit, we assumed that Crater and the globular cluster 47 Tuc are in dynamical equilibrium and that the virial theorem applies. For this system, the mass, M, can be expressed in terms of its velocity dispersion, σ, and exponential radius, rh (see e.g. Spitzer 1987) : 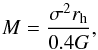 (B.1)where G is the gravitational constant. We thus may write
(B.1)where G is the gravitational constant. We thus may write 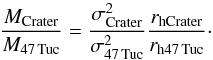 (B.2)Because we only have a lower limit for σCrater, this becomes
(B.2)Because we only have a lower limit for σCrater, this becomes 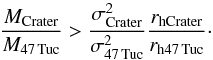 (B.3)We assumed for Crater σCrater> 3.7km s-1, rhCrater = 0.47′ (Laevens et al. 2014) or rhCrater = 0.6′ (Belokurov et al. 2014) and a distance of 145 kpc (Laevens et al. 2014). For 47 Tuc we assumed σ47 Tuc = 7km s-1 a median value from Kučinskas et al. (2014), rh47 Tuc = 174′′ (Trager et al. 1993), and a distance of 4.5 kpc (Harris 2010).
(B.3)We assumed for Crater σCrater> 3.7km s-1, rhCrater = 0.47′ (Laevens et al. 2014) or rhCrater = 0.6′ (Belokurov et al. 2014) and a distance of 145 kpc (Laevens et al. 2014). For 47 Tuc we assumed σ47 Tuc = 7km s-1 a median value from Kučinskas et al. (2014), rh47 Tuc = 174′′ (Trager et al. 1993), and a distance of 4.5 kpc (Harris 2010).
With these values, we obtain ![]() for the radius measured by Laevens et al. (2014) and
for the radius measured by Laevens et al. (2014) and ![]() for the radius measured by Belokurov et al. (2014). Either way, it is clear that Crater is more massive (dynamically) than 47 Tuc. Even disregarding the velocity dispersions, it might have been suspected that this is the case because the radius of Crater is larger than that of 47 Tuc. Of course, if Crater is not in dynamical equlibrium, this reasoning does not hold.
for the radius measured by Belokurov et al. (2014). Either way, it is clear that Crater is more massive (dynamically) than 47 Tuc. Even disregarding the velocity dispersions, it might have been suspected that this is the case because the radius of Crater is larger than that of 47 Tuc. Of course, if Crater is not in dynamical equlibrium, this reasoning does not hold.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


