| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201424992 | |
| Published online | 19 June 2015 | |
Online material
Appendix A: Transits and observation gaps
When planet transits and reflected light curves are observed in one signal, large amplitudes from the periodic transits are added on top of the weak reflection peaks. For Jupiters near dwarf stars, it may still be possible to separate the two components in the signal.
Observing from direction ![]() , one sees a planet passing in front of the star disk for
, one sees a planet passing in front of the star disk for ![]() . The transits are thus found (taking φ = 0 for convenience, and r ≪ S, and
. The transits are thus found (taking φ = 0 for convenience, and r ≪ S, and ![]() ) in t-intervals for which
) in t-intervals for which ![]() Then the measured signal dips by − s2I0/S2 (which is − 10-4I0 for a twin earth). We are interested in the reflected signal from a planet. This is a factor S2/ 4r2 weaker (10-6) than a transit signal and s2/ 4r2 weaker (10-10) than the star. For a Jupiter close to a dwarf star, these ratios are much more practical than for an Earth-twin, and it may not be necessary to block the star.
Then the measured signal dips by − s2I0/S2 (which is − 10-4I0 for a twin earth). We are interested in the reflected signal from a planet. This is a factor S2/ 4r2 weaker (10-6) than a transit signal and s2/ 4r2 weaker (10-10) than the star. For a Jupiter close to a dwarf star, these ratios are much more practical than for an Earth-twin, and it may not be necessary to block the star.
Although the transit signal is of short duration (minutes), the combined signal can be detected continuously (for years). Consider the Fourier series of a rapid transit: 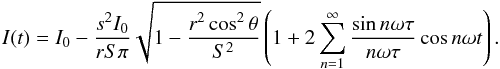 (A.1)The short duration of the eclipse gives rise to peak amplitudes of a fraction s2/rS of I0 (of the order 10-7I0). The Fourier coefficients of the transit signal are
(A.1)The short duration of the eclipse gives rise to peak amplitudes of a fraction s2/rS of I0 (of the order 10-7I0). The Fourier coefficients of the transit signal are 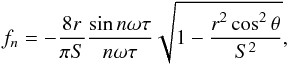 (A.2)which are of the order r/S compared to the coefficients in the phase signal, which are of order 1. In other words, in the Fourier spectrum, the reflected signal is about a factor S/r weaker (10-3) than the transit signal. To observe the phase part in a combined phase-plus-transit signal, the noise from the transit must be less than the phase peak amplitudes. Our Sun has noise levels of 10-5 at (transit-frequencies of) 10-5 Hz, and a noise level 10-3 for (orbital frequencies) 10-6 Hz, see Aigrain et al. (2004), so the large transit component does indeed pose a problem since the absolute noise will be large. Of course, when a planet is periodically blocking its star, the star is also blocking the planet every other half period. The corresponding dip in the signal is again a factor S/r smaller.
(A.2)which are of the order r/S compared to the coefficients in the phase signal, which are of order 1. In other words, in the Fourier spectrum, the reflected signal is about a factor S/r weaker (10-3) than the transit signal. To observe the phase part in a combined phase-plus-transit signal, the noise from the transit must be less than the phase peak amplitudes. Our Sun has noise levels of 10-5 at (transit-frequencies of) 10-5 Hz, and a noise level 10-3 for (orbital frequencies) 10-6 Hz, see Aigrain et al. (2004), so the large transit component does indeed pose a problem since the absolute noise will be large. Of course, when a planet is periodically blocking its star, the star is also blocking the planet every other half period. The corresponding dip in the signal is again a factor S/r smaller.
The effect of discontinuous but periodic observation gaps on the Fourier peaks is different from that of a transit. For observation gaps, the continuous signal is multiplied with a periodic function, which is zero for the intervals sin | ωt | < sinωτ, whereas for a transit, such a function is added instead. Periodic interruptions at the inferior and major conjunction are inevitable for an edge-on observation, when the planet passes behind an occulter or within the telescope’s inner working angle. The blocking durations 2τ must obviously be short (compared to the period). In the short-gaps limit, the multiplicative function becomes 1−2ωτ ∑ e2inωt/π. The even and odd peaks, f2n and f2n + 1 are shifted by (∓ f(0) − f(π/ω))ωτ/π, in the approximation nωτ ≪ 1.
Appendix B: Kepler orbits
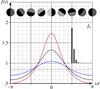 |
Fig. B.1
Phase-light curves for top view on an eccentric planetary orbit. Values for the eccentricity are ϵ = 0 (gray), ϵ = .1 (blue), .2 (black), and .3 (purple, highest peak intensity). The visuals and the inset are for ϵ = .2. |
| Open with DEXTER | |
For planets with noncircular, but eccentric orbits, the distance to the host star is a time-varying periodic function. As a result, the light intensity received by the planet is periodically modulated. We will calculate here the effect of (small) orbital eccentricity on phase light curves. The position vector is no longer given by the circle (1) but with an ellipse with a semimajor axis a along the x-direction and eccentricity ϵ, given by ![]() The Cartesian coordinates (x,y,z) = (x,y,0) are
The Cartesian coordinates (x,y,z) = (x,y,0) are ![]() and the polar coordinates
and the polar coordinates ![]() are given by
are given by 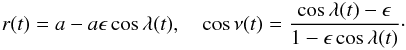 These orbital coordinates are expressed in the eccentric anomaly λ (usually denoted E, see Goldstein 1964). This parameter λ is (implicitly) defined as a function of the orbital phase ωt, from
These orbital coordinates are expressed in the eccentric anomaly λ (usually denoted E, see Goldstein 1964). This parameter λ is (implicitly) defined as a function of the orbital phase ωt, from ![]() An expansion in ϵ for the coordinates in the time variable can be obtained with
An expansion in ϵ for the coordinates in the time variable can be obtained with ![]() In the general case, the eccentricity of the orbit leads to a modulation factor a2/r2(t) in the light curve. The simplest case arises for a homogeneous planet with inclination θ = 0. (Taking MI = 1, ϵ = 0, the half-illuminated disk gives
In the general case, the eccentricity of the orbit leads to a modulation factor a2/r2(t) in the light curve. The simplest case arises for a homogeneous planet with inclination θ = 0. (Taking MI = 1, ϵ = 0, the half-illuminated disk gives ![]() , neglecting the possible 45 degrees glint effect.) The signal is
, neglecting the possible 45 degrees glint effect.) The signal is 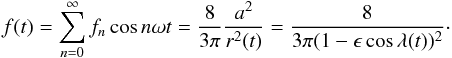 The graph appears in Fig. B.1. Note that Mercury has ϵ = .2.
The graph appears in Fig. B.1. Note that Mercury has ϵ = .2.
We calculate the Fourier coefficients fn by first considering the function 1 /r(t). We use λ as integration variable and require for this substitution ![]() so that
so that 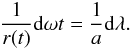 When the complex harmonic einωt is expressed as a periodic function of λ, one obtains the generating function for the Bessel functions (of the first kind)
When the complex harmonic einωt is expressed as a periodic function of λ, one obtains the generating function for the Bessel functions (of the first kind) 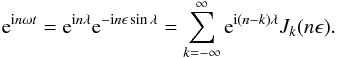 Combining the last two identities and integrating over a full period gives us the Fourier coefficients for 1 /r(t), which are
Combining the last two identities and integrating over a full period gives us the Fourier coefficients for 1 /r(t), which are 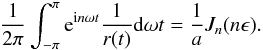 Hence, the reciprocal distance has Fourier series
Hence, the reciprocal distance has Fourier series 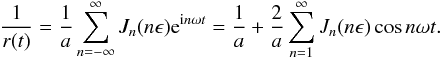 We used J− n(−nϵ) = Jn(nϵ) to get the last identity. It is interesting that the Fourier coefficients of r(t) and of cosθ(t) are Bessel functions, although the functions r(t) and cosθ(t) themselves have no explicit expression in t. The Fourier coefficients of the all powers rN(t), with N ≥ −1 of the radial coordinate r(t) are finite combinations of Bessel functions too.
We used J− n(−nϵ) = Jn(nϵ) to get the last identity. It is interesting that the Fourier coefficients of r(t) and of cosθ(t) are Bessel functions, although the functions r(t) and cosθ(t) themselves have no explicit expression in t. The Fourier coefficients of the all powers rN(t), with N ≥ −1 of the radial coordinate r(t) are finite combinations of Bessel functions too.
The luminosity of a planet is, however, inversely proportional to the square of the distance r(t). We may use the
convolution the series for 1 /r(t) with itself to obtain 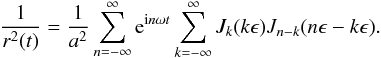 Alternatively we may write
Alternatively we may write 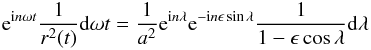 and use the series
and use the series 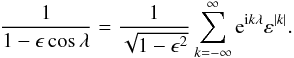 The parameter ε is a new measure of the orbital eccentricity (also in the interval [ 0,1 ]) defined with
The parameter ε is a new measure of the orbital eccentricity (also in the interval [ 0,1 ]) defined with ![]() . We may obtain a second way to express the Fourier series
. We may obtain a second way to express the Fourier series 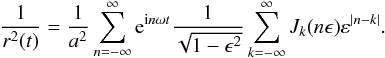 We can now pick out the Fourier coefficients of the light curve. They are, for n ≥ 1,
We can now pick out the Fourier coefficients of the light curve. They are, for n ≥ 1, 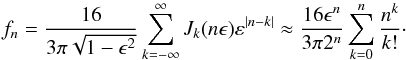 (B.1)The second, approximate equality contains the lowest-order contributions in ϵ. The finite sum is the Taylor polynomial of degree n for the function exp(n). Therefore the coefficients drop to zero exponentially if ϵ< 2/e, as fn ~ ϵnen/ 2n.
(B.1)The second, approximate equality contains the lowest-order contributions in ϵ. The finite sum is the Taylor polynomial of degree n for the function exp(n). Therefore the coefficients drop to zero exponentially if ϵ< 2/e, as fn ~ ϵnen/ 2n.
Since Earth-like planets with a stable water-ice equilibrium will not likely occur for orbits that are too eccentric, we are mainly interested at low values of ϵ. With the above equations it is possible to express the sine components as linear combinations in ϵ of the cosine components for exact circular orbits.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


