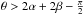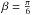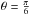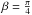| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201424992 | |
| Published online | 19 June 2015 | |
Fourier spectra from exoplanets with polar caps and ocean glint⋆
Delft Institute of Applied Mathematics, Technical University
Delft,
Mekelweg 4,
2628 CD
Delft,
The Netherlands
e-mail:
p.m.visser@tudelft.nl
Received: 15 September 2014
Accepted: 10 February 2015
Context. The weak orbital-phase dependent reflection signal of an exoplanet contains information on the planet surface, such as the distribution of continents and oceans on terrestrial planets. This light curve is usually studied in the time domain, but because the signal from a stationary surface is (quasi)periodic, analysis of the Fourier series may provide an alternative, complementary approach.
Aims. We study Fourier spectra from reflected light curves for geometrically simple configurations. Depending on its atmospheric properties, a rotating planet in the habitable zone could have circular polar ice caps. Tidally locked planets, on the other hand, may have symmetric circular oceans facing the star. These cases are interesting because the high-albedo contrast at the sharp edges of the ice-sheets and the glint from the host star in the ocean may produce recognizable light curves with orbital periodicity, which could also be interpreted in the Fourier domain.
Methods. We derive a simple general expression for the Fourier coefficients of a quasiperiodic light curve in terms of the albedo map of a Lambertian planet surface. Analytic expressions for light curves and their spectra are calculated for idealized situations, and dependence of the spectral peaks on the key parameters inclination, obliquity, and cap size is studied.
Results. The ice-scattering and ocean glint contributions can be separated out, because the coefficients for glint are all positive, whereas ice sheets lead to even-numbered, higher harmonics. An in-view polar cap on a planet without axial tilt only produces a single peak. The special situation of edge-on observation, which is important for planets in transit, leads to the most pronounced spectral behavior. Then the respective spectra from planets with a circumventing ocean, a circular ocean (eyeball world), polar caps, and rings, have characteristic power-law tails n-2, n−7/2, n-4, and (−1)n + 1n-2.
Conclusions. Promising recently discovered planetary systems may be selected as candidates for long-term (multiyear) observation: their Fourier spectra could separate the different planets and reveal or identify a water-covered planet with polar caps.
Key words: planets and satellites: detection / planets and satellites: surfaces / methods: analytical / planets and satellites: oceans / planets and satellites: rings / techniques: photometric
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
In the past decade more than a thousand planets near other stars have been found, proving that nearly every star has planets. The methods of discovery range from direct detection, by watching their birth in the circumstellar planetary disks (Greaves et al. 2005), to more indirect detection in the stellar light dip during the passage of a transiting planet in front of its host star (Hidas et al. 2005; Steffen et al. 2012) and in the time-varying phases from reflected star light (Gaulme et al. 2010). Indirectly inferring the planet’s existence is possible by monitoring the motion of the host star (Benedict et al. 2002) about the common center of mass via measurement of the star’s position coordinates or its Doppler-shifted velocity (Mayor & Queloz 1995), or through the detection of stellar light variations due to the effect of the ellipsoidal deformation of the star by a planet (Welsh et al. 2010).
The phase light curve, which is the (for a twin Earth 10-10 times) weaker overall reflection signal of an orbiting planet on top of the direct stellar light, is a periodic function in time. This periodicity arises as the following combination of different effects: (i) for a noncircular orbit the distance to the star varies, so the planet generally scatters more light at periastron and less at a-periastron (see Appendix). (ii) For inclined observation directions (not top view) the planet exhibits phases, creating waxing and waning sickle shapes similar to the Moon’s phases. A sickle shape gives off less light than the fully illuminated disk. Hence the overall (disk-integrated) intensity shows variations even though these shapes cannot be resolved (Green et al. 2003; Dyudina et al. 2005; Snellen et al. 2009). (iii) For an inhomogeneous planet surface, the net reflection also changes with time because different regions are illuminated at different times as a consequence of rotation or orbital motion (Ford et al. 2001). This phase-dependent light curve can, in fact, reveal part of the surface map (Cowan et al. 2009, 2013). The study of a planet’s surface requires capturing reflected photons, but not spatially resolving the planet.
Planet geometries and viewing configurations.
We advocate making an exceedingly long continuous observation of one exoplanetary system, as suggested by Cowan & Agol (2008), for the purpose of obtaining the Fourier transform of the net intensity. Ideally, the observation should last several orbits and cover a large optical range, without a thermal component. It would be possible to use data from the Kepler satellite (Borucki 2009), or a promising extrasolar system may be found by the future PLATO mission (Catala 2009). The Fourier analysis of this long-duration campaign has clear advantages. The bright glare from the parent star, (i) and (ii) signal from irregular time-varying cloud patterns; and (iii) random noise leave a continuous spectrum and can be filtered out (which is what Fourier transforms are generally used for). On the other hand, stationary surface patterns from land and oceans on the planet give spectral peaks (see the periodogram in Pallé et al. 2008). The diurnal (rotational) and annual (orbital) motion generally result in a mixed time signal, which could be messy; but (iv) the spectrum has nonoverlapping peaks allowing spin-orbit tomography (as proposed by Fujii & Kawahara 2012). Similarly, in a multiplanet system, orbital frequencies are usually incommensurable (not in orbital resonance) such that (v) spectral peaks from different planets can also be separated out. Signals originating from different effects can be distinguished more easily in the spectrum (vi). For example, diffusive (Lambertian) scattering only yields even higher harmonics (see Cowan et al. 2013), which could be used to separate it from other effects such as ocean glint (Williams & Gaidos 2008; Oakley & Cash 2009; Robinson et al. 2010; Zugger et al. 2010). The signal-to-noise ratio in spectral peaks of phase curves is enhanced; (vii) and may become comparable to a transit signal (after multiyear integration).
In this paper, we calculate the Fourier spectra of the light intensity from planets with particularly simple, but interesting geometries that may arise when the planet is covered only in water and ice. The geometry for a spinning planet can be described with two circular symmetric polar ice caps, or, when a planet is tidally locked, with a circular ocean facing the star. These cases are interesting because these planets fall right in the habitable zone, where water and ice coexist. The phase light curve for these geometries is strongest: Fourier peaks are most pronounced for these symmetric cases, and visibility should be optimal. We also exploit the property that liquid water predominantly reflects specularly and is otherwise a strong absorber, whereas snow is nature’s best diffusive reflector. At the same time, a simple symmetric configuration leads to mathematical simplicity, with the possibility of deriving closed analytical expressions for key planetary parameters, such as polar cap extension α and obliquity β.
The structure of this paper is as follows. In Sect. 2 we introduce the general framework of our model; the notation and our model assumptions. The influence of fluctuations from the stellar source and of surface-obscuring planetary clouds on the spectrum is briefly considered. In Sect. 3 we show that the scattering- and glint contributions fI and fL to the light curve are generally quasiperiodic, and then we demonstrate how the coefficients of the periodic spectrum of a banded planet are obtained. We derive exact formulas for these coefficients for the Lambertian phase curve and for the standard Fresnel light curve, corresponding to a snowball planet and an ocean-covered planet. In Sect. 4 we consider planets with polar caps, and derive and study the spectra for interesting special cases. The last two sections deal with the signals from a tidally-locked eyeball planet (Sect. 5) and planets with Saturn-like rings (Sect. 6). These geometries are illustrated in Table 1. In the Appendices, we discuss how a transit affects the spectrum, address the problem of observation gaps, and show how the main results of the paper can be extended for noncircular planet orbits, by adding corrections due to the (small) ellipticity of a Kepler orbit.
2. Fourier series for light curves
The central star is placed at the origin of our coordinate system and the planet, with position r(t), moves in a circular orbit with time t as 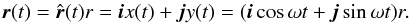 (1)We denote with ω the (angular) orbital frequency: the orbital period is 2π/ω, one planet year. Influences from companion moons and other planets on r(t) are also neglected (orbit eccentricity ϵ ≠ 0 is considered in Appendix B). The polar axis
(1)We denote with ω the (angular) orbital frequency: the orbital period is 2π/ω, one planet year. Influences from companion moons and other planets on r(t) are also neglected (orbit eccentricity ϵ ≠ 0 is considered in Appendix B). The polar axis 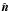 of the planet lies in the xz plane and has obliquity β. The observer at Earth is located (at a distance L) in the direction
of the planet lies in the xz plane and has obliquity β. The observer at Earth is located (at a distance L) in the direction 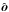 :
: 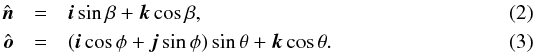 It is natural to choose the obliquity (tilt angle) β and the inclination (polar observation angle) θ in the interval
It is natural to choose the obliquity (tilt angle) β and the inclination (polar observation angle) θ in the interval ![\hbox{$[0,\frac{\pi}{2}]$}](/articles/aa/full_html/2015/07/aa24992-14/aa24992-14-eq22.png) .
.
2.1. Configurations and their symmetry
We assume that the rotation frequency Ω is sufficiently slow that the planet is well approximated with a sphere (for planet oblateness, see Dyudina et al. 2005) and neglect precession on the timescale of observation. Ice sheets and land masses rotate about the axis 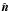 . In particular, polar caps do not grow and shrink significantly with the seasons. There are no effects from oceans waves or foam (Vokroughlicky & Farinella 1995). The atmosphere is at least partially transparent, such that seasonal clouds patterns contribute little, although irregular cloud patterns can lead to interference with the Fourier peaks. We will describe the surface with an (ice-) albedo map and an (ocean-) reflectivity map (MI and ML, respectively). Because the maps rotate about
. In particular, polar caps do not grow and shrink significantly with the seasons. There are no effects from oceans waves or foam (Vokroughlicky & Farinella 1995). The atmosphere is at least partially transparent, such that seasonal clouds patterns contribute little, although irregular cloud patterns can lead to interference with the Fourier peaks. We will describe the surface with an (ice-) albedo map and an (ocean-) reflectivity map (MI and ML, respectively). Because the maps rotate about 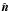 , they have a periodic time dependence with period 2π/ Ω. The annual and diurnal motion may give rise to periodicity in the reflected light signal. Of course, the diurnal period on the planet is 2π/ (Ω − ω).
, they have a periodic time dependence with period 2π/ Ω. The annual and diurnal motion may give rise to periodicity in the reflected light signal. Of course, the diurnal period on the planet is 2π/ (Ω − ω).
We neglected non-Lambertian scattering and polarization effects (Stam et al. 2006; Zugger et al. 2010). Thermal light from the planet is assumed to be absent or filtered out (for the thermal light-signal, see Cowan et al. 2012). The star is also not deformed by the planet (for ellipsoidal variations, see Welsh et al. 2010). We further make the standard approximations that the planet is much smaller than the central star s ≪ S (s and S are the respective radii of planet and star), the star is much smaller than orbital radius S ≪ r, and relative motion of Earth (parallax) is irrelevant r ≪ L. Since s2/ 4r2 is the fraction of star light received by the planet, we normalize the light curve f(t) conveniently with F(t) = f(t)Is2/ 4r2, with I, F denoting the respective observed stellar and planet luminosities.
The reflected light curve for one planet is now in general a quasiperiodic function of time (derived in Sect. 3), consisting of discrete peaks at multiples of the base frequencies ω and Ω: 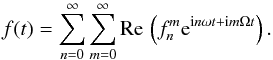 (4)Since f is a linear function of the maps MI and ML, and because the Fourier transform is linear, the Fourier coefficients
(4)Since f is a linear function of the maps MI and ML, and because the Fourier transform is linear, the Fourier coefficients 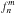 are also linear functions of the planet surface maps. Cowan et al. (2013) calculated the contributions from the spherical harmonics
are also linear functions of the planet surface maps. Cowan et al. (2013) calculated the contributions from the spherical harmonics 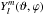 to f(t) (with respect to the rotation axis). Hence, there is also a linear transformation between their coefficients
to f(t) (with respect to the rotation axis). Hence, there is also a linear transformation between their coefficients 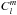 of the surface maps and the Fourier peaks
of the surface maps and the Fourier peaks 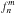 defined here. The spherical wave expansion would be useful in our context; they may almost diagonalize the mapping.
defined here. The spherical wave expansion would be useful in our context; they may almost diagonalize the mapping.
For zero eccentricity, zero inclination, zero obliquity (ϵ = θ = β = 0), a banded planet has no time-varying signal. A nonbanded planet for the same case, however, can have a diurnal signal: then m-peaks appear only for n = 0. If the vectors orbit-normal k, the periastron i (in case of an ellipse), observation direction 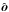 , and polar axis
, and polar axis 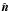 (in case of a inhomogeneous surface) lie in one plane, then the light signal of a banded planet will be an even, periodic function with respect to the inferior conjunction, when the planet is in-between the star and Earth. There are n-peaks occurring only for m = 0 and the fn0 are real numbers,
(in case of a inhomogeneous surface) lie in one plane, then the light signal of a banded planet will be an even, periodic function with respect to the inferior conjunction, when the planet is in-between the star and Earth. There are n-peaks occurring only for m = 0 and the fn0 are real numbers, 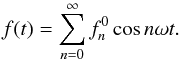 (5)Otherwise, if these vectors break the orbital symmetry so that they are not in one plane, the light signal of a banded planet is not an even function, and contains cosine as well as sine components.
(5)Otherwise, if these vectors break the orbital symmetry so that they are not in one plane, the light signal of a banded planet is not an even function, and contains cosine as well as sine components.
2.2. Effect of stellar variability and cloud cover
Because the reflected light signal involves the product of the source function I(t) with f(t), fluctuations in stellar intensity on orbital timescales disturb the signal. Consider, for example, an ideal light curve consisting of one harmonic at frequency nω. If we let dI(t) represent the stellar noise, with variance Var I, then the measured signal in the time domain is F(t) = (I0 + dI(t))(f0 + fncosnωt)s2/ 4r2. The noise term dI(t)f0 interferes with the wanted signal I0fncosnωt. One requires I0 | fn | ≫ (Var I)1/2f0 to resolve the cosine. The noise for solar fluctuations at 10-8 Hz is due to the 11 yr solar cycle, and has a level of 10-3I0 (Aigrain et al. 2004). For a quiet solar-type star, the scattered light curve can be observed, in principle, for | fn | ≫ 10-3f0. See Lean (2000), for a reconstruction of the past 400 yr solar irradiance. Of course, the photometry must then be sensitive enough to detect the fraction fn/f0 of the average planet luminosity. It is important to overcome the challenge of separating the direct starlight from the planet’s reflection – in the telescope, with a coronagraph or an occulting star shade – especially if one wants to remove large stellar background noise too. If the starlight cannot be shielded, we require s2 | fn | ≫ 10-3r2. This is possible for Jupiter-sized planets near dwarf stars, as was done by Snellen et al. (2009).
An astrophysicist, looking for planets around other stars, can search for peaks in the long duration intensity Fourier spectrum. In practice, the number of observable peaks in (4) will be limited by stellar noise and observation time (and detector sensitivity). We now estimate the noise-requirement for observing the peaks. For a finite observation time T, one may use the standard truncated Fourier spectrum FT(ν) = T−1/2 ∫ F(t)e−iνtdt; the integration of t is over [ 0,T ]. For our periodic light curve (4) this gives ![\begin{eqnarray*} F_T(\nu) = \frac{s^2}{8r^2} \sum_{nm} \left[f^m_n I_T\left(\nu-n\omega-m\Omega\right) \!+\! (f^m_n)^* I_T\left(\nu\!+\!n\omega+m\Omega\right)\right] . \end{eqnarray*}](/articles/aa/full_html/2015/07/aa24992-14/aa24992-14-eq70.png) Hence, every peak becomes convoluted with the (truncated) spectrum IT(ν) of the source I(t). Noise at the frequency ν from the stellar source is quantified by the power spectrum ST(ν) = | IT(ν) | 2. For T − → ∞, this function has a limit for all ν ≠ 0, with the lower frequencies having the slowest convergence. At ν = 0, ST has a peak of width 1 /T and height ST(0) = I02T. Thus, the central peak in IT(ν) has strength I0T1/2. To observe the peak fn at ν = nω in F(ν), it is therefore required that I0T1/2 | fn | ≫ ST(nω)1/2f0 (peak maximum above noise) and that ωT ≫ 1 (peak sufficiently narrow). We can now estimate the noise level at ν = nω, using the property that the integrated power spectrum equals the variance Var I. For a frequency interval of size Δν>ω around the peak at nω, one obtains Var I/ω> Var I/ Δν>ST(nω). Hence, if ωT> 1, the condition for the spectral noise may be more easily fulfilled than the corresponding variance requirement for a time series. We need roughly (ωT)1/2 | fn | ≫ 10-3f0. Hence, nine planet revolutions would enhance the signal with a factor 3 over one round trip.
Hence, every peak becomes convoluted with the (truncated) spectrum IT(ν) of the source I(t). Noise at the frequency ν from the stellar source is quantified by the power spectrum ST(ν) = | IT(ν) | 2. For T − → ∞, this function has a limit for all ν ≠ 0, with the lower frequencies having the slowest convergence. At ν = 0, ST has a peak of width 1 /T and height ST(0) = I02T. Thus, the central peak in IT(ν) has strength I0T1/2. To observe the peak fn at ν = nω in F(ν), it is therefore required that I0T1/2 | fn | ≫ ST(nω)1/2f0 (peak maximum above noise) and that ωT ≫ 1 (peak sufficiently narrow). We can now estimate the noise level at ν = nω, using the property that the integrated power spectrum equals the variance Var I. For a frequency interval of size Δν>ω around the peak at nω, one obtains Var I/ω> Var I/ Δν>ST(nω). Hence, if ωT> 1, the condition for the spectral noise may be more easily fulfilled than the corresponding variance requirement for a time series. We need roughly (ωT)1/2 | fn | ≫ 10-3f0. Hence, nine planet revolutions would enhance the signal with a factor 3 over one round trip.
A similar analysis can be used to estimate the effect of irregular cloud patterns over a planet surface with, for example, (Titan-like) glinting lakes. If clouds obscure the surface 90% of the time and expose surface lakes 10% of the time, the effect is that the underlying periodic glint signal is multiplied with a fluctuating function with average I0 = .1 and variance Var I = .1 − .12 = .09. The peaks appear for (ωT)1/2 | fn | ≫ (Var I)1/2f0/I0 = 3f0. This requires over 60 periods. Of course, the clouds have their own (Lambertian) average contribution to the light curve.
If sharp distinct peaks are resolved in F(ν), the observer may obtain a base spectral structure with harmonics f10, f20, f30 corresponding to the planet’s annual motion. When side structures f11, f21, f31, etc. of similar pattern can be resolved, this could indicate the rotation of a nonbanded planet (the planet has detectable spots). Ideally, the frequencies nω + mΩ have incommensurable base frequencies ω, Ω, because then none of the peaks interfere. The Fourier analysis of the reflection signal from exoplanets will obviously be spoiled if the star variability is strongly periodic. Likewise, surface mapping becomes impossible if the clouds patterns have diurnal periodicity themselves.
3. Scattering and reflecting surfaces
We describe the planet surface with two maps, MI and ML, for the high-albedo (ice, snow) regions and for oceans (liquid). We are interested in high-contrast situations where MI equals one on ice and zero elsewhere (expressions in the next section allow for an albedo factor). The ice scattering is assumed to be Lambertian, isotropically in all directions away from the surface. Ideally, the liquid map ML also equals one or zero and indicates whether there is open ocean or not. (Reduced visibility from cloud cover could be accounted for with a reduction factor.) A planet with an ice and liquid surface would give a phase light curve that is the sum of the two independent contributions 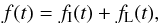 where I is for ice (methane or water) and L is for liquid (methane or water).
where I is for ice (methane or water) and L is for liquid (methane or water).
A light ray from the central star that hits the planet surface has the (unit) direction vector 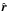 and can be scattered in the direction
and can be scattered in the direction 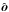 of an observer on Earth. With
of an observer on Earth. With 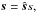 we denote surface vectors (originating from the planet center). Only the surface segment that is the intersection of the illumination
we denote surface vectors (originating from the planet center). Only the surface segment that is the intersection of the illumination 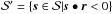 (day-side hemisphere) and the visibility
(day-side hemisphere) and the visibility 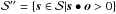 (visible to the observer) contributes to f. The phase light curve, therefore, is a surface integral over the spherical lune
(visible to the observer) contributes to f. The phase light curve, therefore, is a surface integral over the spherical lune 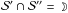 . For a diffusive scattering surface, the light curve contains two inner products, as in
. For a diffusive scattering surface, the light curve contains two inner products, as in 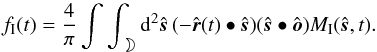 (6)The explicit time-dependence in the albedo map
(6)The explicit time-dependence in the albedo map 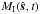 accounts for the rotation. The intensity is properly normalized: using
accounts for the rotation. The intensity is properly normalized: using 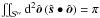 ,
, 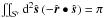 , the overall scattering for a planet with unity albedo M = 1 is precisely
, the overall scattering for a planet with unity albedo M = 1 is precisely 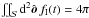 . The surface
. The surface 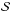 is parametrized with the vector function s(μ,ν) and the surface element in the above integrals needs to be calculated with the Jacobian
is parametrized with the vector function s(μ,ν) and the surface element in the above integrals needs to be calculated with the Jacobian 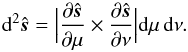 (7)We use
(7)We use 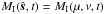 for rotating maps (ice, land, ocean, or otherwise) in non-rotating spherical coordinates (μ,ν); see Table 2 for the parameters used. To find the corresponding coordinates (ϑ,ϕ) on the fixed map MI(ϑ,ϕ) in the rotating frame with respect to the axis
for rotating maps (ice, land, ocean, or otherwise) in non-rotating spherical coordinates (μ,ν); see Table 2 for the parameters used. To find the corresponding coordinates (ϑ,ϕ) on the fixed map MI(ϑ,ϕ) in the rotating frame with respect to the axis 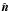 as function of (μ,ν,t), one may use the following relation:
as function of (μ,ν,t), one may use the following relation: 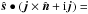

Parameters used in modeling.
3.1. Fourier spectrum from Lambertian surface maps
We are now ready to derive a general expression relating spectral peaks of the signal (6) to a surface albedo map MI. For a unit vector 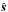 on the unit sphere in cylindrical coordinates (ρ,ν,z), we substitute
on the unit sphere in cylindrical coordinates (ρ,ν,z), we substitute 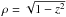 so that the planet surface is parametrized with (ν,z), as
so that the planet surface is parametrized with (ν,z), as  It follows that
It follows that 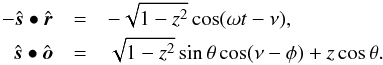 The circle that borders the visible region is found for
The circle that borders the visible region is found for 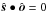 , hence the limb has the coordinate
, hence the limb has the coordinate 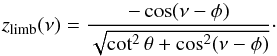 (8)Using the inner products and the surface element
(8)Using the inner products and the surface element 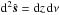 , the double integral in (6) is expressed as the following repeated integral:
, the double integral in (6) is expressed as the following repeated integral: 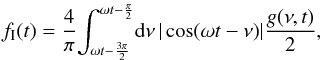 where the pattern function g(ν,t) contains the z integration over the interval between the limb point (8) and the point with z = 1, i.e.,
where the pattern function g(ν,t) contains the z integration over the interval between the limb point (8) and the point with z = 1, i.e., 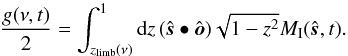 (9)Since the rotation axis
(9)Since the rotation axis  and the observation direction
and the observation direction  are constant, g(ν,t) characterizes the scattering pattern from the visible regions. When ν and t are considered independent variables, then
are constant, g(ν,t) characterizes the scattering pattern from the visible regions. When ν and t are considered independent variables, then 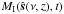 is periodic in ν (because
is periodic in ν (because 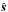 is periodic in ν) and in Ωt (modulo 2π) and therefore
is periodic in ν) and in Ωt (modulo 2π) and therefore 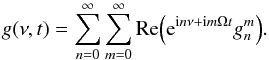 (10)When we make the substitution
(10)When we make the substitution 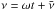
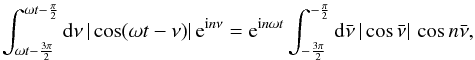 and use this relation in the remaining integral to get
and use this relation in the remaining integral to get 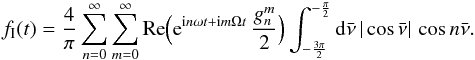 We find that the Fourier coefficients of fI are each related to the corresponding Fourier coefficients of g by
We find that the Fourier coefficients of fI are each related to the corresponding Fourier coefficients of g by 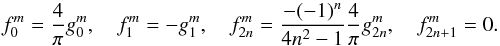 (11)The expressions (11) are key results of this paper. The Fourier coefficients
(11)The expressions (11) are key results of this paper. The Fourier coefficients 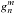 of the pattern function g(ν,t) found from the surface map
of the pattern function g(ν,t) found from the surface map 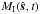 immediately gives us the spectrum of the quasiperiodic light curve of a planet.
immediately gives us the spectrum of the quasiperiodic light curve of a planet.
There are several reasons why the linear transformation from MI to 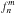 is not invertible. Firstly, the region with polar angles
is not invertible. Firstly, the region with polar angles 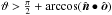 below the southern circle (i.e.,
below the southern circle (i.e., 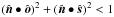 ) is permanently inaccessible to the observer. Thus any map that is zero outside and arbitrary inside this circle gives no signal. (These maps are in the null space of the transformation, see Cowan et al. 2013) Secondly, consider the case that MI is only a function of z, not of ν and t. This is the case for a banded planet with zero obliquity (see Sect. 4.3). If a banded map is also zero below the northern circle z = sinθ, it can be seen that the integral in expression (9) for g(ν) effectively runs over z-values from sinθ to 1. The dependence on ν comes from the factor
) is permanently inaccessible to the observer. Thus any map that is zero outside and arbitrary inside this circle gives no signal. (These maps are in the null space of the transformation, see Cowan et al. 2013) Secondly, consider the case that MI is only a function of z, not of ν and t. This is the case for a banded planet with zero obliquity (see Sect. 4.3). If a banded map is also zero below the northern circle z = sinθ, it can be seen that the integral in expression (9) for g(ν) effectively runs over z-values from sinθ to 1. The dependence on ν comes from the factor 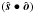 only, which yields a single cosine. Therefore, the spectrum has just two peaks, with amplitudes f00 and f10, and most of the information from the banded structure is lost. Thirdly, if a banded planet with zero obliquity is also observed edge-on, the inclination is
only, which yields a single cosine. Therefore, the spectrum has just two peaks, with amplitudes f00 and f10, and most of the information from the banded structure is lost. Thirdly, if a banded planet with zero obliquity is also observed edge-on, the inclination is 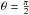 and zlimb = ±1. Then the z integral vanishes for + 1 and gives the same overall albedo constant for − 1. This implies that the light curve is indistinguishable from that of a homogeneous planet. Finally, if the rotation period and orbital period are commensurable, which is when Ω /ω is a rational number, then different combinations of the coefficients
and zlimb = ±1. Then the z integral vanishes for + 1 and gives the same overall albedo constant for − 1. This implies that the light curve is indistinguishable from that of a homogeneous planet. Finally, if the rotation period and orbital period are commensurable, which is when Ω /ω is a rational number, then different combinations of the coefficients  have the same harmonic frequency and thus interfere. This is the case in particular if the ratio is not very large (or very small). Different maps can give the same signal, and detailed structure is lost.
have the same harmonic frequency and thus interfere. This is the case in particular if the ratio is not very large (or very small). Different maps can give the same signal, and detailed structure is lost.
3.2. Fourier coefficients for a banded planet
The surface pattern of a rotating planet is stationary only if the pattern is banded; that is, if the rotation axis is also an axis of symmetry for the pattern. In other words, the planet has no spots (like Jupiter or Neptune). The function  is invariant under rotation about
is invariant under rotation about 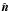 and constant in time; then the planet’s rotation is unobservable. It follows from (9), (10) that
and constant in time; then the planet’s rotation is unobservable. It follows from (9), (10) that  for all m except m = 0. In what follows, we only consider banded planets (and tidally locked planets, with Ω = ω), and, therefore, drop the index m from all following expressions.
for all m except m = 0. In what follows, we only consider banded planets (and tidally locked planets, with Ω = ω), and, therefore, drop the index m from all following expressions.
If we assume the further (reflection) symmetry  , we can simplify the expression for the coefficients gn. Let us consider first g1. We make use of the fact that e−iν is opposite for values of ν that are π apart. Points with z> 0, which are invisible, are opposite to points with z< 0, which are visible. This allows the z integral (9) for g(ν) to be split into a sum of integrals for two hemispheres, and to condense into one ρ integral over the north hemisphere. Using ρdz = −(ρ2/z)dρ, we may write
, we can simplify the expression for the coefficients gn. Let us consider first g1. We make use of the fact that e−iν is opposite for values of ν that are π apart. Points with z> 0, which are invisible, are opposite to points with z< 0, which are visible. This allows the z integral (9) for g(ν) to be split into a sum of integrals for two hemispheres, and to condense into one ρ integral over the north hemisphere. Using ρdz = −(ρ2/z)dρ, we may write 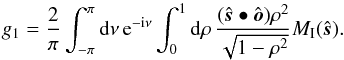 (12)For even coefficients, the phase-factor e−2inν for opposite points is the same, hence
(12)For even coefficients, the phase-factor e−2inν for opposite points is the same, hence  (13)The dependence on limb position in (9) has been removed in (12), (13). Note the distinct absolute-value of the inner product in (13) is absent in (12). The assumption of reflection symmetry must be independently validated before these expressions may be used.
(13)The dependence on limb position in (9) has been removed in (12), (13). Note the distinct absolute-value of the inner product in (13) is absent in (12). The assumption of reflection symmetry must be independently validated before these expressions may be used.
3.3. Fourier coefficients for a homogenous planet
Consider the case of a planet with a homogeneous scattering surface. The orientation of the rotation axis is irrelevant and the symmetry about the z axis is only broken by the fact that the observer is viewing from an inclined direction, and we may set φ = 0 in (3). We calculate the light curve f(t) and its Fourier coefficients fn. It turns out that, on the one hand, the time-signal f(t) is most conveniently evaluated using a new coordinate system that exploits the symmetry about  , but that the peak intensities fn, on the other hand, are most directly derived from the function g(ν). We thus write the surface vector s in spherical coordinates (s,μ,ν) with respect to an orthogonal basis fixed by o and r as
, but that the peak intensities fn, on the other hand, are most directly derived from the function g(ν). We thus write the surface vector s in spherical coordinates (s,μ,ν) with respect to an orthogonal basis fixed by o and r as  We require for (6) the inner products
We require for (6) the inner products  and the surface element (7) is
and the surface element (7) is 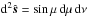 . Let ϕ be the scattering angle, between r and o, so that
. Let ϕ be the scattering angle, between r and o, so that 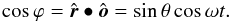 The condition
The condition 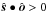 implies that μ lies in the interval [ 0,π ] and
implies that μ lies in the interval [ 0,π ] and 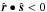 implies that ν lies in the interval [ 0,ϕ ]. With these definitions, and by setting MI = 1, formula (6) reduces to a well-known form (van Hulst 1980)
implies that ν lies in the interval [ 0,ϕ ]. With these definitions, and by setting MI = 1, formula (6) reduces to a well-known form (van Hulst 1980) 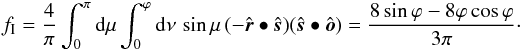 Completely expanded, this yields
Completely expanded, this yields 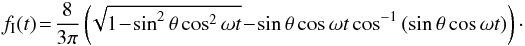 Note that, for top view θ = 0, the signal is constant. As previously indicated, for the Fourier components, we substitute MI = 1, φ = 0 and (8) in the pattern function (9) and obtain
Note that, for top view θ = 0, the signal is constant. As previously indicated, for the Fourier components, we substitute MI = 1, φ = 0 and (8) in the pattern function (9) and obtain 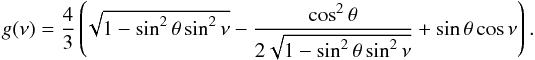 There are two steps to obtain the Fourier coefficient from this function. First, calculate the Taylor series in the powers x2k = sin2kθ, and, then, expand
There are two steps to obtain the Fourier coefficient from this function. First, calculate the Taylor series in the powers x2k = sin2kθ, and, then, expand 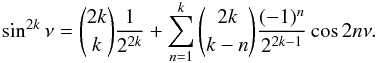 Collecting the coefficients in front of the cosines leads to the result
Collecting the coefficients in front of the cosines leads to the result 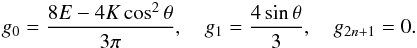 The functions K = K(sinθ) and E = E(sinθ) are the complete elliptic integrals of the first and second kind; the inclination θ has the role of the so-called modular angle. The higher-order coefficients lead to the hypergeometric function
The functions K = K(sinθ) and E = E(sinθ) are the complete elliptic integrals of the first and second kind; the inclination θ has the role of the so-called modular angle. The higher-order coefficients lead to the hypergeometric function 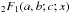 :
: 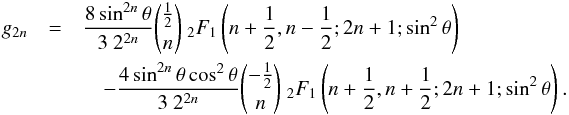 The hypergeometric functions in g2n can be expanded into K and E. With (11), the peak values fn follow. We obtain for the first four coefficients
The hypergeometric functions in g2n can be expanded into K and E. With (11), the peak values fn follow. We obtain for the first four coefficients 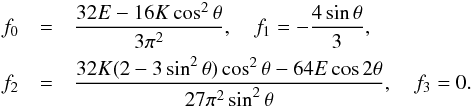 (14)If one observes the orbital plane edge on, then
(14)If one observes the orbital plane edge on, then 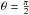 and ϕ(t) = | ωt | for − π ≤ ωt ≤ π. The standard Lambertian phase curve for in-plane observation of a planet or moon is
and ϕ(t) = | ωt | for − π ≤ ωt ≤ π. The standard Lambertian phase curve for in-plane observation of a planet or moon is 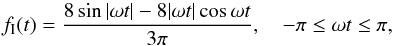 (15)with Fourier coefficients,
(15)with Fourier coefficients, 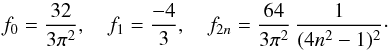 (16)The graph is plotted in Fig. 1. The coefficients (14), (16) drop to zero with the fourth power in n, such that f4 is already much smaller than | f1 |. Figure 2 shows the ratios of coefficients gn as function of observation angle θ. If the planet radius s and albedo were determined with other methods, then the first coefficient f1 could be used to estimate or verify obliquity. Otherwise, the relative values of the peaks in the spectrum must be used to obtain orbital parameters. For example, the ratio of the first two peaks f2/f1 = −4g2/ 3πg1 could be used to find θ. For this purpose, in Fig. 2 we plotted the ratios as a function of θ. The overall complex phase φ of the peaks, which was set to zero for the sake of convenience in our calculations, is just the orbital phase with respect to the inferior conjunction (in-between Earth and the star). The absence of f3, f5 would indicate that the planet is a diffusive scatterer without specular glint. The condition | fn | ≫ 10-3f0, derived in Sect. 2.2, valid for a Sun-type star observed for one year, implies that f8 is swamped in the stellar noise.
(16)The graph is plotted in Fig. 1. The coefficients (14), (16) drop to zero with the fourth power in n, such that f4 is already much smaller than | f1 |. Figure 2 shows the ratios of coefficients gn as function of observation angle θ. If the planet radius s and albedo were determined with other methods, then the first coefficient f1 could be used to estimate or verify obliquity. Otherwise, the relative values of the peaks in the spectrum must be used to obtain orbital parameters. For example, the ratio of the first two peaks f2/f1 = −4g2/ 3πg1 could be used to find θ. For this purpose, in Fig. 2 we plotted the ratios as a function of θ. The overall complex phase φ of the peaks, which was set to zero for the sake of convenience in our calculations, is just the orbital phase with respect to the inferior conjunction (in-between Earth and the star). The absence of f3, f5 would indicate that the planet is a diffusive scatterer without specular glint. The condition | fn | ≫ 10-3f0, derived in Sect. 2.2, valid for a Sun-type star observed for one year, implies that f8 is swamped in the stellar noise.
 |
Fig. 1 Standard light curve (15) for a homogeneous (Lambertian) planet: normalized intensity f versus orbital phase ωt, for edge-on observation. The inset shows, to scale, the coefficients gn which are proportional to fn (16) according to (11). |
 |
Fig. 2 Harmonic ratios g2/g1 (blue), g4/g1 (purple) and g6/g1 (orange) for a snowball planet, versus inclination angle θ. These curves can be used to determine the inclination θ or to conclude that the planet is, instead, inhomogeneous. |
3.4. Glint spot on a specular reflecting surface
Consider a reflecting sphere with radius s, placed at the origin, which is illuminated by a point source on the z axis at z = + ∞. Imagine a long cylinder of parallel light rays around the z axis with radius ρ<s and cross-section A = πρ2. The rays inside this cylinder hit the north pole of our sphere from angle zero up to angle θ. Since s is the radius of the sphere, this implies ρ = ssinθ. At the border, the angle of incidence is also θ, so the cylindrical beam is reflected into a segment of the hemisphere with limiting angle 2θ. The total solid angle of the reflected light is therefore given by the integral 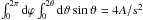 . Because this solid angle is proportional to A, a perfectly reflecting sphere scatters light isotropically in all directions. Since a finite source (at large distance) may be composed of many point sources, a reflecting sphere also scatters the light of a finite source isotropically. The reflection of a metallic planet would, like a garden ball, be equally bright from all directions, and there would be no variation in intensity during its yearly orbit.
. Because this solid angle is proportional to A, a perfectly reflecting sphere scatters light isotropically in all directions. Since a finite source (at large distance) may be composed of many point sources, a reflecting sphere also scatters the light of a finite source isotropically. The reflection of a metallic planet would, like a garden ball, be equally bright from all directions, and there would be no variation in intensity during its yearly orbit.
If the light source is a star with radius S and our sphere is a planet with radius s, the light rays that are incident on the smaller planet are confined to the cone 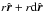 . Here
. Here 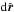 is orthogonal to
is orthogonal to 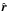 and its length is
and its length is 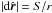 . Since the distance to the observer is very large, the reflected cone is practically collapsed into a line with direction
. Since the distance to the observer is very large, the reflected cone is practically collapsed into a line with direction 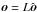 . The points where the light rays are reflected on the surface, form a small ellipse around the central point of reflection
. The points where the light rays are reflected on the surface, form a small ellipse around the central point of reflection 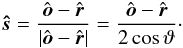 Here ϑ is the angle of incidence with respect to the surface normal, with
Here ϑ is the angle of incidence with respect to the surface normal, with 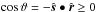 . This ellipse is now given by
. This ellipse is now given by 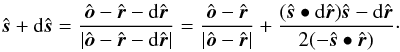 The vector
The vector 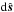 points from the center to the edge of the ellipse and is orthogonal to
points from the center to the edge of the ellipse and is orthogonal to 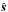 . The ellipse has semiaxes of S/ 2r and S/ 2rcosϑ and an area of
. The ellipse has semiaxes of S/ 2r and S/ 2rcosϑ and an area of  . Ocean waves, however, increase the size of this glint spot. As discussed by Williams & Gaidos (2008), the reflection signal does not significantly change as long as the ocean is wider than the spot. In the limit S/r − → 0, the image of the star becomes a point (except for
. Ocean waves, however, increase the size of this glint spot. As discussed by Williams & Gaidos (2008), the reflection signal does not significantly change as long as the ocean is wider than the spot. In the limit S/r − → 0, the image of the star becomes a point (except for 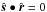 , which is the case of grazing reflection). The conclusion is that, in the regime S ≪ r ≪ L, the reflection signal equals the surface reflectivity at the point of reflection and thus probes the surface along a curve in the band with polar values
, which is the case of grazing reflection). The conclusion is that, in the regime S ≪ r ≪ L, the reflection signal equals the surface reflectivity at the point of reflection and thus probes the surface along a curve in the band with polar values 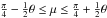 . Close to edge-on observation
. Close to edge-on observation 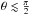 , the entire northern hemisphere is probed because, near inferior conjunction, the glint spot quickly moves from the
, the entire northern hemisphere is probed because, near inferior conjunction, the glint spot quickly moves from the 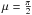 to μ = 0. If we call ℛ(ϑ) the ocean reflectivity for incidence angle ϑ, the signal is
to μ = 0. If we call ℛ(ϑ) the ocean reflectivity for incidence angle ϑ, the signal is 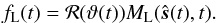 Here and
Here and  is now the (rotating) ocean map. When taking a fixed vector
is now the (rotating) ocean map. When taking a fixed vector 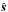 on the surface, this map has the Fourier series
on the surface, this map has the Fourier series 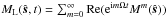 . The glint point (in the nonrotating system) varies periodically over one year as
. The glint point (in the nonrotating system) varies periodically over one year as 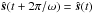 . When we take this periodicity into account, the coefficients for the rotation map are
. When we take this periodicity into account, the coefficients for the rotation map are 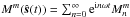 , so that the net function
, so that the net function 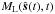 is a quasiperiodic function of t. The reflectivity ℛ is a function of time via ϑ(t), and also varies also annually. Therefore, the light curve for ocean glint, is a product of a periodic with a quasiperiodic function, which is quasiperiodic and has the form (4), just like the light curve for a Lambertian map.
is a quasiperiodic function of t. The reflectivity ℛ is a function of time via ϑ(t), and also varies also annually. Therefore, the light curve for ocean glint, is a product of a periodic with a quasiperiodic function, which is quasiperiodic and has the form (4), just like the light curve for a Lambertian map.
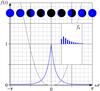 |
Fig. 3 Standard Fresnel light curve (18) from ocean glint for edge-on view (in blue; the Lambertian scattering signal is shown for comparison in gray). The inset shows the spectrum. In the visuals, the glint is yellow. |
3.5. Fourier coefficients for ocean glint
In this section, we derive a compact expression for the ocean glint, the ideal Fresnel curve, and calculate its Fourier peaks. The reflection by a surface of water depends on the angle of incidence ϑ. The reflection coefficients for s-polarized light and p-polarized light are given by the Fresnel equations (Hecht 2002) ![\begin{eqnarray*} {\cal R}_\mathrm{s}(\vartheta) &=& \left(\frac{\sqrt{n^2-\sin^2\vartheta}-\cos\vartheta}{\sqrt{n^2-\sin^2\vartheta}+\cos\vartheta}\right)^2 , \\[0.5mm] {\cal R}_\mathrm{p}(\vartheta) &=& \left(\frac{n^2\cos\vartheta-\sqrt{n^2-\sin^2\vartheta}}{n^2\cos\vartheta+\sqrt{n^2-\sin^2\vartheta}}\right)^2 \cdot \end{eqnarray*}](/articles/aa/full_html/2015/07/aa24992-14/aa24992-14-eq282.png) Taking n = 4/3 for the index of reflection for water (or liquid methane), and assuming that the stellar light is unpolarized (the relative s- and p-intensities are
Taking n = 4/3 for the index of reflection for water (or liquid methane), and assuming that the stellar light is unpolarized (the relative s- and p-intensities are  and
and  ) the net signal from a smooth water surface is
) the net signal from a smooth water surface is 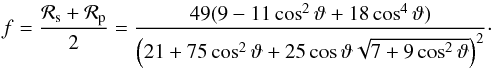 (17)For a planet in orbit, with position vector (1), observed from direction (3), the cosine of the incidence angle varies with time as
(17)For a planet in orbit, with position vector (1), observed from direction (3), the cosine of the incidence angle varies with time as 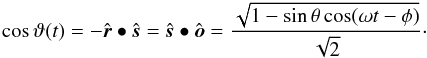 This must be substituted in (17) to get the light curve for a water world (with ocean map
This must be substituted in (17) to get the light curve for a water world (with ocean map 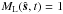 ). The signal is significant if the observer is in the plane of the orbit, for
). The signal is significant if the observer is in the plane of the orbit, for 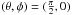 , and
, and  . For this case, we obtain the standard Fresnel light curve, which is
. For this case, we obtain the standard Fresnel light curve, which is 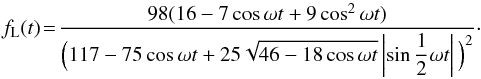 (18)The glint spikes at t = 0, for grazing light rays, when r and o are in the same direction; see Figs. 3 and 4. The width extends to about a quarter of a year. The numerical values of the Fourier peaks are
(18)The glint spikes at t = 0, for grazing light rays, when r and o are in the same direction; see Figs. 3 and 4. The width extends to about a quarter of a year. The numerical values of the Fourier peaks are ![\begin{eqnarray} f_0 &=& 0.12032 , \label{fwater} \\[0.5mm] f_1 &=& 0.181 , \quad f_2 = 0.141 , \quad f_3 = 0.102 , \nonumber \\[0.5mm] f_4 &=& 0.075 , \quad f_5 = 0.055 , \quad f_6 = 0.042 , \quad \mathrm{and} \nonumber \\[0.5mm] f_n &&\approx 50 \Big/ 3\sqrt{7}\pi n^2 \quad \mathrm{if}\quad n \longrightarrow \infty \cdot \nonumber \end{eqnarray}](/articles/aa/full_html/2015/07/aa24992-14/aa24992-14-eq292.png) (19)Observation of these values would strongly indicate that the planet is covered with oceans, composed of water or methane. The coefficients are positive and decay with an inverse square as fn ~ n-2, which is characteristic for functions that are differentiable except at one point (in this case at t = 0). Many peaks can come out of the noise, in theory, for | fn | ≫ 10-3f0. However, the actual sharpness of the t = 0 peak, will limit the validity of our calculated numerical values of fn.
(19)Observation of these values would strongly indicate that the planet is covered with oceans, composed of water or methane. The coefficients are positive and decay with an inverse square as fn ~ n-2, which is characteristic for functions that are differentiable except at one point (in this case at t = 0). Many peaks can come out of the noise, in theory, for | fn | ≫ 10-3f0. However, the actual sharpness of the t = 0 peak, will limit the validity of our calculated numerical values of fn.
3.6. Slushball Earth
An interesting situation occurs for a planet that has an ocean circumventing the equator, and is covered with ice everywhere else. For Earth, this is called slushball Earth (Hoffman et al. 1998; Fairchild & Kennedy 2007; Macdonald et al. 2010); it is the hypotheses that during the periods of global iceage, almost all of the oceans were covered with ice sheets, except for a narrow band at the equator. For an edge-on view, the signal has a maximal intensity: there is the scattering ice with nearly unit albedo and there is a maximal glint effect. The planet can at the same time be found in a transiting orbit, i.e. eclipsing the host star. The light curve is found with the summation of (15), (18), (A.1). A Fourier coefficient is the sum of the expressions (16), (19), (A.2) that follow.
4. Polar caps
We describe the situation with polar caps as  (20)using the Heaviside step function H, assuming that the caps are constant in size. Seasonal growth and decay of the caps are assumed to be small, which is reasonable for larger planets or small obliquity. Hence, MI = 0 for
(20)using the Heaviside step function H, assuming that the caps are constant in size. Seasonal growth and decay of the caps are assumed to be small, which is reasonable for larger planets or small obliquity. Hence, MI = 0 for 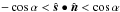 , and unity otherwise. (An albedo factor and a cloud reduction factor could be included.) The border of the north polar icecap is found where
, and unity otherwise. (An albedo factor and a cloud reduction factor could be included.) The border of the north polar icecap is found where 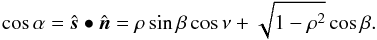 (21)We assume β ≤ α, so that point sk lies on the north polar cap and we assume
(21)We assume β ≤ α, so that point sk lies on the north polar cap and we assume 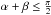 , so that the tropical latitudes are ice free. The radial coordinate ρ for the polar cap edge cap, as a function of ν, denoted ρn, is then the positive solution of the quadratic Eq. (21). One may write this equation and this solution as
, so that the tropical latitudes are ice free. The radial coordinate ρ for the polar cap edge cap, as a function of ν, denoted ρn, is then the positive solution of the quadratic Eq. (21). One may write this equation and this solution as 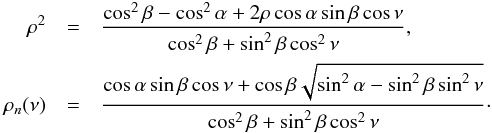 (22)The border of the south-polar cap is found at ρs(ν) = ρn(ν + π).
(22)The border of the south-polar cap is found at ρs(ν) = ρn(ν + π).
 |
Fig. 4 Harmonic ratios f5/f3 (blue), f7/f3 (purple), and f9/f3 (orange) for a planet with permanent ocean glint. The glint spot of a water world with polar caps is continuously visible for |
4.1. Case I: edge-on view
Consider the case that the orbital plane is observed edge on, when 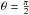 . This important situation arises for extrasolar planets that were discovered with the transit method. During an eclipse, the planet passes between its parent star and Earth, so we observe the orbital plane edge on. The limb is no longer given by (8), but we find that
. This important situation arises for extrasolar planets that were discovered with the transit method. During an eclipse, the planet passes between its parent star and Earth, so we observe the orbital plane edge on. The limb is no longer given by (8), but we find that 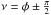 . Between these values, for
. Between these values, for 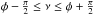 , the pattern function is
, the pattern function is 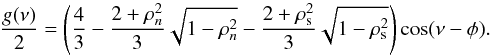 (23)Substitution of (20) in (12), (13) yields the Fourier coefficients
(23)Substitution of (20) in (12), (13) yields the Fourier coefficients 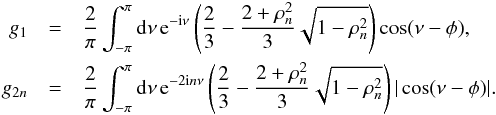 Here we need to substitute the cap-edge function (22). For small β, the coefficients are
Here we need to substitute the cap-edge function (22). For small β, the coefficients are 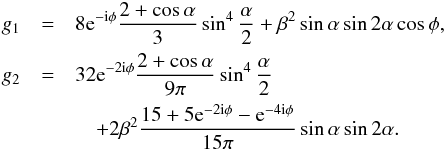 If transits occur, the large signal (A.2) from the stellar light dip has to be carefully subtracted first. Figures 5 and 6 show light curves for an edge-on view in the respective cases of φ = 0 and
If transits occur, the large signal (A.2) from the stellar light dip has to be carefully subtracted first. Figures 5 and 6 show light curves for an edge-on view in the respective cases of φ = 0 and 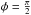 .
.
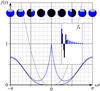 |
Fig. 5 Light curve of planet with polar caps for edge-on observation, |
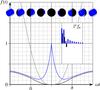 |
Fig. 6 Light curve of planet with polar caps for edge-on observation, |
4.2. Case II: one polar cap in full view
When the limb does not cross the icecaps, one cap is always completely visible and the other cap is entirely obscured. This allows us to go from z to ρ in Eq. (9) and obtain, with substitution, (20) that  (24)For small β the first coefficients become
(24)For small β the first coefficients become 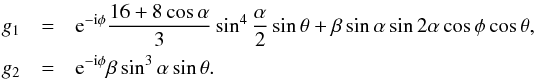
4.3. Case III: zero obliquity
If the rotation axis is vertical, the case β = 0, the symmetry about the z axis is only broken in the observation direction (3). Consider the case that the planet is observed from a direction that has full view onto the polar icecap. Then ρn = ρs = sinα, and (9), (24), with φ = 0, become  There are only two nonzero Fourier coefficients: g0 and g1. The relevant nonzero Fourier coefficient in the signal, f1 = −g1 is reduced from − 4/3 by the factor
There are only two nonzero Fourier coefficients: g0 and g1. The relevant nonzero Fourier coefficient in the signal, f1 = −g1 is reduced from − 4/3 by the factor 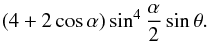 Figure 7 shows an example of this case. A short calculation shows that the glint spot is on an open ocean for
Figure 7 shows an example of this case. A short calculation shows that the glint spot is on an open ocean for 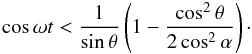 The case of zero obliquity with the observer inside the orbital plane gives the standard Lambertian curve (15) with harmonics (16), as in Fig. 1, except that Eqs. (15), (16) must be multiplied with the cap size dependent reduction factor
The case of zero obliquity with the observer inside the orbital plane gives the standard Lambertian curve (15) with harmonics (16), as in Fig. 1, except that Eqs. (15), (16) must be multiplied with the cap size dependent reduction factor 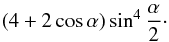 Of course, for an edge-on observation of a water world with a polar cap, the ocean glint is maximal. This effect turns up in the odd harmonic amplitudes, f2n + 1, of the spectrum. When the reflection signal is subtracted from the spectrum, the Lambertian contribution remains, and the extension angle α of the polar caps can be determined from that contribution.
Of course, for an edge-on observation of a water world with a polar cap, the ocean glint is maximal. This effect turns up in the odd harmonic amplitudes, f2n + 1, of the spectrum. When the reflection signal is subtracted from the spectrum, the Lambertian contribution remains, and the extension angle α of the polar caps can be determined from that contribution.
 |
Fig. 7 Light curve for planet with polar caps for inclined observation |
4.4. Case IV: face-on view
We consider, as a last concrete example, the situation that the observer has a top view onto the orbital plane, with the entire northern polar cap also in view. For this case, θ = 0, and we require that 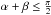 . The pattern function (24) for this situation in terms of the cap edge (22) is
. The pattern function (24) for this situation in terms of the cap edge (22) is 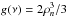 . To find the light curve itself, the Cartesian coordinates (x,y) are most convenient as parameters for the northern hemisphere, where
. To find the light curve itself, the Cartesian coordinates (x,y) are most convenient as parameters for the northern hemisphere, where 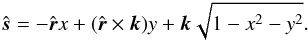 The x and y coordinates are now the corotating coordinates, so that the day-night terminator circle found for
The x and y coordinates are now the corotating coordinates, so that the day-night terminator circle found for 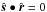 is at x = 0. The surface element (7) is
is at x = 0. The surface element (7) is 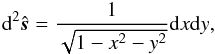 and the inner products are
and the inner products are 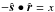 ,
, 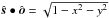 , which implies that
, which implies that 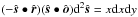 . The border of the polar cap is located at
. The border of the polar cap is located at 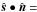
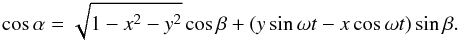 The quadratic form for the projection of the ellipse onto the xy plane is
The quadratic form for the projection of the ellipse onto the xy plane is 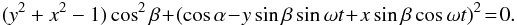 If we solve y as a function of x, we find solutions y+(x) and y−(x). The extreme values for x, where these two solutions connect, are
If we solve y as a function of x, we find solutions y+(x) and y−(x). The extreme values for x, where these two solutions connect, are 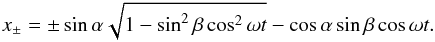 The surface integral in (6) can now be calculated using
The surface integral in (6) can now be calculated using 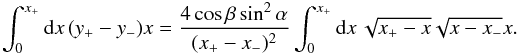 The light curve is therefore given by
The light curve is therefore given by 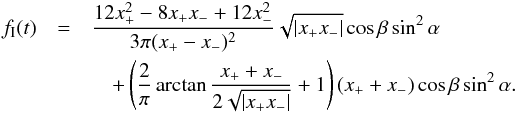 (25)The graph is plotted in Fig. 8 for polar caps that extend 45 degrees and for obliquity of 30 degrees.
(25)The graph is plotted in Fig. 8 for polar caps that extend 45 degrees and for obliquity of 30 degrees.
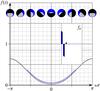 |
Fig. 8 Polar-cap light curve (25) for top view; inclination θ = 0. Cap extension is |
5. Tidally locked planet
When a planet is tidally locked, the same side faces the host star at all times. The substellar point  is constantly directed toward the star and the point
is constantly directed toward the star and the point  on the other side is always in the dark. Apart from moving cloud contributions, the surface pattern will be stationary in the corotating frame. A reflection signal from the planet is time dependent because an observer sees a rotating surface pattern with a constant illumination, instead of a time-varying illumination, as before. Since this is the special case Ω = ω, the general equations of Sect. 3 are valid, but now all coefficients
on the other side is always in the dark. Apart from moving cloud contributions, the surface pattern will be stationary in the corotating frame. A reflection signal from the planet is time dependent because an observer sees a rotating surface pattern with a constant illumination, instead of a time-varying illumination, as before. Since this is the special case Ω = ω, the general equations of Sect. 3 are valid, but now all coefficients 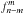 contribute to the same nω-peak in (4), for all m. We proceed, however, by defining a new pattern function. For this situation, we introduce rotating coordinates (ν,z) defined with
contribute to the same nω-peak in (4), for all m. We proceed, however, by defining a new pattern function. For this situation, we introduce rotating coordinates (ν,z) defined with 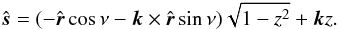 In this coordinate frame, the surface maps MI and ML are only functions of (ν,z), and they are not functions of time. The planet will now have a rotationally symmetric map with respect to the time-varying
In this coordinate frame, the surface maps MI and ML are only functions of (ν,z), and they are not functions of time. The planet will now have a rotationally symmetric map with respect to the time-varying 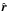 axis, but not with respect to any fixed axis. One expects that for θ ≠ 0 and
axis, but not with respect to any fixed axis. One expects that for θ ≠ 0 and 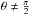 , higher-order odd harmonics from both MI and ML are present in the spectrum. For edge-on observation
, higher-order odd harmonics from both MI and ML are present in the spectrum. For edge-on observation 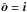 , however, a similar symmetry as for a banded planet with a fixed rotation axis arises. We now have
, however, a similar symmetry as for a banded planet with a fixed rotation axis arises. We now have 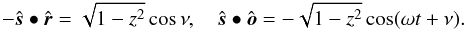 Equation (6) may therefore be expressed in terms of a pattern function g for a locked planet, according to
Equation (6) may therefore be expressed in terms of a pattern function g for a locked planet, according to  and g(ν) is zero for the dark side of the planet,
and g(ν) is zero for the dark side of the planet, 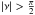 . If we take the same definition (10), then the relation (11) for m = 0, between the harmonics in the signal function f and the pattern function g is valid.
. If we take the same definition (10), then the relation (11) for m = 0, between the harmonics in the signal function f and the pattern function g is valid.
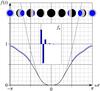 |
Fig. 9 Light curve (26), (27) for an eyeball planet with circular ocean extending over α = π/ 4, with and without glint (blue and black), as given in Eq. (18). The view is edge-on. The snowball light curve (gray) is for comparison. |
5.1. Eyeball worlds
Consider now a tidally locked planet with open water. At the star-facing side, a circular ocean exists with an extension angle α (Pierrehumbert 2011). The rest of the planet is covered in ice, as depicted in the visuals of Fig. 9. Because of oceanic heat transport, according to Hu & Yang (2014), the ocean shape may deviate from a circle for the relevant case of a locked planet near an M-type star. In our model, the edge is now located for 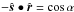 . We therefore assume the following form:
. We therefore assume the following form: 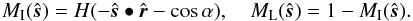 We equate g and f. We have for
We equate g and f. We have for  that g(ν) = (8/3)cosν and for | ν | <α that g(ν) =
that g(ν) = (8/3)cosν and for | ν | <α that g(ν) =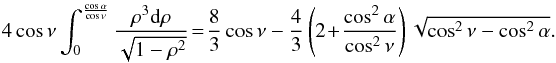 At ν = ±α the pattern function has an infinite respective left- or right-derivative, leading to gn ~ n−3/2.
At ν = ±α the pattern function has an infinite respective left- or right-derivative, leading to gn ~ n−3/2.
 |
Fig. 10 Peak ratios f1/f0 (black), f2/f0 (blue), f3/f0 (purple), and f4/f0 (orange) for an eyeball planet viewed edge-on plotted as a function of the ocean extension angle α. Ocean glint is neglected. |
For 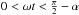 the ocean is not visible, and f equals the snowball signal (15). For
the ocean is not visible, and f equals the snowball signal (15). For 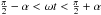 the ocean is partly visible, and the phase curve is
the ocean is partly visible, and the phase curve is 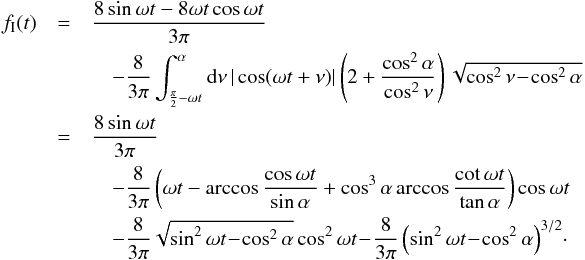 (26)For
(26)For 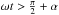 , the entire ocean is visible, and hence we need to subtract the above integral over the entire interval [−α,α ]. We find
, the entire ocean is visible, and hence we need to subtract the above integral over the entire interval [−α,α ]. We find 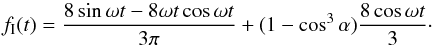 (27)For ωt>π − 2α, the glint spot is visible and a contribution fL, given by (18), must be added to the signal f. This time signal, shown Fig. 9, has a peculiar wiggle in the interval when the ocean is in full view. Clearly, the pattern function g is most useful for evaluation of the spectrum. The leading term in the large n expansion is
(27)For ωt>π − 2α, the glint spot is visible and a contribution fL, given by (18), must be added to the signal f. This time signal, shown Fig. 9, has a peculiar wiggle in the interval when the ocean is in full view. Clearly, the pattern function g is most useful for evaluation of the spectrum. The leading term in the large n expansion is 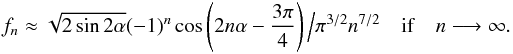 If one wishes to determine α from the Fourier peaks, and verify that the signal is from an eyeball planet, the curves in Fig. 10 can be used.
If one wishes to determine α from the Fourier peaks, and verify that the signal is from an eyeball planet, the curves in Fig. 10 can be used.
6. Saturn-like rings
Consider a Saturn-like planet, a planet with a large disk-shaped ring system. We model the ring system as a homogeneous and the thin disk in the plane with normal vector 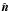 as in (2). With the inner radius b and the outer radius c, the total surface area is πc2 − πb2. We study configurations with
as in (2). With the inner radius b and the outer radius c, the total surface area is πc2 − πb2. We study configurations with 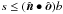 , so that the planet does not block a part of the observer’s view on the ring. Light scatters off the ring with reflectivity ℛ. For a thin disk, light can pass through so that the rings are also visibly back lit (see Porco et al. 2005). The light that comes out the other side is again scattered diffusive, with transmitivity
, so that the planet does not block a part of the observer’s view on the ring. Light scatters off the ring with reflectivity ℛ. For a thin disk, light can pass through so that the rings are also visibly back lit (see Porco et al. 2005). The light that comes out the other side is again scattered diffusive, with transmitivity 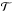 . This approach requires the disk to be optically thick (for optically thin rings, see Arnold & Schneider 2004). We factorize the net intensity F(t) for the light scattered off the ring according to
. This approach requires the disk to be optically thick (for optically thin rings, see Arnold & Schneider 2004). We factorize the net intensity F(t) for the light scattered off the ring according to 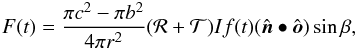 with f(t) independent of the ring absorption
with f(t) independent of the ring absorption 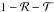 , and also with the dependence on observation direction
, and also with the dependence on observation direction 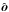 factored out, as well as the sine of the ring tilt angle β.
factored out, as well as the sine of the ring tilt angle β.
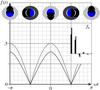 |
Fig. 11 Light curves (28), (30) from Saturn-like rings with obliquity |
Consider first the simplified case where the planet is much smaller than the ring disk, hence s ≪ c, so that the planet’s shadow is unimportant. For the interval 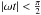 where the illuminated face has normal
where the illuminated face has normal 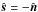 directed away from the observer and only transmitted light is visible with intensity
directed away from the observer and only transmitted light is visible with intensity 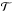 , whereas for the other half orbit, the illuminated face has
, whereas for the other half orbit, the illuminated face has 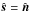 , with the scattered intensity ℛ. The phase curve for the rings is then
, with the scattered intensity ℛ. The phase curve for the rings is then 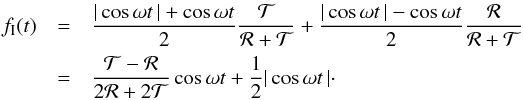 (28)The Fourier coefficients are
(28)The Fourier coefficients are 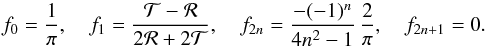 (29)The case of opaque rings, for
(29)The case of opaque rings, for 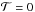 , actually produces the same signal as polar caps in the small-cap size limit α − → 0. When 0 <α ≪ β the polar cap is located inside the polar circle of latitude. The surface integral (6) is reduced to a very small circle around
, actually produces the same signal as polar caps in the small-cap size limit α − → 0. When 0 <α ≪ β the polar cap is located inside the polar circle of latitude. The surface integral (6) is reduced to a very small circle around 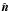 so that the factor
so that the factor 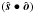 can be considered constant. The signal is a cosine function when this cap experiences polar day, and the signal is zero during polar night. This situation is opposite to the cases from Sect. 3 where we only considered α>β.
can be considered constant. The signal is a cosine function when this cap experiences polar day, and the signal is zero during polar night. This situation is opposite to the cases from Sect. 3 where we only considered α>β.
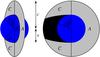 |
Fig. 12 Ringed planet, with planet radius s and outer ring radius c viewed from the direction |
6.1. Shadow cylinder
We discuss, as a final application, the situation where the planet also casts a shadow on the rings. In this case the planet itself and the shadow cast by the rings onto the planet are neglected, compare Arnold & Schneider (2004). This shadow is obviously important when the planet is not small compared to the rings. Consider the case when the planet is so large that the shadow cylinder of the planet always intersects the ring and at any time part of the ring is dark. This means that for our calculation the obliquity is bounded by 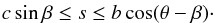 We calculate the illuminated effective area using the plane orthogonal to r. If we view the area from the position of the central star, this area is precisely the region not obscured by the planet disk. This geometry appears in Fig. 12 (on the left). We first imagine that the ring starts at the planet surface, for radii between s and c. Since the real system has radii between b and c, to obtain the required signal we must subtract the same expression with c replaced by b from this initial result. Thus consider now first a ring running from s to c. The cross section of the half of this ring that is on the dayside of the planet is
We calculate the illuminated effective area using the plane orthogonal to r. If we view the area from the position of the central star, this area is precisely the region not obscured by the planet disk. This geometry appears in Fig. 12 (on the left). We first imagine that the ring starts at the planet surface, for radii between s and c. Since the real system has radii between b and c, to obtain the required signal we must subtract the same expression with c replaced by b from this initial result. Thus consider now first a ring running from s to c. The cross section of the half of this ring that is on the dayside of the planet is 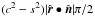 , since the dayside is fully illuminated. The illuminated part of the nightside half of the ring consists geometrically of two (identical) segments of the circle of radius c with angle φ′ projected into the outer ellipse, minus two circle segments of radius s with angle φ (see Fig. 12). Hence, φ is the angle between the point where the shadow circle of the planet crosses the outer (projected) ellipse and the direction normal to
, since the dayside is fully illuminated. The illuminated part of the nightside half of the ring consists geometrically of two (identical) segments of the circle of radius c with angle φ′ projected into the outer ellipse, minus two circle segments of radius s with angle φ (see Fig. 12). Hence, φ is the angle between the point where the shadow circle of the planet crosses the outer (projected) ellipse and the direction normal to 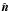 , whereas φ′ is the angle between these points for a face-on view. This yields a cross-section
, whereas φ′ is the angle between these points for a face-on view. This yields a cross-section 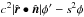 . Substitution of the point on the circle in the equation for the outer ellipse gives
. Substitution of the point on the circle in the equation for the outer ellipse gives 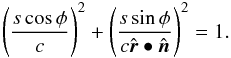 It follows that the angle is given by
It follows that the angle is given by 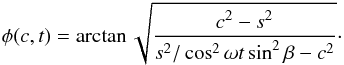 The relation between φ′ and φ is
The relation between φ′ and φ is 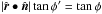 . Hence, the second angle is given by
. Hence, the second angle is given by 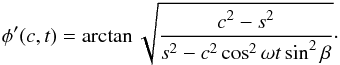 If we now add the contributions of the two ring halves, we obtain
If we now add the contributions of the two ring halves, we obtain 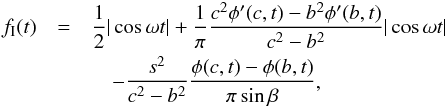 where we must remark that these equations are only valid for
where we must remark that these equations are only valid for  and
and  . This is the situation when the rings are opaque and only visible half the time. The general case is just a linear combination similar to (28). To lowest order in the axial tilt β, and for b = s, the result is simply proportional to Eq. (28), but with an extra geometric factor
. This is the situation when the rings are opaque and only visible half the time. The general case is just a linear combination similar to (28). To lowest order in the axial tilt β, and for b = s, the result is simply proportional to Eq. (28), but with an extra geometric factor 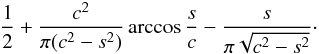 When (29) is multiplied with this same factor, the asymptotic behavior of fn for large n is accurately described for arbitrary β. For the case of maximal visibility, and arbitrary β, which is
When (29) is multiplied with this same factor, the asymptotic behavior of fn for large n is accurately described for arbitrary β. For the case of maximal visibility, and arbitrary β, which is 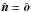 , b = s, and c = s/ sinβ, the signal from the rings simplifies to fI(t) =
, b = s, and c = s/ sinβ, the signal from the rings simplifies to fI(t) =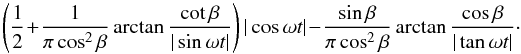 (30)The graph appears in Fig. 11. The signal is significantly weaker because for b = s, the planet shadow is large.
(30)The graph appears in Fig. 11. The signal is significantly weaker because for b = s, the planet shadow is large.
The spectrum of the signal from a planet with rings is of the form (5) and is again characterized by the fact that higher order odd coefficients are all zero. For 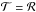 , also f1 = 0. The dominant Fourier coefficient of (30) is a relatively short formula,
, also f1 = 0. The dominant Fourier coefficient of (30) is a relatively short formula, 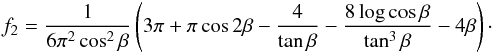 The Fourier peaks for rings behave asymptotically as (− 1)n + 1n-2 like (29), whereas for the planets the tail behaves as n-4 like (16). This behavior allows one to discriminate between the signal from a thin disk and a sphere.
The Fourier peaks for rings behave asymptotically as (− 1)n + 1n-2 like (29), whereas for the planets the tail behaves as n-4 like (16). This behavior allows one to discriminate between the signal from a thin disk and a sphere.
7. Conclusions
When a planetary system is observed continuously over a number of years, the Fourier transform of the light signal provides a natural method of analysis. The immediate advantages are: (i) the glare from the host star (in observations for large planets near M-dwarfs without an occultor), or some residual glare, can be filtered out. Stellar noise at the orbital frequencies swamps the Fourier peaks for small s2/r2. (ii) Atmospheric cloud cover that partially obscures the surface, is also partially filtered out, if clouds mainly contribute an a-periodic component in the signal. (iii) Well-defined orbital and diurnal frequencies (see Pallé et al. 2008) can be obtained from the peak-center positions. (iv) Contributions of different planets can be identified, provided they are not in orbital resonance. (v) The asymptotic behavior of the peak-amplitudes, phase factors, and even-odd structure allows us to separate out and identify different contributions (reflective oceans, land or ice sheets, or rings) in the light signal. (vi) For observation time T of N orbits, the signal-to-noise ratio in the peaks is enhanced by the root of N, essentially because the Fourier transform is an averaging method.
How can one distinguish between planets with or without rings and identify the different configurations we consider here? Since none of the specific parameters are known in advance, one has to rely on general properties of a measured Fourier spectrum. To apply our results, an astronomer should first identify the spectral peaks from the intensity spectrum of a star system that belong to a single planet. If sidebands to the annual nω-peak pattern (a similar pattern shifted by Ω and 2Ω, etc.) are not found, either the planet is banded and has no longitudinal pattern, or the planet is tidally locked (so that Ω = ω). Then the astronomer needs to fix the orbital phase with respect to the inferior conjunction. For a transiting planet, this is at moment of transit (peaking).
If the coefficients are all positive and decay as fn ~ n-2, this may indicate ocean glint, see Eq. (19). If there are no higher-order odd peaks, f2n + 1 = 0, then there is no glint, which implies that the point of specular reflection is on land or behind a thick atmosphere, see Eq. (11). When the glint spot abruptly moves from ocean to a polar cap or back, this generally occurs when the glint effect is weak. We therefore expect that the n-1 behavior due to such a discontinuous jump will only dominate in the far-end regions of the tail that cannot be resolved. If the spectrum (after subtracting any observed glint component) has an alternating even tail behaving as f2n ~ (−1)n + 1n-2, the signal is that of a scattering disk, either from a flat polar-cap (inside the polar circle) or from a ringed system. The value of f1 can determine if the signal is light scattered by semitransparent rings, see Eq. (28). The peaks of an locked planet with a circular ocean decay in strength as | fn | ~ n−7/2. A generic Lambertian signal from a planet decays fast as f2n ~ n-4. If we assume a stellar-noise level of 10-3, the number of peaks that is expected to be resolved is about 100, 30, 10, and 6, for a perfect glint spike, rings, and Lambertian scattering ice caps, respectively. If the photometry is not good enough to detect the fraction 10-3 of the average planet luminosity, of the order s2I/ 4r2, then fewer peaks can be found.
For observation that is not edge on the orbital plane, the spectrum obtains an extra factor of sin2nθ. This exponential decay will limit the number of peaks that can be resolved, which will hamper identification. The effect of orbit eccentricity, see Eq. (B.1) is also exponentially weak because fn ~ (ϵe/2)n. This effect dominates only for zero inclination, and in case obliquity is zero or the planet is homogeneous (or at least the exposed region is). Any other periodic signal is caused by changing phases or rotating patterns on the planet surface. The expressions at the end of Sects. 4.1–4.2 for g1, g2 are
simple enough to see whether the four parameters, θ,φ,α,β, for a water world with polar caps fit the observation of the first two Fourier peaks.
If one isolated peak appears in the spectrum, this could indicate a homogeneous but large planet at such a small inclination that all other peaks are suppressed. However, if all the reflected light comes from a circle around the (north or south) pole that happens to be in full view, a pure cosine light curve is precisely what will be observed for a planet with zero axial tilt, see Sect. 4.3. A bright circularly symmetric albedo map around a planet’s pole on a further absorbing surface, could indicate an exposed circular polar ice cap surrounded by oceans.
The main disadvantage of the Fourier transform is the need for many periods, hence a long continuous observation (in the optical range), but we think that it would still be worthwhile to single out a promising exoplanetary system as a candidate for study of the intensity spectrum.
Online material
Appendix A: Transits and observation gaps
When planet transits and reflected light curves are observed in one signal, large amplitudes from the periodic transits are added on top of the weak reflection peaks. For Jupiters near dwarf stars, it may still be possible to separate the two components in the signal.
Observing from direction  , one sees a planet passing in front of the star disk for
, one sees a planet passing in front of the star disk for  . The transits are thus found (taking φ = 0 for convenience, and r ≪ S, and
. The transits are thus found (taking φ = 0 for convenience, and r ≪ S, and  ) in t-intervals for which
) in t-intervals for which  Then the measured signal dips by − s2I0/S2 (which is − 10-4I0 for a twin earth). We are interested in the reflected signal from a planet. This is a factor S2/ 4r2 weaker (10-6) than a transit signal and s2/ 4r2 weaker (10-10) than the star. For a Jupiter close to a dwarf star, these ratios are much more practical than for an Earth-twin, and it may not be necessary to block the star.
Then the measured signal dips by − s2I0/S2 (which is − 10-4I0 for a twin earth). We are interested in the reflected signal from a planet. This is a factor S2/ 4r2 weaker (10-6) than a transit signal and s2/ 4r2 weaker (10-10) than the star. For a Jupiter close to a dwarf star, these ratios are much more practical than for an Earth-twin, and it may not be necessary to block the star.
Although the transit signal is of short duration (minutes), the combined signal can be detected continuously (for years). Consider the Fourier series of a rapid transit: 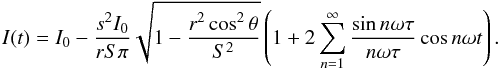 (A.1)The short duration of the eclipse gives rise to peak amplitudes of a fraction s2/rS of I0 (of the order 10-7I0). The Fourier coefficients of the transit signal are
(A.1)The short duration of the eclipse gives rise to peak amplitudes of a fraction s2/rS of I0 (of the order 10-7I0). The Fourier coefficients of the transit signal are 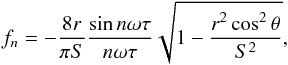 (A.2)which are of the order r/S compared to the coefficients in the phase signal, which are of order 1. In other words, in the Fourier spectrum, the reflected signal is about a factor S/r weaker (10-3) than the transit signal. To observe the phase part in a combined phase-plus-transit signal, the noise from the transit must be less than the phase peak amplitudes. Our Sun has noise levels of 10-5 at (transit-frequencies of) 10-5 Hz, and a noise level 10-3 for (orbital frequencies) 10-6 Hz, see Aigrain et al. (2004), so the large transit component does indeed pose a problem since the absolute noise will be large. Of course, when a planet is periodically blocking its star, the star is also blocking the planet every other half period. The corresponding dip in the signal is again a factor S/r smaller.
(A.2)which are of the order r/S compared to the coefficients in the phase signal, which are of order 1. In other words, in the Fourier spectrum, the reflected signal is about a factor S/r weaker (10-3) than the transit signal. To observe the phase part in a combined phase-plus-transit signal, the noise from the transit must be less than the phase peak amplitudes. Our Sun has noise levels of 10-5 at (transit-frequencies of) 10-5 Hz, and a noise level 10-3 for (orbital frequencies) 10-6 Hz, see Aigrain et al. (2004), so the large transit component does indeed pose a problem since the absolute noise will be large. Of course, when a planet is periodically blocking its star, the star is also blocking the planet every other half period. The corresponding dip in the signal is again a factor S/r smaller.
The effect of discontinuous but periodic observation gaps on the Fourier peaks is different from that of a transit. For observation gaps, the continuous signal is multiplied with a periodic function, which is zero for the intervals sin | ωt | < sinωτ, whereas for a transit, such a function is added instead. Periodic interruptions at the inferior and major conjunction are inevitable for an edge-on observation, when the planet passes behind an occulter or within the telescope’s inner working angle. The blocking durations 2τ must obviously be short (compared to the period). In the short-gaps limit, the multiplicative function becomes 1−2ωτ ∑ e2inωt/π. The even and odd peaks, f2n and f2n + 1 are shifted by (∓ f(0) − f(π/ω))ωτ/π, in the approximation nωτ ≪ 1.
Appendix B: Kepler orbits
 |
Fig. B.1 Phase-light curves for top view on an eccentric planetary orbit. Values for the eccentricity are ϵ = 0 (gray), ϵ = .1 (blue), .2 (black), and .3 (purple, highest peak intensity). The visuals and the inset are for ϵ = .2. |
For planets with noncircular, but eccentric orbits, the distance to the host star is a time-varying periodic function. As a result, the light intensity received by the planet is periodically modulated. We will calculate here the effect of (small) orbital eccentricity on phase light curves. The position vector is no longer given by the circle (1) but with an ellipse with a semimajor axis a along the x-direction and eccentricity ϵ, given by 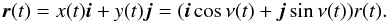 The Cartesian coordinates (x,y,z) = (x,y,0) are
The Cartesian coordinates (x,y,z) = (x,y,0) are 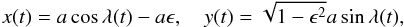 and the polar coordinates
and the polar coordinates 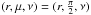 are given by
are given by 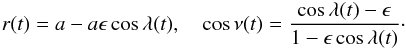 These orbital coordinates are expressed in the eccentric anomaly λ (usually denoted E, see Goldstein 1964). This parameter λ is (implicitly) defined as a function of the orbital phase ωt, from
These orbital coordinates are expressed in the eccentric anomaly λ (usually denoted E, see Goldstein 1964). This parameter λ is (implicitly) defined as a function of the orbital phase ωt, from 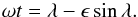 An expansion in ϵ for the coordinates in the time variable can be obtained with
An expansion in ϵ for the coordinates in the time variable can be obtained with  In the general case, the eccentricity of the orbit leads to a modulation factor a2/r2(t) in the light curve. The simplest case arises for a homogeneous planet with inclination θ = 0. (Taking MI = 1, ϵ = 0, the half-illuminated disk gives
In the general case, the eccentricity of the orbit leads to a modulation factor a2/r2(t) in the light curve. The simplest case arises for a homogeneous planet with inclination θ = 0. (Taking MI = 1, ϵ = 0, the half-illuminated disk gives 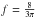 , neglecting the possible 45 degrees glint effect.) The signal is
, neglecting the possible 45 degrees glint effect.) The signal is 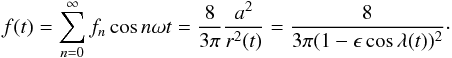 The graph appears in Fig. B.1. Note that Mercury has ϵ = .2.
The graph appears in Fig. B.1. Note that Mercury has ϵ = .2.
We calculate the Fourier coefficients fn by first considering the function 1 /r(t). We use λ as integration variable and require for this substitution 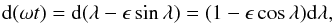 so that
so that 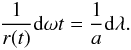 When the complex harmonic einωt is expressed as a periodic function of λ, one obtains the generating function for the Bessel functions (of the first kind)
When the complex harmonic einωt is expressed as a periodic function of λ, one obtains the generating function for the Bessel functions (of the first kind) 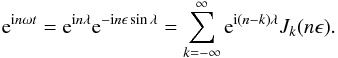 Combining the last two identities and integrating over a full period gives us the Fourier coefficients for 1 /r(t), which are
Combining the last two identities and integrating over a full period gives us the Fourier coefficients for 1 /r(t), which are 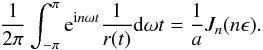 Hence, the reciprocal distance has Fourier series
Hence, the reciprocal distance has Fourier series 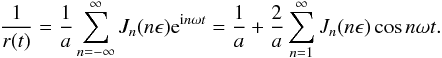 We used J− n(−nϵ) = Jn(nϵ) to get the last identity. It is interesting that the Fourier coefficients of r(t) and of cosθ(t) are Bessel functions, although the functions r(t) and cosθ(t) themselves have no explicit expression in t. The Fourier coefficients of the all powers rN(t), with N ≥ −1 of the radial coordinate r(t) are finite combinations of Bessel functions too.
We used J− n(−nϵ) = Jn(nϵ) to get the last identity. It is interesting that the Fourier coefficients of r(t) and of cosθ(t) are Bessel functions, although the functions r(t) and cosθ(t) themselves have no explicit expression in t. The Fourier coefficients of the all powers rN(t), with N ≥ −1 of the radial coordinate r(t) are finite combinations of Bessel functions too.
The luminosity of a planet is, however, inversely proportional to the square of the distance r(t). We may use the
convolution the series for 1 /r(t) with itself to obtain  Alternatively we may write
Alternatively we may write 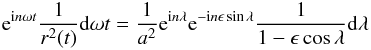 and use the series
and use the series 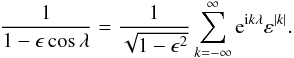 The parameter ε is a new measure of the orbital eccentricity (also in the interval [ 0,1 ]) defined with
The parameter ε is a new measure of the orbital eccentricity (also in the interval [ 0,1 ]) defined with 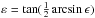 . We may obtain a second way to express the Fourier series
. We may obtain a second way to express the Fourier series  We can now pick out the Fourier coefficients of the light curve. They are, for n ≥ 1,
We can now pick out the Fourier coefficients of the light curve. They are, for n ≥ 1, 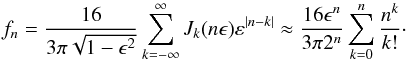 (B.1)The second, approximate equality contains the lowest-order contributions in ϵ. The finite sum is the Taylor polynomial of degree n for the function exp(n). Therefore the coefficients drop to zero exponentially if ϵ< 2/e, as fn ~ ϵnen/ 2n.
(B.1)The second, approximate equality contains the lowest-order contributions in ϵ. The finite sum is the Taylor polynomial of degree n for the function exp(n). Therefore the coefficients drop to zero exponentially if ϵ< 2/e, as fn ~ ϵnen/ 2n.
Since Earth-like planets with a stable water-ice equilibrium will not likely occur for orbits that are too eccentric, we are mainly interested at low values of ϵ. With the above equations it is possible to express the sine components as linear combinations in ϵ of the cosine components for exact circular orbits.
References
- Aigrain, S., Favata, F., & Gilmore, G. 2004, A&A, 414, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnold, L., & Schneider, J. 2004, A&A, 420, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedict, G., McArthur, B., Forveille, T., et al. 2002, ApJ, 581, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W., Koch, D., Jenkins, J., et al. 2009, Science, 325, 709 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Catala, C. 2009, Exp. Astron., 23, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N., & Agol, E. 2008, ApJ, 678, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N., Agol, E., Meadows, V., et al. 2009, ApJ, 700, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N., Abbot, D., & Voigt, A. 2012, ApJ, 752, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N., Fuentes, P., & Haggard, H. 2013, MNRAS, 434, 2465 [NASA ADS] [CrossRef] [Google Scholar]
- Dyudina, A., Sackett, P., Bayliss, D., et al. 2005, ApJ, 618, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Fairchild, I., & Kennedy, M. 2007, J. Geol. Soc., 164, 895 [CrossRef] [Google Scholar]
- Ford, E., Seager, S., & Turner, E. 2001, Nature, 412, 885 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fujii, Y., & Kawahara, H. 2012, ApJ, 755, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Gaulme, P., Vannier, M., Guillot, T., et al. 2010, A&A, 518, L153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldstein, H. 1964, Classical Mechanics, ninth Dover printing, tenth GPO printing edn. (New York, Dover) [Google Scholar]
- Greaves, J., Holland, W., Wyatt, M., et al. 2005, ApJ, 619, L187 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D., Matthews, J., Seager, S., & Kuschnig, R. 2003, ApJ, 597, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Hecht, E. 2002, Optics, fourth edn. (San Fransisco: Addison-Wesley) [Google Scholar]
- Hidas, M. G., Ashley, M. C. B., Webb, J. K., et al. 2005, MNRAS, 360, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, P., Kaufman, A., Halverson, G., & Schrag, D. 1998, Science, 281, 1342 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, Y., & Yang, J. 2014, PNAS, 111, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Lean, J. 2000, Geophys. Res. Lett., 27, 2425 [CrossRef] [Google Scholar]
- Macdonald, F., Schmitz, M., Crowley, J., et al. 2010, Science, 327, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Oakley, P., & Cash, W. 2009, ApJ, 700, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Pallé, A. Ford, E. Seager, S. Montañés Rodríguez, P., & Vazquez, M. 2008, ApJ, 676, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Pierrehumbert, R. 2011, ApJ, 726, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C., Baker, E., Barbara, J., et al. 2005, Science, 307, 1226 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Robinson, T., Meadows, V., & Crisp, D. 2010, ApJ, 721, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I., de Mooij, E., & Albrecht, S. 2009, Nature, 459, 543 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stam, D., De Rooij, W., Cornet, G., & Hovenier, J. 2006, A&A, 452, 669 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Steffen, J., Fabrycky, D., Ford, E., et al. 2012, MNRAS, 421, 2342 [NASA ADS] [CrossRef] [Google Scholar]
- van Hulst, H. 1980, Multiple Light Scattering: Tables, Formulas, and Applications, Vols. 1 and 2 (New York: Academic Press) [Google Scholar]
- Vokroughlicky, D., & Farinella, P. 1995, A&A, 298, 307 [NASA ADS] [Google Scholar]
- Welsh, W., Orosz, J., Seager, S., et al. 2010, ApJ, 713, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, D., & Gaidos, E. 2008, Icarus, 195, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Zugger, M., Kasting, J., Williams, D., Kane, T. J., & Philbrick, C. 2010, ApJ, 723, 1168 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Standard light curve (15) for a homogeneous (Lambertian) planet: normalized intensity f versus orbital phase ωt, for edge-on observation. The inset shows, to scale, the coefficients gn which are proportional to fn (16) according to (11). |
| In the text | |
 |
Fig. 2 Harmonic ratios g2/g1 (blue), g4/g1 (purple) and g6/g1 (orange) for a snowball planet, versus inclination angle θ. These curves can be used to determine the inclination θ or to conclude that the planet is, instead, inhomogeneous. |
| In the text | |
 |
Fig. 3 Standard Fresnel light curve (18) from ocean glint for edge-on view (in blue; the Lambertian scattering signal is shown for comparison in gray). The inset shows the spectrum. In the visuals, the glint is yellow. |
| In the text | |
 |
Fig. 4 Harmonic ratios f5/f3 (blue), f7/f3 (purple), and f9/f3 (orange) for a planet with permanent ocean glint. The glint spot of a water world with polar caps is continuously visible for |
| In the text | |
 |
Fig. 5 Light curve of planet with polar caps for edge-on observation, |
| In the text | |
 |
Fig. 6 Light curve of planet with polar caps for edge-on observation, |
| In the text | |
 |
Fig. 7 Light curve for planet with polar caps for inclined observation |
| In the text | |
 |
Fig. 8 Polar-cap light curve (25) for top view; inclination θ = 0. Cap extension is |
| In the text | |
 |
Fig. 9 Light curve (26), (27) for an eyeball planet with circular ocean extending over α = π/ 4, with and without glint (blue and black), as given in Eq. (18). The view is edge-on. The snowball light curve (gray) is for comparison. |
| In the text | |
 |
Fig. 10 Peak ratios f1/f0 (black), f2/f0 (blue), f3/f0 (purple), and f4/f0 (orange) for an eyeball planet viewed edge-on plotted as a function of the ocean extension angle α. Ocean glint is neglected. |
| In the text | |
 |
Fig. 11 Light curves (28), (30) from Saturn-like rings with obliquity |
| In the text | |
 |
Fig. 12 Ringed planet, with planet radius s and outer ring radius c viewed from the direction |
| In the text | |
 |
Fig. B.1 Phase-light curves for top view on an eccentric planetary orbit. Values for the eccentricity are ϵ = 0 (gray), ϵ = .1 (blue), .2 (black), and .3 (purple, highest peak intensity). The visuals and the inset are for ϵ = .2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.