| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201424340 | |
| Published online | 15 July 2015 | |
Online material
Appendix A: Direct computation of the monodromy
In the main body of this paper, we computed the monodromy through the trick of identifying places of known phase in the data and drawing the closed curve through those places. We drew lines along contiguous places of known phase in the crests or the valleys of the waves on both sides of the suspected dislocation and joined them with a straight line that crossed an integer amount of the crests or valleys. This method was suggested by the organized patterns in the data that allowed an easy and safe identification of those places of known phase. But to feel fully confident about the method and the presence of the dislocation, we would prefer to be able to directly solve the monodromy integral along any closed curve in a general wave field.
The observed data in our present case is the Doppler shift of an emission line interpreted as the line-of-sight velocity of the plasma. This is a real quantity. Our first step will be to interpret these observations as the real part of a complex wave field for which we have to determine the imaginary part. For simplicity we assume that the observation can be safely interpreted as due to a wave with a unique average frequency ω. We can describe the observed wave field as
![]() The observations, which is the real quantity φ at each position (z,t), are described as a variable real amplitude A(z,t) times a cosine variation in time with frequency ω. We asume a constant zero time for the full wave field, but allow for a local phase shift α(z,t) that, through its time dependence, may include local frequency changes. The combination of the variable amplitude and local phase shifts allows describing very complicated wave patterns, including the one in Fig. 2, as long as one accepts the constant average frequency ω over the time and place of the observation.
The observations, which is the real quantity φ at each position (z,t), are described as a variable real amplitude A(z,t) times a cosine variation in time with frequency ω. We asume a constant zero time for the full wave field, but allow for a local phase shift α(z,t) that, through its time dependence, may include local frequency changes. The combination of the variable amplitude and local phase shifts allows describing very complicated wave patterns, including the one in Fig. 2, as long as one accepts the constant average frequency ω over the time and place of the observation.
We can decompose the cosine function as
![]() The local phase shift α can now be interpreted as a local modification of the amplitude of two different waves:
The local phase shift α can now be interpreted as a local modification of the amplitude of two different waves: 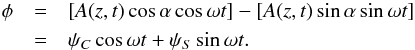 This suggests the construction of the complex wave field
This suggests the construction of the complex wave field
![]() which is the amplitude of the observed wave, while locally it adds a phase χ
which is the amplitude of the observed wave, while locally it adds a phase χ
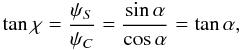 which is identical to the local phase of the observed wave. Thus the proposed complex wave field
which is identical to the local phase of the observed wave. Thus the proposed complex wave field
![]() has the same observable parameters as the original real wave φ(z,t) and can be used instead of it, with a straightforward (diffeomorphic) correspondence between them.
has the same observable parameters as the original real wave φ(z,t) and can be used instead of it, with a straightforward (diffeomorphic) correspondence between them.
Since z and t are the coordinates of Fig. 2, we rewrite this complex field for the wave on the longitudinal velocity as just a real amplitude and a phase
![]() After differentiating this expression, we find that
After differentiating this expression, we find that ![]() (A.1)Dividing by ψ
(A.1)Dividing by ψ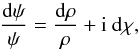 (A.2)we can integrate both sides of this last expression along a closed curve C, the monodromy:
(A.2)we can integrate both sides of this last expression along a closed curve C, the monodromy:
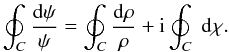 Since ρ, the amplitude of the complex wave, is, by definition, a real quantity, we find that
Since ρ, the amplitude of the complex wave, is, by definition, a real quantity, we find that ![]() on any closed curve, and the monodromy simplifies to
on any closed curve, and the monodromy simplifies to 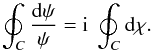 (A.3)The righthand part is the monodromy over the phase of the wave, which if different than zero, identifies the presence of a singularity, a dislocation, inside the closed curve. The lefthand part is an integral over the observed data. We conclude that from the observations, we can build a complex field ψ and then compute the integral on the left along the chosen closed path C to obtain the required integral over the phase on the right. This solves the problem of computing the monodromy on the phase directly from the data. It is useful to make one further step. The integral on the lefthand side can be formally integrated
(A.3)The righthand part is the monodromy over the phase of the wave, which if different than zero, identifies the presence of a singularity, a dislocation, inside the closed curve. The lefthand part is an integral over the observed data. We conclude that from the observations, we can build a complex field ψ and then compute the integral on the left along the chosen closed path C to obtain the required integral over the phase on the right. This solves the problem of computing the monodromy on the phase directly from the data. It is useful to make one further step. The integral on the lefthand side can be formally integrated 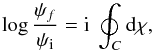 (A.4)where ψf and ψi are the final and initial values, respectively, of ψ at the closed path. These would be the same, since the path is closed, except that the ψ function is complex. This raises the possibility of those initial and final values not being in the same Riemann surface of the logarithm function. Indeed, the complex logarithm2 is log z = (log z)principal + i2πN. The principal value of the logarithm is identical for the initial and final points, so that we can conclude that
(A.4)where ψf and ψi are the final and initial values, respectively, of ψ at the closed path. These would be the same, since the path is closed, except that the ψ function is complex. This raises the possibility of those initial and final values not being in the same Riemann surface of the logarithm function. Indeed, the complex logarithm2 is log z = (log z)principal + i2πN. The principal value of the logarithm is identical for the initial and final points, so that we can conclude that 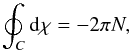 (A.5)where N is the number of twists made by the logarithm function as it follows the path C.
(A.5)where N is the number of twists made by the logarithm function as it follows the path C.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


