| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201425468 | |
| Published online | 04 June 2015 | |
Online material
Appendix A: Energy in slow wave modes in thin flux tubes
We now focus on the energy expressions for slow waves in thin flux tubes, i.e. with a small but non-zero value of kR. As in Sect. 3.1 we find that as kR → 0 the frequency of slow modes is given by ω = ωT,i ± (kR)2ln(kR)ω1, where the “plus” is the fundamental body mode and the “minus” is the surface mode. We have the same expressions for niR, κeR, and ω1 as in Sect. 3.1 and so we do not list them here. To calculate the amplitudes Ai and Ae we take some extra terms from the Bessel function expansions into account. We know that  where there are some extra terms from the Bessel function expansions. In the first line the “plus” indicates surface modes, while the “minus” indicates the fundamental body mode. To calculate the energy inside the flux tube (Eqs. (15)and (17)) we also need to approximate some products of Bessel functions, i.e.
where there are some extra terms from the Bessel function expansions. In the first line the “plus” indicates surface modes, while the “minus” indicates the fundamental body mode. To calculate the energy inside the flux tube (Eqs. (15)and (17)) we also need to approximate some products of Bessel functions, i.e. 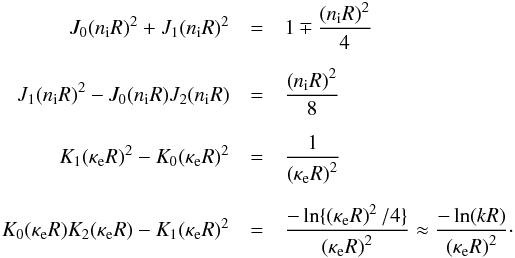 In the first line the “minus” indicates the fundamental body mode, while the “plus” indicates surface modes. These expansion can all be checked in Abramowitz & Stegun (1972). We now have all the ingredients needed to calculate the energy in slow sausage wave modes in thin flux tubes. The energy inside the flux tube is given by
In the first line the “minus” indicates the fundamental body mode, while the “plus” indicates surface modes. These expansion can all be checked in Abramowitz & Stegun (1972). We now have all the ingredients needed to calculate the energy in slow sausage wave modes in thin flux tubes. The energy inside the flux tube is given by  (A.1)where we have kept all terms of order (kR)2 or lower. The “minus” indicates the fundamental body mode, while the “plus” indicates surface modes. We notice the equipartition between kinetic and potential (i.e. the sum of both magnetic and thermal energy) energy. The energy outside the flux tube (Eqs. (19)) can also be calculated and we find
(A.1)where we have kept all terms of order (kR)2 or lower. The “minus” indicates the fundamental body mode, while the “plus” indicates surface modes. We notice the equipartition between kinetic and potential (i.e. the sum of both magnetic and thermal energy) energy. The energy outside the flux tube (Eqs. (19)) can also be calculated and we find 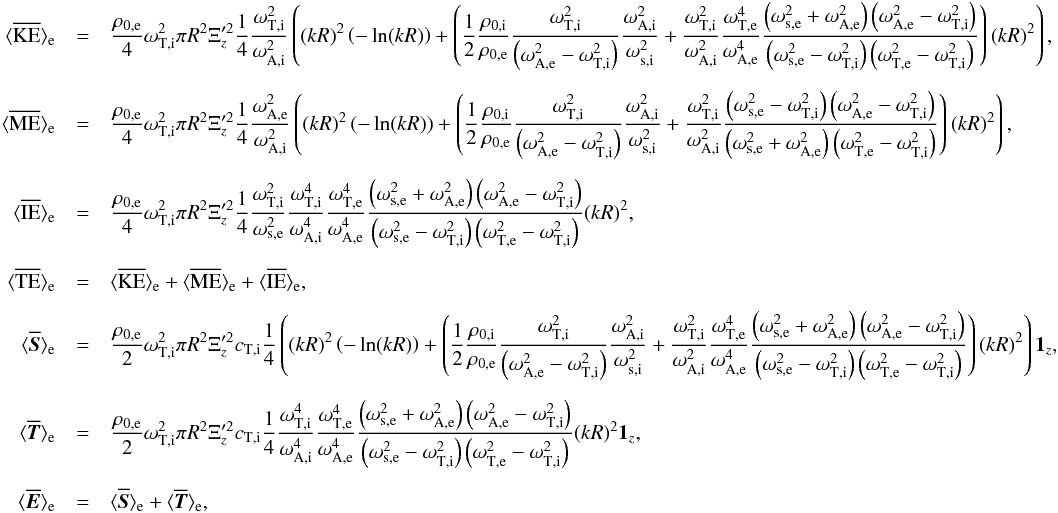 (A.2)where again we have kept all terms of order (kR)2 or lower. The dominant term in these energy equations is the (kR)2( − ln(kR)) term. This shows that we do not find equipartition in this case since the coefficients in the kinetic and magnetic energy before the (kR)2( − ln(kR)) term are not the same. This puzzling result was further investigated numerically. We used different equilibrium parameters with different small values of kR. We discovered a small error in the equipartition of energy of the order of 10-5 of the total energy. When using the full set of equations to calculate the energy (i.e. Eqs. (17)and (19)) we did find equipartition between kinetic and potential energy. This clearly shows that there is indeed equipartition, but approximating the Bessel functions has introduced a small error.
(A.2)where again we have kept all terms of order (kR)2 or lower. The dominant term in these energy equations is the (kR)2( − ln(kR)) term. This shows that we do not find equipartition in this case since the coefficients in the kinetic and magnetic energy before the (kR)2( − ln(kR)) term are not the same. This puzzling result was further investigated numerically. We used different equilibrium parameters with different small values of kR. We discovered a small error in the equipartition of energy of the order of 10-5 of the total energy. When using the full set of equations to calculate the energy (i.e. Eqs. (17)and (19)) we did find equipartition between kinetic and potential energy. This clearly shows that there is indeed equipartition, but approximating the Bessel functions has introduced a small error.
When taking the long wavelength limit (i.e. kR = 0) we find that Eqs. (A.1)and (A.2)simplify to Eqs. (24)as expected.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


