| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 15 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201425446 | |
| Published online | 14 April 2015 | |
Online material
Appendix A: Unperturbed disk state
Before we consider the equations describing the 3D formulation of Ogilvie (2008) for the one-armed oscillation model, we shall note the fundamental equations describing the unperturbed disk. The model adopted here is the same as that detailed in ZT II (their Sect. 2). We assume a steady, axisymmetric viscous decretion disk, for which the surface density is given by (Bjorkman & Carciofi 2005)  (A.1)where ϖ = (x2 + y2)1/2 is the horizontal distance from the center of the star, ⟨ μ ⟩ is the average mean molecular weight, mH is the mass of the hydrogen atom, α is the viscosity parameter of Shakura & Sunyaev (1973), ⟨ T ⟩ is the average gas kinetic temperature, Ṁ is the stellar decretion rate, and R0 is an arbitrary integration constant.
(A.1)where ϖ = (x2 + y2)1/2 is the horizontal distance from the center of the star, ⟨ μ ⟩ is the average mean molecular weight, mH is the mass of the hydrogen atom, α is the viscosity parameter of Shakura & Sunyaev (1973), ⟨ T ⟩ is the average gas kinetic temperature, Ṁ is the stellar decretion rate, and R0 is an arbitrary integration constant.
The mass-decretion rate Ṁ is related to the radial velocity via the equation of continuity (Carciofi & Bjorkman 2008). It is given by ![]() (A.2)where vϖ is the vertically-averaged, radial velocity.
(A.2)where vϖ is the vertically-averaged, radial velocity.
In binaries with low eccentricities, the Be disk is expected to be truncated by the tidal torques from the companion (Okazaki & Negueruela 2001). For a circular binary with a small mass ratio (q = M2/M1 ≲ 0.3), such as ζ Tau, the truncation takes place at the tidal radius, which is approximately given by 0.9RRoche (Whitehurst & King 1991), with RRoche being the Roche radius approximately given by (Eggleton 1983)  (A.3)where a is the semi-major axis.
(A.3)where a is the semi-major axis.
We also assume that the unperturbed disk is in hydrostatic balance in the vertical direction. Then, the unperturbed density is given by  (A.4)where ρm(ϖ) is the disk density at the mid-plane (z = 0), and the disk scale height is given by
(A.4)where ρm(ϖ) is the disk density at the mid-plane (z = 0), and the disk scale height is given by  (A.5)where He ≡ (k ⟨ T ⟩ Re)1/2( ⟨ μ ⟩ mHGM)− 1/2 is the disk scale height at the inner radius ϖ = Re.
(A.5)where He ≡ (k ⟨ T ⟩ Re)1/2( ⟨ μ ⟩ mHGM)− 1/2 is the disk scale height at the inner radius ϖ = Re.
We can find the radial dependence of the midplane density by integrating ρ in the z direction:  (A.6)From Eqs. (A.1) to (A.6), we have
(A.6)From Eqs. (A.1) to (A.6), we have 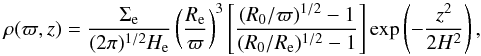 (A.7)where Σe is the surface density at the inner disk radius, which is written as
(A.7)where Σe is the surface density at the inner disk radius, which is written as 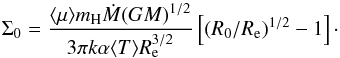 (A.8)
(A.8)
Appendix B: 3D Structure of m = 1 oscillations in truncated decretion disks
On the unperturbed state described in Appendix A, we superpose a linear m = 1 perturbation in the form of a normal mode of frequency ω, which varies as exp [i(ωt − φ)]. For simplicity, we assume the perturbation to be isothermal. The linearized perturbed equations are then obtained as follows: 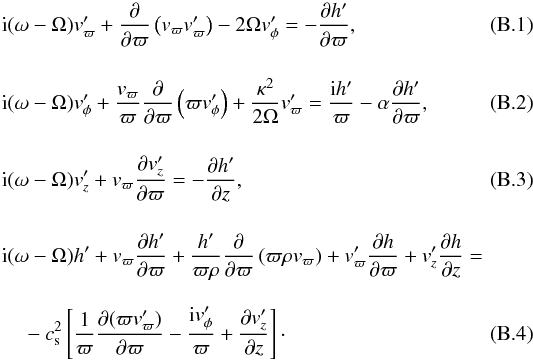 Here cs = (k ⟨ T ⟩ /μmH)1/2 is the isothermal sound speed and (
Here cs = (k ⟨ T ⟩ /μmH)1/2 is the isothermal sound speed and (![]() ) the perturbed velocity;
) the perturbed velocity; ![]() and
and ![]() are respectively the unperturbed and perturbed enthalpy, where ρ′ is the density perturbation.
are respectively the unperturbed and perturbed enthalpy, where ρ′ is the density perturbation.
Following the formulation made by Ogilvie (2008, see also Oktariani & Okazaki 2009, in order to take the 3D effect into account, we must expand perturbed quantities in the z-direction in terms of Hermite polynomials: 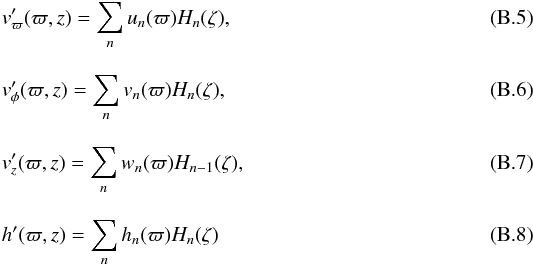 (Ogilvie 2008; see also Okazaki et al. 1987), where Hn(ζ) is the Hermite polynomial defined by
(Ogilvie 2008; see also Okazaki et al. 1987), where Hn(ζ) is the Hermite polynomial defined by 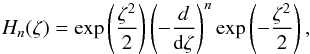 (B.9)with ζ = z/H and n being a dimensionless vertical coordinate and a non-negative integer, respectively. We note that wn = 0 for n = 0.
(B.9)with ζ = z/H and n being a dimensionless vertical coordinate and a non-negative integer, respectively. We note that wn = 0 for n = 0.
Replacing the perturbed quantities by their Hermite polynomials expansion, Eqs. (B.1) to (B.4) become 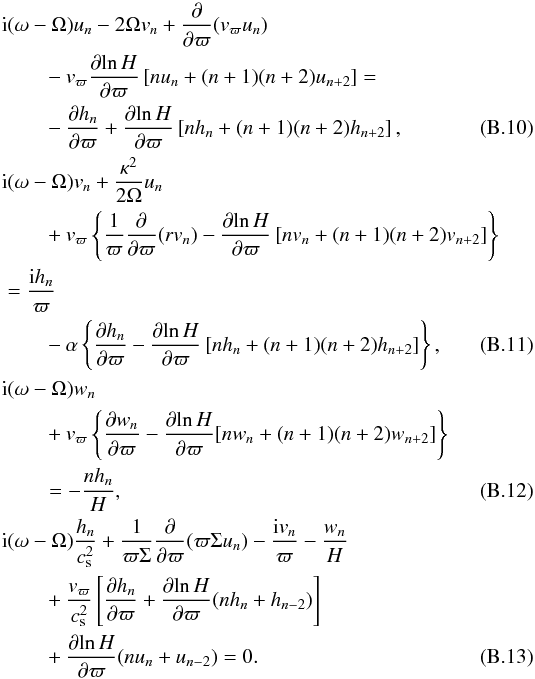 We note that Eqs. (B.10)−(B.13) are reduced to Eqs. (48)–(51) of Ogilvie (2008) provided that the effects of the radial velocity vϖ and viscosity α are neglected and i is replaced with −i2.
We note that Eqs. (B.10)−(B.13) are reduced to Eqs. (48)–(51) of Ogilvie (2008) provided that the effects of the radial velocity vϖ and viscosity α are neglected and i is replaced with −i2.
Still following Ogilvie (2008), we close the system of resulting equations by assuming un ≡ 0 for n ≥ 2. Using the approximations | ω | ≪ Ω, | Ω − κ | ≪ Ω, (cs/ϖΩ)2 ≪ 1, and vϖ ≪ rΩ, the basic equations for linear m = 1 perturbations in viscous decretion disks are then 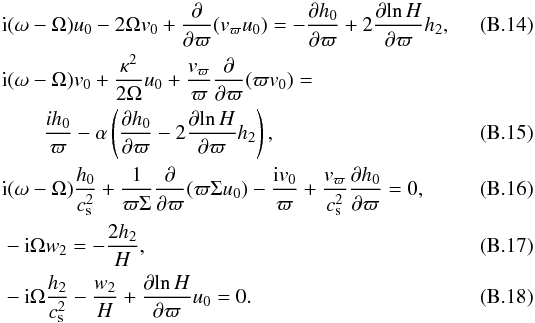 Eliminating w2 and h2 from Eqs. (B.14)−(B.18), we obtain a set of three equations for h0, u0, and v0:
Eliminating w2 and h2 from Eqs. (B.14)−(B.18), we obtain a set of three equations for h0, u0, and v0: 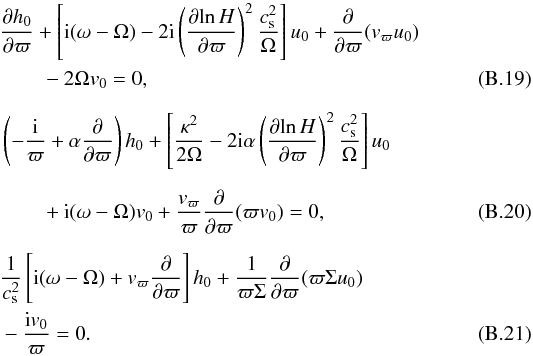 Equations (B.19), (B.20), and (B.21) correspond respectively to Eqs. (16), (17), and (15) from ZT II. They are solved with the same boundary conditions, i.e., a rigid wall (u0,v0) = 0 at the inner disk radius and Δp = 0 at the outer disk radius, Δp being the Lagrangian perturbation of pressure.
Equations (B.19), (B.20), and (B.21) correspond respectively to Eqs. (16), (17), and (15) from ZT II. They are solved with the same boundary conditions, i.e., a rigid wall (u0,v0) = 0 at the inner disk radius and Δp = 0 at the outer disk radius, Δp being the Lagrangian perturbation of pressure.
We note that the terms ![]() (
(![]() in isothermal disks) in Eq. (B.19) and
in isothermal disks) in Eq. (B.19) and ![]() in Eq. (B.20) result from the 3D effect and provides an important contribution to the confinement of the m = 1 modes. The other terms are the same as in the basic equations used in ZT II.
in Eq. (B.20) result from the 3D effect and provides an important contribution to the confinement of the m = 1 modes. The other terms are the same as in the basic equations used in ZT II.
Once Eqs. (B.19)−(B.21) are solved, the second-order terms, w2 and h2, are obtained from Eqs. (B.17) and (B.18),  where cs = ΩH. Finally, under the closure approximation adopted here, the perturbed density and velocity are given by
where cs = ΩH. Finally, under the closure approximation adopted here, the perturbed density and velocity are given by 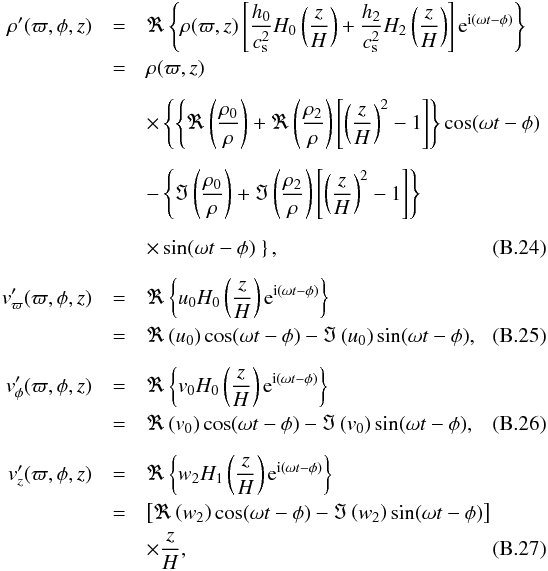 where the unperturbed density ρ(ϖ,z) is given by Eq. (A.4) and the density perturbation is related to the enthalpy perturbation by
where the unperturbed density ρ(ϖ,z) is given by Eq. (A.4) and the density perturbation is related to the enthalpy perturbation by ![]() and
and ![]() .
.
Equations (B.24) to (B.27) provide the 3D density and kinematic structure of the perturbed disk. In the framework of
the 2.5D formalism, the second-order terms, namely w2 and ρ2, are taken as equal to zero. Consequently, the z component of the velocity field (![]() ) and the z-dependent terms of the perturbed density (ρ′) are neglected. The final solution is thus independent of the vertical coordinate and includes zeroth-order terms only.
) and the z-dependent terms of the perturbed density (ρ′) are neglected. The final solution is thus independent of the vertical coordinate and includes zeroth-order terms only.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


