| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322695 | |
| Published online | 09 March 2015 | |
Online material
Appendix A: Auxiliary tables
Tables A.1−A.3 contain the probabilities for X atom desorption, OX desorption, and X2O and HDO desorption (X = H, D), respectively, at Tice = 20, 30, and 60 K.
X atom photodesorption probabilities at Tice = 20 K, 30 K, and 60 K resulting from photoexcitation of a X2O (X = H, D) or XOY (HOD or DOH) molecule present in a specific monolayer of H2O ice.
OX radical photodesorption probabilities at Tice = 20 K, 30 K, and 60 K resulting from photoexcitation of a X2O (X = H, D) or XOY (HOD or DOH) molecule present in a specific monolayer of H2O ice.
Total X2O (X = H, D) or XOY (HOD or DOH) photodesorption probabilities at Tice = 20 K, 30 K, and 60 K per monolayer due to the direct and the kick-out mechanism for X2O and XOY photodissociation in H2O ice.
Appendix B: Fitting formulae for photodesorption probabilities
Tables 2, 4, 5, A.1−A.3 list the total probabilities for X desorption, OX desorption, and X2O and HDO desorption (X = H, D) following a dissociation event, as a function of both monolayer and ice temperature. These tables also give the average probabilities, over the top four monolayers, for each species. For use in astrochemical models, it is useful to know the probability (per monolayer) of every potential outcome, rather than the total probability for the desorption of each species. This is because, in full gas-grain models, one is also interested in the composition of the ice mantle, as well as the gas.
As discussed in the main body of this paper, there are six potential outcomes following a dissociation event which can lead to a change in composition of both the ice and gas. For example, for HDO which is dissociated into H + OD,  Equation (B.6) is the process known as “kick out” whereby a neighbouring H2O is ejected from the ice via momentum transfer from an excited photofragment. The probabilities of each of these events as a function of monolayer and ice temperature have been compiled from the raw data of the molecular dynamics simulations and are available at the CDS. There is a seventh possibility in which the photofragments recombine to reform HDO which remains trapped in the ice. This process does not change the gas or ice composition and thus we have not listed the probabilities for this outcome here; however, these data are necessary if one is interested in extrapolating the probabilities to deeper monolayers, ML > 4.
Equation (B.6) is the process known as “kick out” whereby a neighbouring H2O is ejected from the ice via momentum transfer from an excited photofragment. The probabilities of each of these events as a function of monolayer and ice temperature have been compiled from the raw data of the molecular dynamics simulations and are available at the CDS. There is a seventh possibility in which the photofragments recombine to reform HDO which remains trapped in the ice. This process does not change the gas or ice composition and thus we have not listed the probabilities for this outcome here; however, these data are necessary if one is interested in extrapolating the probabilities to deeper monolayers, ML > 4.
To determine the desorption probabilities at temperatures and in monolayers outside of those tabulated, one can simply interpolate/extrapolate using, for example, cubic spline interpolation. However, when extrapolating to determine probabilities for deeper monolayers, ML > 4, one should take care to ensure that, deep into the ice mantle, the probabilities for outcomes (B.1), (B.2), (B.3), (B.5), and (B.6) tend to 0, and the probability for outcome (B.4) tends to 1 − Precom, where Precom is the probability that the photofragments recombine to reform the molecule (which remains trapped in the ice). Deeper into the ice, desorption events become increasingly less probable and the most probable outcome becomes trapping of the photofragments (or the reformed molecule, following recombination). In addition, at very low coverage, ML < 1, the rates for all outcomes should tend to 0 as ML → 0.
In Table 1 we present our fitting functions and corresponding best-fit parameters for the temperature-averaged probabilities per monolayer for each outcome. The probabities are well fitted using a Gaussian-like function with the exception of the outcomes leading to trapping of the OY radical for which an exponential-like function was found to be more appropriate for describing the asymptotic behaviour of the probabilities towards deeper monolayers (≫4). In Fig. B.1 we present the probability per monolayer at each temperature and the temperature-averaged probabilities per monolayer along with the fitted functions for the example of DOH∗. The probabilities were fitted using the non-linear least-squares (NLLS) Marquardt-Levenberg algorithm (Marquardt 1963). The probabilities are a much stronger function of monolayer than temperature; hence, our decision to fit functions with respect to monolayer only.
For implementation in chemical models which adopt the rate equation method for describing the ice chemistry and gas-grain balance, the probabilities per monolayer should be multiplied by the rate of arrival of UV photons in the wavelength range 1650−1300 Å onto the grain surface times the absorption cross section of a UV photon by a grain-surface site (or molecule, in this case, HDO). The total desorption rate is then determined by integrating the desorption rate per monolayer over the total number of monolayers on the grain. The probabilities can be directly employed in stochastic chemical models in which the discrete nature of chemical reactions are taken into account (see, e.g. Cuppen & Herbst 2007).
 |
Fig. B.1
Temperature-specific probabilities, temperature-averaged probabilities, and fitted functions for each outcome as a function monolayer for HDO photodissociation into D + OH. |
| Open with DEXTER | |
Appendix C: Photodesorption and fractionation
This section investigates whether photodesorption ultimately also leads to fractionation of HDO/H2O in the gas. We can estimate the total photodesorption probability ratio between HDO and H2O by taking into account the direct and kicked out mechanism in both cases. The probability of HDO photodesorption through the direct mechanism is given by ![]() (C.1)In Eq. (C.1), Pdirect( HDO∗) is the probability that upon photo-excitation of HDO (the generic case) the HDO recombines and desorbs directly. It can be approximately calculated using
(C.1)In Eq. (C.1), Pdirect( HDO∗) is the probability that upon photo-excitation of HDO (the generic case) the HDO recombines and desorbs directly. It can be approximately calculated using ![]() (C.2)and rHDO is the original HDO/H2O ratio in the ice (of the order of 0.01 or less as indicated by observations). In Eq. (C.2), the probabilities on the right hand side are the probabilities for the direct mechanism for photodesorbing HDO averaged over the top four monolayers and presented in Tables 5 and A.3.
(C.2)and rHDO is the original HDO/H2O ratio in the ice (of the order of 0.01 or less as indicated by observations). In Eq. (C.2), the probabilities on the right hand side are the probabilities for the direct mechanism for photodesorbing HDO averaged over the top four monolayers and presented in Tables 5 and A.3.
The probability of H2O photodesorption through the direct mechanism is given by ![]() (C.3)In Eq. (C.3), Pdirect(H2O∗) is the probability that upon photo-excitation H2O recombines and desorbs directly. It can be obtained directly from Tables 5 and A.3.
(C.3)In Eq. (C.3), Pdirect(H2O∗) is the probability that upon photo-excitation H2O recombines and desorbs directly. It can be obtained directly from Tables 5 and A.3.
As can be seen from Table 2 and after using Eq. (C.2), Pdirect(HDO∗) and Pdirect(H2O∗) are roughly the same. As a result ![]() (C.4)meaning that there is no isotope fractionation due to the direct mechanism.
(C.4)meaning that there is no isotope fractionation due to the direct mechanism.
Now consider the kick-out mechanism. The indirect probabilities can be written as follows: 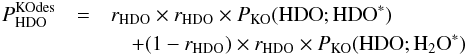 (C.5)and
(C.5)and 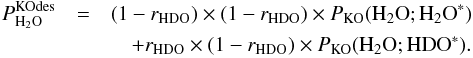 (C.6)In Eqs. (C.5) and (C.6),
(C.6)In Eqs. (C.5) and (C.6), ![]() is the probability of desorption of HXO through the kick-out mechanism, where X is either H or D. Furthermore, PKO(HX1O; HX2O∗) is the probability that HX1O is kicked out after photo-excitation of HX2O, where X1 can either be H or D, and X2 can also be H or D. As for the direct mechanism, we can approximately calculate PKO(HX1O;HX2O∗) from
is the probability of desorption of HXO through the kick-out mechanism, where X is either H or D. Furthermore, PKO(HX1O; HX2O∗) is the probability that HX1O is kicked out after photo-excitation of HX2O, where X1 can either be H or D, and X2 can also be H or D. As for the direct mechanism, we can approximately calculate PKO(HX1O;HX2O∗) from 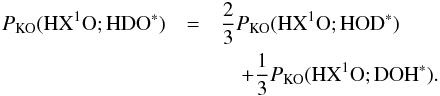 (C.7)The two quantities on the right hand side of Eq. (C.7) have been tabulated for X1 equal to H in Tables 5 and A.3.
(C.7)The two quantities on the right hand side of Eq. (C.7) have been tabulated for X1 equal to H in Tables 5 and A.3.
Because we have only calculated probabilities that H2O is kicked out, we make the following approximations, 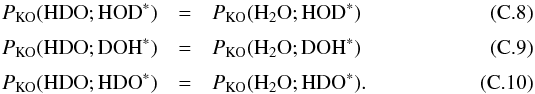 The right hand values of Eqs. (C.8) and (C.9) can be directly obtained from Tables 5 and A.3. PKO( HDO; HDO∗) can be computed using the approximation in Eq. (C.10) and using Eq. (C.7) and Tables 5 and A.3.
The right hand values of Eqs. (C.8) and (C.9) can be directly obtained from Tables 5 and A.3. PKO( HDO; HDO∗) can be computed using the approximation in Eq. (C.10) and using Eq. (C.7) and Tables 5 and A.3.
Using Eqs. (C.8)–(C.10), Eq. (C.5) can be rewritten as 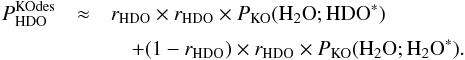 (C.11)Most importantly, for 10 and 20 K we have approximately that (see Tables 5 and A.3)
(C.11)Most importantly, for 10 and 20 K we have approximately that (see Tables 5 and A.3) ![]() (C.12)
(C.12)
Inserting Eq. (C.12) in Eq. (C.11) yields ![]() (C.13)and inserting Eq. (C.12) in Eq. (C.6) yields
(C.13)and inserting Eq. (C.12) in Eq. (C.6) yields ![]() (C.14)From Eqs. (C.13) and (C.14), we can derive that
(C.14)From Eqs. (C.13) and (C.14), we can derive that ![]() (C.15)meaning that there should be no isotope fractionation due to the indirect kick-out mechanism. Taken together, Eqs. (C.4) and (C.15) ensure that the ratio of desorbed HDO over desorbed H2O in the ice is given by
(C.15)meaning that there should be no isotope fractionation due to the indirect kick-out mechanism. Taken together, Eqs. (C.4) and (C.15) ensure that the ratio of desorbed HDO over desorbed H2O in the ice is given by ![]() (C.16)which means that this ratio is simply equal to the ratio of HDO and H2O in the ice. Therefore, isotope fractionation does not occur for HDO and H2O photodesorption.
(C.16)which means that this ratio is simply equal to the ratio of HDO and H2O in the ice. Therefore, isotope fractionation does not occur for HDO and H2O photodesorption.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


