| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 30 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424081 | |
| Published online | 20 November 2014 | |
Online material
3.6 μm coreshine intensity and 4.5/3.6 coreshine ratio sorted by increasing ratio value for each detected cloud of the four regions.
Appendix A: Isotropy versus anisotropy for the incident radiation field
 |
Fig. A.1
A cubic cloud filled with scattering (absorptionless) dust at constant density in an isotropic (upper row) or isotropic+anisotropic field (lower row). The left column shows only the scattered photons, the middle column the opacity along the line of sight (identical for both cases), and the right column the net surface brightness. |
| Open with DEXTER | |
Coreshine (and any types of scattering processes) can only be seen in emission if it follows a number of conditions, as discussed in Sect. 4.2. Another compulsory condition is the anisotropy of the incident ISRF. This anisotropy can come from large scales (such as the Galactic structure) or small scales (such as stars, near or far). To illustrate the importance of anisotropy we considered two simple cases: only isotropic illumination, or the combination of one type of anisotropic source with the isotropic illumination.
If the ISRF is isotropic, there is no preferred direction for photons to travel. To see the cloud in emission, we need to introduce some anisotropy to concentrate photons toward a privileged direction, that is, toward the observer. The cloud would therefore have to produce this anisotropy. To increase the number of photons toward the observer, the cloud would have to act like a telescope mirror pointed at Earth to collect photons from many directions to redirect them in a single direction (this would of course lower the number of photons scattered in some other directions). Since the cloud has no such focusing capabilities and the observer no privileged position, an isotropic ISRF cannot make a cloud glow. In fact, for any direction across the cloud there are as many deviated photons away from that line than there are photons from other directions that are deviated into that propagation line and all the scatterings cancel out. This is in an ideal case without absorption. In presence of absorption, a part of the photons are lost and the cloud can only appear as a darker object against the background sky, never in emission. The field must therefore be anisotropic.
In the anisotropic case, there is one noticeable direction, which is the line going from the localized light source to the cloud (we consider a single source of photons, such as a nearby star, superimposed on an isotropic ISRF). This is the path with the highest number of photons traveling toward the cloud. As in the isotropic case, photons enter from all directions and are partly deviated, partly untouched (and partly absorbed, but we still ignore absorption here). The difference to the isotropic case is that across the cloud along this particular line, there will be
more deflected photons away from it than photons brought back onto it. The opposite can occur for some or all of the other directions (depending on details such as the phase function of the grain-scattering properties). Therefore, away from this path, the number of deviated photons that leave the cloud increases (while it decreases along the path). Eventually, there can be more photons deviated toward the observer from the anisotropic source than photons coming from behind the cloud and deviated away from the observer. The net effect is to show the cloud in emission.
To illustrate this effect we ran a model based on a cube of constant density, tilted at 30° angles on two axes to see the edges and three sides. The cube is either in an isotropic field or a composite of isotropic and anisotropic fields. It is filled with dust with only scattering capability (absorption coefficient is set to zero). Figure A.1 shows the results. The left column shows slightly different images of scattered photons, but taking into account the background illumination absorption due to the cloud opacity (displayed in the central figure), following Eq. (3), the cloud completely disappears in the isotropic field. This is explained by the fact that all the photons scattered toward the observer (as seen in the left panel) are exactly compensated for by the photons scattered away from the line of sight for the radiation field coming from behind the cloud. A close inspection of the image reveals the cube only by the numerical noise of the Monte Carlo radiative transfer code . If the cloud opacity had not been set to zero, the cloud would have been seen in absorption against the background, while for the isotropic+anisotropic case, the cloud would have appeared in emission or in absorption, depending on the balance (Sect. 4.2).
Appendix B: Global method for subtracting the stellar contribution
We assume that the intensity in the DIRBE1 (1.25 μm) and DIRBE2 (2.2 μm) bands is only due to the sum of individual stellar contributions (PSC): 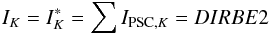 (B.1)\newpage
(B.1)\newpage (B.2)
(B.2)
The intrinsic color Iint of the stellar component was measured from high Galactic latitude and low dust emission regions and is also equal to 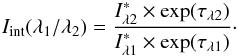 (B.3)
(B.3)
We deduce the extinction on each line of sight by using the measured value of the intrinsic color between J and K (Iint(J/K) = 1.), its definition (Eq. (B.3)) and the previous assumptions (Eqs. (B.1) and (B.2)), 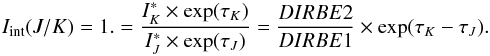 (B.4)
(B.4)
Finally, we use Eq. (B.3) to yield the stellar contribution in each band, 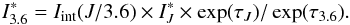 (B.5)
(B.5)
Taking into account our assumption (Eq. (B.2)) and the conversion coefficient deduced from the extinction curve of Rieke & Lebofsky (1985) with RV = 3.1, we obtain 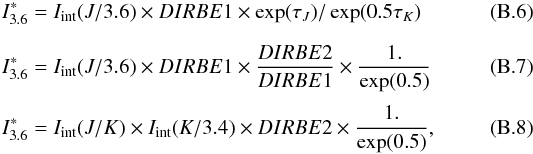 with Iint(J/K) = 1. and Iint(3.4 /K) = 1.7 (Bernard et al. 1994).
with Iint(J/K) = 1. and Iint(3.4 /K) = 1.7 (Bernard et al. 1994).
We obtain the diffuse emission map, 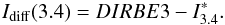 (B.9)
(B.9)
In the same way, using Iint(4.9 / 3.4) = 2.1, we compute the other diffuse emission map, 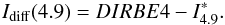 (B.10)
(B.10)
Appendix C: Source sample
Source table classified region by region.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


