| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 31 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201323021 | |
| Published online | 01 December 2014 | |
Online material
Appendix A: The minimum mass solar nebula scaling
We provide in Table A.1 the main quantities that are used in the article and present their scaling in the so-called minimum mass solar nebula formalism (Hayashi 1981; Nakagawa et al. 1986).
Expressions for the minimum mass nebula scaling used in this article.
Appendix B: Geometric collision probability with shear
We derive the expression for the geometric collision probability and show that it is identical to that derived by Ormel & Klahr (2010). From Eqs. (23a) and (23b) and accounting for both the (assumed inward) radial velocity of the gas due turbulent viscosity vν and the shear in the disk, 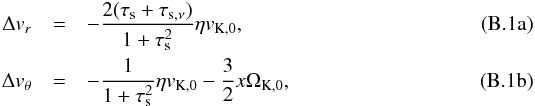 where, following Ormel & Klahr (2010), we have used an expansion around the location of the planetesimal (ΩK,0 ≡ ΩK(x = 0)), and x is the radial distance from the planetesimal at which the collision with the dust particle takes place. For simplicity, we assume that on average x = Rp/ 2. This yields the impact rate in the geometrical limit as:
where, following Ormel & Klahr (2010), we have used an expansion around the location of the planetesimal (ΩK,0 ≡ ΩK(x = 0)), and x is the radial distance from the planetesimal at which the collision with the dust particle takes place. For simplicity, we assume that on average x = Rp/ 2. This yields the impact rate in the geometrical limit as: 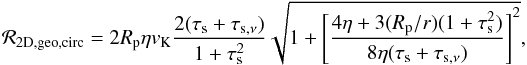 (B.2)where we have dropped the 0 labels. When vν = 0, this expression is equivalent to Eq. (22) of Ormel & Klahr (2010) who derive this impact rate by an analysis of the trajectory of dust particles. In most cases, we will consider ητs ≪ Rp/r so that shear may be neglected and
(B.2)where we have dropped the 0 labels. When vν = 0, this expression is equivalent to Eq. (22) of Ormel & Klahr (2010) who derive this impact rate by an analysis of the trajectory of dust particles. In most cases, we will consider ητs ≪ Rp/r so that shear may be neglected and ![]() : the collision rate is the product of the cross section 2Rp and the encounter velocity
: the collision rate is the product of the cross section 2Rp and the encounter velocity ![]() .
.
The 2D probability that a planetesimal will accrete a given dust grain is then given by Eq. (35): 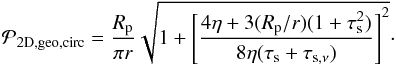 (B.3)This equation may be approximated in the different regimes (from small to large particles):
(B.3)This equation may be approximated in the different regimes (from small to large particles): 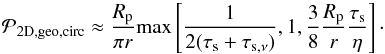 (B.4)The lowest capture probability Rp/πr corresponds to dust particles with τs ~ 1 which drift in with a speed that is comparable to the headwind felt by the planetesimal. One can expect that these particles will be the most difficult to filter. For smaller τs values, the slower drift leads to a higher probability, limited by the gas drift. For large τs values, the drift rate also decreases and the effect of the Keplerian shear across the planetesimal becomes dominant. The capture probability then becomes a very steep function of the planetesimal size (∝
(B.4)The lowest capture probability Rp/πr corresponds to dust particles with τs ~ 1 which drift in with a speed that is comparable to the headwind felt by the planetesimal. One can expect that these particles will be the most difficult to filter. For smaller τs values, the slower drift leads to a higher probability, limited by the gas drift. For large τs values, the drift rate also decreases and the effect of the Keplerian shear across the planetesimal becomes dominant. The capture probability then becomes a very steep function of the planetesimal size (∝![]() in the Epstein regime and ∝
in the Epstein regime and ∝![]() in the Stokes regime). However, shear becomes important only for very large planetesimals (
in the Stokes regime). However, shear becomes important only for very large planetesimals (![]() for the MMSN). It only concerns cases for which the collisions take place in the settling or three-body regimes. Shear can thus be neglected for the geometrical regime.
for the MMSN). It only concerns cases for which the collisions take place in the settling or three-body regimes. Shear can thus be neglected for the geometrical regime.
Appendix C: Analytical estimates for small grains (geometric, hydro, and settling regimes)
We provide here analytical estimates for the collision probabilities and filtering efficiencies for the geometric and settling regimes. In order to provide tractable relations, we make the following simplifications:
-
We study only small particles such that τs< 1, corresponding generally to s~<1 m.
-
Given the above assumption, we use Δv = ηvK for the dust-planetesimal encounter velocity.
-
We approximate χα,τs defined by Eq. (46)as follows:
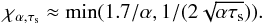 (C.1)We thus separate small particles with τs ≤ τs,ν ~ 0.32α which have not settled from larger particles for which hd(τs) <hg.
(C.1)We thus separate small particles with τs ≤ τs,ν ~ 0.32α which have not settled from larger particles for which hd(τs) <hg. -
We consider cases for which the planetesimal capture radius is smaller than the dust disk scale height and thus Eq. (43)can be simplified as:
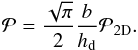 (C.2)
(C.2) -
We do not consider the Safronov and three-body regimes.
|
Fig. C.1
Value of the effective capture radius bset in units of the Bondi radius rB from Eq. (90)(colored curves) together with the approximation used in Eq. (C.3)(thick black lines). Left panel: solution when the Bondi radius is smaller than the Hill radius. Right panel: solution when the Bondi radius is larger than the Hill radius (specifically, the solution of Eq. (90)is shown for RB/RH = 10). |
|
| Open with DEXTER | |
Given a known encounter velocity, the calculation of the collision probability only requires that of the planetesimal effective capture radius. We know that it is extremely small in the hydro regime and equal to Rp in the geometric regime. In the settling regime, it is given by Eq. (90). As shown in Fig. 9, the settling regime may be subdivided into a Bondi regime in which the capture radius is proportional to ![]() , and a Hill regime in which the capture radius is approximatively independent of τs and equal to the Hill radius. We thus approximate the effective capture radius of planetesimals/embryos in the different regimes as
, and a Hill regime in which the capture radius is approximatively independent of τs and equal to the Hill radius. We thus approximate the effective capture radius of planetesimals/embryos in the different regimes as  (C.3)and
(C.3)and ![]() is defined by Eq. (88). The different regimes are defined by the following relations:
is defined by Eq. (88). The different regimes are defined by the following relations: 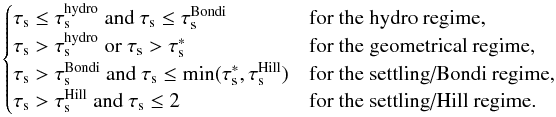 (C.4)The dimensionless stopping times for the different regimes are defined by Eq. (88)for
(C.4)The dimensionless stopping times for the different regimes are defined by Eq. (88)for ![]() , Eq. (100)and τf = 1 for
, Eq. (100)and τf = 1 for ![]() ,
, ![]() for
for ![]() , and
, and ![]() for τHill. These and their MMSN approximations are thus respectively:
for τHill. These and their MMSN approximations are thus respectively:
 It can be seen that the value of
It can be seen that the value of ![]() is proportional to μp and reaches
is proportional to μp and reaches ![]() for the Hill-dominated settling regime (Rp ~ 1000 km). Importantly,
for the Hill-dominated settling regime (Rp ~ 1000 km). Importantly, ![]() for
for ![]() , with
, with 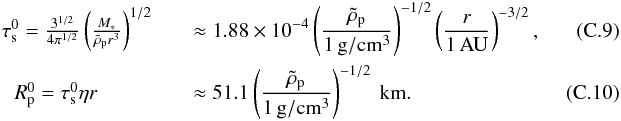
Appendix C.1: Collision probabilities
Using Eqs. (C.2), (31), (35), (80), (81), and (88), the collision probabilities for the three regimes defined in Eq. (C.3)can be written  (C.11)When using the approximation from Eq. (C.1)and the MMSN scalings from Appendix A, this yields for small particles such that τs< 0.09α:
(C.11)When using the approximation from Eq. (C.1)and the MMSN scalings from Appendix A, this yields for small particles such that τs< 0.09α:  (C.12)and for medium-sized particles such that
(C.12)and for medium-sized particles such that ![]() :
:  (C.13)We note that in these expressions, the scaling of the particle size (stopping time) was adjusted to be centered on the maximum collision probability in each regime.
(C.13)We note that in these expressions, the scaling of the particle size (stopping time) was adjusted to be centered on the maximum collision probability in each regime.
|
Fig. C.2
Value of the collision probability |
|
| Open with DEXTER | |
Figure C.2 shows that the simplified solutions are good approximations of the full solutions, except for large grains with τs~>2 and at the interface between the settling and geometric regimes (along the ![]() line). In the settling regime, the maximum collision probability is obtained for dust such that
line). In the settling regime, the maximum collision probability is obtained for dust such that ![]() , i.e., with a stopping time equal to the Hill sphere crossing time. For a low value of the turbulence parameter α = 10-4, a 1 M⊕ embryo (corresponding to Rp = 11250 km for a
, i.e., with a stopping time equal to the Hill sphere crossing time. For a low value of the turbulence parameter α = 10-4, a 1 M⊕ embryo (corresponding to Rp = 11250 km for a ![]() density) would have
density) would have ![]() /
/![]() for particles such that
for particles such that ![]() , i.e., for centimeter-sized pebbles between 1 AU and 10 AU.
, i.e., for centimeter-sized pebbles between 1 AU and 10 AU.
Appendix C.2: Filtering efficiency
The filtering efficiency as defined by Eq. (58)writes for the regimes considered: 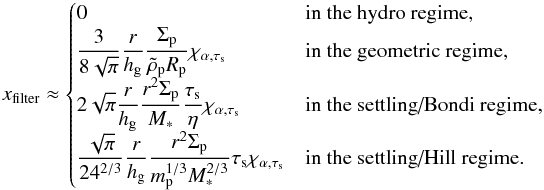 (C.14)The MMSN scaling then yields, for small particles such that τs< 0.09α:
(C.14)The MMSN scaling then yields, for small particles such that τs< 0.09α:  (C.15)and for medium-sized particles such that
(C.15)and for medium-sized particles such that ![]() :
: 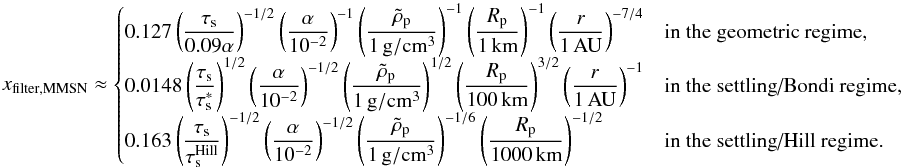 (C.16)
(C.16)
|
Fig. C.3
Value of the filtering efficiency log xfilter obtained by the full theory (black contours) and by the simplified one (red contours), for the MMSN and α = 10-4. The two panels are for two orbital distances: 0.1 AU (left) and 5 AU (right). (See Fig. C.2 for a full description.) |
|
| Open with DEXTER | |
Figure C.3 compares the values of xfilter obtained with the full theory and the simplified one, again showing good agreement except for large grains beyond meter size and near the ![]() line. For increasing planetesimal sizes, the maximum filtering efficiency is obtained along
line. For increasing planetesimal sizes, the maximum filtering efficiency is obtained along ![]() , then
, then ![]() and finally
and finally ![]() .
.
Appendix D: Results for a disk with α = 10-4
Given the inefficient filtering obtained in the high turbulence (α = 10-2) case, we now consider the weak turbulence case (α = 10-4). This is more favorable because dust settles closer to the mid-plane and the mean gas flow is also slower.
Figures D.1 and D.2 show the resulting filtering efficiency, both at 1 AU and for 1 mm dust, as a function of orbital distance. At 1 AU, efficient filtering is achieved for a wider range of dust and planetesimal sizes, basically for dust of 10 μm to 1 cm and planetesimals of less than a few kilometers in radius. A small island with xfilter~>1 also appears in the settling regime, for meter-sized dust and planetesimals of ~1000 km in radius. Compared to Figs. 18 and 19 in the α = 10-2 case, there is about an order of magnitude increase in the filtering efficiency.
 |
Fig. D.1
Contours of the filtering efficiency by a MMSN planetesimal disk at 1 AU for α = 10-4, assuming monodisperse size distributions for planetesimals and dust grains. The contour indicating perfect filtering efficiency for log 10xfilter = 0 is shown in bold. |
| Open with DEXTER | |
 |
Fig. D.2
Contours of the filtering efficiency by a MMSN planetesimal disk for 1 mm dust for α = 10-4, assuming a monodisperse size distribution for planetesimals. The contour indicating perfect filtering efficiency for log 10xfilter = 0 is shown in bold. |
| Open with DEXTER | |
Figure D.3, shows how a lower value of the turbulence parameter α = 10-4 affects filtering by a distribution of planetesimals between 1 km and 1000 km. Compared to Fig. 20 for α = 10-2, filtering is found to be more efficient of course. For example, dust of 1 mm in size can now be efficiently captured in an MMSN disk inside about 0.03 AU while a value of xfilter = 1 is never reached for the high turbulence case until the gas disk has shrunk to about 1% of the MMSN value. Similarly, 1 cm grains can be captured with an efficiency close to unity inside of 0.1 AU compared to about 0.05 AU for the α = 10-2 case. In the 0.1−1 AU range, a wide range of small grains may be captured with an efficiency between 1 and 0.1. The dependence as a function of ![]() remains relatively weak, as in the strong turbulence case.
remains relatively weak, as in the strong turbulence case.
 |
Fig. D.3
Filtering efficiency of a swarm of planetesimals with radii between 1 km and 1000 km as a function of orbital distance and mass of the gas disk for α = 10-4. (See Fig. 20 for details.) |
| Open with DEXTER | |
Appendix E: Dependence on the planetesimal scale height
All the results presented so far have assumed a rather low value of the planetesimal scale height hp = 0.01hg. This favors the filtering of particles able to settle to the mid-plane in a thin plane. In Fig. E.1 we show how the integrated filtering efficiency Xfilter depends on the value of hp. We select a low value of the turbulence parameter α = 10-4 because this is where the differences are most important. With an infinitely thin planetesimal disk (hp = 0, left panels), we obtain results that are very similar to our fiducial case (hp/hg = 0.01) shown in Fig. 22.
 |
Fig. E.1
Filtering efficiency of dust from 1 micron to 100 meters by a MMSN planetesimal belt with planetesimals of 1 − 10,000 km in radius extending from 0.1 to 35 AU for a turbulent parameter α = 10-4 and various ratios of the planetesimal to gas scale height, from an infinitely thin planetesimal disk with hp/hg = 0 (left panels), hp/hg = 0.1 (middle panels), and hp/hg = 1.0 (right panels). As in Figs. 21 and 22, the top panels show the contours of the disk-integrated filtering factor Xfilter while the bottom panels show the orbital distance at which Xfilter(r) = 1 for dust particles drifting in from beyond 35 AU. |
| Open with DEXTER | |
When we increase the planetesimal scale height, the filtering of large particles becomes less efficient, as shown by the middle and right panels of Fig. E.1. Specifically, compared to the case when hp = 0, changes occur for particles larger than about 1 cm when we consider hp/hg = 0.1 and for particles larger than about 0.1 cm when we consider hp/hg = 1.0.
We first consider the limit for which Eq. (43)becomes independent of hp and the problem may be considered 2D. This occurs when the cross section of the embryos becomes so large that b> (2/![]() . By writing β ≡ RH/b, one may show that this occurs when
. By writing β ≡ RH/b, one may show that this occurs when 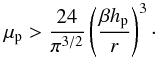 (E.1)For the MMSN disk at 1 AU, this is equivalent to
(E.1)For the MMSN disk at 1 AU, this is equivalent to ![]()
![]() For large embryos we expect β~>1 with a significant dependence on τs (see Appendix C). In the regime that we considered in this work Eq. (E.1)is not satisfied, but it would be for embryos larger than a few Earth masses which may then accrete more efficiently.
For large embryos we expect β~>1 with a significant dependence on τs (see Appendix C). In the regime that we considered in this work Eq. (E.1)is not satisfied, but it would be for embryos larger than a few Earth masses which may then accrete more efficiently.
The decrease of the filtering efficiency with increasing hp value seen in Fig. E.1 is hence a direct consequence of the fact that when Eq. (E.1)is not satisfied, the 3D collision probability given by Eq. (43)depends on the maximum of hd and hp. The probability thus becomes dependent on hp when hp>hd, that is when ![]() (E.2)For α = 10-4, this implies that we expect lower collision probability and filtering efficiency when compared to the hp = 0 case when τs = 10-2 for hp/hg = 0.1 and τs = 10-4 for hp/hg = 1. According to Fig. 3 (around 1 AU), this corresponds to s ≈ 1 cm and 1 mm, in good agreement with the results of Fig. E.1.
(E.2)For α = 10-4, this implies that we expect lower collision probability and filtering efficiency when compared to the hp = 0 case when τs = 10-2 for hp/hg = 0.1 and τs = 10-4 for hp/hg = 1. According to Fig. 3 (around 1 AU), this corresponds to s ≈ 1 cm and 1 mm, in good agreement with the results of Fig. E.1.
The question whether large boulders may be efficiently filtered by planetary embryos thus depends crucially on whether these embryos effectively lie close to the mid-plane. In the case of a weakly turbulent disk with α = 10-4, this is the case when the ratio of the embryo to gas scale height hp/hg = 0.01 or lower, but we notice that an efficient filtering in the settling regime becomes limited to pebbles less than about a meter in size when hp/hg = 0.1 and that it mostly disappears for hp = hg. A detailed, size-dependent calculation of hp is therefore critical to determine whether planetary embryos may filter large particles in the disk and grow through that mechanism.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


