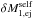| Issue |
A&A
Volume 570, October 2014
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201423730 | |
| Published online | 09 October 2014 | |
Online material
Appendix A: The perturbing forces 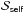 and
and 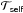
Consider a primary star of mass M1. At time t = t0, it has an orbital velocity v1 = v0, and an orbital angular velocity ω. At a later time t = t′, a particle is ejected from the primary at the inner-Lagrangian point, located at a distance rℒ1 from the primary’s mass centre (see Fig. A.1), and so the primary’s mass becomes 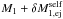 , where
, where 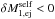 . The particle’s absolute velocity is
. The particle’s absolute velocity is 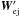 . As a result, the centre of mass is shifted by
. As a result, the centre of mass is shifted by 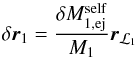 (A.1)with respect to its unperturbed location, and its new orbital velocity is
(A.1)with respect to its unperturbed location, and its new orbital velocity is 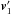 . During a time interval δt, the change in the primary’s orbital velocity is (see Hadjidemetriou 1969b; Sepinsky et al. 2007b, for further details)
. During a time interval δt, the change in the primary’s orbital velocity is (see Hadjidemetriou 1969b; Sepinsky et al. 2007b, for further details) 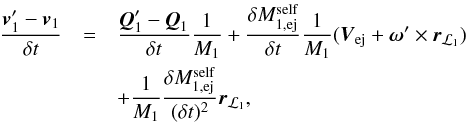 (A.2)where Q1 is the primary’s momentum, primed quantities indicate values at time t′, and Vej = Wej − v1 is the relative velocity of the ejected material with respect to the primary’s mass centre.
(A.2)where Q1 is the primary’s momentum, primed quantities indicate values at time t′, and Vej = Wej − v1 is the relative velocity of the ejected material with respect to the primary’s mass centre.
At self-accretion, the primary accretes the particle of mass 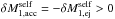 . Just before self-accretion occurs at time t = t′′, the momentum of the primary and ejected particle,
. Just before self-accretion occurs at time t = t′′, the momentum of the primary and ejected particle, 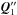 , is
, is 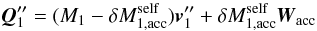 (A.3)where Wacc is the absolute velocity of the self-accreted particle. The orbital velocity,
(A.3)where Wacc is the absolute velocity of the self-accreted particle. The orbital velocity, 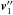 , is the sum of the non-perturbed orbital velocity at time t′′,
, is the sum of the non-perturbed orbital velocity at time t′′, 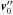 , and the perturbation to the velocity because of the original ejection episode, so
, and the perturbation to the velocity because of the original ejection episode, so 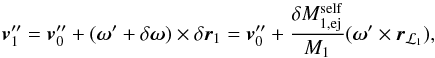 (A.4)
(A.4)
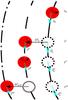 |
Fig. A.1
Illustration of the self-accretion process. At time t = t0, the donor star moves along its orbital path (solid black curve), with an orbital velocity v0 (cyan arrow). At t′, a particle of mass |
| Open with DEXTER | |
where we have used Eq. (A.1) and ignored terms larger than first-order. Inserting Eq. (A.4) into Eq. (A.3) gives 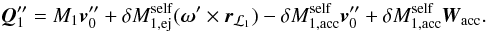 (A.5)The particle is self-accreted at time t′′′, at a location
(A.5)The particle is self-accreted at time t′′′, at a location 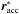 with respect to the primary’s mass centre. This shifts the mass centre by an amount
with respect to the primary’s mass centre. This shifts the mass centre by an amount 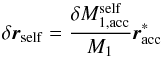 (A.6)and the primary’s momentum is now
(A.6)and the primary’s momentum is now 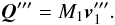 (A.7)The new orbital velocity,
(A.7)The new orbital velocity, 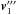 , is the sum of the unperturbed orbital velocity,
, is the sum of the unperturbed orbital velocity, 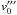 , and the perturbations to the velocity arising from the ejection and self-accretion processes, i.e.
, and the perturbations to the velocity arising from the ejection and self-accretion processes, i.e. 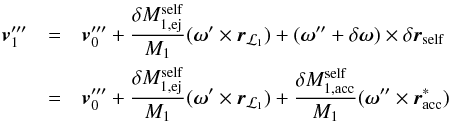 (A.8)where we have used Eq. (A.6), and once again ignored terms higher than first-order. Inserting Eq. (A.8) into Eq. (A.7) yields
(A.8)where we have used Eq. (A.6), and once again ignored terms higher than first-order. Inserting Eq. (A.8) into Eq. (A.7) yields 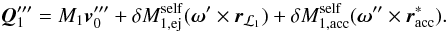 (A.9)Taking the difference between Eqs. (A.9) and (A.5), dividing the result by δt and using the fact that
(A.9)Taking the difference between Eqs. (A.9) and (A.5), dividing the result by δt and using the fact that 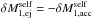 yields
yields 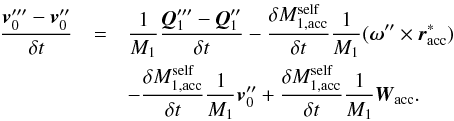 (A.10)Following Sepinsky et al. (2007b), the absolute acceleration of the primary’s mass centre is the sum of Eq. (A.10), the relative acceleration of the primary’s mass centre,
(A.10)Following Sepinsky et al. (2007b), the absolute acceleration of the primary’s mass centre is the sum of Eq. (A.10), the relative acceleration of the primary’s mass centre, 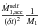 , and the Coriolis acceleration,
, and the Coriolis acceleration, 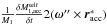 to give
to give 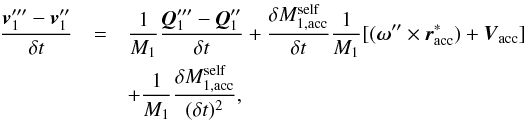 (A.11)where
(A.11)where  is the relative velocity of the self-accreted particle with respect to the primary’s mass centre.
is the relative velocity of the self-accreted particle with respect to the primary’s mass centre.
Summing Eqs. (A.11) and (A.2) gives the acceleration of the primary’s mass centre from both the ejection and self-accretion process. In the limit δt → 0, and remembering that 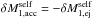 , then the acceleration of the primary’s mass centre is
, then the acceleration of the primary’s mass centre is 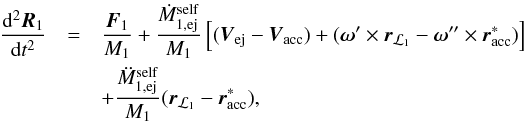 (A.12)where R1 is the position vector of the primary with respect to an inertial reference frame, and F1 is the sum of all external forces acting on the primary, which writes as
(A.12)where R1 is the position vector of the primary with respect to an inertial reference frame, and F1 is the sum of all external forces acting on the primary, which writes as 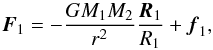 (A.13)where r = R2 − R1, R2 is the position vector of the secondary, and f1 is the force acting on the primary via the matter stream. Since the secondary is not accreting, its equation of motion is
(A.13)where r = R2 − R1, R2 is the position vector of the secondary, and f1 is the force acting on the primary via the matter stream. Since the secondary is not accreting, its equation of motion is 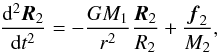 (A.14)where f2 is the force acting on the secondary by the accretion stream. Subtracting Eq. (A.12) from Eq. (A.14) gives the equation of motion of the secondary with respect to the primary, which is
(A.14)where f2 is the force acting on the secondary by the accretion stream. Subtracting Eq. (A.12) from Eq. (A.14) gives the equation of motion of the secondary with respect to the primary, which is 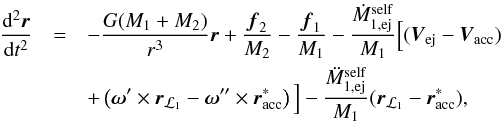 (A.15)which takes the form
(A.15)which takes the form 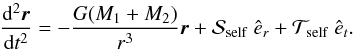 (A.16)Here, êr is a unit vector pointing along r, and êt is a unit vector perpendicular to êr in the direction of the orbital motion. Taking the dot product of Eq. (A.16) with êr and êt respectively, yields
(A.16)Here, êr is a unit vector pointing along r, and êt is a unit vector perpendicular to êr in the direction of the orbital motion. Taking the dot product of Eq. (A.16) with êr and êt respectively, yields 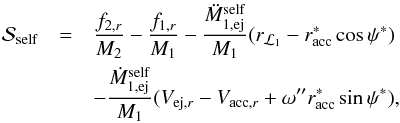 (A.17)and
(A.17)and 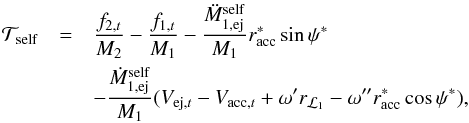 (A.18)which are the same as Eqs. (11) and (12), noting that ω′ = ω′′ = ω for circular orbits. The quantity ψ∗ is the angle between êr and the impact site, and the subscripts “r” and “t” indicate components along êr and êt respectively.
(A.18)which are the same as Eqs. (11) and (12), noting that ω′ = ω′′ = ω for circular orbits. The quantity ψ∗ is the angle between êr and the impact site, and the subscripts “r” and “t” indicate components along êr and êt respectively.
Appendix B: Torque arising from mass transfer, 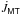
Consider a primary star of mass M1, and a secondary of mass M2, separated by a distance r. They respectively orbit the common centre of mass with an orbital velocity v1 and v2. The velocity of the secondary with respect to the primary is v = v2 − v1, and the orbital angular momentum is given by 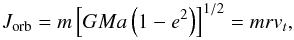 (B.1)where e is the eccentricity, m = M1M2/M is the reduced mass, M = M1 + M2, and vt is the orbital velocity along êt, given by
(B.1)where e is the eccentricity, m = M1M2/M is the reduced mass, M = M1 + M2, and vt is the orbital velocity along êt, given by 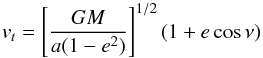 (B.2)and ν is the true anomaly. Taking the time derivative of the last equality in Eq. (B.1) and noting that ṙ = 0 for an osculating orbit (see, e.g. Bonačić Marinović et al. 2008), yields
(B.2)and ν is the true anomaly. Taking the time derivative of the last equality in Eq. (B.1) and noting that ṙ = 0 for an osculating orbit (see, e.g. Bonačić Marinović et al. 2008), yields 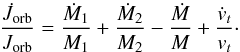 (B.3)Similarly to Eq. (A.16), the equation of motion of a binary acted on by perturbing forces
(B.3)Similarly to Eq. (A.16), the equation of motion of a binary acted on by perturbing forces 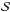 and
and 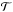 reads
reads 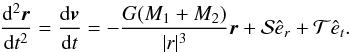 (B.4)Taking the dot product of Eq. (B.4) with êt gives
(B.4)Taking the dot product of Eq. (B.4) with êt gives 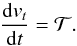 (B.5)Inserting Eqs. (B.5) and (B.2) into Eq. (B.3), and using the first equality in Eq. (B.1), gives the torque applied onto the orbit from mass transfer,
(B.5)Inserting Eqs. (B.5) and (B.2) into Eq. (B.3), and using the first equality in Eq. (B.1), gives the torque applied onto the orbit from mass transfer, 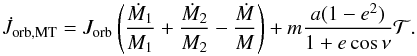 (B.6)The net change of the primary’s mass is the sum of mass transferred to the companion via RLOF,
(B.6)The net change of the primary’s mass is the sum of mass transferred to the companion via RLOF, 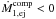 , and mass ejected by the wind, Ṁ1,loss< 0, i.e.
, and mass ejected by the wind, Ṁ1,loss< 0, i.e. 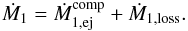 (B.7)Similarly, for the secondary
(B.7)Similarly, for the secondary 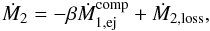 (B.8)where the first term on the right hand side gives the accretion rate and Ṁ2,loss includes the mass ejected from the system during non-conservative mass transfer. Substituting Eqs. (B.7) and (B.8) into Eq. (B.6) gives
(B.8)where the first term on the right hand side gives the accretion rate and Ṁ2,loss includes the mass ejected from the system during non-conservative mass transfer. Substituting Eqs. (B.7) and (B.8) into Eq. (B.6) gives 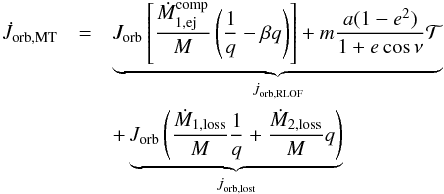 (B.9)where q = M1/M2,
(B.9)where q = M1/M2, 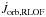 is the torque acting on the orbit as a consequence of RLOF, while
is the torque acting on the orbit as a consequence of RLOF, while 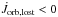 is the torque applied by the material leaving the system. The corresponding torque applied onto the transferred mass is just
is the torque applied by the material leaving the system. The corresponding torque applied onto the transferred mass is just 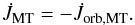 (B.10)Using Eqs. (B.9) and (B.10) with e = 0 gives Eq. (15).
(B.10)Using Eqs. (B.9) and (B.10) with e = 0 gives Eq. (15).
Next, we demonstrate the consistency of Eq. (B.9) by showing that in the classical formalism for conservative mass transfer 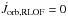 . If all material is transferred to the secondary (αself = 0, β = 1), if the stars are treated as point masses (rℒ1 = 0, racc = 0), and if we neglect the gravitational attraction by the accretion stream (f1 = 0, f2 = 0), Eq. (10) reduces to
. If all material is transferred to the secondary (αself = 0, β = 1), if the stars are treated as point masses (rℒ1 = 0, racc = 0), and if we neglect the gravitational attraction by the accretion stream (f1 = 0, f2 = 0), Eq. (10) reduces to 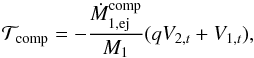 (B.11)where
(B.11)where 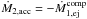 for conservative mass transfer. Sepinsky et al. (2007b) and Luk’yanov (2008) demonstrated that, if the
for conservative mass transfer. Sepinsky et al. (2007b) and Luk’yanov (2008) demonstrated that, if the
orbital angular momentum is conserved, in a circular orbit V1,t and V2,t are related by 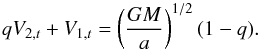 (B.12)Substituting Eq. (B.12) into Eq. (B.11), and that result into Eq. (B.6) gives for a circular orbit
(B.12)Substituting Eq. (B.12) into Eq. (B.11), and that result into Eq. (B.6) gives for a circular orbit  (B.13)where we have used M1/M = q/ (1 + q). Using Eq. (B.1), Eq. (B.13) reduces to zero, as required.
(B.13)where we have used M1/M = q/ (1 + q). Using Eq. (B.1), Eq. (B.13) reduces to zero, as required.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.