| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 17 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201322643 | |
| Published online | 10 July 2014 | |
Online material
Appendix A: Parameter bias
Mass and redshift ranges for the application of the individual correction functions of the parameter bias in case of known cluster redshift.
Parameters of the correction funtion for the simulation with known redshift.
Parameters of the correction funtions for the biases in the temperature and the redshift when the cluster redshift itself is unavailable. For these simulations these biases are independent of the cluster mass.
Within this section we state the estimated correction functions for the parameter bias
and describe for which mass and redshift ranges these corrections apply (Tables A.1–A.3). As
the parameter biases are independent of the cluster mass for the simulations with
unknown redshift, the correction function covers the entire simulated redshift space
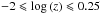 in these cases. The functions
are expressed by Eq. (9) with the
variables A
and B and
present an approximated estimate for the bias correction.
in these cases. The functions
are expressed by Eq. (9) with the
variables A
and B and
present an approximated estimate for the bias correction.
Appendix B: Comparison between different scaling relations
In addition to the comparison of the number of clusters for the scaling relations by Reichert et al. (2011) and Vikhlinin et al. (2009a), we performed a thorough analysis of the distribution of galaxy clusters with mass and redshift for these two relations. For both relations a cosmology of Ωm = 0.3, ΩΛ = 0,7, h = 0.7 and σ8 = 0.795 is assumed. The distribution are presented for three different minimum numbers of detected photons ηmin = 50, 500 and 1500 (Figs. B.1 and B.2). Even though sources with as little as 50 photon counts are assumed to be identified as galaxy clusters, a larger number of counts improves the precision and the accuracy of the reduced cluster properties. The simulation of these distributions follows the analogous setup as described in Sect. 4.
With an increasing value for ηmin, the total number of detected clusters declines significantly as the distribution of clusters becomes shallower and the low and intermediate mass clusters are no longer detected at the high redshifts. According to this, the total number of detected clusters decreases from 113 400 for ηmin = 50 to 11 000 for ηmin = 500 and to 3000 for ηmin = 1500. At the same time, the maximum of the distribution shifts to lower redshift values z< 0.3. In comparison, both scaling relations yield the same position of the maximum of the distribution, where the distribution based on the scaling relation by Reichert et al. (2011) displays a broader peak. This development results in a total number of clusters, which is 15–20% above the value for the study of the scaling relation by Vikhlinin et al. (2009a) with a total number of cluster of 103 700 for ηmin = 50, 8900 for ηmin = 500 and 2300 for ηmin = 1500.
This analysis emphasises the strong dependence of the distribution of clusters and of the total number of detected clusters on the applied scaling relations and the defined minimum number of photons ηmin.
 |
Fig. B.1
Distribution of galaxy clusters with mass and redshift for three different photon detection minimums ηmin = 50, 500 and 1500 from top to bottom for the scaling relation by Reichert et al. (2011). All plots are generated for a lower mass cut of M = 5 × 1013/h100 M⊙ with h100 = 0.7. The colour indicates the number of detected clusters in the individual bins in units of log 10, where the cluster mass is considered in units of log (M/M⊙). The total number of detected clusters reads from top to bottom Ncluster = 113 400, 11 000 and 3000. |
| Open with DEXTER | |
 |
Fig. B.2
Distribution of galaxy clusters with mass and redshift for three different photon detection minimums ηmin = 50,500 and 1500, when applying the scaling relations by (Vikhlinin et al. 2009a). All plots are generated for a lower mass cut of M = 5 × 1013/h100 M⊙ with h100 = 0.70, where the labeling is equivalent to Fig. B.1. The total number of detected clusters reads from top to bottom Ncluster = 103 700, 8900 and 2300. |
| Open with DEXTER | |
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


