| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201423409 | |
| Published online | 13 May 2014 | |
Online material
Appendix A: Results of Tests A, B, C1 and C2
Appendix A.1: Test A
The goal of this test is to assess the impact of redshift measurement errors on the counts in cells. Results are shown in Fig. A.1. The ZADE and cloning methods do not correct for spectroscopic redshift error, so for this test we only compare the WF and LNP methods.
 |
Fig. A.1
As in Fig. 5, but for Test A. ZADE and
cloning are not used. |
| Open with DEXTER | |
 |
Fig. A.2
As in Fig. 5, but for Test B. |
| Open with DEXTER | |
 |
Fig. A.3
As in Fig. 5, but for Test C1. In this test the cloning method is not used (see text for details). |
| Open with DEXTER | |
 |
Fig. A.4
As in Fig. 5, but for Test C2. In this test the cloning method is not used (see text for details). |
| Open with DEXTER | |
First, we verified the effects of the spectroscopic redshift error on the counts in
cell when no attempt is made to correct for it (left panel in Fig. A.1): this error does not induce systematic errors
in regions of low/mean density (1+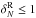 ), while it systematically
makes us underestimate the counts at high densities (by ~8% for R5 and
~3% for R8, for
), while it systematically
makes us underestimate the counts at high densities (by ~8% for R5 and
~3% for R8, for
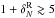 ).
Random and systematic errors are significantly smaller for R8 than for
R5, i.e. when the size of the cell is
larger than the linear scale associated with the redshift error. For both radii, the
systematic error is comparable to the scatter.
).
Random and systematic errors are significantly smaller for R8 than for
R5, i.e. when the size of the cell is
larger than the linear scale associated with the redshift error. For both radii, the
systematic error is comparable to the scatter.
Applying the WF method to recover the counts in the reference catalogue does not improve the reconstruction, or even increases (almost double) the systematic error at high density for R5. Applying the LNP method, the systematic error for R5 slightly increases at high density (becoming ~10%), but disappears for R8 (but at the expense of a larger random error, that approaches ~10%). Both estimates effectively smooth the density field, and thus the extremes of the density field are systematically underestimated, especially on smaller scales. For the WF method, the systematic error is comparable to the scatter, while for the LNP it is ~50% smaller, for both R5 and R8.
Even though our aim is to reconstruct counts in redshift space, we also compared the counts in Test A with a reference mock catalogue in real space to check the effect of peculiar velocities. As expected, with respect to the results of Test A in redshift space, there is a further under-estimation of high densities, and the scatter at low densities is larger, because the cell radii that we use are close to the order of magnitude of peculiar velocities.
Appendix A.2: Test B
This test is designed to assess the impact of gaps in the galaxy distribution. Our gaps are a combination of the cross-shaped regions that reflect the footprint of the VIMOS spectrograph and the empty regions corresponding to missing quadrants.
We applied all four methods described in Sect. 3 to reconstruct the counts in cells, as shown in Fig. A.2. For all methods, the scatter is larger than found in Test A, while the systematic error is comparable. The accuracy of the reconstruction increases when one considers cells with R8.
The ZADE method shows the smallest scatter with low systematic error for both cases R5 and R8. In all cases, the scatter around the systematic error decreases for higher densities.
In this test, the ZADE method performs better than cloning and outperforms the WF and LNP reconstructions. We attribute this to the effective smoothing scale adopted in the WF and LNP methods. Small-scale structures are lost in the filtered fields even within quadrants that are sampled at 100%. The effect of the smoothing is greater for R5, and the density is systematically underestimated. The LNP method shows the largest scatter around the mean, but its systematic error goes to zero for the highest densities, which does not happen for the other methods.
It is interesting to notice that for high counts, all the methods tend to
underestimate the counts in the reference catalogue, while all (but cloning) tend to
overestimate it for the lowest counts. The cloning method is the only one that gives
unbiased average counts for the lowest value of
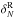 .
.
Appendix A.3: Tests C1 and C2
With Test C1 we want to assess the effects of a low sampling rate, homogeneous over the entire VIPERS field. With Test C2, we implement in the mocks the variation in the sampling rate as a function of quadrant, keeping the average value as in Test C1. We used the methods WF, LNP, and ZADE, and the results are shown in Figs. A.3 and A.4. We did not use cloning to correct for low sampling rate for the reasons described in Sect. 3.2.
In the case of Test C1, it is evident from Fig. A.3 that the density in the reference catalogue is overestimated for the lowest counts and underestimated (up to ~20% for LNP and ZADE for the case of R5) for large counts. In general, the scatter is larger than or comparable to the systematic error, possibly with the exception of the highest densities, as the scatter decreases for higher densities. For all three methods, and for both R5 and R8, the systematic error and the scatter due to low sampling rate are larger than those due to gaps, and much larger than those due to the spectroscopic redshift error. The relative importance of these error sources depends of course on the survey characteristics. In the case of VIPERS, where the gaps cover ~25% of the observed areas while the sampling rate is at the level of 35%, the second effect is bound to dominate the error budget. Spectroscopic redshift errors are marginal on the scales of the cells considered here. We verified that, keeping the dimension of the gaps fixed (~25%) and progressively reducing the sampling rate from 100% in steps of 10%, the systematic error due to low sampling rate becomes comparable to the one due to gaps (Test B) at a sampling rate of ~60%.
Figure A.4 shows that the results for Test C2 are only slightly worse than those of Test C1, for both the amplitude of the systematic error and the scatter. This confirms that in VIPERS the major source of uncertainty in counts in cells is the low (~35%) sampling rate.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.