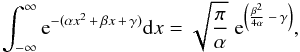| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 14 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201323037 | |
| Published online | 03 April 2014 | |
Online material
Appendix A: Cartesian to galactic coordinate transformation
The spatial distribution of the cluster is given in Cartesian coordinates by a Gaussian distribution in each axis:  where X0, Y0, and Z0 define the centre of the cluster in each axis, and σS gives the variance of the distribution.
where X0, Y0, and Z0 define the centre of the cluster in each axis, and σS gives the variance of the distribution.
To transform this Cartesian PDF into polar coordinates as required for our observables r, l, and b, we start with the relationship between our two sets of variables and find the inverse:
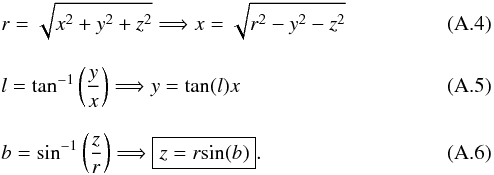 Then we have two equations and two unknowns:
Then we have two equations and two unknowns: 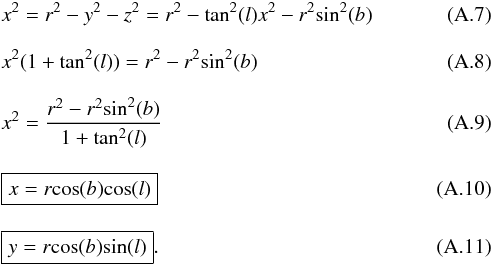 Then we require the Jacobian: r2cos(b).
Then we require the Jacobian: r2cos(b).
By substituting the x, y, and z found above into the original PDF and multiplying by the Jacobian of the transformation, we find the PDF in the new coordinate system: 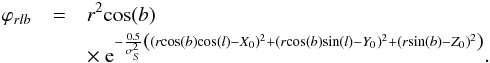 (A.12)By rotating our coordinate system l,b → l′,b′ to align the cluster centre with the X axis, we have new coordinates l′ and b′ for all the stars. In this rotated coordinate system, the cluster has a position
(A.12)By rotating our coordinate system l,b → l′,b′ to align the cluster centre with the X axis, we have new coordinates l′ and b′ for all the stars. In this rotated coordinate system, the cluster has a position 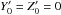 , and X′ is equivalent to the distance to the clusters centre. The above spatial probability distribution function can then be simplified as
, and X′ is equivalent to the distance to the clusters centre. The above spatial probability distribution function can then be simplified as 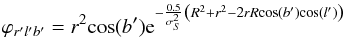 (A.13)where R is the distance to the cluster.
(A.13)where R is the distance to the cluster.
It should be noted that the two coordinate systems are used simultaneously. The rotated coordinates (l′,b′) are used in the integration over position to simplify the integrals as explained above. However, in the analytic solution to the integrals over μα∗μδvr, the unrotated coordinates l and b are used.
Appendix B: Integration of the likelihood function
To evaluate 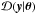 in Eq. (1) we must integrate over all y0, giving a multiple integral that can be split into three parts. First is the integral over variables with assumed zero error, second kinematics, and finally distance.
in Eq. (1) we must integrate over all y0, giving a multiple integral that can be split into three parts. First is the integral over variables with assumed zero error, second kinematics, and finally distance.
Appendix B.1: Integration over m0, l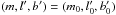 and b
and b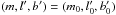
As these variables have errors given by the delta function, 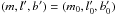 so we can use (m,l′,b′). This avoids integrating over these three parameters.
so we can use (m,l′,b′). This avoids integrating over these three parameters.
Appendix B.2: Integration over μα∗,0, μδ,0 and vr0
The triple integral over μα∗,0, μδ,0 and vr0 is
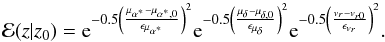 (B.1)where
(B.1)where 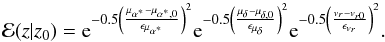 (B.2)In order to perform the integral, the function ϕv(U,V,W) must be expressed in terms of μα∗,0, μδ,0, and vr0. This is achieved through the following expressions:
(B.2)In order to perform the integral, the function ϕv(U,V,W) must be expressed in terms of μα∗,0, μδ,0, and vr0. This is achieved through the following expressions:
Therefore ϕv(U,V,W) can be written in terms of μα∗,0, μδ,0 and vr0 as 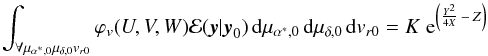 (B.6)This can be integrated using the definite integral,
(B.6)This can be integrated using the definite integral, 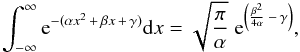 (B.7)giving the solution
(B.7)giving the solution 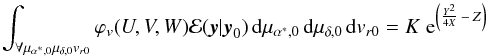 (B.8)where K, X, Y, and Z are defined in Eq. (B.10).
(B.8)where K, X, Y, and Z are defined in Eq. (B.10).
Appendix B.3: Integration over R
The remaining integral has no analytical solution and will therefore be performed numerically:
Appendix C: Normalisation coefficient
Until now we have been using the un-normalised joint probability distribution. Normalisation is achieved by dividing by a normalisation constant, 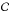 . The normalisation constant is found by integrating the un-normalised joint probability distribution
. The normalisation constant is found by integrating the un-normalised joint probability distribution 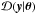 over all y:
over all y: 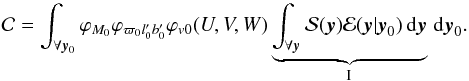 (C.1)This integral can be performed in two parts, where I is defined such that
(C.1)This integral can be performed in two parts, where I is defined such that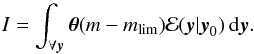 (C.2)Substituting in the selection function
(C.2)Substituting in the selection function 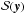 and the PDF of the observational errors ℰ(y | y0) gives the following seven-dimensional integral:
and the PDF of the observational errors ℰ(y | y0) gives the following seven-dimensional integral: 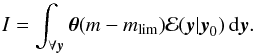 (C.3)This integral can be split into two parts. The integral over the delta function in ℰ(y | y0) that, by definition, gives one; and the integral over each Gaussian error,
(C.3)This integral can be split into two parts. The integral over the delta function in ℰ(y | y0) that, by definition, gives one; and the integral over each Gaussian error, 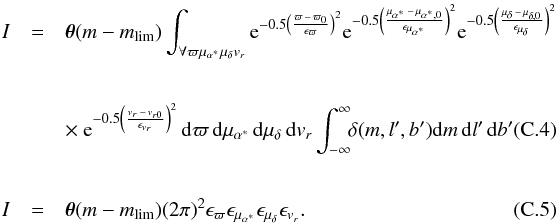 Here, θ(m − mlim) acts to provide an upper limit to the integral over all MG. Substituting I back into C we have
Here, θ(m − mlim) acts to provide an upper limit to the integral over all MG. Substituting I back into C we have 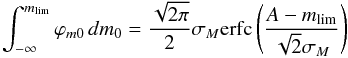 (C.6)As with in the previous section, the integral can be split up into a number of parts.
(C.6)As with in the previous section, the integral can be split up into a number of parts.
Appendix C.1: Integration over MG
Evaluating first the integral over apparent magnitude gives 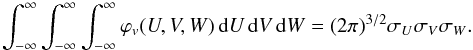 (C.7)
(C.7)
where erfc is the complementary error function, and 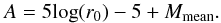 (C.8)
(C.8)
Appendix C.2: Integration over (U,V,W)
Integrating over (U,V,W) gives 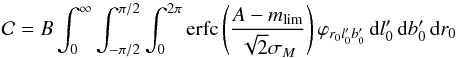 (C.9)
(C.9)
Appendix C.3: Integration over l , b
, b , and r0
, and r0
The remaining triple integral has no analytical solution and will be performed numerically:  (C.10)with:
(C.10)with: 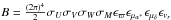 .
.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.