| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322474 | |
| Published online | 17 April 2014 | |
Online material
Appendix A: Maximum likelihood estimation of the cosmic variance σv
Maximum likelihood estimators (MLEs) have been used in a wide range of topics in astrophysics. For example, Naylor & Jeffries (2006) used a MLE to fit colour-magnitude diagrams, Arzner et al. (2007) to improve the determination of faint X-ray spectra, Makarov et al. (2006) to improve distance estimates using red giant branch stars, and López-Sanjuan et al. (2008, 2009a,b, 2010b) to estimate reliable merger fractions from morphological criteria. The MLEs are based on the estimation of the most probable values of a set of parameters, which define the probability distribution that describes an observational sample.
The general MLE operates as follows. Throughout this Appendix, we denote the
probability to obtain the values a given the parameters b as P (a |
b). Being xj the measured
values in the ALHAMBRA field j, and θ the parameters that we want to estimate, we may
express the joined likelihood function as 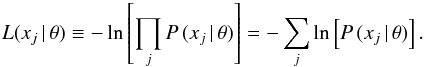 (A.1)If we are able to
express P
(xj |
θ) analytically, we can minimise Eq. (A.1) to obtain the best estimation of the
parameters θ, as denoted as θML. In our
case, xj is the observed
value of the merger fraction in log-space for the ALHAMBRA sub-field j, where
(A.1)If we are able to
express P
(xj |
θ) analytically, we can minimise Eq. (A.1) to obtain the best estimation of the
parameters θ, as denoted as θML. In our
case, xj is the observed
value of the merger fraction in log-space for the ALHAMBRA sub-field j, where
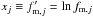 . We
decided to work in log-space because that makes the problem analytic and simplifies the
implementation of the method without losing mathematical rigour.
. We
decided to work in log-space because that makes the problem analytic and simplifies the
implementation of the method without losing mathematical rigour.
The ALHAMBRA sub-fields are assumed to have a real merger fraction (not affected by
observational errors) that define a Gaussian distribution in log-space,
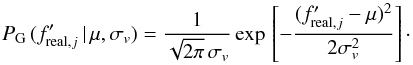 (A.2)Observational errors
cause the observed
(A.2)Observational errors
cause the observed 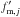 to differ
from their respective real values
to differ
from their respective real values 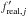 . The
observed
. The
observed 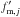 are
assumed to be extracted for a Gaussian distribution with mean
are
assumed to be extracted for a Gaussian distribution with mean
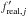 and
standard deviation σo,j (the
observational errors),
and
standard deviation σo,j (the
observational errors), 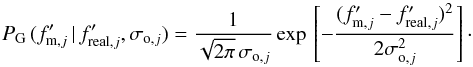 (A.3)We assumed that the
observational errors are Gaussian in log-space, or, that they are log-normal in
observational space. This is a good approximation of the reality because we are dealing
with fractions that cannot be negative and that have asymmetric confidence intervals, as
shown by Cameron (2011). In our case, we
estimated the observational errors in log-space as σo =
σf/fm.
We checked that the values of σo derived from our jackknife errors
are similar to those estimated from the Bayesian approach in Cameron (2011) with a difference between them ≲15%.
(A.3)We assumed that the
observational errors are Gaussian in log-space, or, that they are log-normal in
observational space. This is a good approximation of the reality because we are dealing
with fractions that cannot be negative and that have asymmetric confidence intervals, as
shown by Cameron (2011). In our case, we
estimated the observational errors in log-space as σo =
σf/fm.
We checked that the values of σo derived from our jackknife errors
are similar to those estimated from the Bayesian approach in Cameron (2011) with a difference between them ≲15%.
We obtained the probability P (xj |
θ) of each ALHAMBRA sub-field by the total
probability theorem: 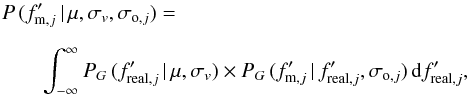 (A.4)where
(A.4)where
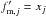 and (μ,σv,σo,j)
= θ in Eq. (A.1). Note that the values of σo,j are the measured
uncertainties for each ALHAMBRA sub-field, so the only unknowns are the variables
μ and
σv, which we want to
estimate. Note also that we integrate over the variable
and (μ,σv,σo,j)
= θ in Eq. (A.1). Note that the values of σo,j are the measured
uncertainties for each ALHAMBRA sub-field, so the only unknowns are the variables
μ and
σv, which we want to
estimate. Note also that we integrate over the variable
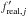 , so we
are not be able to estimate the real merger fractions individually, but only the
underlying Gaussian distribution that describes the sample.
, so we
are not be able to estimate the real merger fractions individually, but only the
underlying Gaussian distribution that describes the sample.
The final joined likelihood function, Eq. (A.1) after integrating Eq. (A.4), is 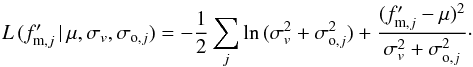 (A.5)With the minimisation
of this function, we obtain the best estimation of both μ and the cosmic variance
σv, which are
unaffected by observational errors.
(A.5)With the minimisation
of this function, we obtain the best estimation of both μ and the cosmic variance
σv, which are
unaffected by observational errors.
In addition, we can analytically estimate the errors in the parameters above. We can
obtain those via an expansion of the function 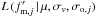 in a Taylor’s series of its
variables θ =
(μ,σv,σo,j)
around the minimisation point θML. The previous minimisation process
made the first L derivative null, and we obtain
in a Taylor’s series of its
variables θ =
(μ,σv,σo,j)
around the minimisation point θML. The previous minimisation process
made the first L derivative null, and we obtain
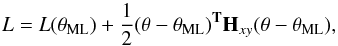 (A.6)where Hxy is the Hessian matrix,
and T denotes
the transpose matrix. The inverse of the Hessian matrix provides an estimate of the 68%
confidence intervals of μML and σML, as well
as the covariance between them. The Hessian matrix of the joined likelihood function
L is
defined as
(A.6)where Hxy is the Hessian matrix,
and T denotes
the transpose matrix. The inverse of the Hessian matrix provides an estimate of the 68%
confidence intervals of μML and σML, as well
as the covariance between them. The Hessian matrix of the joined likelihood function
L is
defined as 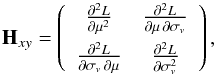 (A.7)with
(A.7)with
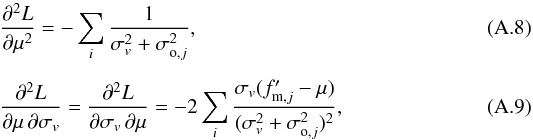 and
and
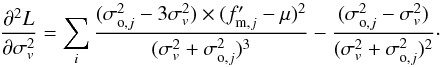 (A.10)Then, we computed the
inverse of the minus Hessian, hxy = ( −
Hxy)-1.
Finally, we estimated the variances of our inferred parameters as
(A.10)Then, we computed the
inverse of the minus Hessian, hxy = ( −
Hxy)-1.
Finally, we estimated the variances of our inferred parameters as
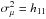 and
and
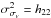 because maximum
likelihood theory states that
because maximum
likelihood theory states that 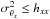 .
.
 |
Fig. A.1
Recovered cosmic variance over input cosmic variance (top panel)
and median σσv
over the dispersion of the recovered cosmic variance (bottom
panel) as a function of Δσ. In both panels, triangles, circles, and
squares are the results from synthetic catalogues with n =
50,250, and 1000, respectively. White symbols
show the results from the BLS fit to the data (σv,BLS), while
those coloured show the ones from the MLE (σv,ML). The
n =
50 and 1000 points are shifted to avoid overlap. The dashed
lines mark identity, and the solid line in the top panel shows
the expectation from a convolution of two Gaussians in log-space,
|
| Open with DEXTER | |
We tested the performance and the limitations of our MLE through synthetic catalogues of merger fractions. We created several sets of 1000 synthetic catalogues with each of them composed by a number n of merger fractions randomly drawn from a log-normal distribution with μin = log 0.05 and σv,in = 0.2 and affected by observational errors σo. We explored the n = 50,250 and 1000 cases for the number of merger fractions and varied the observational errors from σo = 0.1 to 0.5 in 0.1 steps. That is, we explored observational errors in the measurement of the merger fraction from Δσ ≡ σo/σv = 0.5 to 2.5 times the cosmic variance that we want to measure. We checked that the results below are similar for any value of σv,in. We find that
-
1.
The median value of the recovered μ, as noted
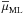 , in
each set of synthetic catalogues is similar to μin,
with deviations lower than 0.5% in all cases under study. However, we find that
, in
each set of synthetic catalogues is similar to μin,
with deviations lower than 0.5% in all cases under study. However, we find that
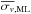 for n =
50 catalogues overestimates σv,in more than
5% at Δσ ≳
2.0, while we recover σv,in well even
with Δσ =
2.5 (Fig. A.1, top panel)
for n =
1000. This means that larger data sets are needed to recover
the underlying distribution as the observational errors increase.
for n =
50 catalogues overestimates σv,in more than
5% at Δσ ≳
2.0, while we recover σv,in well even
with Δσ =
2.5 (Fig. A.1, top panel)
for n =
1000. This means that larger data sets are needed to recover
the underlying distribution as the observational errors increase. -
2.
We also study the values recovered by a best least-squares (BLS) fit of Eq. (18) to the synthetic catalogues. We find that (i) the BLS fit recovers the right values of μin. This was expected, since the applied observational errors preserve the median of the initial distribution. (ii) The BLS fit overestimates σv,in in all cases. The recovered values depart from the initial one as expected from a convolution of two Gaussians with a variance σv,in and σo, where
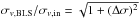 .
The MLE performs a de-convolution of the observational errors, recovering
accurately the initial cosmic variance (Fig. A.1, top panel).
.
The MLE performs a de-convolution of the observational errors, recovering
accurately the initial cosmic variance (Fig. A.1, top panel). -
3.
The estimated variances of μ and σv are reliable. That is, the median variances
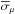 and
and
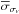 estimated by the MLE are similar to the dispersion of the recovered values, as
noted sμ and
sσv,
in each set of synthetic catalogues. The difference between both variances for
μ
is lower than 5% in
all the probed cases. However, we find that
estimated by the MLE are similar to the dispersion of the recovered values, as
noted sμ and
sσv,
in each set of synthetic catalogues. The difference between both variances for
μ
is lower than 5% in
all the probed cases. However, we find that
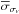 for n =
50 catalogues overestimates sσv,
which is more than 5% at Δσ ≳ 1.5: this is the limit of the MLE to
estimate reliable uncertainties with this number of data (Fig. A.1, bottom panel). Because the estimated
variance tends asymptotically to sσv
for a large number of data,
for n =
50 catalogues overestimates sσv,
which is more than 5% at Δσ ≳ 1.5: this is the limit of the MLE to
estimate reliable uncertainties with this number of data (Fig. A.1, bottom panel). Because the estimated
variance tends asymptotically to sσv
for a large number of data, 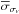 for n =
1000 catalogues deviates less from the expected value than for
n =
50 synthetic catalogues. Note that the value of σv is still
unbiased as such large observational errors (Fig. A.1, top panel), when the estimated variance σσv
deviates from the expectations at large Δσ, and we can roughly estimate
σσv
through realistic synthetic catalogues as those in this Appendix.
for n =
1000 catalogues deviates less from the expected value than for
n =
50 synthetic catalogues. Note that the value of σv is still
unbiased as such large observational errors (Fig. A.1, top panel), when the estimated variance σσv
deviates from the expectations at large Δσ, and we can roughly estimate
σσv
through realistic synthetic catalogues as those in this Appendix. -
4.
The variances of the recovered parameters decreases with n and increases with σo. That reflects the loss of information due to the observational errors. Remark that the MLE takes these observational errors into account to estimate the parameters and their variance.
We conclude that the MLE developed in this Appendix is not biased, providing accurate
variances, and we can recover reliable uncertainties of the cosmic variance
σv in ALHAMBRA
(n = 48)
for Δσ ≲
1.5. Note that reliable values of σv in ALHAMBRA are
recovered at Δσ ≲
2.0. We checked that the average Δσ in our study is 0.60
(the average observational error is 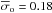 ),
and the maximum value is Δσ
= 0.85. Thus, the results in the present paper are robust against the
effect of observational errors.
),
and the maximum value is Δσ
= 0.85. Thus, the results in the present paper are robust against the
effect of observational errors.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


