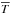| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 15 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201321911 | |
| Published online | 28 March 2014 | |
Online material
Appendix A: Opacity law in the buffer zones
Here, we give the functional form of σ we used to prevent the temperature to drop at the inner edge of the simulation. 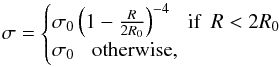 (A.1)where σ0 stands for σhot or σcold depending on the model. The value of σ is kept constant in the outer buffer.
(A.1)where σ0 stands for σhot or σcold depending on the model. The value of σ is kept constant in the outer buffer.
Appendix B: Wave heating
The large-scale density waves witnessed in our simulations develop weak-shock profiles, which are controlled by a competition between nonlinear steepening and wave dispersion. Keplerian shear may also play a role as it “winds up” the spiral and decreases the radial wavelength; though by the time this is important most of the wave energy has already dissipated.
A crude model that omits the strong dispersion inherent in our large-scale density waves nevertheless can successfully account for the energy dissipation in the simulations. In such a model the density wave profiles are dominated by steepening and can thus be approximated by a sawtooth shape propagating at the sound speed velocity cs (see Fig. B.1). The evolution of the amplitude of such isentropic waves is given by Landau & Lifshitz (1959). In the wave frame of reference, the gas velocity at the shock crest evolves over time as the shock wave dissipates: 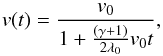 (B.1)where v0 is the excitation amplitude of the wave and λ0 its wavelength, assumed to be conserved over the wave propagation. The mean mechanical energy embodied in one wave period at time t is given by an integral over radius:
(B.1)where v0 is the excitation amplitude of the wave and λ0 its wavelength, assumed to be conserved over the wave propagation. The mean mechanical energy embodied in one wave period at time t is given by an integral over radius: 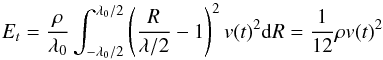 (B.2)where λ is the wavelength at time t. We next compute the mechanical energy radial flux through a unit surface:
(B.2)where λ is the wavelength at time t. We next compute the mechanical energy radial flux through a unit surface: 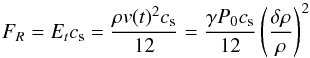 (B.3)where δρ is the difference between the shocked and pre-shocked density. To compute the last equality, we have used the fact that, under the weak shock approximation, the wave evolution is isentropic and thus δρ/ρ = v/cs (Landau & Lifshitz 1959). The wave energy and its flux are related through the following conservation law:
(B.3)where δρ is the difference between the shocked and pre-shocked density. To compute the last equality, we have used the fact that, under the weak shock approximation, the wave evolution is isentropic and thus δρ/ρ = v/cs (Landau & Lifshitz 1959). The wave energy and its flux are related through the following conservation law: 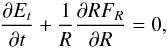 (B.4)while the dissipation rate of the wave is expressed using the mechanical energy conversion into heat per unit time:
(B.4)while the dissipation rate of the wave is expressed using the mechanical energy conversion into heat per unit time: 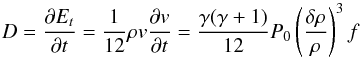 (B.5)where f = cs/λ0 is the wave frequency. We used the density fluctuations in our simulations as the difference between the shocked and pre-shocked density to estimate the local wave heating in Eq. (27).
(B.5)where f = cs/λ0 is the wave frequency. We used the density fluctuations in our simulations as the difference between the shocked and pre-shocked density to estimate the local wave heating in Eq. (27).
 |
Fig. B.1
Velocity fluctuations profile: series of “teeth” modelling the wave shocks. |
| Open with DEXTER | |
In addition to that estimate, the thermal energy flux divergence can be used, through Eq. (B.4), as a way to estimate the radial variation of the wave amplitude: 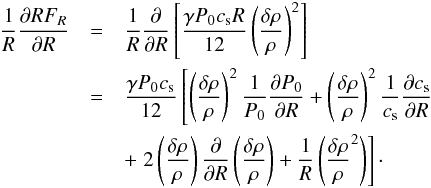 (B.6)This must equal the energy rate released as thermal heat given by −D. Combining the last two expression thus provides an expression for the radial decay of the wave amplitude:
(B.6)This must equal the energy rate released as thermal heat given by −D. Combining the last two expression thus provides an expression for the radial decay of the wave amplitude: 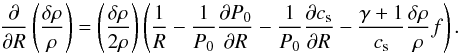 (B.7)The first term is the geometrical term that described the wave dilution as it propagates cylindrically. The second and third terms are specific to waves propagating in stratified media where mean pressure and sound speed are not uniform. Finally, the last term of the right hand side of this equation reflects the wave damping by shocks. In our simulations, all four terms are of comparable importance.
(B.7)The first term is the geometrical term that described the wave dilution as it propagates cylindrically. The second and third terms are specific to waves propagating in stratified media where mean pressure and sound speed are not uniform. Finally, the last term of the right hand side of this equation reflects the wave damping by shocks. In our simulations, all four terms are of comparable importance.
Appendix C: Model with an extended radial extent
In this section of the appendix we describe the results obtained in the radially extended σhot run. We initiated MHD turbulence in that model in the absence of any dissipative term until the region between R = 1 and R = 3.5 has reached thermal equilibrium (t = 900). At that point, we set η0 = 10-3 for R ≥ 3.5. As expected, a dead zone quickly appeared at those radii. Because of the prohibitic computational coast of that simulation (there are 960 cells in the radial direction!), we were not able to run that model until thermal equilibrium is established at all radii. Indeed, the cooling time becomes very long at large radius. Instead, we followed the time evolution of the temperature at nine locations in the dead zone. Due to the absence of turbulent heating, we found that the temperature slowly decreases with time. Assuming this decrease is due to a combination of cooling (resulting from the cooling function) and wave heating, it can be modelled using the following differential equation 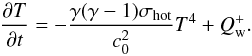 (C.1)where the term
(C.1)where the term 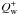 accounts for the (unknown) wave heating. We fitted the time evolution of the temperature during the duration of the simulation (~1000 orbits) in order to obtain a numerical estimate of
accounts for the (unknown) wave heating. We fitted the time evolution of the temperature during the duration of the simulation (~1000 orbits) in order to obtain a numerical estimate of 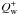 at those nine locations. An example of that fit is provided in the insert of Fig. C.1. Using these value, we can obtain an estimate for the equilibrium temperature in the dead zone, as shown in Fig. C.1. The comparison with the estimate of Eq. (28) provided by the black line is excellent everywhere in the dead zone.
at those nine locations. An example of that fit is provided in the insert of Fig. C.1. Using these value, we can obtain an estimate for the equilibrium temperature in the dead zone, as shown in Fig. C.1. The comparison with the estimate of Eq. (28) provided by the black line is excellent everywhere in the dead zone.
As a sanity check, we test here if the wave amplitude decreases as their energy content is converted into heat. We show in Fig. C.2 the mean density fluctuation profile obtained in the extended σhot simulation. It exhibits two maxima close to the dead zone inner edge located at R(g,1) and R(g,2) and the amplitude decay with radius. The reason why we see two such maxima is not clear but might be due to waves originated at the dead/active interface as well as waves excited as the location of the pressure maximum. In any case, we found that modelling the amplitude of fluctuations as the signature of a combination of two waves generated at R(g,i) gives acceptable results. We use an explicit scheme to numerically integrate Eq. (B.7) from the wave generation locations R(g,i). The two waves are excited with the amplitude measured at R = R(g,i) with the frequency 1/f = 0.15τcool(R(g,i)). We plot the solution thus obtained in Fig. C.2. The good agreement between the analytical solution and the profile gives a final confirmation that waves control the dead zone thermodynamics.
 |
Fig. C.1
Temperature profile ⟨ T ⟩ averaged over 200 orbits after t = 900 + τcool(R = 7) obtained in the extended σhot case. The black line show wave-equilibrium temperature profile. Red dots show the extrapolated temperature for 7 radii. The inserted frame show in red the temperature evolution |
| Open with DEXTER | |
 |
Fig. C.2
Profile of density standard deviation ⟨ δρ ⟩ averaged over 200 inner orbits after t = 900 + τcool(R = 7) in the extended σhot case. The black plain line shows the density fluctuation amplitude deducted from the two waves model. The excitation locations used in the two waves model are shown by blue dashed lines. |
| Open with DEXTER | |
Appendix D: Simulation with a higher resolution
Here we present a brief test of the impact of spatial resolution on our results. We have restarted the σhot run from the thermal equilibrium of the ideal MHD case (t = 600) and the static dead zone case (t = 900), with twice as many cells in each direction. The resolution is (640,160,160). We show the averaged temperature profile of both cases in Fig. D.1. Because of the large computational cost, each models are integrated for 200 orbits and time averages are only performed over the last 100 orbits. The temperature profiles of each case are very close to those obtained with the fiducial runs. We conclude that resolution as little impact on our results.
 |
Fig. D.1
Profiles of temperature ⟨ T ⟩ averaged over 100 inner orbits after t = 700 and t = 1000 in the highly resolved σhot case (plain lines). The dashed lines remind the temperature profiles obtained with the low resolution run. For both resolutions, the temperature in the ideal case is shown by a red line and the temperature in the static dead zone case is shown by a black line. |
| Open with DEXTER | |
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.