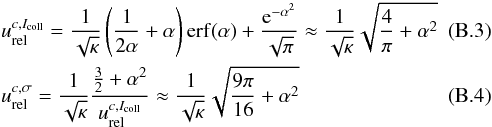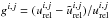| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321151 | |
| Published online | 14 March 2014 | |
Online material
Appendix A: Set of MHD equations
A general set of the Eulerian continuity-, momentum-, and energy equations is the
following (see e.g. Boyd & Sanderson
2003): 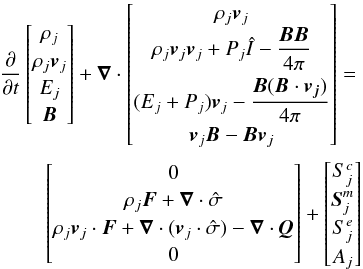 (A.1)
(A.1)
-
vj= fluid velocity
-
ρj= fluid density
-
Ej= internal energy of fluid
-
Pj= pressure of fluid
-
Î= unit tensor
-
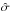 =
viscosity/stress tensor
=
viscosity/stress tensor -
F= external force per unit mass and volume
-
Q= heat flow
-
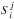 =
sources and sinks
=
sources and sinks -
Aj= ambipolar diffusion between ions and neutrals
where the index j ∈ { H,H+,He,He+,He+ +,i,n }. As discussed above for the index j of the ionized fluid, the density is the sum of all densities of ionized species, the total pressure Pj = ∑ kPk, the total energy Ej = ∑ kEk, with k ∈ {H+, He+, He+ + }.
The force densities, stress tensor and the heat transport on the right-hand side of Eq.
(A.1) are usually neglected in
modeling the large-scale structure of the heliosphere, that is,
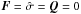 .
While external forces, such as solar gravitation, can be neglected, the stress tensor
.
While external forces, such as solar gravitation, can be neglected, the stress tensor
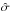 will play an important role in studying the details of the termination shock or
heliopause structure, but to our knowledge this was not discussed so far. Especially the
heat transport by electrons can be expected to be significant, because of the high
thermal speed of these particles, and will be analyzed in future work. If the right-hand
side of Eq. (A.1) vanishes, the set of
equations is called ideal MHD.
will play an important role in studying the details of the termination shock or
heliopause structure, but to our knowledge this was not discussed so far. Especially the
heat transport by electrons can be expected to be significant, because of the high
thermal speed of these particles, and will be analyzed in future work. If the right-hand
side of Eq. (A.1) vanishes, the set of
equations is called ideal MHD.
From Eq. (27) it is evident that the interstellar helium contributes about 40% to the total mass density, thus the total mass density ρn in the above neutral continuity equation is ρn = ρH + ρHe ≈ 1.4ρH. This results in an increased ram pressure and momentum flow ρnvn. Together with the total pressure Pn = PH + PHe = κ(nHTH + nHeTHe) and the previously made assumption TH = THe and nHe = 0.1nH yields Pn = 1.1PH. These estimates show, that helium contributions are not negligible. A similar consideration holds for the governing equations of the charged particles.
If the helium inflow velocity differs in direction from that of hydrogen (Lallement et al. 2005), helium has to be treated as a separate fluid and an additional complete set of the Euler-equations must be solved. If one can assume that the flow velocities of the neutrals and charged fluids are the same for all neutral and ionized species, it is sufficient to solve the two governing equations and treat the other species as tracer particles to calculate their densities and thermal pressures.
Handling the neutrals with a kinetic set of equations (Izmodenov 2007; Heerikhuisen et al.
2008) requires a similar approach for the collision integrals (see Eqs. (39) and (40)) to obtain the balance terms
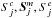 for the
(M)HD equations of charged particles, when including heavier ions.
for the
(M)HD equations of charged particles, when including heavier ions.
Appendix B: “Collision” speeds
For the interaction of particles with different masses (nonresonant charge exchange processes), the approach by McNutt et al. (1998) can be applied. Nevertheless, the relative velocities for the momentum exchange differ from those for the energy exchange, in contrast to what was discussed in McNutt et al. (1998)
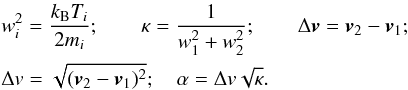 As
described in Eqs. (57) to (60) in McNutt et al.
(1998), the relative speeds for the cross-sections for charge exchange differ
for all three Euler equations, as well as the speeds needed for the charge exchange
cross-section. The speeds are denoted as above
As
described in Eqs. (57) to (60) in McNutt et al.
(1998), the relative speeds for the cross-sections for charge exchange differ
for all three Euler equations, as well as the speeds needed for the charge exchange
cross-section. The speeds are denoted as above 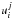 , where
j ∈ {c, m, e, P} for the
continuity, momentum, and energy equations and j = P
for the thermal pressure, respectively. The governing energy equation contains the ram
pressure and the thermal pressure, which are both influenced. The balance equations only
contain the thermal pressure, because changes in the ram pressure or bulk speed are
calculated in the governing equations with the assumption that all species flow with the
same speed. The indices i ∈ {cx, rel} are the speeds
needed for the charge exchange cross-section and corresponding relative speeds. With the
definitions from McNutt et al. (1998) we have to
solve the following type of integrals:
, where
j ∈ {c, m, e, P} for the
continuity, momentum, and energy equations and j = P
for the thermal pressure, respectively. The governing energy equation contains the ram
pressure and the thermal pressure, which are both influenced. The balance equations only
contain the thermal pressure, because changes in the ram pressure or bulk speed are
calculated in the governing equations with the assumption that all species flow with the
same speed. The indices i ∈ {cx, rel} are the speeds
needed for the charge exchange cross-section and corresponding relative speeds. With the
definitions from McNutt et al. (1998) we have to
solve the following type of integrals: 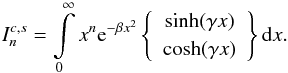 (B.1)The
following recursion holds:
(B.1)The
following recursion holds: 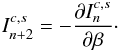 (B.2)Thus
we need only to know the four integrals (Gradstein
& Ryshik 1981), Nr. 3.562.3-3562.6:
(B.2)Thus
we need only to know the four integrals (Gradstein
& Ryshik 1981), Nr. 3.562.3-3562.6:
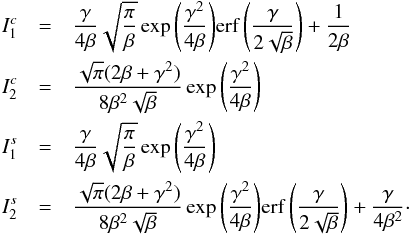 These
integrals need to be multiplied by the factors given in McNutt et al. (1998).
These
integrals need to be multiplied by the factors given in McNutt et al. (1998).
With these integrals it is easy to calculate the required speeds (for details see McNutt et al. 1998):
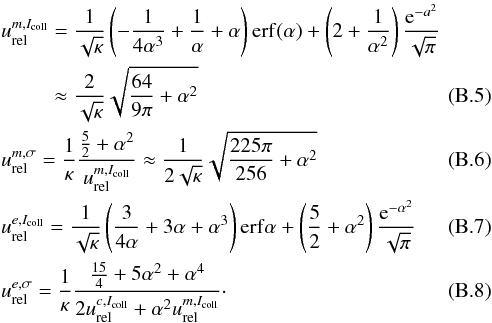 The
approximations in Eqs. (B.3) to (B.8) fit nicely, except for small errors
(see Fig. B.1). Note that the fit in Eq. (B.6) differs by a factor 0.5 from that of
McNutt et al. (1998).
The
approximations in Eqs. (B.3) to (B.8) fit nicely, except for small errors
(see Fig. B.1). Note that the fit in Eq. (B.6) differs by a factor 0.5 from that of
McNutt et al. (1998).
 |
Fig. B.1
Relative errors |
| Open with DEXTER | |
With the help of the integrals  it is
easy to calculate the higher-order correction terms. However, this is not necessary for
the p + H reaction, because
the second-order derivatives of the cross-sections, as shown in Fig. B.1, are orders of magnitudes lower than the
cross-section. Shown in Fig. B.2 are the functional
dependencies given by Fite et al. (1962) and by
Lindsay & Stebbings (2005), that is
it is
easy to calculate the higher-order correction terms. However, this is not necessary for
the p + H reaction, because
the second-order derivatives of the cross-sections, as shown in Fig. B.1, are orders of magnitudes lower than the
cross-section. Shown in Fig. B.2 are the functional
dependencies given by Fite et al. (1962) and by
Lindsay & Stebbings (2005), that is
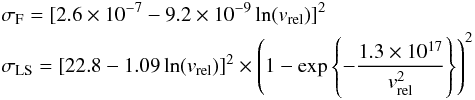 (B.9)where
vrel is given in cm/s and the
σ in
cm2.
(B.9)where
vrel is given in cm/s and the
σ in
cm2.
With the help of the computer algebra system wxMaxima3 it is easy to calculate the second derivatives of these commonly used
cross-sections for the p + H
reaction and the integrals for the second-order terms of the Taylor-expansion for
σcx. For the terms needed in the
continuity equation, we have to compare 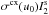 with the
second-order terms
with the
second-order terms 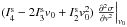 ,
where we neglected common factors for simplicity. In our notation
,
where we neglected common factors for simplicity. In our notation
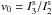 . With some
algebra, we find that
. With some
algebra, we find that 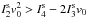 and thus finally
and thus finally
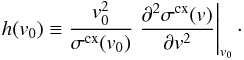 (B.10)The
function h(v) defined above is small for
all v, so
that we can assume that the higher-order terms in the Taylor expansion of
σcx vanish. In Fig. B.2 the function is shown for the two cross-sections.
(B.10)The
function h(v) defined above is small for
all v, so
that we can assume that the higher-order terms in the Taylor expansion of
σcx vanish. In Fig. B.2 the function is shown for the two cross-sections.
 |
Fig. B.2
Ratio h(v) (Eq. (B.10)) of the second-order integrated Taylor-expansion to the zeroth order for the two H-p charge exchange cross-sections discussed by Fite et al. (1962) and Lindsay & Stebbings (2005). The bump between the two downward spikes in the Lindsay-Stebbings curve is negative, but to represent it in a logarithmic scale, its absolute value was taken. See text for restrictions of the fit functions. |
| Open with DEXTER | |
It can be seen in Fig. B.2 that for the Fite et al. (1962) cross-section the second-order terms are nearly a factor 10 lower than the zeroth-order term for all speeds. For the Lindsay & Stebbings (2005) cross-sections this holds only for speeds lower than 4 × 107 cm/s = 400 km s-1. Around these speeds, that is, a commonly used solar wind speed, the second-order corrections are on the same order than the zeroth-order term.
Gains and losses from the original populations.
In the latter case, that is, if the higher-order terms cannot be neglected, in the analytic representation this will lead to clumsy formulas, which also need some computational time. Thus, it might be better to solve the collision integrals numerically.
Note, that for the hydrogen-proton reactions the fit function discussed in Fite et al. (1962) has an upper boundary of 10 keV, which corresponds to a relative speed of ≈1400 km s-1. The range in which the data were fitted by Lindsay & Stebbings (2005) has an upper boundary of 300 keV, which corresponds to a speed lower than ≈7500 km s-1. The data presented in Fig. 2 were taken from the Redbooks4 and reach to 63 keV, corresponding to ≈3400 km s-1. Some of the helium reactions have their maximum cross-section at higher energies, as can be seen in Table C.1, and their upper limits in energy/amu are higher than shown in Fig. 2.
All the fits given for the data from the Redbooks or the Aladdin database are mainly based upon a fit with Chebyshev polynomials. These polynomial fits are only good in the range given by the corresponding upper and lower (energy) boundaries and cannot be extended beyond these. Because usually it cannot be guaranteed in a large-scale model that the relative speeds are always in that range, a better fit function is needed, which can be extended beyond the boundaries, keeping in mind not to violate quantum mechanical requirements.
We here only discussed the simplest case, that is, the collision terms for the continuity equation. Of course this analysis must be performed not only for the remaining set of MHD equations, but has, especially, to be verified for all interactions.
Appendix C: Interaction terms
Gains from the new populations.
In the following we provide an overview of possible ionization reactions. In Table C.1, the first column gives the interaction term in the continuity equation, indicating the particle species: Xn with X∈ {H,He}, while n ∈ { 0,1,2 } gives the ionization state (usually the index 0 is omitted). Newly created ions are named as PUIXn and energetic atoms by ENAX. The reaction rates have the indices {cx, ei, pi} for charge exchange, electron impact, and photoionization, respectively. The rates are also denoted by ν(i,j), where i describes different reactants, while j stands for different products of the same reaction i. The tuple (i,j) is given in the fourth column, where a minus sign stands for losses and a plus sign for gains. To derive the total gains and losses one has to sum over all { i,j }. In the fifth and sixth column the maximal cross-section and its corresponding relative speed is given, respectively. In the third column the first reactant is a particle from the solar wind, while the second reactant is from the interstellar medium. This distinction is necessary to ensure correct sorting.
Note that in the charge exchange rate νcx = ρXσcxvrel the density of the first reactant is included and is indicated in the table by νcx,X.
Table C.1 contains the losses, Table C.2 the gains. In Table C.1 the approximate highest values for the cross-section are listed. They may vary by a factor of three and only indicate the correct order of magnitude. If a range is given for the corresponding relative velocity, the cross-section is a flat curve in that range.
All reactions that have a charged particle as the second reactant cannot flow in from the interstellar medium. Because the heliopause is a contact discontinuity that separates the solar wind and interstellar medium plasma, there is no flow of charged particles across the heliopause. Thus in Tables C.1 and C.2 the reactions labeled (3,1), (4,1), (5,1), (6,1), (8,1), (10,1), and (12,1) can be neglected.
The reactions labeled with an asterisk are sorted in pickup channels, even though they do not create new PUIs. For example, the reaction He+++H→He++H+ produces a new pickup hydrogen, but the change from doubly to singly charged helium does not change its character, that is He+ has the same bulk speed as He2+. Only the charge is changed, thus the new He+ does not
affect the dynamics (the H+ does). Nevertheless, these processes can have an effect on magnetic field turbulence (e.g. Shalchi et al. 2012). This aspect is interesting in the description of the diffusion tensor to model cosmic rays (Effenberger et al. 2012). The role of these types of processes for the turbulence will also be considered in future work.
From these tables the interaction terms for the governing equations can be determined.
For the neutral equation it is just the sum of all
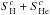 interaction
terms. More care must be taken for the ion governing equation, because the pickup terms
can cancel some of the ion terms, for example, the reaction H+ + H → H + H+ looses an original fast solar
wind proton, but gains a slow interstellar hydrogen atom, which does not change the
total ion mass.
interaction
terms. More care must be taken for the ion governing equation, because the pickup terms
can cancel some of the ion terms, for example, the reaction H+ + H → H + H+ looses an original fast solar
wind proton, but gains a slow interstellar hydrogen atom, which does not change the
total ion mass.
To describe the interaction terms for the momentum and energy equation, similar tables can now easily be constructed and the governing equations determined.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.