| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 43 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322254 | |
| Published online | 17 December 2013 | |
Online material
Selected YSOs and observing log.
Spectral types, extinction, and physical parameters.
Accretion properties of Lupus YSOs.
Results of the Lacc – Lline linear fits.
Appendix A: Correction for telluric bands
 |
Fig. A.1
Example of telluric-corrected spectrum (black lines) of the YSO Lup713 in the range of the K i λλ 766.49, 769.90 nm (upper panel) and the Na i λλ 818.33, 819.48 nm (lower panel) doublets. The uncorrected spectra are overlaid with red lines. |
| Open with DEXTER | |
The flux-calibrated one-dimensional spectra resulting from the X-shooter pipeline or our MIDAS procedure are not corrected for the contribution of telluric bands. Therefore, the telluric standards were used to perform the correction using the IRAF task “telluric”. The procedure basically consists of dividing the target spectrum by the telluric spectrum multiplied by an appropriate scaling factor. This factor depends on the ratio of the airmass of the target and the telluric standard. Since the targets and their assigned telluric standards were observed at very similar airmasses in most cases, this factor is typically close to one. The procedure was applied independently in the VIS and NIR spectra, in a different way.
Appendix A.1: Telluric correction in the VIS spectra
The correction was made directly on the one-dimensional flux-calibrated VIS spectra of the targets using the assigned tellurics. However, to avoid introducing of the SED of the telluric on the flux-calibrated spectra, the tellurics were first normalised to their continuum and their hydrogen lines and other stellar lines were removed by fitting combinations of Gaussian, Lorentzian, and Voigt functions. The resulting normalised telluric spectra, free of photospheric lines, were then used as input in the IRAF task “telluric”. In Fig. A.1 examples of the telluric correction in the spectral range of the K i λλ 766.49, 769.90 nm and the Na iλλ 818.33, 819.481 nm doublets are shown.
Appendix A.2: Telluric correction in the NIR spectra
For the NIR spectra, a pseudo-response function was first derived by dividing the not flux-calibrated telluric by a black-body of the same effective temperature as the telluric. This pseudo-response function was also cleaned for photospheric lines in the same way as in the VIS. The resulting pseudo-response function, free of stellar lines and containing the telluric bands, was then used as input in the IRAF task “telluric”. Note that the target spectrum to be used as input of the IRAF task was the not flux-calibrated one-dimensional spectrum. In this way, the telluric correction and the correction for the response function were made simultaneously in the NIR. Although the shape of the resulting spectrum after this procedure is correct, the flux calibration is made only relative to the pseudo-response function. Therefore, a factor was applied to bring the NIR spectrum to the absolute flux scale. This factor was estimated using the not telluric-corrected, but flux-calibrated spectra resulting from the X-shooter pipeline and our MIDAS procedure. In Fig. A.2 examples of the telluric correction of the YSO Lup713 are shown in two spectral ranges of the NIR arm. Note that in the range 2000–2140 nm the pipeline yields a bump with respect to the telluric corrected spectrum. This defect in the latter was corrected for because the pseudo-response function contains this bump as well.
 |
Fig. A.2
Examples of the telluric-corrected spectrum of Lup713 in two spectral ranges of the NIR arm. The uncorrected spectra are overlaid with red lines in both panels. |
| Open with DEXTER | |
Appendix B: Impact of veiling on spectral typing and extinction
Appendix B.1: Veiling and spectral indices
Strong veiling may influence the spectral indices used to classify the M-type YSOs. To investigate the impact of veiling on the spectral indices, we proceeded as follows. A constant veiling was artificially added to the spectra of the class III templates in the spectral range between 740 nm and 860 nm, where the indices are computed. Then, the new indices and spectral type of the “veiled” spectrum were derived. The effect of veiling is to yield systematically earlier types, but in that spectral range the veiling is expected to be stronger than one to induce a difference of about one spectral subclass. As seen in Sect. 4.1.1, the strongest veiling, at ~710 nm, among the M-type YSOs is lower than 0.6 and corresponds to Sz 113. For this object we estimate that veiling would introduce an uncertainty of 0.4 subclass in spectral type. For the other YSOs the excess emission in the Paschen continuum is lower (see Table 3). For all the M-type YSOs veiling is estimated to influence the spectral type classification by less than 0.3 spectral subclasses.
Appendix B.2: Veiling and extinction
The effect of strong veiling is to make YSOs objects intrinsically bluer than the templates we used to derive extinction. Thus, our method may underestimate extinction if veiling is very strong. To investigate the extent of this, we proceeded as follows. The observed spectrum of a given YSO, FYSO(λ), is the sum of the flux of the object, F∗(λ), plus the flux of the continuum excess emission, Fcont(λ), extincted with an extinction law, Aλ/AV. Accordingly, the flux we observe is FYSO(λ) = (F∗(λ) + Fcont(λ)) × 10− 0.4 (Aλ/AV) AV. To obtain the extinction free of veiling effects, we must apply our methods, not to FYSO(λ), but to the de-veiled spectrum: 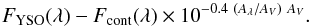 (B.1)
(B.1)
We can assume that the continuum flux is the model continuum excess emission derived in Sect. 4.1.1, hence from Eq. (B.1) we can compute a de-veiled spectrum, provided we know AV. Since we do not know AV in advance, we proceeded in a two-step fitting procedure. As first guess of AV we used the value derived from our template fitting procedure applied to FYSO(λ), and computed a de-veiled spectrum using Eq. (B.1). A new AV
was then derived from our fitting procedure applied to the first de-veiled spectrum. This spectrum was used to compute a new AV value and to redden the Fcont(λ) to be used again to calculate a second de-veiled spectrum, and so on until a AV value was found that leads to the best match with the template.
In practice, we used Sz 113 as a test case, the most strongly veiled M-Type YSO in our sample. The extinction we derived as first guess is 1 mag. Thus, the model continuum excess emission derived in Sect. 4.1.1 was reddened at extinctions between 1 mag and 2 mag in steps of 0.25 mag. The results were then subtracted from the observed spectrum of Sz 113. The several de-veiled spectra were then processed with our fitting procedure. The best compromise between reddened model continuum and de-reddened de-veiled spectra was found at AV = 1.5 mag. We conclude that for our most strongly veiled M-Type YSO extinction is underestimated by less than 0.5 mag.
Appendix C
Ancillary optical and NIR photometry.
Available photometric fluxes in milli Jy from 3.4 μm to 70.0 μm.
 |
Fig. C.1
Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
| Open with DEXTER | |
 |
Fig. C.2
Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
| Open with DEXTER | |
 |
Fig. C.3
Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
| Open with DEXTER | |
 |
Fig. C.4
Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
| Open with DEXTER | |
Extinction-corrected fluxes and equivalent widths of Balmer lines: Hα to Hϵ.
Extinction-corrected fluxes and equivalent widths of Balmer: H8 to H11.
Extinction-corrected fluxes and equivalent widths of Balmer lines: H12 to H15.
Extinction-corrected fluxes and equivalent widths of Paschen lines: Paβ to Pa8.
Extinction-corrected fluxes and equivalent widths of Pa9, Pa10, Brγ, and Br8.
Extinction-corrected fluxes and equivalent widths of helium lines.
Extinction-corrected fluxes and equivalent widths of helium lines.
Extinction-corrected fluxes and equivalent widths of Ca ii H and K and IRT lines.
Extinction-corrected fluxes and equivalent widths of the Na i D lines.
 |
Fig. C.5
Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. The Lupus YSOs are represented as black dots. The Hα, Hβ, and Hγ data available in literature for YSOs in Taurus (Herczeg & Hillenbrand 2008) and the σ-Ori cluster (Rigliaco et al. 2012) are overlaid as open circles and star symbols, respectively. |
| Open with DEXTER | |
 |
Fig. C.6
Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. The Lupus YSOs are represented as black dots. The H11 data available in literature for YSOs in Taurus (Herczeg & Hillenbrand 2008) and the σ-Ori cluster (Rigliaco et al. 2012) are overlaid as open circles and star symbols, respectively. |
| Open with DEXTER | |
 |
Fig. C.7
Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. The Lupus YSOs are represented as black dots. The Paβ, Paγ, and Brγ data available in literature for YSOs in Taurus (Muzerolle et al. 1998; Calvet et al. 2000, 2004), ρ-Oph and Chamaeleon (Natta et al. 2004), and the σ-Ori cluster (Rigliaco et al. 2012) are overlaid as open circles, ×-symbols, and star symbols, respectively. |
| Open with DEXTER | |
 |
Fig. C.8
Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. The Lupus YSOs are represented as black dots. The He i (λ5016 Å), He i (λ5876 Å), and He i (λ7065 Å) data available in literature for YSOs in Taurus (Herczeg & Hillenbrand 2008), the σ-Ori cluster (Rigliaco et al. 2012), and the Cha-II cloud (Biazzo et al. 2012) are overlaid as small open circles, star symbols, and as open circles, respectively. |
| Open with DEXTER | |
 |
Fig. C.9
Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. The Lupus YSOs are represented as black dots. The He ii (λ4685 Å) and Ca ii K data available in literature for YSOs in Taurus (Herczeg & Hillenbrand 2008) are overlaid as open circles. |
| Open with DEXTER | |
 |
Fig. C.10
Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. The Lupus YSOs are represented as black dots. |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


