| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321901 | |
| Published online | 03 September 2013 | |
Online material
Appendix A: Tracking a rotating starspot with respect to the transit chord
The geometry of the system is shown in Fig. A.1.
We started by considering a right-handed reference frame S, whose
origin coincides with the centre of the star. In this frame, the stellar rotation vector
defines the + z-direction, while the y-axis lies in
the plane of the sky. If we set the stellar radius to unity, the coordinates of a
starspot with latitude δ in this reference frame are simply 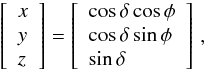 where φ = 2πt/Prot + φ0, Prot is the star’s rotational period, and φ0 is the longitude of the spot at some arbitrary time t = 0.
where φ = 2πt/Prot + φ0, Prot is the star’s rotational period, and φ0 is the longitude of the spot at some arbitrary time t = 0.
We defined a second right-handed reference frame S′ that shares the same origin and y-axis as frame S (i.e., y′ ≡ y), but whose x′-axis is pointing towards the observer. The stellar inclination i⋆ is the angle between the stellar rotation axis and the line-of-sight, i.e., the angle in the x′z′-plane between the z-axis of frame S and the x′-axis of frame S′. Coordinates in
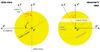 |
Fig. A.1 System geometry seen from the side (left) and from the observer’s standpoint (right), illustrating the two rotations needed to convert from frame S to frame S′′ (see text for details). |
| Open with DEXTER | |
frame S are transformed to frame S′ by performing a rotation by −(π/2 − i⋆) about the y-axis (or, equivalently, around the y′-axis; see Fig. A.1, left panel). This process is described in more detail in Appendix A of Aigrain et al. (2012).
We then considered a third right-handed reference frame S′′ that shares the same origin as S and S′, and the same x-axis as frame S′ (i.e., x′′ ≡ x′), but has its y′′-axis parallel to the transit chord. The sky-projected spin-orbit angle λ is defined as the angle in the plane of the sky between the projections of the orbital angular momentum and of the stellar spin axis, i.e., the angle in the y′′z′′-plane between the z′′-axis of frame S′′ and the z′-axis of frame S′. Coordinates in frame S′ are transformed to frame S′′ by performing a second rotation by −λ about the x′-axis (or, equivalently, around the x′′-axis; see Fig. A.1, right panel). The coordinates of the spot in frame S′′ are thus
 If
we observe the system for an infinite amount of time, a given spot that remains static
relative to the rotating surface of the star will eventually be crossed by the planet
during a transit, if, and only if,
If
we observe the system for an infinite amount of time, a given spot that remains static
relative to the rotating surface of the star will eventually be crossed by the planet
during a transit, if, and only if, 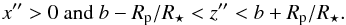 The
absence of spot crossings therefore excludes a specific volume in (i⋆,λ,δ)-space that we
explored by following the variations of x′′ and z′′ as φ varies. In the present study,
this was done by stepping through a grid of values, ranging from 0 to 180° for i⋆ and λ, and from 0 to
90° for δ, with 2° steps. At each point of the grid, x′′ and z′′ were evaluated
over a grid of φ-values, ranging from 0 to 360° with 2° steps. If the
conditions above (evaluated using the values for b and Rp/R⋆
given in Table 3, i.e., 0.341 and 0.09924,
respectively) were met for any value of φ, the corresponding cell in
the (i⋆,λ,δ) grid was
considered excluded.
The
absence of spot crossings therefore excludes a specific volume in (i⋆,λ,δ)-space that we
explored by following the variations of x′′ and z′′ as φ varies. In the present study,
this was done by stepping through a grid of values, ranging from 0 to 180° for i⋆ and λ, and from 0 to
90° for δ, with 2° steps. At each point of the grid, x′′ and z′′ were evaluated
over a grid of φ-values, ranging from 0 to 360° with 2° steps. If the
conditions above (evaluated using the values for b and Rp/R⋆
given in Table 3, i.e., 0.341 and 0.09924,
respectively) were met for any value of φ, the corresponding cell in
the (i⋆,λ,δ) grid was
considered excluded.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


