| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321400 | |
| Published online | 04 September 2013 | |
Online material
Appendix A: Determination of the flux ratios
Appendix A.1: Basics
Let
Fk, k = 1,2
be the line fluxes of the two components of the binary and
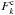 the
corresponding continuum fluxes. The observed composite spectrum normalised to the
common continuum of all components is
the
corresponding continuum fluxes. The observed composite spectrum normalised to the
common continuum of all components is 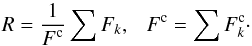 (A.1)KOREL delivers the
decomposed spectra normalised to the common continuum of the composite input spectrum,
(A.1)KOREL delivers the
decomposed spectra normalised to the common continuum of the composite input spectrum,
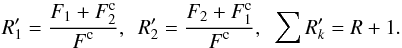 (A.2)The
wavelength-dependent ratios of the single continuum fluxes to the total flux are
(A.2)The
wavelength-dependent ratios of the single continuum fluxes to the total flux are
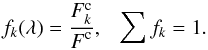 (A.3)We want to calculate
the decomposed spectra normalised to the continua of the single components,
(A.3)We want to calculate
the decomposed spectra normalised to the continua of the single components,
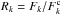 . Introducing
the line depths,
. Introducing
the line depths, 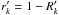 and
rk = 1 −Rk,
we simply get
and
rk = 1 −Rk,
we simply get 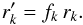 (A.4)For the
comparison with the synthetic spectra,
Sk, we replace the
rk in Eq. (A.4) by
sk = 1 −Sk.
As a measure of the goodness of fit, we use
(A.4)For the
comparison with the synthetic spectra,
Sk, we replace the
rk in Eq. (A.4) by
sk = 1 −Sk.
As a measure of the goodness of fit, we use  (A.5)where
the
(A.5)where
the 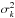 stand for
the accuracy of the line depths in the decomposed spectra. Since we compare the
spectra on the scale of the non-normalised decomposed ones, it will be
σ1 = σ2. Setting
f1 = 1 −f2 and derivating
Eq. (A.5) with respect to
f2, we finally get
stand for
the accuracy of the line depths in the decomposed spectra. Since we compare the
spectra on the scale of the non-normalised decomposed ones, it will be
σ1 = σ2. Setting
f1 = 1 −f2 and derivating
Eq. (A.5) with respect to
f2, we finally get 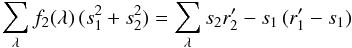 (A.6)from
which we can determine the optimum value of f2 (usually by
developing f2 into a polynomial of low degree in
λ and solving the resulting system of linear equations).
(A.6)from
which we can determine the optimum value of f2 (usually by
developing f2 into a polynomial of low degree in
λ and solving the resulting system of linear equations).
Appendix A.2: The optimum, continuum corrected solution
During the spectrum reduction, the observed composite spectrum is not exactly
normalised to the real local continuum but to some pseudo-continuum. We introduce
correction factors αk(λ)
in the sense 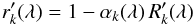 (A.7)where
(A.7)where
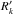 are the
wrongly normalised decomposed spectra. The
αk can be determined from spline fits
are the
wrongly normalised decomposed spectra. The
αk can be determined from spline fits
 to the
uppermost points in the decomposed spectra
to the
uppermost points in the decomposed spectra 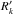 and
and
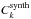 to those in
the synthetic spectra Sk. To compute the
pseudo-continua on the scale of the non-normalised decomposed spectra, the latter
spline fit has to be rescaled according to Eq. (A.4) and we get
to those in
the synthetic spectra Sk. To compute the
pseudo-continua on the scale of the non-normalised decomposed spectra, the latter
spline fit has to be rescaled according to Eq. (A.4) and we get 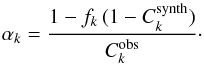 (A.8)
(A.8)
The occurrence of the so far unknown fk
in Eq. (A.8) does not complicate the
calculations because the continuum correction can be included into Eq. (A.5) to solve for the optimum values:
inserting the continuum-corrected 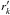 into Eq. (A.5) and derivating with respect to
f2 gives
into Eq. (A.5) and derivating with respect to
f2 gives 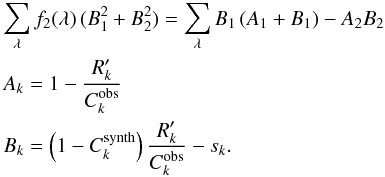 (A.9)After
solving Eq. (A.9) for
f2, χ2 is calculated from
Eq. (A.5). This can be done on a grid
of synthetic spectra sk to find the
minimum in χ2 and the corresponding optimum atmospheric
parameters. The renormalised decomposed spectra follow from Eqs. (A.4) and (A.7) to
(A.9)After
solving Eq. (A.9) for
f2, χ2 is calculated from
Eq. (A.5). This can be done on a grid
of synthetic spectra sk to find the
minimum in χ2 and the corresponding optimum atmospheric
parameters. The renormalised decomposed spectra follow from Eqs. (A.4) and (A.7) to 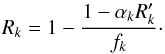 (A.10)
(A.10)
Appendix B: The Roche model
The Roche model is valid for centrally condensed stars where the gravitational
potential can be considered as the potential of point masses and, in the standard case,
for stars that rotate synchronously with the orbit and with rotation axes
perpendicularly aligned to the orbital plane. For reference, we give here the expression
for the Roche potential in the reference frame co-rotating with star 1 for the more
general case that star 1 rotates non-synchronously (see e.g. Bisikalo et al. 1999): 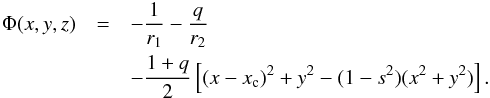 (B.1)All
coordinates have their origin in the centre of star 1 and are in units of the separation
a between the two stars. x points to star 2,
z along the rotation axis of star 1, and y lies in
the orbital plane to span a right-handed coordinate system.
q = M2/M1
is the mass ratio,
(B.1)All
coordinates have their origin in the centre of star 1 and are in units of the separation
a between the two stars. x points to star 2,
z along the rotation axis of star 1, and y lies in
the orbital plane to span a right-handed coordinate system.
q = M2/M1
is the mass ratio, 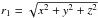 the distance to the centre of star 1,
the distance to the centre of star 1, 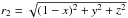 the distance to star 2, and
xc = q/(1 +q).
The synchronisation factor is
s = Ωrot/Ωorb.
the distance to star 2, and
xc = q/(1 +q).
The synchronisation factor is
s = Ωrot/Ωorb.
The Roche potential given by Eq. (B.1),
multiplied by −1, can be written as 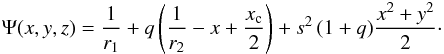 (B.2)The
shapes of the stars follow from the equipotential surfaces passing through the
substellar surface points P:
(B.2)The
shapes of the stars follow from the equipotential surfaces passing through the
substellar surface points P: 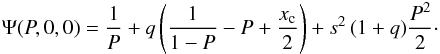 (B.3)The
position of the inner Lagrangian point L1 is calculated from
setting the derivative
dΨ(x,0,0)/dx to
zero and solving
(B.3)The
position of the inner Lagrangian point L1 is calculated from
setting the derivative
dΨ(x,0,0)/dx to
zero and solving 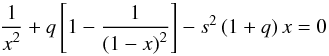 (B.4)numerically. The
radius rs that describes a sphere of the
same volume as the critical Roche lobe (the surface of the Roche potential through
L1) can be approximated with an accuracy of 1 %
(Eggleton 1983) by
(B.4)numerically. The
radius rs that describes a sphere of the
same volume as the critical Roche lobe (the surface of the Roche potential through
L1) can be approximated with an accuracy of 1 %
(Eggleton 1983) by
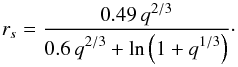 (B.5)
(B.5)
For a synchronously rotating star, this radius can be used to check if the star fills its critical Roche lobe or not. Instead, we used the filling factor f = P2/L1 as the more accurate criterion, where P2 is the substellar surface point of the secondary component (see Fig. 15). It is f = 1 when the star fills its critical Roche lobe, i.e. when P2 reaches the Lagrangian point L1.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


