| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321400 | |
| Published online | 04 September 2013 | |
Physical properties of the eclipsing δ Scuti star KIC 10661783⋆,⋆⋆,⋆⋆⋆
1
Thüringer Landessternwarte Tautenburg,
07778
Tautenburg,
Germany
e-mail: lehm@tls-tautenburg.de
2
Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK
e-mail: astro.js@keele.ac.uk
3
Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D,
3001
Leuven,
Belgium
e-mail: andrew@ster.kuleuven.be
4
Department of Physics, University of Zagreb,
Bijenicka cesta 32,
10000
Zagreb,
Croatia
e-mail: pavlovski@phy.hr
Received:
4
March
2013
Accepted:
15
July
2013
Context. KIC 10661783 is an eclipsing binary that shows δ Scuti-like oscillations. More than 60 pulsation frequencies have been detected in its light curve as observed by the Kepler satellite.
Aims. We want to determine the fundamental stellar and system parameters of the eclipsing binary as a precondition for asteroseismic modelling of the pulsating component and to establish whether the star is a semi-detached Algol-type system.
Methods. We measured the radial velocities of both components from new high-resolution spectra using TODCOR and compute the orbit using PHOEBE. We used the KOREL program to decompose the observed spectra into its components, and analysed the decomposed spectra to determine the atmospheric parameters. For this, we developed a new computer program for the normalisation of the KOREL output spectra. Fundamental stellar parameters are determined by combining the spectroscopic results with those from the analysis of the Kepler light curve.
Results. We obtain Teff, log g, vsini, and the absolute masses and radii of the components, together with their flux ratio and separation. Whereas the secondary star rotates synchronously with the orbital motion, the primary star rotates subsynchronously by a factor of 0.75. The newly determined mass ratio of 0.0911 is higher than previously thought and means a detached configuration is required to fit the light curve.
Conclusions. With its low orbital period and very low mass ratio, the system shows characteristics of the R CMa-type stars but differs from this group by being detached. Its current state is assumed to be that of a detached post-Algol binary system with a pulsating primary component.
Key words: asteroseismology / binaries: eclipsing / stars: variables:δScuti / stars: fundamental parameters / stars: abundances
Based on observations made with the 2-m Alfred Jensch telescope at the Thüringer Landessternwarte (TLS) Tautenburg and with the Mercator telescope, operated on La Palma by the Flemish Community at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.
Appendices are available in electronic form at http://www.aanda.org
The reduced spectra from the Tautenburg observatory are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/557/A79
© ESO, 2013
1. Introduction
The Kepler satellite delivered light curves (LCs) of thousands of pulsating stars and opened, with its unprecedented photometric accuracy and long sequences of continuous observations, a new window for asteroseismology. An asteroseismic modelling analysis requires accurate fundamental parameters of the stars that cannot be gathered from the single-band photometry of Kepler alone. Ground-based, multi-colour, or spectroscopic follow-up observations can provide this missing information.
Eclipsing binaries (EBs) are outstanding targets for determining the fundamental parameters of stars from a combined LC and spectroscopic analysis. KIC 10661783 is a short-period binary star that was found to be an EB by Pojmanski (1997). It was chosen by Southworth et al. (2011, hereafter Paper I) as a target for detecting of pulsations in the component stars of EBs, and Kepler observations of both long and short cadence were obtained. These observations were augmented with SuperWASP photometry in order to precisely measure the orbital period of the system. The residual LC after subtracting the eclipse variability was subjected to a frequency analysis, revealing at least 68 frequencies of which 55 can be attributed to pulsation modes. The main frequency range lies between 18 and 31 d-1, and the variability due to pulsations could be assigned to the primary component of the system.
In their modelling of the Kepler LC, the authors were able to define two possible solutions: that of a detached EB with a mass ratio of q = 0.25 and that of a semi-detached EB (secondary star filling its Roche lobe) with q = 0.0626. The latter option was preferred in light of preliminary spectroscopic measurements that favoured a low mass ratio. This implied that KIC 10661783 was a member of the class of “oEA” stars (Mkrtichian et al. 2002, 2003): active Algol-type systems where the primary component shows δ Scuti-type pulsations. Moreover, it would be the oEA star with by far the richest pulsation spectrum detected until now. In the absence of radial velocity measurements, they were unable to measure the physical properties of the two stars.
The analysis of the Kepler LC of this short-period (P = 1.2313622 d) EB, after removing the pulsation signatures, encountered some problems. A reasonable fit to the data could only be obtained by assuming a higher albedo for the primary than physically expected and an unusually low mass ratio of q = 0.0626. Together with the short period, these properties would make KIC 10661783 a member of the subgroup of R CMa stars among the Algol-type stars (see Varricatt & Ashok 1999 for a discussion; Budding & Butland 2011 for R CMa). The mass ratio is a critical piece of information when assessing wether the secondary component fills its critical Roche lobe (RL) or not, i.e. if the system is semi-detached or detached. It was derived in Paper I from the LC alone, and thus depended on the reliability of the model fit to the data.
In this paper we obtain and analyse new spectroscopic observations, which we use to improve the photometric model and to directly determine the absolute masses and radii of the components. We investigate the hypothesis that KIC 10661783 is a semi-detached system, and determine the effective temperatures and chemical abundances of the stars from analysis of the separated spectra of the components.
2. Observations
Number N of spectra obtained in different nights in 2010.
In 2010, we obtained 26 high-resolution spectra of KIC 10661783 in seven almost consecutive nights using the Coudé-échelle spectrograph at the 2-m telescope of the Thüringer Landessternwarte (TLS) Tautenburg, Germany, and 59 spectra in 11 consecutive nights with the HERMES spectrograph (Raskin et al. 2011) at the 1.25-m Mercator telescope at La Palma, Spain. Table 1 gives the journal of observations.
The TLS spectra have a resolving power of 64 000 and cover the wavelength range 4700–7400 Å. The exposure time was 30 min and the spectra have a signal-to-noise ratio (S/N) of 90 on average. The HERMES spectra have a resolving power of 85 000 and cover 3740−9000 Å. The exposure time was 40 min and the mean S/N was 130. The higher S/N obtained with the HERMES spectrograph is due to its higher efficiency and the better weather and seeing conditions at La Palma.
The TLS spectra were reduced using standard MIDAS packages and a routine for the calibration of the instrumental radial velocity (RV) zero-point using O2 telluric lines. The idea of using telluric absorption lines for obtaining accurate RV measurements was proposed by Griffin (1973). Figueira et al. (2010, 2012) showed, based on a study done for the HARPS spectrograph at La Silla, that O2 telluric lines are stable down to 10 m s-1 on a timescale of 6 years and that atmospheric phenomena introduce variations at the 1−10 m s-1 level (rms). One complication is that the telluric bands cover only certain regions of the observed spectra. From our experience with the TLS spectrograph over several years, we can reach an accuracy of better than 50 m s-1 in this way. For the reduction of the HERMES spectra we used the HERMES reduction pipeline, followed by the normalisation of the spectra to the local continuum based on a separate routine.
3. Investigation of the primary component
Throughout the paper, we designate the brighter component of KIC 10661783 (the former mass-gainer according to the standard evolutionary scenario for Algol systems) as the primary star and the low-mass companion (the donor) as the secondary star.
3.1. Radial velocities and atmospheric parameters
In this first approach, we ignored the faint contribution of the secondary component to the composite spectra. RVs were measured from the composite spectra by cross-correlation in two steps. In the first step, we determined the RVs to build a mean spectrum from the observed ones. We started with one arbitrary spectrum of reasonably high S/N as the template and determined the RVs on a relative scale. Then we shifted all the observed spectra according to the measured RVs, co-added them and repeated the RV measurement using the averaged, mean spectrum as the template. After an iteration, we fitted the averaged spectrum by synthetic spectra calculated on a grid of atmospheric parameters and determined the RVs from cross-correlation of the observed spectra with the best-fitting synthetic spectrum on an absolute scale. The synthetic spectra were calculated with SynthV (Tsymbal 1996) based on model atmospheres computed with LLmodels (Shulyak et al. 2004). The line tables were taken from the VALD data base (Kupka et al. 2000). The fitting procedure was described in detail in Lehmann et al. (2011). Finally, we repeated the procedure with the new, synthetic template, iteratively improving the RVs as well as the mean spectrum of KIC 10661783.
Atmospheric parameters derived from the mean composite spectrum of KIC 10661783.
From the final mean spectrum, we determined the atmospheric parameters listed in Table 2. Although these results have been derived from the composite spectrum of the binary, they are good first estimates of the stellar parameters of the primary star because the secondary star contributes only a small fraction of the light in the spectrum (see Sect. 4).
3.2. Orbital solution
We used the method of differential corrections to the orbital elements (Schlesinger 1910; Sterne 1941) to determine the orbit of the primary component from the observed composite spectra. After deriving the solution from the complete data set, we fixed the obtained parameters and calculated the O−C residuals for the TLS and HERMES RVs separately. The difference between the two data sets is 1.615 km s-1 and we added this value to the HERMES RVs to calculate the final orbital solutions. Including all the RVs and allowing for an eccentric orbit, we obtain an eccentricity of e = 0.036 ± 0.001 from all RVs and 0.016 ± 0.006 if we omit the RVs around primary eclipse. No significant non-circularity could be found after also rejecting all spectra near to the secondary eclipse. From now on we assume a circular orbit for this close binary system and fix the orbital period to the value of 1.23136220 d obtained in Paper I. This value is two orders of magnitude more precise than that which can be determined from our spectroscopic observations. Figure 1 shows the RVs folded with the orbital period. In the O-C residuals (Fig. 2) we clearly see the Rossiter-McLaughlin effect (Rossiter 1924; McLaughlin 1924) around Min I. This will be discussed in Sect. 4.4, based on the analysis of the individual components. The resulting orbital parameters are listed in Table 5 given in Sect. 4.5 and will be discussed there. The quoted errorbars are formal 1σ limits computed from the inverse matrix of the least squares problem of the differential-correction approach.
We used the period04 program (Lenz & Breger 2004)) to search the O-C residuals of the spectroscopic orbital solution for periodic variations. No significant contributions could be found up to the Nyquist frequency of 8.37 c d-1.
 |
Fig. 1 RVs of the primary component measured from TLS (squares) and HERMES (crosses) spectra folded with the orbital period. The solid curve is based on the parameters listed in Table 5. Phase zero corresponds to Min I. |
 |
Fig. 2 O−C residuals of the fit in Fig. 1, indicating the presence of the Rossiter-McLaughlin effect during primary eclipse. |
4. Investigation of both components
4.1. The impact of the secondary star
For a visual search for the lines of the secondary, we arranged all spectra in a two-dimensional frame (Fig. 3), averaging them into 30 orbital phase bins. The impact of the secondary star could be only detected in a few iron lines. It is most prominent (although still very faint) in the Fe ii 4957 Å line. Figure 3 shows this line where the central line depth is about 13 secondary could only be found in the HERMES spectra, which have a higher S/N than the TLS spectra.
4.2. Decomposing the spectra with KOREL
We used the Fourier-based KOREL program (Hadrava 1995, 2006) to decompose the spectrum of KIC 10661783. It delivers the decomposed spectra normalised to the common continuum of the composite input spectrum, together with the optimised orbital elements. In the case of light variability like in EBs, one can also calculate variable line strengths (mean over all included lines) for both components separately.
 |
Fig. 3 Strong and faint Fe ii 4957 Å lines of the primary and secondary, respectively. The vertical axis gives the orbital phase of observation, and secondary eclipse occurs at the centre of the image. The elongation in RV (horizontal axis) corresponds to the velocity semiamplitudes given in Table 5. |
 |
Fig. 4 Decomposed spectra of the primary and secondary components. The latter is shifted upwards by 0.05 for clarity. |
Elemental abundances of the primary (A1) and the secondary (A2) compared to the Sun and their 1σ errors.
One problem in applying the KOREL program is that the zero frequency mode in the Fourier domain is unstable and cannot be determined from the Doppler shifts alone. This effect gives rise to low-frequency undulations in the continuum of the decomposed spectra and can prevent an accurate determination of the local continuum. We therefore followed the procedure discussed by Hensberge et al. (2008), which shows that inherent light variations can stabilise the separation of the stellar components in the KOREL method, and allowed for variable line strengths in the KOREL solutions. In this way, the degeneracy in the determination of the local continuum should be lifted by the variation of the light ratio. However, we were surprised by our first analysis, that resulted in two identical decomposed spectra. The calculated line strengths of both components were extraordinarily strong at some single epochs close to the eclipses and very weak over all other phases. We assume that most of the spectra were included with zero weight into the calculations. One reason that the variable weighting of spectra failed could be, besides the faintness of the second component, the strong Rossiter-McLaughlin effect during primary eclipse. It deforms the lines of the primary during the eclipse (see Sect. 4.4) which is not taken into account by KOREL.
In a second attempt, excluding the eclipse phases and using constant line strengths, we ended up with a reliable solution. We used the HERMES spectra only, starting with the iron line shown in Fig. 3, and expanded the wavelength range we used up to a limit where we obtained the smallest scatter of the RVs of both components. From this region, 4900–5193 Å, we calculated the orbital elements listed in Table 5 and used them as fixed parameters for the spectral disentangling that we performed on a wider spectral range. Because the continuum calculated during the normalisation of the observed spectra is very uncertain at the blue edge of the spectra, we restricted the wavelength range for the spectral disentangling to λ > 4000 Å.
As noted above, KOREL introduces undulations in the calculated continuum of the decomposed spectra. To overcome this problem, we split the spectra into overlapping wavelength bins of 50 Å width, with wider bins for the Balmer lines, and corrected the continuum of each of the resulting decomposed parts using spline functions. The final decomposed and corrected spectra were then built by merging all the short, decomposed regions and averaging the overlapping parts. It can be seen from Fig. 4 that the resulting spectra do not suffer from any continuum undulations.
One remaining problem is the low accuracy of the calculated continuum in the region of the broad Balmer lines of the primary, where we had to use larger wavelength regions for the disentangling. The problem is not as serious for the secondary component because the Balmer lines of the cooler star are much narrower. To check for the accuracy achieved, the CRES program1 (Ilijic 2004) was applied to decompose the Hβ and Hγ line profiles. CRES uses singular value decomposition in the wavelength domain to disentangle spectra. The agreement of the resulting profiles with those obtained with the KOREL program was excellent. This is illustrated by Fig. 5 which shows a comparison of the Hβ line profiles of the primary component obtained with both methods where the CRES decomposed spectrum looks less noisy because it was rebinned to a smaller resolution to save computing time.
 |
Fig. 5 Comparison of the decomposed Hβ line profiles of the primary component obtained with CRES (black) and with KOREL (red). |
4.3. Analysis of the decomposed spectra
For analysis of the decomposed spectra, we used the same approach as in Sect. 3.1 but extended our program by including the computation
of the wavelength-dependent flux ratio between the components, which is needed to
normalise the KOREL output spectra. A similar and more sophisticated method was described
in Pavlovski & Hensberge (2005). We used
the approach introduced by Lehmann & Tkachenko
(2012), which is described in detail in Appendix A. For the wavelength dependence
of the continuum flux ratio
f = F2/(F1 + F2),
we used the linear approach: 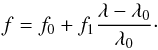 (1)In a first step,
we determined Teff, [M/H], and
vsini together with the flux ratio and continuum
corrections. Because of the observed ambiguity between log g and the
other parameters we fixed log g of the components to the values derived
from the combined LC and RV analysis after iteration (see Table 7 in Sect. 5). Then we
renormalised the decomposed spectra according to the derived flux ratio, applying the
continuum corrections as described in Appendix A, and analysed the renormalised spectra
separately. Starting with the abundances of all elements scaled to the derived
[M/H], we determined the optimised abundances of each element step
by step, including only those elements where significant contributions could be found in
the wavelength range under consideration. We did not try to adjust the helium abundance
because we do not observe any He lines in this region. For the cooler secondary star, we
included molecules in the spectral line tables and were therefore able to determine its
carbon abundance by fitting the CH bands.
(1)In a first step,
we determined Teff, [M/H], and
vsini together with the flux ratio and continuum
corrections. Because of the observed ambiguity between log g and the
other parameters we fixed log g of the components to the values derived
from the combined LC and RV analysis after iteration (see Table 7 in Sect. 5). Then we
renormalised the decomposed spectra according to the derived flux ratio, applying the
continuum corrections as described in Appendix A, and analysed the renormalised spectra
separately. Starting with the abundances of all elements scaled to the derived
[M/H], we determined the optimised abundances of each element step
by step, including only those elements where significant contributions could be found in
the wavelength range under consideration. We did not try to adjust the helium abundance
because we do not observe any He lines in this region. For the cooler secondary star, we
included molecules in the spectral line tables and were therefore able to determine its
carbon abundance by fitting the CH bands.
 |
Fig. 6 Chemical abundances of the primary (crosses) and the secondary (open circles) components, relative to solar. Chemical elements are sorted by their atomic numbers. The dashed and dotted lines show the weighted mean for the primary and secondary stars, respectively. |
Table 3 lists the determined abundances. The uncertainties were calculated from the hypersurface of the χ2 values of all grid points in Teff, vsini, and the abundance of the corresponding element (see Lehmann et al. 2011) and include possible correlations between these parameters.
Figure 6 shows the abundances with their 1σ error bars. The dashed and dotted lines show the weighted means calculated from all elements except for N for the primary and C for the secondary. It can be seen that the abundances of all other elements agree with the weighted mean to within 1σ. We conclude that N is strongly overabundant in the primary and C is underabundant in the secondary star.
Table 4 lists the derived atmospheric parameters where [Fe/H] is taken from Table 3 and [M/H] represents the mentioned weighted mean. In the lower part of Table 4, we list the coefficients of the flux ratio function as defined in Eq. (1).
Atmospheric parameters from spectrum analysis.
4.4. Orbital solution with TODCOR
The KOREL code determines the orbit directly from the observed composite spectra. The RVs calculated with KOREL are not independent measurements, but represent the shifts applied to the spectra. They are optimised together with the orbital elements assuming Keplerian motion. An additional aspect of the KOREL solution is that the spectra close to primary minimum had to be excluded from the calculations. We therefore used the TODCOR program (Mazeh & Zucker 1992, 1994; Zucker & Mazeh 1994) together with the HERMES spectra of KIC 10661783 to obtain independent measurements of the RVs of both components.
Orbital parameters of the binary system (see text).
We applied an implementation of TODCOR that is able to determine the RVs from composite spectra together with the flux ratio between the components. We used two synthetic template spectra, calculated for the Teff, log g, and vsini listed in Table 4. The resulting RVs of the primary were unsatisfactory, because we could not find any sign of the Rossiter-McLaughlin effect (RME), despite this being clearly discernable in the RVs that we obtained from cross-correlation (see Fig. 2).
Considering the RME, we must be aware that we are dealing with two different types of velocity. One type is the classical RV, defined as the velocity component of the centre of mass of the star along the line of sight. For binary stars this is due to Keplerian motion, and can easily be measured from cross-correlation or line profile fitting when the lines are symmetrically broadened by rotation. The symmetry is lifted during the eclipses and the observed spectrum results from the line profiles emerging from single surface points, each RV-shifted by rotation according to its position on the stellar disc, integrated over the visible, non-eclipsed part of this disc. What we call RV in this case strongly depends on how the positions of the resulting asymmetric lines are measured. Next, we wanted to estimate the expected amplitude of the RME for KIC 10661783, and the degree of asymmetry of the line profiles caused by the RME.
 |
Fig. 7 Rossiter-McLaughlin effect: synthetic line profiles computed for different phases around primary eclipse (left) and the RVs computed from these profiles (right). |
Ohta et al. (2005) developed analytical formulae to estimate the amplitude of the RME for transiting planets. These formulae are only valid for the case that the radius of the planet is much smaller than that of its host star. Instead, we used a simple model consisting of a rotating star eclipsed by a dark disc moving across the disc of the star at a latitude corresponding to the derived orbital inclination and separation of KIC 10661783 (see Table 7). We divided the stellar disc into 100 by 100 surface elements. For each of these elements we computed the emerging line profile assuming Gaussians for the intrinsic profiles, shifted in RV by rotation. The intensity was scaled according to a linear limb darkening law. All parameters (separation, inclination, radii, and vsini) were adjusted to our final measurements of these values (Tables 5 and 7). Figure 7 shows the profiles obtained from an integration across the visible, uneclipsed disc. We define the eclipse phase to be −0.5 at the beginning and +0.5 at the end of the eclipse. It can be seen that the impact of the RME on the line profiles causes a shift of the line centre (or centre of gravity) in wavelength (or RV) which is due to the varying shape of the profiles. The lines get highly asymmetric during ingress and egress and the star shows a double-peaked profile at the centre of the (partial) eclipse. The RVs shown in the right panel of Fig. 7 are computed from the centres of gravity of the profiles. Thus, we expect an amplitude in RV of the order of ± 10 km s-1 and a varying effective line width having minima during ingress and egress of primary eclipse and a maximum at its centre.
 |
Fig. 8 Flux ratio (top) and vsini of the primary component (bottom) determined with TODCOR, folded with the orbital period. Phase zero corresponds to Min I. |
 |
Fig. 9 RVs of the primary component determined with TODCOR. The solid curve shows the orbital solution calculated with PHOEBE. RVs included into the solution are shown by plus signs, outliers by crosses. The lower panel shows the O–C residuals. |
To account for the latter effect, we computed the RVs with TODCOR in a second step from each spectrum by using different vsini values for each component and optimising the vsini by maximising the correlation coefficient. The results are shown in Figs. 8 to 10. We used a grid of synthetic spectra with a 1 km s-1 step width in vsini. The optimum values for the primary component are shown in the lower panel of Fig. 8. Outside the primary eclipse we see a small scatter that increases around secondary minimum. The behaviour during primary minimum is exactly as expected and described above. The behaviour during secondary eclipse appears to be an artefact, due to line-blending effects between the two components and the fact that TODCOR searches for a second component even when the eclipse is total. For the computation of the RVs we have set the vsini of the primary star outside primary eclipse to the mean value of 74.5 km s-1. This value is slightly lower than the value of 79 ± 4 km s-1 obtained from the analysis of the decomposed spectra (Sect. 4.3). The vsini values of the secondary component obtained in this way show pure scatter of about ± 2 km s-1. For the final calculations, we fixed them to the mean value of 38 km s-1 that is distinctly lower than the value of 48 ± 3 km s-1 following from the spectral analysis. A discussion of this result is given in the next two sections.
Figure 8 shows, in its upper part, the flux ratio obtained versus orbital phase. Its value outside the eclipses is slightly lower than the value of 0.063 obtained from spectrum analysis (Sect. 4.3). It can be seen that the program recognises the increase of the flux ratio during primary eclipse and a decrease during secondary eclipse. For the computation of the RVs, we set the flux ratio for the central part of the secondary eclipse to zero since it is a total eclipse.
Figures 9 and 10 show the obtained RVs folded on the orbital period. Values very close to the systemic RV could not be determined accurately, due to blending effects. Such values occur at the centre of the primary eclipse for the RVs of the primary and during both eclipses for the secondary and have been rejected from the computation of the orbit. The RME during primary eclipse can clearly be seen, is of the right magnitude compared to Fig. 7, and is much more pronounced than in Fig. 1 where we neglected the impact of the secondary component on the spectra.
Finally, we used the PHOEBE program (Prša & Zwitter 2005) for computing the orbit based on the RVs derived with TODCOR. This program is able to include the RVs of both components into a common solution and also considers the RME and proximity effects. We used different weights for the RVs of the primary and secondary component. They were obtained from the final standard deviation of the corresponding O-C values, which are 0.75 km s-1 for the RVs of the primary and 3.13 km s-1 for those of the secondary. The orbital curves computed with PHOEBE are shown in Figs. 9 and 10. Table 5 lists the results, together with the results from our previously described methods and the combined solution described in Sect. 5. It lists the systemic velocity γ, the RV semiamplitudes of the components K1,2, the mass ratio q, the orbital separation a, and the inclination i derived with different methods. Orbital period and time of primary mid-minimum were fixed to the photometric values of 1.2313622 d and 245 506 5.77701, respectively. Values that were not directly measured but were derived are given in parentheses. The fitting of the RME with PHOEBE also allowed us to compute, based on the measured vsini, the values of orbital separation and inclination. The result is in good agreement with the orbital solution obtained from the LC analysis.
4.5. Comparison of the different solutions
The RVs determined via cross-correlation can only give the RV semi-amplitude, K1, of the primary component. Since we neglected the impact of the secondary on the composite spectra, the derived K1 will slightly differ from the true value. Thus, the results have been only used to obtain the mean composite spectrum for a first analysis.
The orbital solution determined with KOREL was derived by fitting the orbital parameters simultaneously with the optimum shifts (formal RVs). TODCOR also uses the composite spectra but determines the RVs of the single stars by cross-correlating the observed spectra with two different synthetic templates in a two-dimensional plane. The orbital elements derived with TODCOR show the smallest uncertainties. Whereas the uncertainties in K1 obtained from KOREL and TODCOR are of the same order, the KOREL uncertainty in K2 is an order of magnitude higher. We assume that the low accuracy of K2 derived with KOREL also influences the determination of K1 and adopt the orbital parameters that are based on the TODCOR RVs as the final ones.
We used TODCOR mainly to derive the RVs of the components. Using optimised line widths, TODCOR only fails to compute correct RVs for the primary star at the centre of primary minimum, where line blending effects between both components occur and the spectral lines of the primary component are deformed by the RME. Although we notice that the line widths and flux ratio during primary eclipse are adequate, we do not trust the absolute values delivered by TODCOR. Firstly, the flux ratio during primary eclipse is much too high compared to the eclipse depth (and should be zero during secondary eclipse). From the LC (Fig. 14) we expect an increase of the flux ratio by a factor of about 1.26, whereas TODCOR (Fig. 8) yields more than twice the flux ratio outside the eclipses. Secondly, the vsini derived from spectral analysis is more reliable because it exactly corresponds to the case of synchronised rotation.
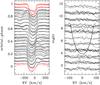 |
Fig. 11 Left: LSD profiles computed from all HERMES spectra, vertically arranged according to orbital phase. Profiles distorted by the RME are shown in red. Right: differential LSD spectra from different nights (see text). The synthetic LSD profile of the primary is overplotted for a better distinction between line profile and continuum regions. |
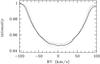 |
Fig. 12 Comparison of the LSD profile observed for the primary component (thick) with synthetic LSD profiles computed for vsini values of 75 (dotted), 80 (solid), and 85 km s-1 (dashed). |
 |
Fig. 13 Comparison of the LSD profile observed for the secondary component (thick) with synthetic LSD profiles computed for vsini values of 38 (dotted), 48 (solid), and 58 km s-1 (dashed). |
4.6. LSD profiles
To prove that the spectral disentangling delivered correct results and the vsini obtained from spectrum analysis give the accurate values, we analysed the observed instead of the decomposed spectra. To enhance the S/N, we applied the least squares deconvolution (LSD) technique (Donati et al. 1997; Donati & Collier Cameron 1997) to each of the observed spectra in the range 4910–5670 Å (a region redwards of Hβ with many metallic lines). LSD computes high-precision average line profiles from all lines in a spectrum, as shown in the left panel of Fig. 11. We selected 23 spectra taken at orbital phases of largest RV separation. The computed LSD profiles were shifted according to the orbital RVs of the primary and co-added to get the mean LSD profile of the primary component. The secondary was treated analogously. Figures 12 and 13 show the comparison of the observed mean profiles with synthetic LSD profiles computed from our atmospheric model (Table 2) for different vsini. It can be seen that the vsini of 79 km s-1 of the primary and 48 km s-1 of the secondary derived from the analysis of the decomposed spectra fit the observed profiles very well. In particular, we can rule out the vsini of 38 km s-1 corresponding to the mean value from TODCOR.
The right panel of Fig. 11 shows the differential spectra after subtracting the best-fitting synthetic LSD profile from the observed ones (profiles observed during primary minimum are removed). The vertical axis gives the number of the observing night in a running order. It can be seen that the scatter in the range of the line profiles is distinctly larger than in the continuum regions and it can be assumed that the differential spectra show intrinsic signals from high-degree l modes of non-radial pulsations. The investigation of this effect is beyond the scope of the current paper.
5. Combined photometric-spectroscopic analysis
In Paper I we found two good solutions to the LC, one with a detached configuration and a mass ratio of q = 0.25 and one with a semi-detached nature and q = 0.0626. We rejected the former on the basis of the spectroscopic evidence existing at the time which favoured the smaller q, finding therefore that KIC 10661783 was an Algol system. Now we have a reliable q from extensive spectroscopy it is apposite to revisit the LC analysis. The spectroscopic q = 0.09109 is indeed rather different from either choice considered in Paper I.
We modelled the Kepler short-cadence LC from Quarter 2.3, after removal of the pulsations. The data were converted to orbital phase and binned into 230 normal points. The bin sizes were chosen to be 0.002 phase units during eclipse and 0.02 outside eclipse, in order to adequately sample the eclipse shapes whilst limiting the computation time for individual solutions. This material is identical to that considered in Sect. 5 in Paper I, and the scatter of the data is dominated by imperfectly removed pulsations, not by Poisson noise. For the modelling process we adopted the 2004 version of the Wilson-Devinney (WD) code (Wilson & Devinney 1971; Wilson 1979), accessed via the jktwd wrapper (Paper I) and hereafter called wd2004.
Summary of the control and fixed parameters for the wd2004 solution.
Our immediate conclusion was that fixing q = 0.09109 destroys the quality of the fit under the assumption of a semi-detached configuration. This mass ratio causes the secondary star to be too large to match the data, and the rms of the residuals around the best fit changes from 0.4 mmag to 10 mmag. We therefore reconsidered the possibility that the system is actually detached, thus removing the requirement for the secondary star to fill its Roche lobe. This led to an acceptable fit to the LC, with parameters which are nevertheless very close to those found in Paper I.
Table 6 gives a summary of all control and fixed parameters. For our final solutions we used mode 2 in wd2004, which corresponds to a detached configuration with the light contributions of the two stars governed by their radii and Teffs. We fixed the Teff of star A to 7764 K as determined from spectral analysis and included the Teff of star B as a fitted parameter. The Kp passband is not implemented in wd2004, but this does not present a problem as we are studying single-band data. Solutions were calculated using the Johnson V, R and I and Cousins R and I passbands, allowing us to verify that this mismatch between passbands is unimportant. This also helped us to explore the intrinsic precision of the solution by comparing multiple alternatives with slightly different starting assumptions. The solutions for the V and R passbands yield Teffs for star B in very good agreement with the spectroscopic value found above.
Use of the detailed treatment of reflection in wd2004 had a negligible effect on the results. We nevertheless adopted the detailed treatment as it is physically more realistic. The mass ratio was fixed at 0.09109 and a circular orbit was assumed. The attempt to include the rotational parameters f1 and f2 as fitted parameters led to unphysical results. They were fixed to values of 0.756 and 1.039 as found below, where a value of 1.0 means the star is rotating synchronously with the orbital motion.
Limb darkening was incorporated using the square-root law; the linear limb darkening coefficient (LDC) for star A was fitted and the other three coefficients were fixed to values obtained from interpolation within the tables of van Hamme (1993). This approach was based on preliminary fits which showed that there is insufficient information in the LC to fit for the coefficients which we fixed, and on past experience which showed that the two coefficients for one star are highly correlated (e.g. Southworth et al. 2007). The other fitted parameters were the orbital inclination, the potentials of the two stars, and the passband-specific light from star A.
Summary of the fitted and derived parameters.
The values of the gravity darkening exponents do not have a significant effect on the geometric parameters of the fit so they were fixed to 1.0. The albedos were included as fitted parameters, and a large value for star A is required to fit the data. This situation was noted in Paper I and implies that wd2004 is slightly struggling to fit data of such high quality as we have here. The albedos are strongly correlated with the gravity darkening exponents; including the gravity darkening exponents as fitted parameters yields lower values for the albedos but unreasonable values for the gravity darkening exponents. We interpret this as a limitation of the radiative physics included in the wd2004 model.
The final results of the modelling process are given in Table 7. We have assigned an errorbar to each fitted parameter based on the variation of its value between the many acceptable solutions obtained throughout the modelling process. These errorbars are in all cases significantly larger than the formal errors returned by wd2004, which are based on the covariance matrix. Past experience shows that the formal errors are optimistic, at least in part because they neglect correlations between parameters (Paper I, Pavlovski et al. 2009; Tkachenko et al. 2012).
The vital results from this section are the conclusion that KIC 10661783 is a detached binary system, and the measurement of three photometric parameters from its LC. These three parameters are the orbital inclination and the fractional radii of the two stars (i.e. the absolute radii divided by the orbital semimajor axis). The best fit to the data is shown in Fig. 14.
The physical properties of the system follow from the spectroscopic and photometric quantities determined above. We have calculated the physical properties from the velocity semiamplitudes, effective temperatures and fractional radii of the two stars, and the orbital inclination of the system. This was done with the absdim code (Southworth et al. 2005) and using the set of physical constants tabulated by Southworth (2011). Uncertainties were propagated within this code by a perturbation approach.
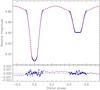 |
Fig. 14 Best fit of the phase-binned Kepler short-cadence data of KIC 10661783 using wd2004. The fitted data are shown in the upper part of the plot and the residuals in the lower part of the plot. |
6. The Roche geometry of the system
In Paper I it was suspected that KIC 10661783 is a semi-detached system and could be an oEA star. Using the newly determined mass ratio, we now find that its LC can be modelled in a satisfactory way only if we adopt a detached configuration. We now confirm this finding directly from the Roche model, and exclude signs of activity in the system by examining spectra taken at different orbital phases.
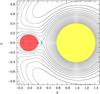 |
Fig. 15 Cut through the Roche equipotential surfaces in the x–y plane. The primary component is shown in yellow, the secondary in red colour. The plus sign marks the L1-point, the cross the P2-point. |
In the Roche model and under the assumption of centrally condensed stars and aligned rotational axes, the Roche lobe filling factor only depends on the mass ratio and separation of the stars, and on their radii and synchronisation factors. We calculated the Roche potential of the binary according to the formulae given in Appendix B. From the determined radii and vsini we obtain synchronisation factors s = Porb/Prot of s1 = 0.756 ± 0.038 and s2 = 1.039 ± 0.067 for the primary and secondary component, respectively. The rotation of the secondary is consistent with synchronous whereas the primary rotates with a significantly subsynchronous velocity. Figure 15 shows a cut through the equipotential surfaces of the Roche potential in the x–y (orbital) plane for the case of synchronous rotation of the secondary. All axes are in units of the separation, and the inner Lagrangian point L1 and the substellar surface point of the secondary P2 are marked. It can be seen that the secondary does not fill its Roche lobe (RL). The filling factor, defined as the ratio of P2 to L1, is 0.72. Even if we vary all input values, i.e. q, a, R1, R2, and s1 within their 1σ error limits, we get a filling factor not larger than 0.84. We therefore reaffirm our conclusion that the system is detached.
 |
Fig. 16 Composite profiles from 25 orbital phase bins of the Fe ii 4957 Å line (black) and the fit with Shellspec (red). The orbital phase is given to the right. |
Kondo (1989) suggested, from extensive observations with the IUE satellite, that gas flows are present in almost all close binaries, even when the evolved star does not seem to fill its critical RL (see also Olson & Etzel 1993). To check for possible signs of activity, we did one further test using the Shellspec program (Budaj & Richards 2004; Budaj et al. 2005) in its modified version Shellspec07_inverse (Tkachenko et al. 2009). The program is able to fit the line profiles from a time series of composite spectra using two optimised synthetic spectra. It also accounts for the Roche geometry of close binaries. We used the program to compute synthetic profiles of the Fe ii 4957 Å line based on the parameters listed in Table 4 and the last column of Table 5. Then we divided the orbit into 25 phase bins and coadded the spectra whenever more than one spectrum falls into the corresponding bin. In the result, each bin represents between one and four spectra. Figure 16 shows that the observed profiles are very well fitted by those computed with Shellspec, except for the spectrum at the bottom. The reason for the discrepancy very near to primary eclipse is that the line profiles change too rapidly in shape at this phase to be averaged over the bin size used. Figure 17 shows the fit of the single observed profiles around primary eclipse and it can be seen that also here our model works well. The Shellspec program allows the O−C residuals to be inspected for mass-transfer effects like gas streams or an accretion disc, or remnants of past activity like an inhomogeneous distribution of dense circumbinary matter typical for semi-detached (Algol-type) systems. None of these effects could be found here: the two-dimensional (wavelength versus orbital phase) O−C distribution (see Tkachenko et al. 2009, 2010) is totally flat. Moreover, the almost perfect fit of the line profiles during primary eclipse (Fig. 17) confirms our assumption that the rotation axis is aligned with the orbital axis (the question of spin-orbit alignment was recently raised due to new observations of the detached EB AS Cam, (see Pavlovski et al. 2011; Albrecht et al. 2009).
7. Discussion
Evolution. Although we actually observe a detached system it is clear that the secondary component, with a mass of 0.2 M⊙, a radius of 1.1 R⊙ and a Teff of 6000 K, can only result from mass loss in the past. Compared to “typical” Algol-type systems, KIC 10661783 has a short orbital period, a very low mass ratio and a primary star (the former mass-gainer) which rotates subsynchronous. There is a small group of stars that is characterised by the combination of short period, low mass ratio, oversized secondary and overluminous components. The stars have been frequently discussed as the subgroup of the R CMa stars, although this subgroup is regarded skeptically because of the inaccuracies of many of the assigned parameter values at the time it was established (see Varricatt & Ashok 1999 for a discussion and Budding & Butland 2011 for R CMa). Such binaries are thought to develop according to the so-called case B scenario (Ziółkowski 1969; Paczyński 1971) where the Roche lobe overflow starts when the donor star reaches its critical Roche lobe during rapid expansion after the exhaustion of hydrogen in its centre, i.e. prior to core helium burning. The secondary component in this state is oversized and overluminous and its thermonuclear power is generated in a hydrogen-burning shell surrounding a degenerate helium core. Possible conservative evolutionary scenarios have been discussed by e.g. Nelson & Eggleton (2001) and Eggleton & Kiseleva-Eggleton (2002). Sarna (2008) developed an evolutionary model for OGLEGC 228, a system that closely resembles many of the parameters of the KIC 10661783 system (see Table 8 and below). The pure conservative model predicts progenitors of about equal masses of around 0.9 M⊙ in an orbit with only a slightly longer period than actually observed. On the other hand, due to the thick envelope reacting to accretion, such low-mass systems as the R CMa stars should rapidly evolve into contact configurations (see Webbink 1977; Sarna & Ziolkowski 1988; Budding 1989; Budding & Butland 2011) so that non-conservative evolution with mass and angular momentum loss from the system can be assumed (Tomkin 1985). To avoid the strong influence of the convective zone, Sarna & De Greve (1996,SDG hereinafter), estimate that the initial mass of the secondary must be higher than 2.5 M⊙ so its observed remnant mass exceeds 0.3 M⊙.
Chemical abundance. The iron abundance as well as the averaged metal abundance of the primary are solar within the measurement errors. For the secondary, both values are about 0.3 dex below solar. The carbon abundance determined for the primary of KIC 10661783 is −0.14 ± 0.28 dex below the solar value (i.e. solar within the large errorbars); that of the secondary component is depleted (−0.79 ± 0.25 dex relative to solar). Both are typical values for Algol systems, as can be seen from a compilation of nine Algols with derived carbon abundances of the primary and 15 Algols with carbon abundances of the secondary given by SDG. In this compilation, the carbon abundance of the primary ranges from −0.41 to +0.06 dex (−0.2 ± 0.2 dex on average). For the secondary, carbon is depleted in all cases, with an average value of −0.7 ± 0.4 dex. The nitrogen abundance of KIC 10661783 could only be determined for its primary component. The enhanced value (+1.21 ± 0.34 dex above solar) is expected by SDG from evolutionary models for the secondary component; no estimations for the primary are given.
Comparison of object parameters.
Comparison with known Algol-type systems. Ibanoǧlu et al. (2006) compiled well-determined absolute parameters of Algol-type stars. We searched their compilation for systems with extremely low mass ratios. The stars with the lowest mass ratios in the list of 74 detached binaries are AR Cas (q = 0.315) and Alpha CrB (q = 0.357). Both stars are EBs consisting of two main sequence (MS) stars. Among the 61 semidetached systems we find 14 candidates with q < 0.2. Restricting the selection to short-period Algols with P < 5 d, nine systems remain. The radius of the secondary of only four of these, namely R CMa, AS Eri, ST Per, and XZ Sgr is less than 3 R⊙. The parameters of our object closest to those of R CMa and AS Eri, as can be seen from Table 8. We added one further object, OGLEGC 228 found by Kaluzny et al. (2007) as the blue straggler V228 in the globular cluster 47 Tuc. This semi-detached Algol system closely resembles the short period, the low secondary-star mass and radius, and the temperatures of both components of KIC 10661783, whereas the total mass of KIC 10661783 is very close to that of AS Eri. KIC 10661783 differs by one property from all previously found R CMa-type objects, however, in that it is a detached system.
8. Conclusions
We successfully disentangled the spectra of the primary and the faint secondary component of KIC 10661783. The analysis of the decomposed spectra gave us the effective temperatures of the stars, and radial velocities derived with TODCOR yielded an accurate measurement of the mass ratio of components. These quantities were used as input parameters to a new modelling of the Kepler light curve, resulting in the first measurement of the masses and radii of the stars. The Teff of the secondary determined from the LC analysis is 6000 ± 100 K, in good agreement with the spectroscopically derived value of 5980 ± 72 K. We also included the determination of the continuum flux ratio between the stars into the spectral analysis. The flux ratio of 0.062 at 5000 Å derived in this way is in agreement within the error bars with the V-band light ratio of 0.065 calculated from the LC solution.
The main conclusion from the combined spectroscopic-photometric analysis is that the system is detached. The measured mass ratio and orbital separation allowed us, together with the finding that the secondary component rotates synchronously, to confirm this conclusion directly using the Roche model. The maximum filling factor of the secondary component within the 1σ errors of all input parameters is 0.84. Independently of this finding, no signs of emission effects, associated with the presence of circumbinary matter and often seen in Algol binaries, could be found from applying the Shellspec program to the observed composite spectra.
The short orbital period and the very low mass ratio make KIC 10661783 a member of the “R CMa-type group”. It is, however, the only R CMa-like system observed so far that is in a detached state and rotates subsynchronously. There are tenable reasons for these properties, such as mass and angular momentum loss by non-conservative mass transfer and magnetic braking. The unusual combination of short period and low mass ratio in this group may also be related to angular momentum redistribution in the presence of third bodies as suspected by e.g. Budding & Butland (2011). This could be relevant to the present case, where orbital angular momentum may well have been redistributed in this old Algol, while tidal coupling, given the low mass of the secondary, may have been insufficient to spin up the primary. Other possible scenarios have been discussed in Sect. 7.
A detailed evolutionary model of the system is beyond the scope of this paper. We instead looked for comparable objects in the literature. The star that best resembles the parameters of our system is OGLEGC 228, the blue straggler V228 in the globular cluster 47 Tuc. An attempt by Sarna (2008) to derive a model of its evolution was limited by the inclusion of pure conservative mass transfer. Models with non-conservative mass transfer, on the other hand, have been not applied so far to Algol-type systems of such low mass ratio.
In summary, KIC 10661783 is the short-period Algol-type star with the lowest mass ratio ever observed. Although it has properties typical of an R CMa object and the primary shows δ Sct-type oscillations like the oEA stars, it differs from both groups by the fact that it is a detached system. Whereas the stellar parameters of the primary component derived in this work will support future asteroseismic modelling of its pulsations, the unusually low mass of the secondary will be a challenge for future evolutionary modelling.
Online material
Appendix A: Determination of the flux ratios
Appendix A.1: Basics
Let
Fk, k = 1,2
be the line fluxes of the two components of the binary and
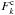 the
corresponding continuum fluxes. The observed composite spectrum normalised to the
common continuum of all components is
the
corresponding continuum fluxes. The observed composite spectrum normalised to the
common continuum of all components is 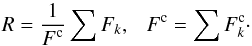 (A.1)KOREL delivers the
decomposed spectra normalised to the common continuum of the composite input spectrum,
(A.1)KOREL delivers the
decomposed spectra normalised to the common continuum of the composite input spectrum,
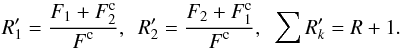 (A.2)The
wavelength-dependent ratios of the single continuum fluxes to the total flux are
(A.2)The
wavelength-dependent ratios of the single continuum fluxes to the total flux are
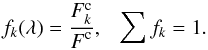 (A.3)We want to calculate
the decomposed spectra normalised to the continua of the single components,
(A.3)We want to calculate
the decomposed spectra normalised to the continua of the single components,
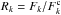 . Introducing
the line depths,
. Introducing
the line depths, 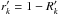 and
rk = 1 −Rk,
we simply get
and
rk = 1 −Rk,
we simply get 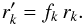 (A.4)For the
comparison with the synthetic spectra,
Sk, we replace the
rk in Eq. (A.4) by
sk = 1 −Sk.
As a measure of the goodness of fit, we use
(A.4)For the
comparison with the synthetic spectra,
Sk, we replace the
rk in Eq. (A.4) by
sk = 1 −Sk.
As a measure of the goodness of fit, we use 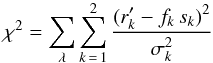 (A.5)where
the
(A.5)where
the 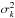 stand for
the accuracy of the line depths in the decomposed spectra. Since we compare the
spectra on the scale of the non-normalised decomposed ones, it will be
σ1 = σ2. Setting
f1 = 1 −f2 and derivating
Eq. (A.5) with respect to
f2, we finally get
stand for
the accuracy of the line depths in the decomposed spectra. Since we compare the
spectra on the scale of the non-normalised decomposed ones, it will be
σ1 = σ2. Setting
f1 = 1 −f2 and derivating
Eq. (A.5) with respect to
f2, we finally get 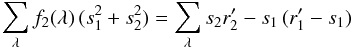 (A.6)from
which we can determine the optimum value of f2 (usually by
developing f2 into a polynomial of low degree in
λ and solving the resulting system of linear equations).
(A.6)from
which we can determine the optimum value of f2 (usually by
developing f2 into a polynomial of low degree in
λ and solving the resulting system of linear equations).
Appendix A.2: The optimum, continuum corrected solution
During the spectrum reduction, the observed composite spectrum is not exactly
normalised to the real local continuum but to some pseudo-continuum. We introduce
correction factors αk(λ)
in the sense 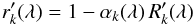 (A.7)where
(A.7)where
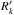 are the
wrongly normalised decomposed spectra. The
αk can be determined from spline fits
are the
wrongly normalised decomposed spectra. The
αk can be determined from spline fits
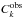 to the
uppermost points in the decomposed spectra
to the
uppermost points in the decomposed spectra 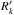 and
and
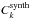 to those in
the synthetic spectra Sk. To compute the
pseudo-continua on the scale of the non-normalised decomposed spectra, the latter
spline fit has to be rescaled according to Eq. (A.4) and we get
to those in
the synthetic spectra Sk. To compute the
pseudo-continua on the scale of the non-normalised decomposed spectra, the latter
spline fit has to be rescaled according to Eq. (A.4) and we get 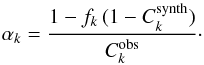 (A.8)
(A.8)
The occurrence of the so far unknown fk
in Eq. (A.8) does not complicate the
calculations because the continuum correction can be included into Eq. (A.5) to solve for the optimum values:
inserting the continuum-corrected 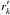 into Eq. (A.5) and derivating with respect to
f2 gives
into Eq. (A.5) and derivating with respect to
f2 gives 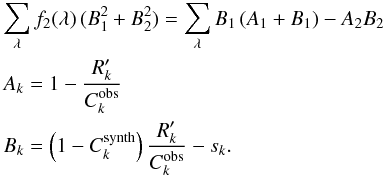 (A.9)After
solving Eq. (A.9) for
f2, χ2 is calculated from
Eq. (A.5). This can be done on a grid
of synthetic spectra sk to find the
minimum in χ2 and the corresponding optimum atmospheric
parameters. The renormalised decomposed spectra follow from Eqs. (A.4) and (A.7) to
(A.9)After
solving Eq. (A.9) for
f2, χ2 is calculated from
Eq. (A.5). This can be done on a grid
of synthetic spectra sk to find the
minimum in χ2 and the corresponding optimum atmospheric
parameters. The renormalised decomposed spectra follow from Eqs. (A.4) and (A.7) to 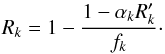 (A.10)
(A.10)
Appendix B: The Roche model
The Roche model is valid for centrally condensed stars where the gravitational
potential can be considered as the potential of point masses and, in the standard case,
for stars that rotate synchronously with the orbit and with rotation axes
perpendicularly aligned to the orbital plane. For reference, we give here the expression
for the Roche potential in the reference frame co-rotating with star 1 for the more
general case that star 1 rotates non-synchronously (see e.g. Bisikalo et al. 1999): ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{Eq1} \Phi(x,y,z) &=& -\frac{\d 1}{\d r_1}-\frac{\d q}{\d r_2} \nonumber\\ && -\frac{\d 1+q}{\d 2}\left[(x-x_{\rm c})^2+y^2-(1-s^2)(x^2+y^2)\right]. \end{eqnarray}](/articles/aa/full_html/2013/09/aa21400-13/aa21400-13-eq169.png) (B.1)All
coordinates have their origin in the centre of star 1 and are in units of the separation
a between the two stars. x points to star 2,
z along the rotation axis of star 1, and y lies in
the orbital plane to span a right-handed coordinate system.
q = M2/M1
is the mass ratio,
(B.1)All
coordinates have their origin in the centre of star 1 and are in units of the separation
a between the two stars. x points to star 2,
z along the rotation axis of star 1, and y lies in
the orbital plane to span a right-handed coordinate system.
q = M2/M1
is the mass ratio, 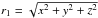 the distance to the centre of star 1,
the distance to the centre of star 1, 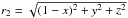 the distance to star 2, and
xc = q/(1 +q).
The synchronisation factor is
s = Ωrot/Ωorb.
the distance to star 2, and
xc = q/(1 +q).
The synchronisation factor is
s = Ωrot/Ωorb.
The Roche potential given by Eq. (B.1),
multiplied by −1, can be written as 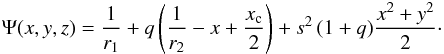 (B.2)The
shapes of the stars follow from the equipotential surfaces passing through the
substellar surface points P:
(B.2)The
shapes of the stars follow from the equipotential surfaces passing through the
substellar surface points P: 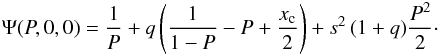 (B.3)The
position of the inner Lagrangian point L1 is calculated from
setting the derivative
dΨ(x,0,0)/dx to
zero and solving
(B.3)The
position of the inner Lagrangian point L1 is calculated from
setting the derivative
dΨ(x,0,0)/dx to
zero and solving ![\appendix \setcounter{section}{2} \begin{equation} \frac{\d 1}{\d x^2}+q\left[1-\frac{\d 1}{\d (1-x)^2}\right]-s^2\,(1+q)\,x = 0 \end{equation}](/articles/aa/full_html/2013/09/aa21400-13/aa21400-13-eq180.png) (B.4)numerically. The
radius rs that describes a sphere of the
same volume as the critical Roche lobe (the surface of the Roche potential through
L1) can be approximated with an accuracy of 1 %
(Eggleton 1983) by
(B.4)numerically. The
radius rs that describes a sphere of the
same volume as the critical Roche lobe (the surface of the Roche potential through
L1) can be approximated with an accuracy of 1 %
(Eggleton 1983) by
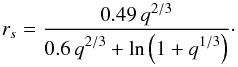 (B.5)
(B.5)
For a synchronously rotating star, this radius can be used to check if the star fills its critical Roche lobe or not. Instead, we used the filling factor f = P2/L1 as the more accurate criterion, where P2 is the substellar surface point of the secondary component (see Fig. 15). It is f = 1 when the star fills its critical Roche lobe, i.e. when P2 reaches the Lagrangian point L1.
Acknowledgments
This research is based on observations obtained with the HERMES spectrograph, which is supported by the Fund for Scientific Research of Flanders (FWO), Belgium, the Research Council of K.U.Leuven, Belgium, the Fonds National Recherches Scientific (FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland and the Thüringer Landessternwarte Tautenburg, Germany. It has made use of the Vienna Atomic Line Database (VALD, Kupka et al. 2000). JS acknowledges financial support from STFC in the form of an Advanced Fellowship. AT acknowledges funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 227224 (PROSPERITY). The authors thank the referee, Prof. Edwin Budding, for his very useful comments that helped us to improve the article remarkably.
References
- Albrecht, S., Reffert, S., Snellen, I. A. G., & Winn, J. N. 2009, Nature, 461, 373 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bisikalo, D. V., Boyarchuk, A. A., Kuznetsov, O. A., & Chechetkin, V. M. 1999, Astron. Rep., 43, 229 [NASA ADS] [Google Scholar]
- Budaj, J., & Richards, M. T. 2004, Contributions of the Astronomical Observatory Skalnaté Pleso, 34, 167 [Google Scholar]
- Budaj, J., Richards, M. T., & Miller, B. 2005, ApJ, 623, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Budding, E. 1989, Space Sci. Rev., 50, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Budding, E., & Butland, R. 2011, MNRAS, 418, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P., & Kiseleva-Eggleton, L. 2002, ApJ, 575, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Figueira, P., Pepe, F., Lovis, C., & Mayor, M. 2010, A&A, 515, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Figueira, P., Kerber, F., Chacon, A., et al. 2012, MNRAS, 420, 2874 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, R. 1973, MNRAS, 162, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Hadrava, P. 1995, A&AS, 114, 393 [NASA ADS] [Google Scholar]
- Hadrava, P. 2006, A&A, 448, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hensberge, H., Ilijić, S., & Torres, K. B. V. 2008, A&A, 482, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ibanoǧlu, C., Soydugan, F., Soydugan, E., & Dervişoǧlu, A. 2006, MNRAS, 373, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Ilijic, S. 2004, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, eds. R. W. Hilditch, H. Hensberge, & K. Pavlovski, ASP Conf. Ser., 318, 107 [Google Scholar]
- Kaluzny, J., Thompson, I. B., Rucinski, S. M., et al. 2007, AJ, 134, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kondo, Y. 1989, Space Sci. Rev., 50, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astron., 9, 590 [Google Scholar]
- Lehmann, H., & Tkachenko, A. 2012, in IAU Symp. 282, eds. M. T. Richards & I. Hubeny, 395 [Google Scholar]
- Lehmann, H., Tkachenko, A., Semaan, T., et al. 2011, A&A, 526, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, P., & Breger, M. 2004, in The A-Star Puzzle, eds. J. Zverko, J. Ziznovsky, S. J. Adelman, & W. W. Weiss, IAU Symp., 224, 786 [Google Scholar]
- Mazeh, T., & Zucker, S. 1992, in IAU Colloq. 135: Complementary Approaches to Double and Multiple Star Research, eds. H. A. McAlister, & W. I. Hartkopf, ASP Conf. Ser., 32, 164 [Google Scholar]
- Mazeh, T., & Zucker, S. 1994, Ap&SS, 212, 349 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Mkrtichian, D. E., Kusakin, A. V., Gamarova, A. Y., & Nazarenko, V. 2002, in IAU Colloq. 185: Radial and Nonradial Pulsations as Probes of Stellar Physics, eds. C. Aerts, T. R. Bedding, & J. Christensen-Dalsgaard, ASP Conf. Ser., 259, 96 [Google Scholar]
- Mkrtichian, D. E., Nazarenko, V., Gamarova, A. Y., et al. 2003, in Interplay of Periodic, Cyclic and Stochastic Variability in Selected Areas of the H-R Diagram, ed. C. Sterken, ASP Conf. Ser., 292, 113 [Google Scholar]
- Nelson, C. A., & Eggleton, P. P. 2001, ApJ, 552, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Ohta, Y., Taruya, A., & Suto, Y. 2005, ApJ, 622, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, E. C., & Etzel, P. B. 1993, AJ, 106, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1971, ARA&A, 9, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovski, K., & Hensberge, H. 2005, A&A, 439, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlovski, K., Tamajo, E., Koubský, P., et al. 2009, MNRAS, 400, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovski, K., Southworth, J., & Kolbas, V. 2011, ApJ, 734, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Pojmanski, G. 1997, Acta Astron., 47, 467 [NASA ADS] [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sarna, M. J. 2008, in Hot Subdwarf Stars and Related Objects, eds. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 59 [Google Scholar]
- Sarna, M. J., & De Greve, J.-P. 1996, QJRAS, 37, 11 [NASA ADS] [Google Scholar]
- Sarna, M. J., & Ziolkowski, J. 1988, Acta Astron., 38, 89 [NASA ADS] [Google Scholar]
- Schlesinger, F. 1910, Publications of the Allegheny Observatory of the University of Pittsburgh, 1, 33 [NASA ADS] [Google Scholar]
- Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz, C., & Weiss, W. W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2005, A&A, 429, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J., Bruntt, H., & Buzasi, D. L. 2007, A&A, 467, 1215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J., Zima, W., Aerts, C., et al. 2011, MNRAS, 414, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Sterne, T. E. 1941, Proce. Nat. Acad. Sci., 27, 175 [Google Scholar]
- Tkachenko, A., Lehmann, H., & Mkrtichian, D. E. 2009, A&A, 504, 991 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tkachenko, A., Lehmann, H., & Mkrtichian, D. 2010, AJ, 139, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Tkachenko, A., Aerts, C., Pavlovski, K., et al. 2012, MNRAS, 424, L21 [NASA ADS] [Google Scholar]
- Tomkin, J. 1985, ApJ, 297, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Tsymbal, V. 1996, in MASS, Model Atmospheres and Spectrum Synthesis, eds. S. J. Adelman, F. Kupka, & W. W. Weiss, ASP Conf. Ser., 108, 198 [Google Scholar]
- van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- Varricatt, W. P., & Ashok, N. M. 1999, AJ, 117, 2980 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1977, ApJ, 211, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E. 1979, ApJ, 234, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E., & Van Hamme, W. 2004, Computing Binary Star Observables, Wilson-Devinney program user guide [Google Scholar]
- Ziółkowski, J. 1969, Ap&SS, 3, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, S., & Mazeh, T. 1994, ApJ, 420, 806 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
All Tables
Elemental abundances of the primary (A1) and the secondary (A2) compared to the Sun and their 1σ errors.
All Figures
 |
Fig. 1 RVs of the primary component measured from TLS (squares) and HERMES (crosses) spectra folded with the orbital period. The solid curve is based on the parameters listed in Table 5. Phase zero corresponds to Min I. |
| In the text | |
 |
Fig. 2 O−C residuals of the fit in Fig. 1, indicating the presence of the Rossiter-McLaughlin effect during primary eclipse. |
| In the text | |
 |
Fig. 3 Strong and faint Fe ii 4957 Å lines of the primary and secondary, respectively. The vertical axis gives the orbital phase of observation, and secondary eclipse occurs at the centre of the image. The elongation in RV (horizontal axis) corresponds to the velocity semiamplitudes given in Table 5. |
| In the text | |
 |
Fig. 4 Decomposed spectra of the primary and secondary components. The latter is shifted upwards by 0.05 for clarity. |
| In the text | |
 |
Fig. 5 Comparison of the decomposed Hβ line profiles of the primary component obtained with CRES (black) and with KOREL (red). |
| In the text | |
 |
Fig. 6 Chemical abundances of the primary (crosses) and the secondary (open circles) components, relative to solar. Chemical elements are sorted by their atomic numbers. The dashed and dotted lines show the weighted mean for the primary and secondary stars, respectively. |
| In the text | |
 |
Fig. 7 Rossiter-McLaughlin effect: synthetic line profiles computed for different phases around primary eclipse (left) and the RVs computed from these profiles (right). |
| In the text | |
 |
Fig. 8 Flux ratio (top) and vsini of the primary component (bottom) determined with TODCOR, folded with the orbital period. Phase zero corresponds to Min I. |
| In the text | |
 |
Fig. 9 RVs of the primary component determined with TODCOR. The solid curve shows the orbital solution calculated with PHOEBE. RVs included into the solution are shown by plus signs, outliers by crosses. The lower panel shows the O–C residuals. |
| In the text | |
 |
Fig. 10 As Fig. 9 but for the secondary component. |
| In the text | |
 |
Fig. 11 Left: LSD profiles computed from all HERMES spectra, vertically arranged according to orbital phase. Profiles distorted by the RME are shown in red. Right: differential LSD spectra from different nights (see text). The synthetic LSD profile of the primary is overplotted for a better distinction between line profile and continuum regions. |
| In the text | |
 |
Fig. 12 Comparison of the LSD profile observed for the primary component (thick) with synthetic LSD profiles computed for vsini values of 75 (dotted), 80 (solid), and 85 km s-1 (dashed). |
| In the text | |
 |
Fig. 13 Comparison of the LSD profile observed for the secondary component (thick) with synthetic LSD profiles computed for vsini values of 38 (dotted), 48 (solid), and 58 km s-1 (dashed). |
| In the text | |
 |
Fig. 14 Best fit of the phase-binned Kepler short-cadence data of KIC 10661783 using wd2004. The fitted data are shown in the upper part of the plot and the residuals in the lower part of the plot. |
| In the text | |
 |
Fig. 15 Cut through the Roche equipotential surfaces in the x–y plane. The primary component is shown in yellow, the secondary in red colour. The plus sign marks the L1-point, the cross the P2-point. |
| In the text | |
 |
Fig. 16 Composite profiles from 25 orbital phase bins of the Fe ii 4957 Å line (black) and the fit with Shellspec (red). The orbital phase is given to the right. |
| In the text | |
 |
Fig. 17 As Fig. 16 but for single spectra around primary eclipse. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


