| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321545 | |
| Published online | 04 July 2013 | |
Online material
Appendix A: Surface with constant optical depth
The optical depth τν can be calculated
using (Rybicki & Lightman 1986; Rutten 2003) 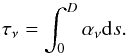 (A.1)This shows that
the optical depth depends on the frequency ν, the LOS, and the
extinction coefficient α, which also depends on the photon frequency.
To simplify the calculations we assume that the LOS is directed along the
z-axis, i.e. ds = dz. The goal is
to find the height D for which the optical depth at a given frequency
τν is constant. Because we are using
observations of the photosphere, we assume that the intensity observations are taken in
the continuum and not in the line core. In Rutten
(2003) we can find different sources for opacity in the continuum each with
their own extinction coefficient. We have bound-free transitions, free-free transitions,
Thomson scattering, and Rayleigh scattering. The most important source for the solar
photosphere comes from bound-free transitions where the hydride
H− absorb radiation to form hydrogen and a free electron
(Marshall 2003; Pradhan & Nahar 2011). From Rutten
(2003) we find that for bound-free transitions
(A.1)This shows that
the optical depth depends on the frequency ν, the LOS, and the
extinction coefficient α, which also depends on the photon frequency.
To simplify the calculations we assume that the LOS is directed along the
z-axis, i.e. ds = dz. The goal is
to find the height D for which the optical depth at a given frequency
τν is constant. Because we are using
observations of the photosphere, we assume that the intensity observations are taken in
the continuum and not in the line core. In Rutten
(2003) we can find different sources for opacity in the continuum each with
their own extinction coefficient. We have bound-free transitions, free-free transitions,
Thomson scattering, and Rayleigh scattering. The most important source for the solar
photosphere comes from bound-free transitions where the hydride
H− absorb radiation to form hydrogen and a free electron
(Marshall 2003; Pradhan & Nahar 2011). From Rutten
(2003) we find that for bound-free transitions
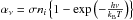 ,
where σ is a constant that depends on the atom/ion involved in the
bound-free transition, ni is the number
density in the ionising level, h is the Planck constant,
kB is the Boltzmann constant, T is the
temperature of the plasma, and ν is the frequency. We assume that
ni is proportional to the density
ρ, thus the monochromatic optical depth is
,
where σ is a constant that depends on the atom/ion involved in the
bound-free transition, ni is the number
density in the ionising level, h is the Planck constant,
kB is the Boltzmann constant, T is the
temperature of the plasma, and ν is the frequency. We assume that
ni is proportional to the density
ρ, thus the monochromatic optical depth is
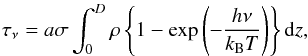 where
a indicates the fraction of ionisation. We can now linearise both the
density and the temperature to find
where
a indicates the fraction of ionisation. We can now linearise both the
density and the temperature to find 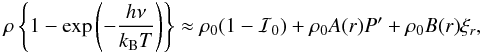 where
ℐ0, A(r), and
B(r) are given by
where
ℐ0, A(r), and
B(r) are given by
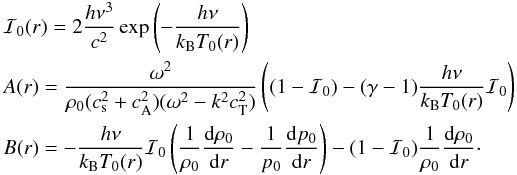
The optical depth (Eq. (A.1)) is thus
given by 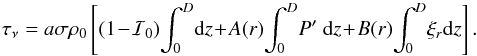 (A.2)In general,
D is a function of r,ϕ, and
t, but since we are dealing with axisymmetric modes, we have
D(r,t). We linearise
D(r,t) = D0 + D′(r,t)
and substitute in Eq. (A.2) to find
(A.2)In general,
D is a function of r,ϕ, and
t, but since we are dealing with axisymmetric modes, we have
D(r,t). We linearise
D(r,t) = D0 + D′(r,t)
and substitute in Eq. (A.2) to find
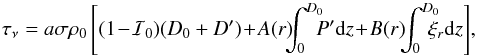 (A.3)where we neglected
higher-order terms. Because the optical depth
τν is constant, the zeroth-order terms in
Eq. (A.3) show
(A.3)where we neglected
higher-order terms. Because the optical depth
τν is constant, the zeroth-order terms in
Eq. (A.3) show 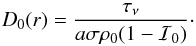 (A.4)To find
D′ we look at the first-order terms in Eq. (A.3) and find
(A.4)To find
D′ we look at the first-order terms in Eq. (A.3) and find
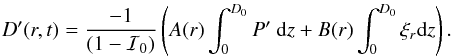 Since
both P′ and ξr
are proportional to exp{i(kz − ωt)},
Since
both P′ and ξr
are proportional to exp{i(kz − ωt)}, 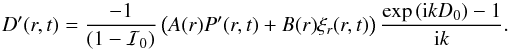 (A.5)The equation
for a surface with constant optical depth is given by
g(r,z,t) ≡ z − D(r,t).
In the uniform case we have D0 constant,
A(r) constant, and
B(r) = 0, thus
g(r,z,t) has a similar form as the surface that
follows the motions of the plasma (i.e.
f(r,ϕ,z,t) ≡ z − ξz(r,ϕ,z = 0,t)).
We calculate the normal to the surface
g
(A.5)The equation
for a surface with constant optical depth is given by
g(r,z,t) ≡ z − D(r,t).
In the uniform case we have D0 constant,
A(r) constant, and
B(r) = 0, thus
g(r,z,t) has a similar form as the surface that
follows the motions of the plasma (i.e.
f(r,ϕ,z,t) ≡ z − ξz(r,ϕ,z = 0,t)).
We calculate the normal to the surface
g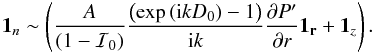 We
relate a surface element dS to an elemental surface element in the
horizontal plane dSh, i.e.
We
relate a surface element dS to an elemental surface element in the
horizontal plane dSh, i.e.
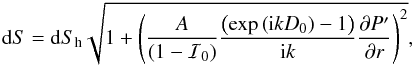 which
in a linear approximation is
dS = dSh = rdrdϕ.
This shows that integrating over the surface where
τν is constant or integrating over the
surface that follows the motions of the plasma is identical, since for a uniform
equilibrium and in a linear expansion the elemental surface elements are the same.
which
in a linear approximation is
dS = dSh = rdrdϕ.
This shows that integrating over the surface where
τν is constant or integrating over the
surface that follows the motions of the plasma is identical, since for a uniform
equilibrium and in a linear expansion the elemental surface elements are the same.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


