| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A146 | |
| Number of page(s) | 20 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321415 | |
| Published online | 16 July 2013 | |
Online material
Appendix A: The blowout timescale
Particles with high β ratios are removed from the system by radiation pressure. Here, we derive the typical timescale for this process, for the case of β ≫ 1. In this limit, the transverse movement of the particles is small compared to the radial movement, and only the radial acceleration of the particle needs to be considered.
Appendix A.1: The gas free case
We need to consider the forces of gravity and direct radiation pressure (the PR drag force is negligibly small, and we do not consider gas drag at this stage). These forces are given by 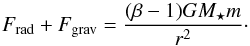 (A.1)For small radial displacements Δr, the acceleration
(A.1)For small radial displacements Δr, the acceleration 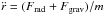 can be assumed to be independent of r, and the displacement as a function of time is given by
can be assumed to be independent of r, and the displacement as a function of time is given by 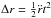 . The resulting timescale is
. The resulting timescale is 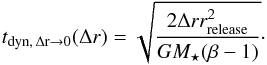 (A.2)At large distances from the release point, the acceleration tends to zero, and the velocity of the particle approaches a constant:
(A.2)At large distances from the release point, the acceleration tends to zero, and the velocity of the particle approaches a constant: 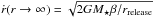 (Lecavelier des Etangs et al. 1998). Hence, for large displacements, the removal happens on a timescale of
(Lecavelier des Etangs et al. 1998). Hence, for large displacements, the removal happens on a timescale of 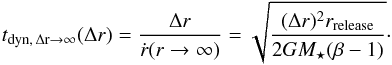 (A.3)Adding Eqs. (A.2) and (A.3) in quadrature leads to the removal timescale
(A.3)Adding Eqs. (A.2) and (A.3) in quadrature leads to the removal timescale 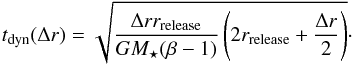 (A.4)
(A.4)
Comparing this equation with a numerical evaluation of the equation of motion shows that its relative errors are less than 5% for the values of β and rrelease considered here.
We define tdyn as the time it takes for a particle to fly from its release point (rrelease) to a point twice that radial distance from the star (2rrelease). This is motivated by the fact that the small grains are seen in a very narrow radial range, so only the time they spend close to the release point is relevant. Setting Δr = rrelease = r gives the blowout timescale given by Eq. (31).
Appendix A.2: The high gas density case
For high gas densities, the gas drag force cannot be ignored. Since the particles considered here are small (compared to the mean free path of the gas molecules), and their velocities are low (compared to the sound speed of the gas), the gas drag force is given by the subsonic Epstein drag law. It is given by 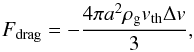 (A.5)where ρg is the mass density of the gas, Δv is the relative speed between the dust grain and the gas, and vth is the mean thermal speed of the gas. The latter is given by
(A.5)where ρg is the mass density of the gas, Δv is the relative speed between the dust grain and the gas, and vth is the mean thermal speed of the gas. The latter is given by 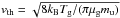 , where μg is the molecular weight of gas molecules, mu is the atomic mass unit, kB is the Boltzmann constant, and Tg is the temperature of the gas. To calculate vth, we assume that the gas temperature equals the dust temperature (Tg = Td), and that the gas consists of the same molecules as the dust grains (μg = μd).
, where μg is the molecular weight of gas molecules, mu is the atomic mass unit, kB is the Boltzmann constant, and Tg is the temperature of the gas. To calculate vth, we assume that the gas temperature equals the dust temperature (Tg = Td), and that the gas consists of the same molecules as the dust grains (μg = μd).
For high gas densities, the particles quickly reach the terminal velocity vterm, which is found by solving Frad + Fgrav + Fdrag = 0 for Δv. This gives 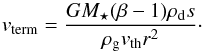 (A.6)In the high gas density case, the average velocity over the radial range Δr can be approximated by the terminal velocity. The blowout timescale for high gas densities is then found from tdyn, ρg → ∞(ρg,Δr) = Δr/vterm, which leads to Eq. (32).
(A.6)In the high gas density case, the average velocity over the radial range Δr can be approximated by the terminal velocity. The blowout timescale for high gas densities is then found from tdyn, ρg → ∞(ρg,Δr) = Δr/vterm, which leads to Eq. (32).
 |
Fig. B.1
Bayesian probability curves obtained when fitting models to the warm component with approach 1 (inner density slope fixed to 10, free outer density slope α). |
| Open with DEXTER | |
 |
Fig. B.2
Bayesian probability curves obtained when fitting models to the warm component with approach 2 (outer density slope fixed to 1.5, free inner density slope α). The analysis uses some prior information regarding the grain sizes P(a < ablow/10 = 0). |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


