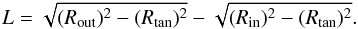| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 28 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321188 | |
| Published online | 11 June 2013 | |
Online material
Appendix A: Azimuthally averaged line emissivities
In the following we describe the procedure we used to calculate the radial distribution of the azimuthally averaged integrated intensity per unit length of a spectral line. Assuming a flat rotation curve and circular motions, the distance to the Galactic center R for a given data point with Galactic longitude l, latitude b, and local standard of rest (LSR) velocity VLSR, is given by 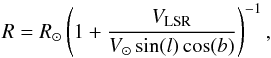 (A.1)where R⊙ is the distance from the sun to the Galactic center and V⊙ is the orbital velocity of the sun with respect to the Galactic center. We adopt the IAU recommended values of R⊙ = 8.5 kpc and V⊙ = 220 km s-1. We can invert Eq. (A.1) to relate the observed LSR velocity of the emission to the Galactocentric distance through
(A.1)where R⊙ is the distance from the sun to the Galactic center and V⊙ is the orbital velocity of the sun with respect to the Galactic center. We adopt the IAU recommended values of R⊙ = 8.5 kpc and V⊙ = 220 km s-1. We can invert Eq. (A.1) to relate the observed LSR velocity of the emission to the Galactocentric distance through 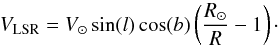 (A.2)We divided the Galaxy in a set of concentric rings, with a central radial distance R and a radial extent ΔR = Rout − Rin. For a given ring, we used Eq. (A.2) to calculate the corresponding interval limits in VLSR. We then calculated the integrated intensity I(l,R) within this LSR velocity range. The integrated intensity depends on the path length crossed by a given line of sight, L(l,Rout,Rin), and therefore we divided by this path length to calculate the integrated intensity per unit length (emissivity). The units of the emissivity are K km s-1 kpc-1. The value of L depends on the location of the Galaxy we are sampling. This dependency is illustrated in Fig. A.1 where we show a schematic of the different cases we considered for the calculation of L.
(A.2)We divided the Galaxy in a set of concentric rings, with a central radial distance R and a radial extent ΔR = Rout − Rin. For a given ring, we used Eq. (A.2) to calculate the corresponding interval limits in VLSR. We then calculated the integrated intensity I(l,R) within this LSR velocity range. The integrated intensity depends on the path length crossed by a given line of sight, L(l,Rout,Rin), and therefore we divided by this path length to calculate the integrated intensity per unit length (emissivity). The units of the emissivity are K km s-1 kpc-1. The value of L depends on the location of the Galaxy we are sampling. This dependency is illustrated in Fig. A.1 where we show a schematic of the different cases we considered for the calculation of L.
In Case 1a we considered rings with outer radii inside the solar circle (Rout ≤ R⊙) and inner radius Rin larger than the radius of the tangent Rtan = | R⊙sin(l) |. In this case a given ring is crossed twice by a given LOS. The path length for one of these crossings is given by,
 |
Fig. A.1
Schematic of the Milky Way divided by a set of rings centered at the Galactic center. The two thick arrows originating from the Sun (shown as a circle) correspond to two lines-of-sight, one looking toward the inner Galaxy and the other toward the outer Galaxy. The dashed lines represent the distance to the Galactic center (R⊙) and the distance to the tangent point (Rtan) for the line of sight that goes towards the inner Galaxy. The thin lines point to the different path lengths crossed by the lines-of-sight that correspond to the different cases considered in the text. |
| Open with DEXTER | |
In Case 1b we considered rings with Rin < Rtan ≤ Rout. In this case a ring is crossed only once and the path length is given by, 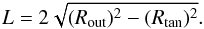 (A.4)In Case 2 we considered LOSs that cross rings in the outer Galaxy with Rin > R⊙. These rings are crossed once and the path length is given by Eq. (A.3).
(A.4)In Case 2 we considered LOSs that cross rings in the outer Galaxy with Rin > R⊙. These rings are crossed once and the path length is given by Eq. (A.3).
Rings in Case 3a have Rin < R⊙ < Rout and are observed in LOSs in the range 270° > l > 90°. In this case the path length is given by the distance to the point with R = Rout, 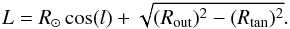 (A.5)Finally for Case 3b, we considered rings with Rin < R⊙ < Rout observed in LOSs in the range 270° < l < 90°. In this case we cross a ring twice. For the near side the path length is given by
(A.5)Finally for Case 3b, we considered rings with Rin < R⊙ < Rout observed in LOSs in the range 270° < l < 90°. In this case we cross a ring twice. For the near side the path length is given by 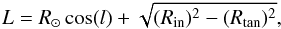 (A.6)and for the far side is given by Eq. (A.3).
(A.6)and for the far side is given by Eq. (A.3).
The final step is to average the emissivities over all samples of a given ring. This sum is done over all rings sampled by the GOT C+ survey Ns, 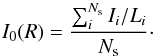 (A.7)We estimated the errors on the emissivity by propagating the errors of the individual determinations of the integrated intensity per unit length, ΔI/L, using,
(A.7)We estimated the errors on the emissivity by propagating the errors of the individual determinations of the integrated intensity per unit length, ΔI/L, using, 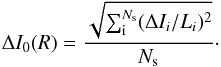 (A.8)In the top panel of Fig. A.2 we show the resulting radial distribution of the [C ii] emissivity for different values of ΔR = 0.5 kpc, 1 kpc, and 2 kpc. We can see that for larger values of ΔR the peak shifts to around 5 kpc, which is the midpoint where most of the [C ii] emission observed in the GOT C+ survey arises in the Galaxy. We adopt ΔR = 0.5 kpc to preserve the details of the [C ii] emissivity distribution. The uncertainty in the [C ii] emissivities for this selection of ΔR is typically 0.02 K km s-1 kpc-1. The bottom panel shows the number of samples (Ns) for a given ring. As we can see, rings with radii below 2 kpc are undersampled in our survey. Given that such rings are sampled by lines-of-sights with | l | < 3°, and that these LOSs are also known to have non-circular motions, we exclude these LOSs in our analysis. This exclusion has a minimal effect on emissivity distribution beyond 2 kpc.
(A.8)In the top panel of Fig. A.2 we show the resulting radial distribution of the [C ii] emissivity for different values of ΔR = 0.5 kpc, 1 kpc, and 2 kpc. We can see that for larger values of ΔR the peak shifts to around 5 kpc, which is the midpoint where most of the [C ii] emission observed in the GOT C+ survey arises in the Galaxy. We adopt ΔR = 0.5 kpc to preserve the details of the [C ii] emissivity distribution. The uncertainty in the [C ii] emissivities for this selection of ΔR is typically 0.02 K km s-1 kpc-1. The bottom panel shows the number of samples (Ns) for a given ring. As we can see, rings with radii below 2 kpc are undersampled in our survey. Given that such rings are sampled by lines-of-sights with | l | < 3°, and that these LOSs are also known to have non-circular motions, we exclude these LOSs in our analysis. This exclusion has a minimal effect on emissivity distribution beyond 2 kpc.
 |
Fig. A.2
Top: radial distribution of the [C ii] emissivity for different values of the radial extent for each ring ΔR = 0.5 kpc, 1 kpc, and 2 kpc. Bottom: the number of samples crossed by the GOT C+ lines-of-sight as a function of Galactocentric radius, for different values of ΔR. |
| Open with DEXTER | |
Appendix B: Position-velocity maps
In Figs. B.1 to B.4, we present the position-velocity maps of the [C ii], CO, and H i emission for the GOT C+ lines-of-sight with b = ± 0.5° and b = ± 1.0°. Figure B.5 shows the position-velocity maps for the different cloud types discussed in Sect. 4.1, for the GOT C+ lines-of-sight with b = ± 0.5° and b = ± 1.0°.
 |
Fig. B.1
Position-velocity maps of the Milky Way in [C ii] observed by GOT C+ for b = + 0.5°. |
| Open with DEXTER | |
 |
Fig. B.2
Position-velocity maps of the Milky Way in [C ii] observed by GOT C+ for b = − 0.5°. |
| Open with DEXTER | |
 |
Fig. B.3
Position-velocity maps of the Milky Way in [C ii] observed by GOT C+ for b = + 1.0°. |
| Open with DEXTER | |
 |
Fig. B.4
Position-velocity maps of the Milky Way in [C ii] observed by GOT C+ for b = − 1.0°. |
| Open with DEXTER | |
 |
Fig. B.5
Position velocity maps of the different cloud types defined in Sect. 4.1 for b = ± 0.5° and ±1.0°. The Mask 0 (grey) represents velocity components with only H i detected, Mask 1 (white) are components with only H i and CO detected, Mask 2 (blue) components with only H i and [C ii], Mask 3 (black) components with H i, [C ii], and CO, and Mask 4 (red) components with H i, [C ii], 12CO, and 13CO. |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.