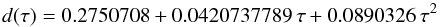| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201221020 | |
| Published online | 10 June 2013 | |
Online material
Appendix A: Landau damping of ion acoustic waves in fluid theory
Appendix A.1: Elements of kinetic description
Within the two-component kinetic theory, Landau damping is well known. Here, we give a few details only in order to compare it with fluid description presented below in Sect. A.2. Small electrostatic perturbations of the form exp( − iωt + ikz) yield the dispersion equation 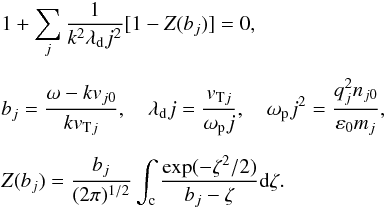 (A.1)The dispersion Eq. (A.1) describes the plasma (Langmuir) and the IA oscillations, and ζ = vz/vTj.
(A.1)The dispersion Eq. (A.1) describes the plasma (Langmuir) and the IA oscillations, and ζ = vz/vTj.
For the present case with electrons and ions and in the limit 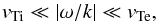 (A.2)the standard expansions may be used
(A.2)the standard expansions may be used 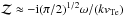 , and
, and 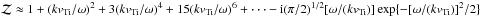 , where ω = ωr + iγ is complex and its real part is assumed to be much larger than its imaginary part. The procedure yields the dispersion equation
, where ω = ωr + iγ is complex and its real part is assumed to be much larger than its imaginary part. The procedure yields the dispersion equation 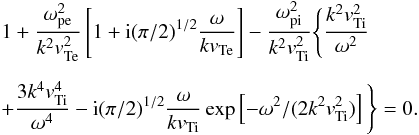 (A.3)We introduce ℑ △ (ω,k) and ℜ △ (ω,k) denoting the imaginary and real parts of Eq. (A.3), respectively. Setting the real part ℜ △ (ω,k) = 0 yields the approximate expression for the IA spectrum
(A.3)We introduce ℑ △ (ω,k) and ℜ △ (ω,k) denoting the imaginary and real parts of Eq. (A.3), respectively. Setting the real part ℜ △ (ω,k) = 0 yields the approximate expression for the IA spectrum 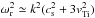 ,
, 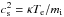 . The approximate Landau damping of the wave is obtained from
. The approximate Landau damping of the wave is obtained from 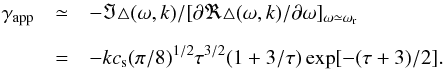 (A.4)Here, τ = Te/Ti, and we have assumed massless electrons and singly charged ions, that is, the Landau damping is due to the ions only. Otherwise, the electron contribution to the Landau damping
(A.4)Here, τ = Te/Ti, and we have assumed massless electrons and singly charged ions, that is, the Landau damping is due to the ions only. Otherwise, the electron contribution to the Landau damping 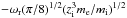 would appear in addition to the previously given Landau damping term, where zi is the ion charge number.
would appear in addition to the previously given Landau damping term, where zi is the ion charge number.
 |
Fig. A.1
Absolute value of the Landau damping of the IA wave (normalized to ωr) in terms of τ = Te/Ti. |
| Open with DEXTER | |
In Fig. A.1, we give the absolute value of the approximate (dotted line) Landau damping (8) (normalized to ωr) in terms of τ, together with the absolute value of the exact normalized Landau damping (full line) that may be obtained numerically from the general dispersion law (A.1). The nature of the dashed line will be given in Sect. A.2 below. It is seen that in the given range of τ the approximate kinetic expression (A.4) yields inaccurate values for the damping. For τ = 1, which is of interest for the solar corona, the exact Landau damping γex = 0.394ωr is larger by about a factor 2 than the approximate kinetic Landau damping γapp.
For practical purposes, we note that the exact kinetic Landau damping may conveniently be expressed in terms of τ by the following polynomial (cf. Chen 1984): 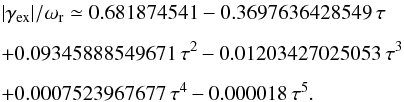 (A.5)The difference between γex and γapp follows from the fact that, in the limit τ → 1, the assumptions used to obtain the approximate kinetic damping become violated. One is thus supposed to use the rather inconvenient general dispersion Eq. (A.1), which contains an integral. Below, we show that this problem may be circumvented by using the two-fluid theory and a modeled fluid-Landau damping.
(A.5)The difference between γex and γapp follows from the fact that, in the limit τ → 1, the assumptions used to obtain the approximate kinetic damping become violated. One is thus supposed to use the rather inconvenient general dispersion Eq. (A.1), which contains an integral. Below, we show that this problem may be circumvented by using the two-fluid theory and a modeled fluid-Landau damping.
Appendix A.2: Two-fluid description
We use the linearized momentum equation for the general species α in a quasi-neutral plasma 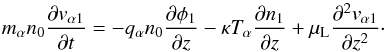 (A.6)The term with μL is the one introduced for the first time by D’Angelo et al. (1979) to describe the Landau damping effect on the fast solar wind streams with a spatially varying ratio τ( =Te/Ti) of the electron and ion temperatures. It is chosen in such a way to quantitatively describe the known properties of the Landau effect. These include the fact that the ratio d = δ/λ, between the attenuation length δ and the wavelength, is independent of the wavelength and the plasma density and dependent on τ in a prescribed way (Sessler & Pearson 1967; Andersen et al. 1968). These requirements appear to be fulfilled by
(A.6)The term with μL is the one introduced for the first time by D’Angelo et al. (1979) to describe the Landau damping effect on the fast solar wind streams with a spatially varying ratio τ( =Te/Ti) of the electron and ion temperatures. It is chosen in such a way to quantitatively describe the known properties of the Landau effect. These include the fact that the ratio d = δ/λ, between the attenuation length δ and the wavelength, is independent of the wavelength and the plasma density and dependent on τ in a prescribed way (Sessler & Pearson 1967; Andersen et al. 1968). These requirements appear to be fulfilled by 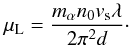 (A.7)Here,
(A.7)Here, 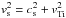 , while d(τ) satisfies a curve that is such that the attenuation is strong at τ ≈ 1 and weak for higher values of τ. It turns out that a sufficiently good choice for d(τ) is
, while d(τ) satisfies a curve that is such that the attenuation is strong at τ ≈ 1 and weak for higher values of τ. It turns out that a sufficiently good choice for d(τ) is
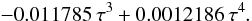 We observe that d(1) ≃ 0.4. We also use the ion continuity and in the massless electron limit from the electron momentum, we obtain just the Boltzmann distribution for electrons. This yields the dispersion equation for the Landau-damped IA wave
We observe that d(1) ≃ 0.4. We also use the ion continuity and in the massless electron limit from the electron momentum, we obtain just the Boltzmann distribution for electrons. This yields the dispersion equation for the Landau-damped IA wave 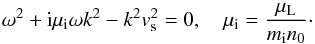 (A.8)For the complex frequency ω = ωr + iγf, we obtain
(A.8)For the complex frequency ω = ωr + iγf, we obtain 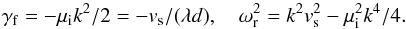 (A.9)
(A.9)
This shows that the mode oscillation frequency ωr is reduced as compared to the ideal plasma case, that is, without Landau damping. It is now appropriate to compare this fluid-modeled Landau damping γf with the exact kinetic damping given earlier. The normalized absolute fluid-modeled Landau damping | γf/ωr | ≃ 1/(2πd) is presented by the dashed line in Fig. A.1. The difference between γf and γex at τ = 1 is only 0.008. Clearly, the presented fluid-modeled Landau damping is, in fact, much more accurate than the approximate kinetic expression (A.4).
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.