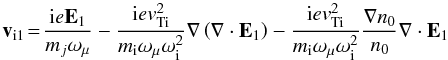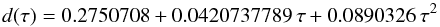| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201221020 | |
| Published online | 10 June 2013 | |
New features of ion acoustic waves in inhomogeneous and permeating plasmas ⋆
1 R. Vandervaerenlaan 16/402, 3000 Leuven, Belgium
e-mail: jvranjes@yahoo.com
2 Institute of Physics Belgrade, Pregrevica 118, 11080 Zemun, Serbia
Received: 30 December 2012
Accepted: 8 May 2013
Context. It is generally accepted that the ion acoustic (IA) wave in plasmas containing ions and electrons with the same temperature is of minor importance due to strong damping of the wave by hot resonant ions.
Aims. In this work it will be shown that the IA wave is susceptible to excitation even in hot-ion plasmas when both an electromagnetic transverse wave and a background density gradient are present in the plasma and, in addition, the wave is unstable (i.e., growing) in the case of permeating homogeneous plasmas.
Methods. The multi-component fluid theory is used to describe the IA wave susceptibility for excitation in inhomogeneous plasmas and its coupling with electromagnetic waves. The growing IA wave in permeating homogeneous plasmas is described by the kinetic theory.
Results. In plasmas with density and temperature gradients, the IA wave is effectively coupled with the electromagnetic waves. In comparison to the ordinary IA wave in homogeneous plasma, the Landau damping of the present wave is much smaller; to demonstrate this effect, a simple but accurate fluid model is presented for the Landau damping. In the case of permeating plasmas, a kinetic mechanism for the currentless IA wave instability is presented; it has a very low threshold for excitation compared with ordinary electron-current-driven kinetic instability. Such growing IA waves can effectively heat plasma in the upper solar atmosphere by a stochastic heating mechanism presented in the work.
Conclusions. The results presented in the work suggest that the role of the IA wave in the heating of the solar atmosphere (chromosphere and corona) should be reexamined.
Key words: waves / instabilities / Sun: atmosphere
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Acoustic waves have been a popular tool in models dealing with heating in the solar atmosphere from the early days of solar plasma physics (Alfvén 1947; Biermann 1948; Schwarzschild 1948; D’Angelo 1968). Unsupported by observations, these models have been replaced in the course of time by many others based on different plasma modes and on various different heating mechanisms. However, very recent observations (Bello González et al. 2010; Kneer & Bello González 2011) have revived interest in the acoustic modes. This is because large fluxes of acoustic modes, which are excited by convective motion in the photosphere, have been observed. They are only by a factor two smaller than the value presently accepted as required for a sustainable heating of the chromosphere.
Models based on wave heating in the solar atmosphere are typically based on a scheme that implies the initiation of such waves in lower layers and their consequent propagation towards the upper solar atmosphere, where they are supposed to dissipate and deposit their energy. Hence, if an observed flux of such a wave is too low or absent, its role in the heating is assumed to be unimportant. However, a wave-heating scenario may include models with waves that are generated directly on the spot, that is, in the corona itself and then dissipated, thus contributing to heating, see examples based on the drift wave theory presented in Vranjes & Poedts (2009a,b; 2010a,b) and in Vranjes (2011a,b). This implies the presence of some energy source for excitation of such waves directly in the corona. In the case of the mentioned drift wave model, the energy is stored in the gradients of background density and temperature.
In the present work we shall show that the ion acoustic (IA) waves may be produced on massive scales directly in the upper solar atmosphere. Their energy may further be transformed into internal energy of the plasma by at least two different mechanisms, which will be discussed. We shall describe two very different possible sources for their excitation.
-
a)
The first source are simply electromagnetic transverse (light)waves, which are undoubtedly widespread in an environmentsuch as the solar atmosphere. It is shown that, in the presence ofsuch waves, IA waves are susceptible to excitation, providedthere is a simultaneous presence of density gradient. A typical en-vironment for this mechanism to work is provided by solar mag-netic structures, where a density gradient should be ubiquitousin the direction perpendicular to the magnetic field. However, itshould be stressed that the magnetic field plays no role in this exci-tation mechanism; its role is reduced only to equilibrium plasmaconfinement. All that is necessary is the presence of a transversewave and density gradient. The latter can in fact be balanced by atemperature gradient, and the background magnetic field in suchcases is not necessary, anyhow. An example of this is given in thetext. Frequencies of the IA waves from one side and plasma Langmuir (PL) and electromagnetic (EM, light) waves from the other, are well separated. The former are normally below the ion plasma frequency, while the PL and EM waves have a lower cut-off at the electron plasma frequency. While these modes are normally uncoupled within linear theory, the situation is quite different in nonlinear regimes, when IA-PL-EM waves are coupled through so-called parametric decay instability or IA-EM waves in the process called stimulated Brillouin back-scattering (Chen 1984). In contrast to this, the coupling presented in Sect. 2 is essentially linear.
-
b)
The second source of the IA wave are inflows of plasmas from some layers to other layers; examples of that kind are numerous and widespread in the atmosphere. Such phenomena create a permeating-plasma environment (Vranjes et al. 2009; Vranjes 2011c), and the presence of these macroscopic motions implies free energy that can be channeled into the excitation of IA waves. This is discussed in detail in Sect. 3.
In the solar atmosphere where the ion and electron temperatures are of the same order, the IA wave is normally expected to be strongly damped due to kinetic effects. However in the presence of an energy source that can compensate for losses due to the Landau damping, the IA wave can develop in such an environment as well. Typically this can happen in the case of electron currents when the IA wave is growing, providing that the equilibrium electron speed exceeds a certain limit. For coronal temperatures on the order of one million K, this critical electron speed is around 27cs, where cs is the sound speed. Hence, the instability threshold is rather high. However, a much lower instability threshold is required for another type of kinetic instability in which one plasma propagates through another. Such permeating plasmas are, in fact, frequently seen in the solar atmosphere, where the plasma from lower layers is accelerated towards upper layers. Those upper layers already contain a plasma (described by different parameters), so that we have perfect examples of permeating plasmas throughout the solar atmosphere. This new effect was discovered in our very recent works and applied to cometary plasmas permeated by solar/stellar winds (Vranjes 2011c). Here, it was shown to produce a dust-acoustic mode that is practically always growing. In the present work, we show that the instability is rather effective in the solar atmosphere as well.
Regardless of which of the two suggested widespread sources may be in action, the excited IA waves may be dissipated most effectively by two processes. The first one, the Landau damping mechanism, is physically purely kinetic, when the energy of the wave is transformed first into particle acceleration and then eventually into heat due to collisions. Within the IA wave excitation mechanism a) mentioned above, we present a fluid model for its Landau damping. The second process of wave energy dissipation is stochastic and again implies a wave-particle interaction that directly leads to stochastic (chaotic) motion and heating.
Regarding the second dissipation mechanism, it should be stressed that most of the plasma modes that follow from multi-component plasma theory are known to cause stochastic heating. This holds particularly for electrostatic modes like the IA wave, PL wave, lower and upper hybrid waves, ion and electron cyclotron waves, ion and electron Bernstein waves, drift waves (oblique and transverse), and standing waves in general (that can be some of those mentioned here). The electromagnetic modes, like the Alfvén wave, can also heat the plasma by the same mechanism; however as a rule the heating rate is lower and the mechanism requires large mode amplitudes. More precisely, for the Alfvén wave this implies a strongly nonlinear regime with the perturbed to equilibrium magnetic field ratio B1/B0 ≥ 0.75 (Smith & Kaufman 1975; 1978). This can be compared with the requirement for stochastic heating with IA waves, where the necessary density perturbation threshold is only n1/n0 = 0.077 (Smith & Kaufman 1975; 1978), and the heating is in fact much more efficient.
In terms of the perturbed electric field, for practically all mentioned electrostatic modes there is a critical electric field amplitude that is needed for the stochastic heating to take place. For the oblique drift (OD) wave, stochastic heating takes place if 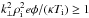 . It causes the heating of bulk plasma, heats heavier ions better than light ions, and acts mainly in the perpendicular direction. Details of this mechanism as applied to the solar corona can be found in Vranjes & Poedts (2009a,b; 2010a,b). In the case of the transverse drift (TD) wave, we have an electromagnetic mode; yet even in this case, one obtains the required amplitude of the perturbed electric field
. It causes the heating of bulk plasma, heats heavier ions better than light ions, and acts mainly in the perpendicular direction. Details of this mechanism as applied to the solar corona can be found in Vranjes & Poedts (2009a,b; 2010a,b). In the case of the transverse drift (TD) wave, we have an electromagnetic mode; yet even in this case, one obtains the required amplitude of the perturbed electric field 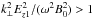 . Here, Ez1 denotes the electric field that is strictly parallel to the magnetic field; hence we have an effective acceleration of particles that is accompanied by stochastic heating in both parallel and perpendicular directions and by transport in the perpendicular direction. In this case, the heating acts on both ions and electrons; more details are available in Vranjes (2011a,b).
. Here, Ez1 denotes the electric field that is strictly parallel to the magnetic field; hence we have an effective acceleration of particles that is accompanied by stochastic heating in both parallel and perpendicular directions and by transport in the perpendicular direction. In this case, the heating acts on both ions and electrons; more details are available in Vranjes (2011a,b).
For standing waves, the necessary wave electric field is ekE/(mω2) ≈ 0.15–0.25. Details on this mechanism can be found in Hsu et al. (1979), and in Doveil (1981). All these criteria and features of stochastic heating have been verified in numerous laboratory experiments; some of the mentioned references contain experimental confirmation of the phenomenon.
2. Ion acoustic wave in an inhomogeneous environment: excitation in the presence of and coupling with the transverse electromagnetic (light) waves
2.1. Derivation of a wave equation
We assume a plasma is immersed in an external magnetic field B0 = B0ez. The magnetic field is here only in order to have a physically justified equilibrium. In the case of a density gradient in the perpendicular direction 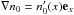 , the equilibrium yields the diamagnetic drift speed
, the equilibrium yields the diamagnetic drift speed 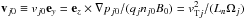 ,
, 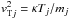 ,
, 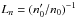 .
.
For ion perturbations with the phase speed ω/k on the order of ion thermal speed, it may be necessary to include an equation for ion temperature (energy), which may be written in the form (Weiland 2000; Vranjes et al. 2008) 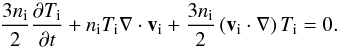 (1)For a constant equilibrium temperature, the linearized energy equation reduces to
(1)For a constant equilibrium temperature, the linearized energy equation reduces to 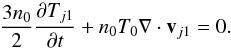 (2)We assume quasi-neutrality both in equilibrium and in perturbed state, and Tj0 = T0. The linearized momentum and continuity equations are
(2)We assume quasi-neutrality both in equilibrium and in perturbed state, and Tj0 = T0. The linearized momentum and continuity equations are 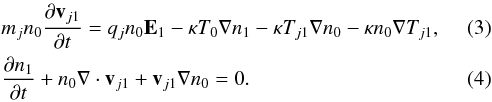 In Eq. (3) the magnetic field effect is completely neglected. The explanation for this is as follows. The assumed perturbations are due to both a longitudinal and a transverse electric field. The former is responsible for compressional perturbations that eventually lead to IA and PL perturbations. The latter (transverse) is due to the assumed presence of electromagnetic perturbations. The omitted linearized Lorentz force term yields two terms v × B ⇒ v⊥ 1 × B0 + v0 × B1. Here, v⊥ 1 is clearly only due to the transverse electric field, which has the frequency
In Eq. (3) the magnetic field effect is completely neglected. The explanation for this is as follows. The assumed perturbations are due to both a longitudinal and a transverse electric field. The former is responsible for compressional perturbations that eventually lead to IA and PL perturbations. The latter (transverse) is due to the assumed presence of electromagnetic perturbations. The omitted linearized Lorentz force term yields two terms v × B ⇒ v⊥ 1 × B0 + v0 × B1. Here, v⊥ 1 is clearly only due to the transverse electric field, which has the frequency 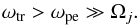 (5)This perpendicular movement changes direction many times within the hypothetical gyro-period. In other words, the perturbed perpendicular dynamics corresponds to that of an un-magnetized plasma, so that the Lorentz force is negligible and particle motion is almost without any drift features. The second contribution from the Lorentz force v0 × B1 is also negligible because the ratio of the second and first terms v0/vph, vph = ωtr/k is a small quantity.
(5)This perpendicular movement changes direction many times within the hypothetical gyro-period. In other words, the perturbed perpendicular dynamics corresponds to that of an un-magnetized plasma, so that the Lorentz force is negligible and particle motion is almost without any drift features. The second contribution from the Lorentz force v0 × B1 is also negligible because the ratio of the second and first terms v0/vph, vph = ωtr/k is a small quantity.
The remaining displacement in the perpendicular x and y directions due to the transverse time-varying electric field is well-known from books. It can easily be calculated, yielding known results: ![\begin{eqnarray*} x&=&\left[q_j E_1/\left(m\left(\omega_{\rm tr}^2-\Omega_{j}^2\right)\right)\right] \left[\cos \left(\Omega_{j} t\right) - \cos\left(\omega_{\rm tr} t\right)\right], \\ y&=&\left[q_j E_1/\left(m\left(\omega_{\rm tr}^2-\Omega_{j}^2\right)\right)\right]\left[\left(\Omega_{j}/\omega_{\rm tr}\right) \left[\sin \left(\omega_{\rm tr} t\right) - \sin \left(\Omega_{j} t\right)\right]\right.. \end{eqnarray*}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq27.png) Making a plot x(t) and y(t) confirms the assumed model as long as the condition (5) is satisfied.
Making a plot x(t) and y(t) confirms the assumed model as long as the condition (5) is satisfied.
In Eq. (4) the equilibrium diamagnetic drift contribution is exactly zero as long as the magnetic field is constant (Weiland 2000; Vranjes & Poedts 2009c). Hence, for perturbations of the shape f(x)exp( − iωt + ikz), we have from Eqs. (3), (4) 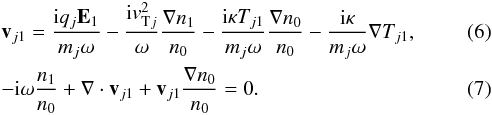 From Eq. (2) the perturbed temperature is
From Eq. (2) the perturbed temperature is 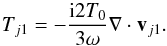 (8)Now we calculate ∇·vj1 and use it in Eqs. (7), (8). This yields
(8)Now we calculate ∇·vj1 and use it in Eqs. (7), (8). This yields 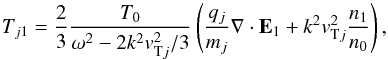 (9)and we have the number density expressed through the perturbed electric field
(9)and we have the number density expressed through the perturbed electric field ![\begin{eqnarray} n_1&=&\frac{q_j n_0}{m_{j} \omega_{j}^2}\left(1+ \delta_{j2}\right) \nabla\cdot\vec E_1 + \frac{q_j \vec E_1}{m_{j} \omega_{j}^2} \nabla n_0, \label{e5} \\[2mm]\nonumber \omega_{j}^2&\equiv& \omega^2 - k^2 \vtj^2 - \delta_{j1}, \quad \delta_{j1}= \delta_{j3} k^4 \vtj^4, \quad \delta_{j2}= \delta_{j3} k^2 \vtj^2, \\[2mm] \nonumber\delta_{j3}&=& \frac{2}{3}\frac{1}{\omega^2- 2 k^2 \vtj^2/3}\cdot \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq35.png) (10)In derivations we used the assumption of local approximation and small equilibrium gradients. Thus, we neglected the second-order derivative of the equilibrium density gradient, as well as products of first derivatives, and used the fact that k ⊥ ∇n0. The terms δj1,2,3 originate from temperature perturbations. Hence, setting them equal to zero (see later in the text) is equivalent to reducing derivations to isothermal case.
(10)In derivations we used the assumption of local approximation and small equilibrium gradients. Thus, we neglected the second-order derivative of the equilibrium density gradient, as well as products of first derivatives, and used the fact that k ⊥ ∇n0. The terms δj1,2,3 originate from temperature perturbations. Hence, setting them equal to zero (see later in the text) is equivalent to reducing derivations to isothermal case.
The purpose of the derivation performed so far is to calculate the current that appears in the general wave equation, 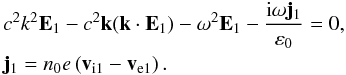 (11)Using Eq. (10) we may express Tj1 in Eq. (9) through the electric field only. We then calculate ∇Tj1 and ∇n1, and with all this from Eq. (6) we finally obtain the perturbed velocity expressed through the perturbed electric field and equilibrium density gradient:
(11)Using Eq. (10) we may express Tj1 in Eq. (9) through the electric field only. We then calculate ∇Tj1 and ∇n1, and with all this from Eq. (6) we finally obtain the perturbed velocity expressed through the perturbed electric field and equilibrium density gradient: ![\begin{eqnarray} \nonumber &&\vec v_{j1}\!=\!\frac{{\rm i} q_j \vec E_1}{m_{j} \omega} - \frac{{\rm i} q_j \vtj^2}{m_{j} \omega}\!\left\{\!\frac{1+ \delta_{j2}}{\omega_{j}^2} + \delta_{j3} \left[\!1+ \frac{k^2\vtj^2}{\omega_{j}^2} (1+ \delta_{j2})\! \right]\right\}\! \nabla \!\left( \nabla\!\cdot\! \vec E_1\!\right) \\[2mm]\nonumber &&-\frac{{\rm i} q_j \vtj^2}{m_{j} \omega}\frac{\nabla n_0}{n_0} \left\{\frac{1+ \delta_{j2}}{\omega_{j}^2} + \delta_{j3} \left[1+ \frac{k^2\vtj^2}{\omega_{j}^2} (1+ \delta_{j2}) \right] \right\} \nabla\!\cdot\!\vec E_1 \\[2mm] &&-\frac{{\rm i} q_j \vtj^2}{m_{j} \omega}\frac{n_0'}{n_0} \frac{1}{\omega_{j}^2} \left(1+ \delta_{j3} k^2 \vtj^2\right) \nabla E_{1x}. \label{e7} \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq42.png) (12)Using this in Eq. (11) yields the wave equation with the perturbed electric field only.
(12)Using this in Eq. (11) yields the wave equation with the perturbed electric field only.
2.1.1. Isothermal perturbations and cold ion case
We are interested in showing some features and effects of coupling between the IA and EM transverse (i.e., light) waves. In view of very lengthy expressions, analytically this is most clearly done in the limit of cold ions and for isothermal electron perturbations. For this purpose we take δj = 0, and after setting Eq. (12) into the wave Eq. (11) we obtain ![\begin{eqnarray} \nonumber &&c^2 k^2 \vec E_1 - c^2 \vec k \left(\vec k\!\cdot \! \vec E_1\right)- \omega^2 \vec E_1 + \left(\!\omega_{\rm pe}^2 \!+ \omega_{\rm pi}^2\!\right) \vec E_1 -\frac{\omega_{\rm pe}^2 \vte^2}{\omega_{\rm e}^2}\frac{n_0'}{n_0} \nabla E_{1x} \\[2mm] &&- \frac{\omega_{\rm pe}^2\vte^2}{\omega_{\rm e}^2} \nabla\left(\nabla\!\cdot \!\vec E_1\right) -\frac{\omega_{\rm pe}^2 \vte^2}{\omega_{\rm e}^2} \frac{\nabla n_0}{n_0} \nabla\cdot \vec E_1=0, \label{e8} \\[2mm]\nonumber &&\omega_{\rm e}^2=\omega^2-k^2\vte^2. \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq44.png) (13)The y-component of this vector equation yields one light wave decoupled from the rest
(13)The y-component of this vector equation yields one light wave decoupled from the rest 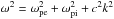 . However, the z and x components yield the longitudinal electrostatic (IA plus PL) waves, as well as another light transverse wave, coupled through the equilibrium density gradient
. However, the z and x components yield the longitudinal electrostatic (IA plus PL) waves, as well as another light transverse wave, coupled through the equilibrium density gradient ![\begin{eqnarray} &&\label{e9}\left( - \omega^2 + \omega_{\rm pe}^2 + \omega_{\rm pi}^2 + \frac{k^2 \vte^2 \omega_{\rm pe}^2}{\omega_{\rm e}^2}\right)E_{1z}-\frac{{\rm i} k \omega_{\rm pe}^2\vte^2}{\omega_{\rm e}^2}\frac{n_0'}{n_0} E_{1x}=0, ~~~~~~~~~\\[2mm] &&\label{e10}\left( - \omega^2 + \omega_{\rm pe}^2 + \omega_{\rm pi}^2 + k^2 c^2\right)E_{1x}- \frac{{\rm i} k \omega_{\rm pe}^2\vte^2}{\omega_{\rm e}^2}\frac{n_0'}{n_0} E_{1z}=0. \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq47.png) Equation (14) describes longitudinal electric field E1z and corresponding wave oscillations coupled to the transverse electromagnetic wave E1x in the presence of the given density gradient.
Equation (14) describes longitudinal electric field E1z and corresponding wave oscillations coupled to the transverse electromagnetic wave E1x in the presence of the given density gradient.
The mechanism of excitation of the IA wave in the inhomogeneous environment, which simultaneously contains EM waves, and its coupling with the latter can be understood by comparing the cases without and with the density gradient, see Fig. 1.
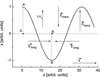 |
Fig. 1 Mechanism of excitation of the longitudinal electrostatic field Elong ≡ Ez in the presence of a transverse wave with electric field in x direction, which propagates in z-direction. |
We first see details of the case with density gradient in x-direction. For this we may focus on one layer with certain density n0 at the position x0. Obviously, this density is initially the same for any point in z-direction that has the same position x0. In this layer we may choose two fixed arbitrary points, A(x0,z1) and B(x0,z2), at two different positions in z-direction. Due to the E1x field, the plasma in this layer will be displaced in x-direction in such a way as to follow a sinusoidal profile in z-direction. The sinusoidal line in Fig. 1 represents a displacement of a layer that was initially at x = 0, caused by the transverse electric field Etrans ≡ Ex. This will have two consequences: i) the densities n(x0,z1), n(x0,z2) at the points A(x0,z1) and B(x0,z2) will no longer be the same; ii) in addition, because of the opposite motion of electrons and ions due to the transverse electric field in x-direction, there will be an excess of charge of one or another sign at every point for any z, and this holds for the points A(x0,z1) and B(x0,z2) as well. The reason for this is clear: when one species (e.g., ions) moves from an arbitrary point (let it be A) along x, it is replaced by particles of the same species that come from some other point in x direction, which has different (e.g., smaller) density. On the other hand, electrons from this same point move in the opposite direction and are replaced by electrons that come from the opposite side, as compared to moving ions. So there will be more electrons in the point A. Something similar happens at the point B. From i) and ii) it follows that there will be a difference of charge in the chosen arbitrary points A(x0,z1) and B(x0,z2). This further implies that there will be an additional electric field E1z in the z direction. This excited longitudinal electric field will be accompanied by corresponding density oscillations, and this will result in IA and Langmuir waves. This all is depicted in Fig. 1, where x0 = 0. In view of the mass difference, electrons are expected to play the main role in the excitation of the longitudinal electric field.
From the presented model, it is also clear that the equilibrium magnetic field plays no role in the process, as we explained earlier. This is because the frequency of the transverse oscillations is much higher than the particle gyro-frequency, that is, the particle is unmagnetized. This is in agreement with the standard theory of transverse light waves, which in the high-frequency range predicts the same behavior of the EM wave in plasmas with or without a background magnetic field (Chen 1984; Bellan 2006). The only essential ingredients are therefore the transverse oscillating electric field and the density gradient in the same direction.
If we now focus on the case without density gradient, it becomes clear that the effects described above vanish. There is no electric field in z-direction because density is constant everywhere.
The process described above will be quantified and confirmed by using realistic parameters for laboratory and solar plasmas, both isothermal and non-isothermal.
The dispersion relation that follows from Eqs. (14), (15) reads ![\begin{eqnarray} \nonumber &&\left(\omega^2- k^2 \vte^2\right) \left[ \omega^2 \left(\omega_{\rm pe}^2 + \omega_{\rm pi}^2 - \omega^2\right) + k^2\vte^2\left(\omega^2- \omega_{\rm pi}^2\right)\right] \\[2mm] &&\times \left(\omega_{\rm pe}^2 + \omega_{\rm pi}^2 + c^2 k^2- \omega^2\right) +\frac{k^2 \omega_{\rm pe}^4 \vte^4}{L_n^2}=0. \label{e11} \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq62.png) (16)The last term in Eq. (16) describes the coupling of EM transverse waves from one side and IA and Langmuir waves from the other. Without this term, the transverse and longitudinal waves propagate without interaction. In the IA frequency range
(16)The last term in Eq. (16) describes the coupling of EM transverse waves from one side and IA and Langmuir waves from the other. Without this term, the transverse and longitudinal waves propagate without interaction. In the IA frequency range 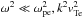 , Eq. (16) yields the modified IA mode
, Eq. (16) yields the modified IA mode 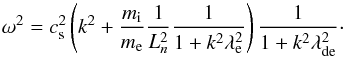 (17)Here, λe = c/ωpe, λde = vTe/ωpe. It is seen that in the limit of small k, the IA wave coupled with the transverse wave in the presence of the density gradient has some cut-off frequency ωc, which goes toward
(17)Here, λe = c/ωpe, λde = vTe/ωpe. It is seen that in the limit of small k, the IA wave coupled with the transverse wave in the presence of the density gradient has some cut-off frequency ωc, which goes toward 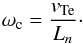 (18)In addition, it turns out that the wave group speed may become negative, that is, the wave becomes backward and the dispersion curve for the IA wave may have a trough in the profile. A simple condition describing such a situation can be derived by neglecting
(18)In addition, it turns out that the wave group speed may become negative, that is, the wave becomes backward and the dispersion curve for the IA wave may have a trough in the profile. A simple condition describing such a situation can be derived by neglecting 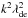 with respect to unity. This yields ∂ω/∂k < 0, provided that
with respect to unity. This yields ∂ω/∂k < 0, provided that 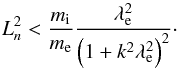 (19)For realistic parameters in laboratory plasmas, this condition may easily be satisfied. In space plasmas this is far less likely because it implies small values for the density scale length Ln that are certainly possible but are not expected to last long enough so that a wide-spread excitation of IA waves takes place within the life time of such density gradients. However, the cut-off (18) remains as a feature for any plasma.
(19)For realistic parameters in laboratory plasmas, this condition may easily be satisfied. In space plasmas this is far less likely because it implies small values for the density scale length Ln that are certainly possible but are not expected to last long enough so that a wide-spread excitation of IA waves takes place within the life time of such density gradients. However, the cut-off (18) remains as a feature for any plasma.
To demonstrate the possibility of a backward mode, as an example, Eq. (16) is solved numerically for the laboratory plasma taking cold ions and Ln = 0.1 m, Te = 104 K, n0 = 1018 m-3. The result for the IA mode is presented in Fig. 2. It is seen that the mode has backward features for small k and it has a cut-off; all this is in agreement with Eqs. (17)–(19).
Here and in Sects. 2.1.2, 2.2, 2.3, we present IA waves only, because the properties of this mode are changed due to coupling. However, it should be kept in mind that the same mechanism of excitation applies to the Langmuir wave as well, though the features of this mode remain almost the same as in the case without coupling. But the energy of both excited waves (IA and Langmuir) is eventually transformed into heat by the same Landau damping effect.
2.1.2. Perturbations in plasmas with hot ions
In the IA wave frequency range, the electrons may be taken as isothermal because vTe ≫ ω/k = vph (see more in Stix 1992; and in Bellan 2006). This considerably simplifies equations without losing any important physical effect. Thus, we set δe1,2,3 = 0 and repeat the procedure as above for hot ions, and for their temperature variation described by Eq. (2). Using Eq. (12) with δi1,2,3 ≠ 0 this yields the following wave equation
![$$ -\left\{\!\omega_{\rm pi}^2\vti^2 \left[\! \frac{1+ \delta_{\rm i2}}{\omega_{\rm i}^2} + \delta_{\rm i3} \left(\! 1+ \frac{k^2\vti^2}{\omega_{\rm i}^2} (1+ \delta_{\rm i2}) \!\right)\!\right] + \frac{\omega_{\rm pe}^2 \vte^2}{\omega_{\rm e}^2}\!\right\}\! \frac{\nabla n_0}{n_0} \nabla\!\cdot\! \vec E_1 $$](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq83.png)
![\begin{equation} - \left[\frac{\omega_{\rm pi}^2 \vti^2}{\omega_{\rm i}^2} \left(1+ \delta_{\rm i3} k^2 \vti^2\right) + \frac{\omega_{\rm pe}^2 \vte^2}{\omega_{\rm e}^2}\right]\frac{n_0'}{n_0}\nabla E_{1x}=0. \label{e11a} \end{equation}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq84.png) (20)The y-component again yields one electromagnetic wave, and from the x,z-components we obtain the following dispersion equation that describes longitudinal IA and Langmuir waves coupled to another electromagnetic transverse wave with the electric field in x-direction:
(20)The y-component again yields one electromagnetic wave, and from the x,z-components we obtain the following dispersion equation that describes longitudinal IA and Langmuir waves coupled to another electromagnetic transverse wave with the electric field in x-direction:
 |
Fig. 2 Numerical solution of Eq. (16) for the IA wave in laboratory plasma with backward features and cut-off, both caused by interaction with transverse light wave in the presence of density gradient. |
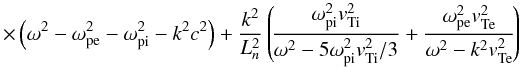
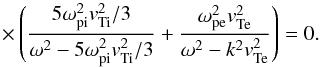 (21)In the cold ion limit, this equation reduces to Eq. (16). Equation (21) can be solved numerically for coronal plasma, and for this purpose we take parameters T = 106 K, n = 1015 m-3, and Ln = 105 m. We note that for these parameters and assuming the magnetic field 10-2 T, we have ωpi/Ωi = 43; thus the frequency of the transverse wave is indeed far above the gyro-frequency, and the perpendicular dynamics of particles fits into the unmagnetized plasma model described previously in the text.
(21)In the cold ion limit, this equation reduces to Eq. (16). Equation (21) can be solved numerically for coronal plasma, and for this purpose we take parameters T = 106 K, n = 1015 m-3, and Ln = 105 m. We note that for these parameters and assuming the magnetic field 10-2 T, we have ωpi/Ωi = 43; thus the frequency of the transverse wave is indeed far above the gyro-frequency, and the perpendicular dynamics of particles fits into the unmagnetized plasma model described previously in the text.
The frequency of the IA wave excited in the presence of the light wave and the density gradient is presented in Fig. 3 (full line), together with a straight (dashed) line that describes the frequency of the usual IA wave in homogeneous plasma that goes to zero for k → 0. The cut-off defined by Eq. (18) in the present case yields a frequency around ≃40 Hz. We observe that this is orders of magnitude greater than the cut-off induced by gravity (Vranjes 2011d), which is around 10-3 Hz.
 |
Fig. 3 Numerical solution of Eq. (21) for IA wave in solar atmosphere. Line a: the usual IA wave in plasma with hot coronal ions. Line b: the IA wave propagating in the presence of the transverse light wave in plasma with density gradient. |
2.2. Ion Landau damping versus excitation in the presence of transverse wave
Longitudinal electrostatic IA perturbations are known to be subject to Landau damping, within which the energy of wave motion is dissipated and transformed into thermal energy of particles. This opens up a possibility for precipitation of energy from light waves into heating. This mechanism is expected to work best in magnetic structures where radial density gradients appear as natural features simply due to balance of forces (while the background magnetic field plays no further role for the wave excitation), so the presented new IA wave excitation may be ubiquitous there. Landau damping is the most important ion thermal effect and is a purely kinetic phenomenon. However, there exists a way to include it even within the fluid theory using the method suggested several decades ago by D’Angelo et al. (1979). The model implies that in the linearized ion momentum equation a dissipative term of the shape 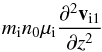 (22)is added in such a way as to describe well-known experimentally verified features of kinetic Landau damping (Sessler & Pearson 1967; Andersen et al. 1968) The reason for such a choice and the properties of the coefficient μi are described in Appendix A. It is interesting to point out that with an appropriate choice of μi the ion kinetic effects can in fact be described more accurately than by using kinetic theory in standard approximate way, that is, by expanding the plasma dispersion function; see more details on this issue in Appendix A.
(22)is added in such a way as to describe well-known experimentally verified features of kinetic Landau damping (Sessler & Pearson 1967; Andersen et al. 1968) The reason for such a choice and the properties of the coefficient μi are described in Appendix A. It is interesting to point out that with an appropriate choice of μi the ion kinetic effects can in fact be described more accurately than by using kinetic theory in standard approximate way, that is, by expanding the plasma dispersion function; see more details on this issue in Appendix A.
To describe such a Landau damping model in the most transparent way, we assume isothermal but hot ions; their momentum equation in this case yields
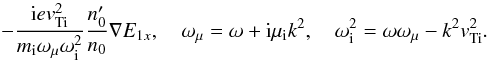 The isothermal electron speed is obtained from Eq. (12) by setting δe1,2,3 = 0. The derivations are repeated in the same manner as in Sect. 2.1.1, which yields the following dispersion equation for the x,z components of the electric field:
The isothermal electron speed is obtained from Eq. (12) by setting δe1,2,3 = 0. The derivations are repeated in the same manner as in Sect. 2.1.1, which yields the following dispersion equation for the x,z components of the electric field: ![\begin{eqnarray} \nonumber &&\left(\omega^2 - \omega_{\rm pe}^2 - \omega_{\rm pi}^2\frac{\omega}{\omega_{\mu}} - \alpha k^2 \right)\! \left(\omega^2 - \omega_{\rm pe}^2 - \omega_{\rm pi}^2 \frac{\omega}{\omega_{\mu}} - c^2 k^2\right) \\[2mm] &&+ \frac{k^2 \alpha^2}{L_n^2}\! =\! 0, \label{ld2} \\[2mm] &&\alpha= \frac{\omega}{\omega_{\mu}} \frac{ \omega_{\rm pi}^2 \vti^2}{\omega \omega_{\mu} - k^2\vti^2} + \frac{\omega_{\rm pe}^2 \vte^2}{\omega^2- k^2 \vte^2}\cdot \nonumber \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq102.png) (23)Dispersion Eq. (23) contains all relevant ion thermal effects, including Landau damping through the term μi in ωμ, and it will be solved numerically using the expressions for μi from Appendix A.2.
(23)Dispersion Eq. (23) contains all relevant ion thermal effects, including Landau damping through the term μi in ωμ, and it will be solved numerically using the expressions for μi from Appendix A.2.
 |
Fig. 4 Numerical solution of Eq. (23) for the IA wave spectrum. Dashed lines: the frequency (line a1) and absolute value of Landau damping (line a2) of the IA wave for homogeneous plasma with hot coronal ions. Full lines: the frequency (line b1) and damping (line b2) of the IA wave excited in the presence of the transverse light wave in inhomogeneous plasma. |
The result is presented in Fig. 4 for the same parameters as in Fig. 3. Lines b1 and b2 give, respectively, the frequency and Landau damping for the IA wave that propagates in the presence of light waves in plasma with density gradient. For comparison, the dashed lines a1, a2 give the corresponding frequency and Landau damping for homogeneous plasma with the same parameters. We observe that the Landau damping given by line b2 in inhomogeneous plasma is reduced and is much smaller than the frequency, in particular for small values of k, contrary to the homogeneous plasma, where frequency and damping become of the same order for small k, as seen from lines a1, a2.
The explanation for this is as follows. The Landau effect is most effective in cases when the wave phase speed ω/k is close to the thermal speed of the bulk ions. However, it can be seen from Figs. 2–4 that for the IA wave excited in the presence of the light wave the frequency for small k is much higher (because of the cut-off effect) than the frequency of the normal IA wave kcs in homogeneous plasmas. This implies that in the given range of short k the phase speed is in fact shifted far from the thermal speed, that is, toward the tail of the ion distribution. Consequently, a considerably smaller number of ions will satisfy the resonant condition, and the Landau damping must be strongly reduced. These fine features are seen in Fig. 4; for example, at k ≃ 1.6 (in given units) from lines b1, b2 we have ω ≃ 41 Hz, γ = −0.84 Hz, so |γ/ω| = 0.02, while from lines a1, a2 we have ω ≃ 12, γ ≃ 8, so that |γ/ω| = 0.67. The ratio is more than 33 times smaller in the first case!
It may be concluded that the light waves not only help the excitation of the IA waves in inhomogeneous environment but also drastically reduce the Landau damping of these excited IA waves.
2.3. Plasma with both temperature and density gradients
Derivations from Sect. 2 can be repeated for plasmas that are kept in equilibrium by oppositely oriented density and temperature gradients (Vranjes et al. 2007): 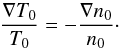 (24)The equations become very lengthy for hot ions and non-isothermal perturbations, and yet no new physical effects appear in comparison with much more simple isothermal derivations with cold ions. The latter yield the wave equation
(24)The equations become very lengthy for hot ions and non-isothermal perturbations, and yet no new physical effects appear in comparison with much more simple isothermal derivations with cold ions. The latter yield the wave equation ![\begin{eqnarray} \nonumber &&c^2 k^2 \vec E_1 - c^2 \vec k \left(\vec k\cdot \vec E_1\right)- \omega^2 \vec E_1 + \left(\omega_{\rm pe}^2 + \omega_{\rm pi}^2\right) \vec E_1 - \frac{\omega_{\rm pe}^2}{L_n} \frac{\vte^2}{\omega_{\rm e}^2} \nabla E_{1x} \\[2mm] &&+\frac{\omega_{\rm pe}^2k^2 \vte^4}{\omega_{\rm e}^4} \frac{\vec e_x}{L_n} \nabla\cdot \vec E_1 - \frac{\omega_{\rm pe}^2\vte^2}{\omega_{\rm e}^2} \nabla\left(\nabla\cdot \vec E_1\right)=0, \label{t2} \\[2mm] && \omega_{\rm e}^2\!=\!\omega^2\!-\!k^2\vte^2. \nonumber \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq113.png) (25)This yields the following dispersion equation for coupled longitudinal and light waves:
(25)This yields the following dispersion equation for coupled longitudinal and light waves: ![\begin{eqnarray} \nonumber &&\left(\omega^2- k^2 \vte^2\right)^2 \left[ \omega^2 \left(\omega_{\rm pe}^2 + \omega_{\rm pi}^2 - \omega^2\right) + k^2\vte^2\left( \omega^2- \omega_{\rm pi}^2 \right)\right] \\[2mm] &&\times \left(\omega_{\rm pe}^2 + \omega_{\rm pi}^2 + c^2 k^2- \omega^2\right) =\frac{k^4 \omega_{\rm pe}^4 \vte^6}{L_n^2}\cdot \label{t3} \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq114.png) (26)Equation (26) is slightly different than Eq. (16); however, in the IA frequency range it yields the same dispersion Eq. (17) as before.
(26)Equation (26) is slightly different than Eq. (16); however, in the IA frequency range it yields the same dispersion Eq. (17) as before.
Consequently, the IA wave excitation in the presence of the light wave remains similar even for a rather different equilibrium (24). The physics of coupling will not change by including hot ion effects. The presented mechanism of excitation can thus act in various geometries, with or without the external magnetic field.
2.4. Refraction and focusing of transverse wave by background density gradient: accumulation of wave energy in regions with lower density
In a less ideal picture, the oscillating electromagnetic field may in fact have electric field at an arbitrary angle with respect to the density gradient. Nevertheless, the mechanism described in Fig. 1 will work as long as this electric field is not strictly orthogonal to ∇n0. This implies that in real situations the described coupling between transverse and longitudinal waves may be widespread because electromagnetic waves are indeed omnipresent and propagate in any direction independently of the magnetic field geometry.
On the other hand, the phase speed of the transverse wave is greater than the speed of light 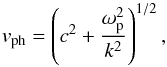 (27)which implies that the coupling with IA perturbations may take place practically instantaneously along large sections of a magnetic flux tube through which the EM wave propagates.
(27)which implies that the coupling with IA perturbations may take place practically instantaneously along large sections of a magnetic flux tube through which the EM wave propagates.
From the given phase speed, it is also seen that a wave with a certain frequency propagates faster in a more dense environment. In a magnetic flux tube, due to pressure balance, one may expect reduced density inside the tube and enhanced at the edge. The refraction index of the transverse wave is N = c/vph < 1, so that the wave front initially propagating along such a magnetic flux tube will bend and there will be refraction and focusing of the wave towards the center of the tube cylinder. This also implies that the direction of the wave electric field will continuously change its angle with respect to the magnetic field vector, but the excitation of the IA wave will still be taking place as explained earlier. This refraction and focusing of the EM wave is depicted in Fig. 5, where the wave initially propagates along the magnetic field and has an electric field vector in the direction of the background density gradient. The wave front becomes distorted, so that the wave is directed towards the region of lower plasma density.
 |
Fig. 5 Refraction and focusing of transverse electromagnetic wave with the wave number k in plasma with density gradient. |
The consequences of this effect may be numerous. In laboratory situations this effect is used for plasma heating by CO2 lasers (Chen 1984); an elongated plasma with lower density on the axis acts as a lens, and the radiation converges towards the axis and becomes trapped inside the plasma. The same lens effect is behind radio communications around the globe; in this case waves are reflected from ionospheric layers and are therefore able to travel around the globe.
A similar physical mechanism is behind well-known self-focusing of strong electromagnetic beams. In this case the nonlinear ponderomotive force pushes plasma out of the beam and the phase speed inside the beam is smaller compared to the outer region; as a result the beam becomes focused.
The principles of linear fusion reactor (i.e., plasma heating) described above, which are known and used in rather unfavorable conditions in typical laboratory plasmas, may naturally be in action in very elongated magnetic flux tubes in the solar corona, where conditions for such a heating are much more favorable. Hence, such a focused electromagnetic transverse wave will more effectively support excitation of the IA waves by the mechanism described previously in the text and can also heat inner regions of magnetic flux tubes through the nonlinear wave coupling mentioned in Sect. 1.
Such mechanisms, although well explored and used in practice in laboratory plasmas, have not been studied in the problem of coronal heating. Focused EM or light waves imply larger wave amplitudes inside a region of less dense plasma (e.g., in a flux tube), and in such circumstances nonlinear effects may become important, like the parametric decay instability mentioned in Sect. 1. In this case the EM wave energy is converted into plasma wave energy and the latter is then transferred directly to electrons through Landau damping. This mechanism is standardly used in laser fusion experiments, for example in iodine laser heating. The required EM wave amplitude for this phenomenon is known (Bellan 2006), and it reads 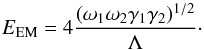 (28)Here, Λ is the nonlinear coupling coefficient
(28)Here, Λ is the nonlinear coupling coefficient
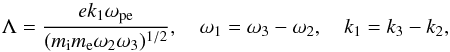 where indices 1,2,3 refer to IA, PL, and EM waves, respectively, and γ1,γ2 are linear damping rates for IA and PL modes, which in application to coronal plasmas are just the usual Landau damping rates.
where indices 1,2,3 refer to IA, PL, and EM waves, respectively, and γ1,γ2 are linear damping rates for IA and PL modes, which in application to coronal plasmas are just the usual Landau damping rates.
Very similar is nonlinear excitation of IA waves through so-called parametric backscattering instability, which involves an EM pump wave that excites one IA wave and another EM one moving in the opposite direction. This requires an EM pump wave amplitude that is same as above (28), but with the slightly different coupling constant
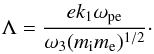 In this case the IA damping rate is the same as above, while for the EM wave (which suffers no Landau damping) the damping can only be due to electron-ion collisions (typically on the order of 1 Hz, Vranjes & Poedts 2006); it reads
In this case the IA damping rate is the same as above, while for the EM wave (which suffers no Landau damping) the damping can only be due to electron-ion collisions (typically on the order of 1 Hz, Vranjes & Poedts 2006); it reads 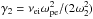 (Chen 1984). So this nonlinear coupling is accompanied by possible energy channeling into IA waves and further with ion heating due to the Landau effect.
(Chen 1984). So this nonlinear coupling is accompanied by possible energy channeling into IA waves and further with ion heating due to the Landau effect.
This shows that the IA wave is excited in both linear and nonlinear regimes. In the linear regime, the EM wave introduces a triggering mechanism only by producing a perturbed longitudinal electric field due to the density gradient. In other words, it acts as a catalyst. In both cases, it is due to the density gradient. In the linear regime this is in the region of density gradient (e.g., mainly in the outer region of a magnetic tube), while in the nonlinear regime this is the central region of the tube on which the EM wave is focused due to the same density gradient.
3. Growing ion acoustic wave in solar corona
3.1. Instability in permeating plasmas
Details of the mechanism b) introduced in Sect. 1 are described in Vranjes et al. (2009) and Vranjes (2011c). This is a kinetic derivation within which the plasma distribution function for the species j is used in the form ![\begin{equation} f_{j0}=\frac{n_{j0}}{(2\pi)^{3/2}\vtj^3} \exp\left\{-\frac{1}{2 \vtj^2}\left[v_x^2 + v_y^2 + (v_z- v_{j0})^2\right]\right\}, \label{k4} \end{equation}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq127.png) (29)where nj0 = const., vj0 is an equilibrium speed. This is used in the linearized Boltzmann kinetic equation considering two plasmas, one static and one inflowing from some other region; they are denoted with superscripts s and f, respectively. The quasi-neutrality conditions in the equilibrium are naturally satisfied in both plasmas separately:
(29)where nj0 = const., vj0 is an equilibrium speed. This is used in the linearized Boltzmann kinetic equation considering two plasmas, one static and one inflowing from some other region; they are denoted with superscripts s and f, respectively. The quasi-neutrality conditions in the equilibrium are naturally satisfied in both plasmas separately:  (30)and we shall study longitudinal electrostatic perturbations of the shape ~exp( − iω + ikz). Here, the direction z is arbitrary and in principle should not be identified with the magnetic field direction, as in the previous sections. Using Ampère’s law after a few straightforward steps, we obtain the dispersion equation for the IA wave (Vranjes et al. 2009; Vranjes 2011c):
(30)and we shall study longitudinal electrostatic perturbations of the shape ~exp( − iω + ikz). Here, the direction z is arbitrary and in principle should not be identified with the magnetic field direction, as in the previous sections. Using Ampère’s law after a few straightforward steps, we obtain the dispersion equation for the IA wave (Vranjes et al. 2009; Vranjes 2011c):
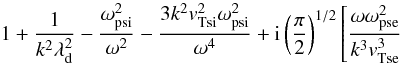
![\begin{equation} \left. + (\omega- k v_{\rm f0})\!\left(\frac{\omega_{\rm pfe}^2}{k^3 \vtfe^3} + \frac{\omega_{\rm pfi}^2}{k^3 \vtfi^3}\!\right) + \frac{\omega\omega_{\rm psi}^2 }{k^3 \vtsi^3}\! \exp\left(\!- \frac{\omega^2}{2 k^2 \vtsi^2}\right)\!\right]\!=\!0. \label{k8} \end{equation}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq136.png) (31)In the derivation of Eq. (31) the following limits are used
(31)In the derivation of Eq. (31) the following limits are used 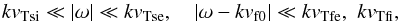 (32)where the notation is as follows:
(32)where the notation is as follows: 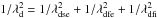 , λdse = vTse/ωpse etc., and
, λdse = vTse/ωpse etc., and 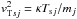 ,
, 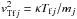 .
.
To demonstrate the instability (growing) of the IA wave, we take the following set of parameters: the temperature of all species is set to 106 K, and the number density for all species is taken as n0 = 1013 m-3. Such a choice is taken only to formally and easily satisfy the conditions (32) used for the expansions performed above, which yielded the dispersion Eq. (31). Clearly, any other combinations of the temperatures and number densities are possible. However, to remain self-consistent this would imply solving the general dispersion equation (given in Vranjes et al. 2009; Vranjes 2011c) instead of Eq. (31). This general one contains complex functions of complex arguments, and such a task could only be done numerically.
If in addition we take a relatively weak magnetic field B0 = 5 × 10-4 T, for the assumed parameters, we have the gyro-frequency and the gyro-radius for protons Ωi ≃ 48 kHz, ρi ≃ 1.9 m. Hence, we may search for the IA mode with frequency above Ωi, which will therefore be able to propagate at almost any angle with respect to the magnetic field, and the magnetic field will not affect the dynamics of ions. We note that this is not essential for the IA wave instability that is demonstrated below, but it may be of importance for associated stochastic heating (see Sect. 3.2) towards which this instability will eventually lead.
For waves propagating parallel to the magnetic field vector, the particles will not feel the magnetic field effect anyhow. In this case the dispersion Eq. (31) is solved first in terms of the wavelength, and the result is presented in Fig. 6 for the speed of the flowing plasma vf0 = 1.9cs. The figure shows a growing (unstable) mode. This is a remarkable result because the IA mode is believed to be mostly impossible to excite in plasmas with hot ions. In the present case the source of the instability is the energy stored in the flowing plasma.
An equally remarkable feature is a rather low instability threshold, which is more than one order of magnitude lower than the threshold for the electron-current-driven IA wave instability mentioned in Sect. 1. We also observe that this instability in permeating plasmas is essentially currentless, so there is no problem of consistency related to assumed homogeneity of the magnetic field as in the case of current-carrying plasma.
The transition from the usual Landau damping to growth is demonstrated in Fig. 7, where the wavelength is fixed to λ = 2 m (cf. Fig. 6) and the speed of the flowing plasma is allowed to change. The mode becomes growing at around vf0/cs = 1.7. For the parameters used here, this implies a flowing plasma speed of around 150 km s-1, which is, for example, far below the solar wind speed. Hence, the IA wave can become unstable (growing) even in an environment with hot ions like the solar corona, where it is typically expected to be strongly damped.
 |
Fig. 6 Growing IA wave in permeating coronal plasmas with the speed of the flowing quasi-neutral plasma with respect to the static plasma vf0 = 1.9cs. |
For an oblique propagation at an angle θ with respect to the magnetic field, following derivations in Alexandrov et al. (1984), it turns out that the dispersion equation does not change much. For unmagnetized ions this is self-evident and for electrons the explanation is as follows. The longitudinal electron permitivity includes the summation
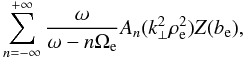 where be = (ω − nΩe)/(kzvTe), An(η) ≡ e− ηIn(η), In(η) are the Bessel functions of the second kind, and ω may include the Doppler shift as above. We point out kz in these expressions instead of k as compared with Eq. (31). In the limit | (ω − nΩe)/(kzvTe) | ≪ 1, the appropriate expansion for Z(be) is used; as a result the term containing the frequencies vanishes, while at the same time the summation becomes ∑ nAn(η) = 1. The terms driving the instability in Eq. (31) are of the form 1 − kvf0/vph, where vph = ω/k, while now for the oblique propagation k becomes kz and the whole term turns out to be replaced with
where be = (ω − nΩe)/(kzvTe), An(η) ≡ e− ηIn(η), In(η) are the Bessel functions of the second kind, and ω may include the Doppler shift as above. We point out kz in these expressions instead of k as compared with Eq. (31). In the limit | (ω − nΩe)/(kzvTe) | ≪ 1, the appropriate expansion for Z(be) is used; as a result the term containing the frequencies vanishes, while at the same time the summation becomes ∑ nAn(η) = 1. The terms driving the instability in Eq. (31) are of the form 1 − kvf0/vph, where vph = ω/k, while now for the oblique propagation k becomes kz and the whole term turns out to be replaced with 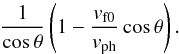 (33)Thus, for a not so large angle of propagation the instability features of the mode presented in Figs. 6, 7 will not substantially change in the case of oblique propagation, while the heating becomes more effective (Smith & Kaufman 1975, 1978). Taking the angle of propagation of 30 degrees, in view of (33) the growth rate will be increased by a factor 1.16.
(33)Thus, for a not so large angle of propagation the instability features of the mode presented in Figs. 6, 7 will not substantially change in the case of oblique propagation, while the heating becomes more effective (Smith & Kaufman 1975, 1978). Taking the angle of propagation of 30 degrees, in view of (33) the growth rate will be increased by a factor 1.16.
 |
Fig. 7 Transition from damped to growing IA mode in permeating solar plasmas for λ = 2 m. |
3.2. Stochastic heating by the ion acoustic wave
The theory presented in Sect. 3.1 is suitable for stochastic heating, whose features are as follows. In the case of a particle moving in the field of a sinusoidal wave that propagates at an angle with respect to the magnetic field vector B0 = B0ez, the resonance appears if 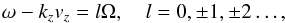 (34)where vz is the particle speed in the direction of the magnetic field. Represented in the phase space vz,z, the resonances have a narrow width if the wave amplitude is infinitesimal; there can be no overlapping in that case. For larger wave amplitudes, overlapping of resonances may take place; therefore the particle may satisfy two resonant conditions at the same time and its motion becomes random (stochastic), with its energy increased in the process.
(34)where vz is the particle speed in the direction of the magnetic field. Represented in the phase space vz,z, the resonances have a narrow width if the wave amplitude is infinitesimal; there can be no overlapping in that case. For larger wave amplitudes, overlapping of resonances may take place; therefore the particle may satisfy two resonant conditions at the same time and its motion becomes random (stochastic), with its energy increased in the process.
In terms of the wave amplitude, for the high-frequency IA wave (ω > Ωi) the condition for stochastic heating reads 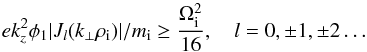 (35)Here, kz,k⊥ are the parallel and perpendicular wave-number components with respect to the magnetic field vector, φ1 is the wave potential, ρi,Ωi are the ion gyro-radius and gyro-frequency, Jl is the Bessel function, and l is any integer that describes higher harmonics. The heating acts mainly on the ions in the tail of the distribution function. Similarly, for the ion cyclotron (IC) and the lower-hybrid (LH) waves, the necessary threshold (Karney & Bears 1977; Karney 1978) can be written as E/B0 > (Ωi/ω)1/3(ω/k⊥)/4. These modes stochastically heat mainly the bulk plasma. The condition for the onset of the stochastic behavior in the case of the IA wave (35) is obtained simply from the condition that the sum of two half-width of adjacent resonances exceeds the separation between them (Smith & Kaufman 1975; 1978). The heating is typically very rapid, with the rates comparable to the gyro-frequency Ωi, and is also very efficient for the IA waves that propagate at an angle with respect to the magnetic field vector. Clearly, this implies that the wave frequency exceeds the gyro-frequency Ωi. Following Smith & Kaufman (1978), the optimal case is when the wave frequency is around 3–4 times the gyro-frequency. This is the reason why in Sect. 3.1 we restricted analysis to high-frequency IA waves; the instability obtained there will in fact remain for a rather wide range of wavelengths and frequencies. Also note that, as discussed in Smith & Kaufman (1978), this does not exclude the heating in the low frequency regime ω < Ωi, although it will not be as strong as in the previous case.
(35)Here, kz,k⊥ are the parallel and perpendicular wave-number components with respect to the magnetic field vector, φ1 is the wave potential, ρi,Ωi are the ion gyro-radius and gyro-frequency, Jl is the Bessel function, and l is any integer that describes higher harmonics. The heating acts mainly on the ions in the tail of the distribution function. Similarly, for the ion cyclotron (IC) and the lower-hybrid (LH) waves, the necessary threshold (Karney & Bears 1977; Karney 1978) can be written as E/B0 > (Ωi/ω)1/3(ω/k⊥)/4. These modes stochastically heat mainly the bulk plasma. The condition for the onset of the stochastic behavior in the case of the IA wave (35) is obtained simply from the condition that the sum of two half-width of adjacent resonances exceeds the separation between them (Smith & Kaufman 1975; 1978). The heating is typically very rapid, with the rates comparable to the gyro-frequency Ωi, and is also very efficient for the IA waves that propagate at an angle with respect to the magnetic field vector. Clearly, this implies that the wave frequency exceeds the gyro-frequency Ωi. Following Smith & Kaufman (1978), the optimal case is when the wave frequency is around 3–4 times the gyro-frequency. This is the reason why in Sect. 3.1 we restricted analysis to high-frequency IA waves; the instability obtained there will in fact remain for a rather wide range of wavelengths and frequencies. Also note that, as discussed in Smith & Kaufman (1978), this does not exclude the heating in the low frequency regime ω < Ωi, although it will not be as strong as in the previous case.
The heating implies that the wave loses its energy, and this should be compensated by some moderate instability that may keep the wave amplitude above the required level (35). The instability that appears in interpenetrating plasmas, presented in Sect. 3.1, may clearly serve this purpose. Following the prescription for the most effective heating given in Smith & Kaufman (1978), the model should be restricted to weakly collisional plasmas and to short perpendicular wavelengths. From Eq. (35) and for parameters assumed in Sect. 3.1, we have the critical amplitude of the wave potential of only φc = 0.41 V. This implies that the ratio eφc/(κT) = 0.005 is still a rather small quantity; thus the level of electrostatic fluctuations is rather low, yet strong enough to cause rapid and substantial heating as predicted by Smith & Kaufman (1978).
4. Summary
In this work a new kind of IA wave is derived, with rather different features as compared to ordinary IA waves in a homogeneous environment. The mode can spontaneously be excited, provided the simultaneous presence of the transverse electromagnetic wave and density gradient; it has a cut-off and can be backward. The excitation and coupling to the transverse wave is a purely linear effect. The cut-off is quantitatively and qualitatively very different from the IA wave cut-off that follows from the stratification of plasma in an external gravity field (Wahlberg & Revenchuk 2003; Vranjes 2011d), which also implies a plasma with inhomogeneous density. This new kind of IA wave in hot ion plasmas is in principle damped due to the Landau effect; however, it is shown that the damping is drastically reduced due to the presence of the cut-off, which pushes the resonance towards the tail of the distribution function, where the number of resonant ions is much smaller. These effects are presented quantitatively for the coronal plasma parameters. The dissipation still remains, and it in fact opens up a possibility for a direct transfer of radiation energy (from transverse electromagnetic light waves) to plasma internal energy and heating (by excitation of the IA wave and its consequent dissipation).
We stress that for the purpose of using Landau damping within the fluid theory, we have presented an excellent and very useful method suggested many years ago by D’Angelo et al. (1979), but completely overlooked by scientific community.
One new kind of instability of IA wave that develops in permeating plasmas, which was discovered in Vranjes et al. (2009), is also discussed in the application to the solar corona. It is shown that this instability can be rather effective (it has a much lower threshold than the instability in the usual electron-ion plasma with one component moving with respect to the other), it is currentless, and it can excite the IA wave even in environments with hot ions like the solar corona. We have discussed the high-frequency range of the IA waves, which consequently may propagate practically at any angle with respect to the background magnetic field. Such IA waves are known to cause stochastic heating, and this effect is discussed in application to the solar corona. This mechanism of stochastic heating is completely different than the dissipative heating due to the Landau damping mentioned above.
In the presence of collisions, the Landau damping can be reduced (Ono & Kulsrud 1975), but this may be expected only for wavelengths considerably exceeding the mean free path of particles. So in the case of the high-frequency IA waves discussed in Sect. 3, this is not expected to play any role. The same holds for the wavelengths used in Sect. 2; however, in principle for larger wavelengths the Landau dissipation may require longer time intervals.
Online material
Appendix A: Landau damping of ion acoustic waves in fluid theory
Appendix A.1: Elements of kinetic description
Within the two-component kinetic theory, Landau damping is well known. Here, we give a few details only in order to compare it with fluid description presented below in Sect. A.2. Small electrostatic perturbations of the form exp( − iωt + ikz) yield the dispersion equation ![\appendix \setcounter{section}{1} \begin{eqnarray} &&1+ \sum_{j} \frac{1}{k^2 \lambda_{\rm d}j^2} [1- Z(b_{j})]=0, \label{k6} \\[2mm] \nonumber &&b_{j}=\frac{\omega- k v_{j0}}{k \vtj}, \quad \lambda_{\rm d}j=\frac{\vtj}{\omega_{\rm p}j}, \quad \omega_{\rm p}j^2= \frac{q_j^2 n_{j0}}{\varepsilon_0 m_{j}}, \\[2mm] \nonumber &&Z(b_{j})=\frac{b_{j}}{(2 \pi)^{1/2}} \int_{\rm c} \frac{\exp(- \zeta^2/2)}{b_{j}- \zeta} {\rm d}\zeta. \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq181.png) (A.1)The dispersion Eq. (A.1) describes the plasma (Langmuir) and the IA oscillations, and ζ = vz/vTj.
(A.1)The dispersion Eq. (A.1) describes the plasma (Langmuir) and the IA oscillations, and ζ = vz/vTj.
For the present case with electrons and ions and in the limit 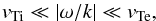 (A.2)the standard expansions may be used
(A.2)the standard expansions may be used 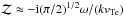 , and
, and ![\hbox{${\cal Z} \approx 1+ (k v_{{\rm Ti}}/\omega)^2 + 3 (k v_{{\rm Ti}}/\omega)^4 + 15 (k v_{{\rm Ti}}/\omega)^6 + \cdot\cdot\cdot - {\rm i} (\pi/2)^{1/2}[\omega/(k v_{{\rm Ti}})]\exp\{- [\omega/(k v_{{\rm Ti}})]^2/2\}$}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq185.png) , where ω = ωr + iγ is complex and its real part is assumed to be much larger than its imaginary part. The procedure yields the dispersion equation
, where ω = ωr + iγ is complex and its real part is assumed to be much larger than its imaginary part. The procedure yields the dispersion equation ![\appendix \setcounter{section}{1} \begin{eqnarray} &&1+ \frac{\omega_{\rm pe}^2}{k^2 v_{{\rm Te}}^2} \left[1+ {\rm i} (\pi/2)^{1/2} \frac{\omega}{k v_{{\rm Te}}} \right] - \frac{\omega_{\rm p i}^2}{k^2 v_{{\rm Ti}}^2} \Bigg\{ \frac{k^2 v_{{\rm Ti}}^2}{\omega^2} \nonumber \\[2mm] && + \frac{3 k^4 v_{{\rm Ti}}^4}{\omega^4} - {\rm i} (\pi/2)^{1/2} \frac{\omega}{k v_{{\rm Ti}}} \exp\left[-\omega^2/(2 k^2 v_{{\rm Ti}}^2)\right]\Bigg\} =0.\label{ap3} \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq187.png) (A.3)We introduce ℑ △ (ω,k) and ℜ △ (ω,k) denoting the imaginary and real parts of Eq. (A.3), respectively. Setting the real part ℜ △ (ω,k) = 0 yields the approximate expression for the IA spectrum
(A.3)We introduce ℑ △ (ω,k) and ℜ △ (ω,k) denoting the imaginary and real parts of Eq. (A.3), respectively. Setting the real part ℜ △ (ω,k) = 0 yields the approximate expression for the IA spectrum 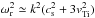 ,
, 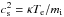 . The approximate Landau damping of the wave is obtained from
. The approximate Landau damping of the wave is obtained from ![\appendix \setcounter{section}{1} \begin{eqnarray} \gamma_{\rm app} &\simeq& - \Im \triangle(\omega, k)/[\partial \Re \triangle(\omega, k)/\partial \omega]_{\omega \simeq \omega_{\rm r}}\nonumber \\[2mm] &=&- k c_{\rm s} (\pi/8)^{1/2} \tau^{3/2} (1+ 3/\tau) \exp[-(\tau + 3)/2]. \label{ap4} \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq193.png) (A.4)Here, τ = Te/Ti, and we have assumed massless electrons and singly charged ions, that is, the Landau damping is due to the ions only. Otherwise, the electron contribution to the Landau damping
(A.4)Here, τ = Te/Ti, and we have assumed massless electrons and singly charged ions, that is, the Landau damping is due to the ions only. Otherwise, the electron contribution to the Landau damping 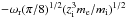 would appear in addition to the previously given Landau damping term, where zi is the ion charge number.
would appear in addition to the previously given Landau damping term, where zi is the ion charge number.
 |
Fig. A.1 Absolute value of the Landau damping of the IA wave (normalized to ωr) in terms of τ = Te/Ti. |
In Fig. A.1, we give the absolute value of the approximate (dotted line) Landau damping (8) (normalized to ωr) in terms of τ, together with the absolute value of the exact normalized Landau damping (full line) that may be obtained numerically from the general dispersion law (A.1). The nature of the dashed line will be given in Sect. A.2 below. It is seen that in the given range of τ the approximate kinetic expression (A.4) yields inaccurate values for the damping. For τ = 1, which is of interest for the solar corona, the exact Landau damping γex = 0.394ωr is larger by about a factor 2 than the approximate kinetic Landau damping γapp.
For practical purposes, we note that the exact kinetic Landau damping may conveniently be expressed in terms of τ by the following polynomial (cf. Chen 1984): ![\appendix \setcounter{section}{1} \begin{eqnarray} \nonumber &&|\gamma_{\rm ex}|/\omega_{\rm r} \simeq 0.681874541 -0.3697636428549\,\tau \\[2mm]\nonumber &&+0.09345888549671\,\tau^2 -0.01203427025053\,\tau^3 \\[2mm] &&+0.0007523967677\,\tau^4-0.000018\,\tau^5.\label{ex} \end{eqnarray}](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq202.png) (A.5)The difference between γex and γapp follows from the fact that, in the limit τ → 1, the assumptions used to obtain the approximate kinetic damping become violated. One is thus supposed to use the rather inconvenient general dispersion Eq. (A.1), which contains an integral. Below, we show that this problem may be circumvented by using the two-fluid theory and a modeled fluid-Landau damping.
(A.5)The difference between γex and γapp follows from the fact that, in the limit τ → 1, the assumptions used to obtain the approximate kinetic damping become violated. One is thus supposed to use the rather inconvenient general dispersion Eq. (A.1), which contains an integral. Below, we show that this problem may be circumvented by using the two-fluid theory and a modeled fluid-Landau damping.
Appendix A.2: Two-fluid description
We use the linearized momentum equation for the general species α in a quasi-neutral plasma 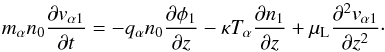 (A.6)The term with μL is the one introduced for the first time by D’Angelo et al. (1979) to describe the Landau damping effect on the fast solar wind streams with a spatially varying ratio τ( =Te/Ti) of the electron and ion temperatures. It is chosen in such a way to quantitatively describe the known properties of the Landau effect. These include the fact that the ratio d = δ/λ, between the attenuation length δ and the wavelength, is independent of the wavelength and the plasma density and dependent on τ in a prescribed way (Sessler & Pearson 1967; Andersen et al. 1968). These requirements appear to be fulfilled by
(A.6)The term with μL is the one introduced for the first time by D’Angelo et al. (1979) to describe the Landau damping effect on the fast solar wind streams with a spatially varying ratio τ( =Te/Ti) of the electron and ion temperatures. It is chosen in such a way to quantitatively describe the known properties of the Landau effect. These include the fact that the ratio d = δ/λ, between the attenuation length δ and the wavelength, is independent of the wavelength and the plasma density and dependent on τ in a prescribed way (Sessler & Pearson 1967; Andersen et al. 1968). These requirements appear to be fulfilled by 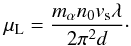 (A.7)Here,
(A.7)Here, 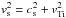 , while d(τ) satisfies a curve that is such that the attenuation is strong at τ ≈ 1 and weak for higher values of τ. It turns out that a sufficiently good choice for d(τ) is
, while d(τ) satisfies a curve that is such that the attenuation is strong at τ ≈ 1 and weak for higher values of τ. It turns out that a sufficiently good choice for d(τ) is
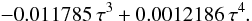 We observe that d(1) ≃ 0.4. We also use the ion continuity and in the massless electron limit from the electron momentum, we obtain just the Boltzmann distribution for electrons. This yields the dispersion equation for the Landau-damped IA wave
We observe that d(1) ≃ 0.4. We also use the ion continuity and in the massless electron limit from the electron momentum, we obtain just the Boltzmann distribution for electrons. This yields the dispersion equation for the Landau-damped IA wave 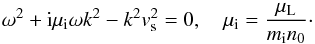 (A.8)For the complex frequency ω = ωr + iγf, we obtain
(A.8)For the complex frequency ω = ωr + iγf, we obtain 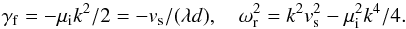 (A.9)
(A.9)
This shows that the mode oscillation frequency ωr is reduced as compared to the ideal plasma case, that is, without Landau damping. It is now appropriate to compare this fluid-modeled Landau damping γf with the exact kinetic damping given earlier. The normalized absolute fluid-modeled Landau damping | γf/ωr | ≃ 1/(2πd) is presented by the dashed line in Fig. A.1. The difference between γf and γex at τ = 1 is only 0.008. Clearly, the presented fluid-modeled Landau damping is, in fact, much more accurate than the approximate kinetic expression (A.4).
References
- Alexandrov, A. F., Bogdankevich, L. S., & Rukhadze, A. A. 1984, Principles of Plasma Electrodynamics (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Alfvén, H. 1947, MNRAS, 107, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Andersen, H. K., D’Angelo, N., Jensen, V. O., Michelsen, P., & Nielsen, P. 1968, Phys. Fluids, 11, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Bellan, P. M. 2006, Fundamentals of Plasma Physics (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Bello González, N., Franz, M., Martínez Pillet, V., et al. 2010, ApJ, 723, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Biermann, L. 1948, Z. Astrophys., 25, 161 [Google Scholar]
- Chen, F. F. 1984, Introduction to Plasma Physics and Controlled Fusion (New York: Plenum Press) [Google Scholar]
- D’Angelo, B. 1968, ApJ, 154, 401 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, N., Joyce, G., & Pesses, M. E. 1979, ApJ, 229, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Doveil, F. 1981, Phys. Rev. Lett., 46, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, J. Y., Matsuda, K., Chu, M. S., & Jensen, T. H. 1979, Phys. Rev. Lett., 43, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Karney, C. F. F. 1978, Phys. Fluids, 21, 1584 [NASA ADS] [CrossRef] [Google Scholar]
- Karney, C. F. F., & Bears, A. 1977, Phys. Rev. Lett., 39, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Kneer, F., & Bello González, N. 2011, A&A, 532, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ono, M., & Kulsrud, R. M. 1975, Phys. Fluids, 18, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzschild, M. 1948, ApJ, 107, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sessler, G. M., & Pearson, G. A. 1967, Phys. Rev., 162, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. R., & Kaufman, A. N. 1975, Phys. Rev. Lett., 34, 1613 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. R., & Kaufman, A. N. 1978, Phys. Fluids, 21, 2230 [NASA ADS] [CrossRef] [Google Scholar]
- Stix, T. H. 1992, Waves in Plasmas (New York: AIP) [Google Scholar]
- Vranjes, J. 2011a, A&A, 532, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vranjes, J. 2011b, MNRAS, 415, 1543 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J. 2011c, Phys. Plasmas, 18, 084501 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J. 2011d, Phys. Plasmas, 18, 062902 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J., & Poedts, S. 2006, A&A, 458, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vranjes, J., & Poedts, S. 2009a, Europhys. Lett., 86, 39001 [Google Scholar]
- Vranjes, J., & Poedts, S. 2009b, MNRAS, 400, 2147 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J., & Poedts, S. 2009c A&A, 503, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vranjes, J., & Poedts, S. 2010a, ApJ, 719, 1335 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J., & Poedts, S. 2010b, MNRAS, 408, 1835 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J., Saleem, H., & Poedts, S. 2007, Phys. Plasmas, 14, 034504 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J., Kono, M., Poedts, S., & Tanaka, M. Y. 2008, Phys. Plasmas, 15, 092107 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J., Poedts, S., & Ehsan, Z. 2009, Phys. Plasmas, 16, 074501 [NASA ADS] [CrossRef] [Google Scholar]
- Wahlberg, C., & Revenchuk, S. M. 2003, Phys. Plasmas, 10, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Weiland, J. 2000, Collective Modes in Inhomogeneous Plasmas (Bristol and Philadelphia: IOP Publishing) [Google Scholar]
All Figures
 |
Fig. 1 Mechanism of excitation of the longitudinal electrostatic field Elong ≡ Ez in the presence of a transverse wave with electric field in x direction, which propagates in z-direction. |
| In the text | |
 |
Fig. 2 Numerical solution of Eq. (16) for the IA wave in laboratory plasma with backward features and cut-off, both caused by interaction with transverse light wave in the presence of density gradient. |
| In the text | |
 |
Fig. 3 Numerical solution of Eq. (21) for IA wave in solar atmosphere. Line a: the usual IA wave in plasma with hot coronal ions. Line b: the IA wave propagating in the presence of the transverse light wave in plasma with density gradient. |
| In the text | |
 |
Fig. 4 Numerical solution of Eq. (23) for the IA wave spectrum. Dashed lines: the frequency (line a1) and absolute value of Landau damping (line a2) of the IA wave for homogeneous plasma with hot coronal ions. Full lines: the frequency (line b1) and damping (line b2) of the IA wave excited in the presence of the transverse light wave in inhomogeneous plasma. |
| In the text | |
 |
Fig. 5 Refraction and focusing of transverse electromagnetic wave with the wave number k in plasma with density gradient. |
| In the text | |
 |
Fig. 6 Growing IA wave in permeating coronal plasmas with the speed of the flowing quasi-neutral plasma with respect to the static plasma vf0 = 1.9cs. |
| In the text | |
 |
Fig. 7 Transition from damped to growing IA mode in permeating solar plasmas for λ = 2 m. |
| In the text | |
 |
Fig. A.1 Absolute value of the Landau damping of the IA wave (normalized to ωr) in terms of τ = Te/Ti. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



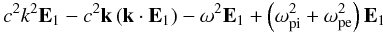
![$$ - \left\{\!\omega_{\rm pi}^2\vti^2 \left[\! \frac{1+ \delta_{\rm i2}}{\omega_{\rm i}^2} + \delta_{\rm i3} \left(\! 1+ \frac{k^2\vti^2}{\omega_{\rm i}^2} (1+ \delta_{\rm i2}) \!\right)\!\right] + \frac{\omega_{\rm pe}^2 \vte^2}{\omega_{\rm e}^2}\!\right\}\nabla \left(\nabla\!\cdot \! \vec E_1\right) $$](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq82.png)
![$$ \left[\omega^2 - \omega_{\rm pe}^2 - \omega_{\rm pi}^2 - k^2 \left(\frac{5 \omega_{\rm pi}^2 \vti^2/3}{\omega^2- 5 \omega_{\rm pi}^2 \vti^2/3} + \frac{\omega_{\rm pe}^2 \vte^2}{ \omega^2- k^2\vte^2}\right)\right] $$](/articles/aa/full_html/2013/06/aa21020-12/aa21020-12-eq86.png)