| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220631 | |
| Published online | 06 June 2013 | |
Online material
Appendix A: Bayesian model
Appendix A.1: Development of the model
To extract information about the EBL density from the data presented in Fig. 1, we develop a “hierarchical” Bayesian model (using the terminology of Gelman et al. 2003), which is described by source-by-source spectral parameters and global parameters specifying, among other things, the EBL density of primary interest here. We use a Bayesian methodology to write the posterior density for the model parameters, marginalize over the source-by-source parameters that are not of interest, and produce estimates and confidence intervals for the EBL density.
In the development below, we make repeated use of the conditional probability rule (CPR) that the joint probability of two (sets of) events A and B, P(A,B), can be expressed as P(A,B) = P(A | B)P(B). If the two events are independent this becomes P(A,B) = P(A)P(B). We also frequently use the rule for marginalizing (or integrating) over unwanted parameters, P(A) = ∫P(A,B)dB. Finally, we use the standard identity for the product of two Gaussians (see, e.g., Ahrendt 2005). In particular, if N(x | μ,σ2) denotes a Gaussian distribution with mean μ and variance σ2, then 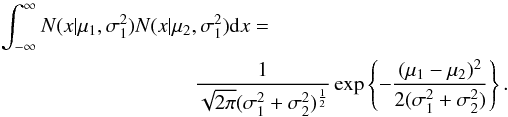 (A.1)The dataset to be modeled consists of N GeV and TeV spectral measurements,
(A.1)The dataset to be modeled consists of N GeV and TeV spectral measurements,  and
and 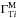 with measurement variances of
with measurement variances of  and
and 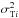 and redshifts zi (which are themselves not considered as measurement data). In what follows we refer frequently to the measured spectral break,
and redshifts zi (which are themselves not considered as measurement data). In what follows we refer frequently to the measured spectral break, 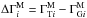 . We write the dataset as
. We write the dataset as  .
.
Each source is parametrized by four values, the intrinsic spectral indexes in the GeV and TeV regimes, 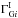 and
and 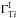 , and the spectral indexes after absorption by the EBL,
, and the spectral indexes after absorption by the EBL, 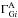 and
and 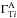 . In what follows we refer frequently to the intrinsic spectral break,
. In what follows we refer frequently to the intrinsic spectral break, 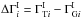 . The global parameters that describe the EBL absorption itself are denoted abstractly as G and we write the set of all parameters of the model as
. The global parameters that describe the EBL absorption itself are denoted abstractly as G and we write the set of all parameters of the model as 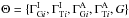 .
.
Bayes’ theorem allows us to write the posterior probability distribution of the parameters after the measurements have been made, P(Θ | Y), in terms of the standard likelihood of the data, P(Y | Θ), and the prior probability distribution of the model parameters, P(Θ):  The relation is written as a proportionality, instead of as an equality, because a global normalization factor has been neglected.
The relation is written as a proportionality, instead of as an equality, because a global normalization factor has been neglected.
The model has four primary components that we discuss below. These are: (1) the likelihood for the GeV and TeV measurements, given the true absorbed spectral indexes of the sources; (2) a relationship between the absorbed index in the GeV regime and the intrinsic (unabsorbed) index; (3) a relationship for the analogous indexes in the TeV regime; and (4) a specification of how the intrinsic index in the GeV regime is related to the intrinsic index in the TeV regime.
We assume that the measurements of the individual indexes are independent (no correlation between measurements from different sources or between the GeV and TeV bands) and that the distribution for each measurement ( or
or 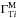 ) is Gaussian with mean given by the appropriate absorbed index and with variance given by the measurement errors squared. Therefore, the likelihood is
) is Gaussian with mean given by the appropriate absorbed index and with variance given by the measurement errors squared. Therefore, the likelihood is 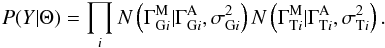 For the prior, we assume that the only link between the source-by-source index parameters for different sources comes through the global parameters G. Therefore, using the CPR we can write
For the prior, we assume that the only link between the source-by-source index parameters for different sources comes through the global parameters G. Therefore, using the CPR we can write 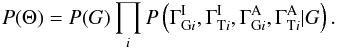 It now remains only to describe how the intrinsic and absorbed indexes for each source are related. We assume that the absorbed index in each band depends only on the intrinsic index in that band and on the EBL parameters. Repeatedly applying the CPR, this gives
It now remains only to describe how the intrinsic and absorbed indexes for each source are related. We assume that the absorbed index in each band depends only on the intrinsic index in that band and on the EBL parameters. Repeatedly applying the CPR, this gives 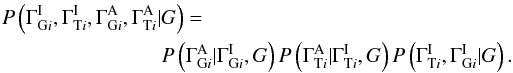 (A.2)We further assume that there is no absorption in the GeV regime and that the absorption in the TeV regime changes the index in a deterministic way. Specifically, we assume that (i)
(A.2)We further assume that there is no absorption in the GeV regime and that the absorption in the TeV regime changes the index in a deterministic way. Specifically, we assume that (i) 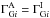 , and (ii)
, and (ii) 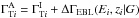 , where ΔΓEBL(Ei,zi | G) is a function giving the change in TeV index for a source at redshift zi measured at a TeV “threshold” energy of Ei. This can be expressed in terms of a probability using the Dirac δ-function:
, where ΔΓEBL(Ei,zi | G) is a function giving the change in TeV index for a source at redshift zi measured at a TeV “threshold” energy of Ei. This can be expressed in terms of a probability using the Dirac δ-function: 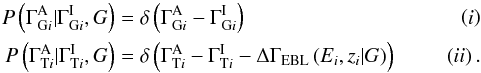 Equation (A.2) then reads
Equation (A.2) then reads 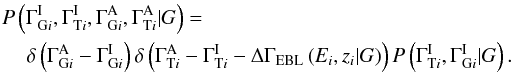 The final and most interesting part of the model is to describe how the intrinsic indexes in the two bands are related. We expand this using the CPR to give
The final and most interesting part of the model is to describe how the intrinsic indexes in the two bands are related. We expand this using the CPR to give 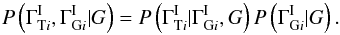 We adopt a uniform prior for
We adopt a uniform prior for 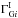 ,
, 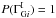 and restrict ourselves to forms for the conditional probability that can be expressed as a function of the intrinsic break,
and restrict ourselves to forms for the conditional probability that can be expressed as a function of the intrinsic break, 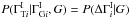 . We assume that the break for each source is drawn from a single universal distribution that has, at most, some dependence on the global parameter set, G. The final expression for the prior for the parameters of each source is
. We assume that the break for each source is drawn from a single universal distribution that has, at most, some dependence on the global parameter set, G. The final expression for the prior for the parameters of each source is 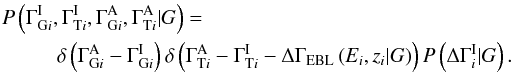 Putting everything together, recognizing that we have not yet discussed the parameters G, and leaving the exact choice of prior for the intrinsic break open for the present time, the full posterior density is
Putting everything together, recognizing that we have not yet discussed the parameters G, and leaving the exact choice of prior for the intrinsic break open for the present time, the full posterior density is 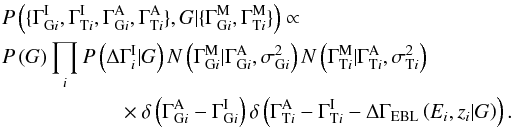 We marginalize over the parameters that are not of interest,
We marginalize over the parameters that are not of interest, 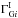 ,
, 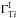 ,
, 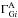 , and
, and 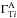 to give the posterior probability for the global parameters G. The integrals over the parameters for each source can be done separately:
to give the posterior probability for the global parameters G. The integrals over the parameters for each source can be done separately: 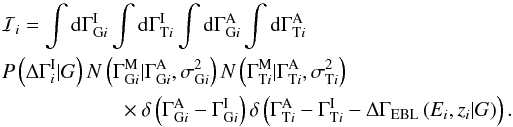 The integrals over
The integrals over 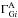 and
and 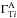 can be done immediately against the delta functions to give
can be done immediately against the delta functions to give 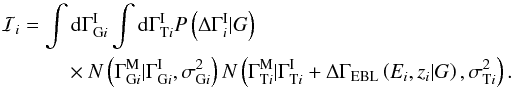 Making a change of integration variable from
Making a change of integration variable from 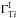 to
to 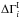 , the Gaussians can be manipulated to give
, the Gaussians can be manipulated to give 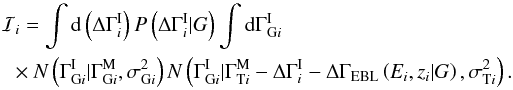 The second integral can be evaluated using Eq. (A.1). Putting all the source integrals together gives the general expression
The second integral can be evaluated using Eq. (A.1). Putting all the source integrals together gives the general expression 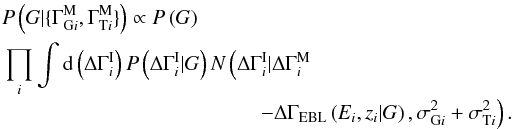 (A.3)
(A.3)
Appendix A.2: Various priors for 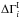
Summary of results from Bayesian model with different priors.
We examine three concrete cases for 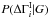 . The first two are based on simple assumptions and result in analytic expressions for the full posterior probability that are easy to understand. The final prior distribution is derived from Monte Carlo realizations of an SSC model, as described in Appendix B.1. The results from this final case are presented in Sect. 3.3. Here we develop the first two cases. A relatively weak assumption is that the TeV index can be no harder than the GeV index. It would seem reasonable to express this using the Heaviside step function, Θ(x), as
. The first two are based on simple assumptions and result in analytic expressions for the full posterior probability that are easy to understand. The final prior distribution is derived from Monte Carlo realizations of an SSC model, as described in Appendix B.1. The results from this final case are presented in Sect. 3.3. Here we develop the first two cases. A relatively weak assumption is that the TeV index can be no harder than the GeV index. It would seem reasonable to express this using the Heaviside step function, Θ(x), as 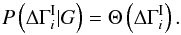 (A.4)However, this is unsatisfactory, as it asserts that the mean intrinsic break is infinite,
(A.4)However, this is unsatisfactory, as it asserts that the mean intrinsic break is infinite,  , which is clearly not realistic. As seen below, this results in an unphysical posterior distribution. To remedy this failing, we instead assume that the prior distribution of the intrinsic break is given by a Gaussian, truncated at negative values:
, which is clearly not realistic. As seen below, this results in an unphysical posterior distribution. To remedy this failing, we instead assume that the prior distribution of the intrinsic break is given by a Gaussian, truncated at negative values: 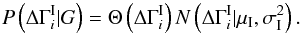 (A.5)In this case the prior is parametrized by two values, μI and σI, which must be either estimated in the problem (i.e., added to the global parameter set G) or specified externally. We will simply assume μI = 0 and derive the results for various reasonable values of σI.
(A.5)In this case the prior is parametrized by two values, μI and σI, which must be either estimated in the problem (i.e., added to the global parameter set G) or specified externally. We will simply assume μI = 0 and derive the results for various reasonable values of σI.
Equation (A.3) can be used to calculate the posterior distribution in the three cases for 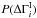 discussed above. In the second case, with the prior given by Eq. (A.5), the final integration can be done to give, after applying the formula for the product of Gaussians,
discussed above. In the second case, with the prior given by Eq. (A.5), the final integration can be done to give, after applying the formula for the product of Gaussians, 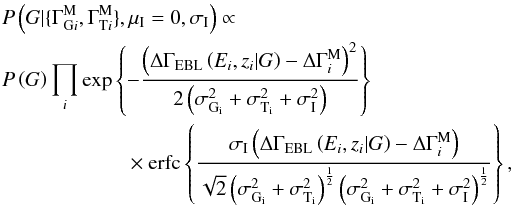 (A.6)where
(A.6)where 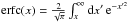 is the complementary error function.
is the complementary error function.
It is instructive to examine the two limiting cases of σI = 0 and σI → ∞. In the first case, we arrive at 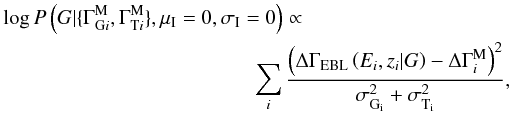 which is exactly the expression that would result from a simple least-squares fit to the measured spectral breaks. In the second case (σI → ∞), we have
which is exactly the expression that would result from a simple least-squares fit to the measured spectral breaks. In the second case (σI → ∞), we have 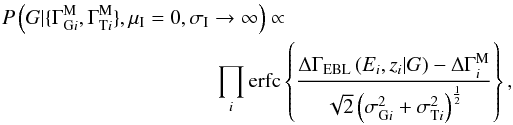 (A.7)which is the same expression as would be derived starting from the prior given by Eq. (A.4). We therefore have an expression that transforms continuously between the two clearly identifiable extremities as a function of σI.
(A.7)which is the same expression as would be derived starting from the prior given by Eq. (A.4). We therefore have an expression that transforms continuously between the two clearly identifiable extremities as a function of σI.
As described in Sect. 3.3, we attempt to derive constraints on two simple models for the EBL: (1) a linear approximation, given by Eq. (1), and (2) a scaling of the EBL model of Franceschini et al. (2008), as described by Eq. (2). In both cases, we assume a uniform prior in the positive region of the parameter space for a, P(a) = Θ(a) and α, P(α) = Θ(α), respectively.
Using either of these, the deficiencies in the model given by Eq. (A.4) is finally evident. Combining Eqs. (2) and (A.7), we get 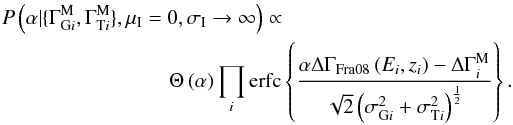 (A.8)The most probable value occurs at α = 0, which is consistent with the assertion in this case that
(A.8)The most probable value occurs at α = 0, which is consistent with the assertion in this case that 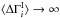 .
.
The results in Sect. 3.3 are derived from combining Eqs. (1) (or (2)) and (A.3) with the prior calculated in Appendix B.1 and integrating numerically.
Prediction of mean redshift value ⟨ z ⟩ and upper limit zP < 95% for a give value of ΔΓ.
Appendix A.3: Results with different priors
Table A.1 presents the results obtained with the half-Gaussian prior of Eq. (A.5) (with μI = 0) for four values for the variance of the distribution of the intrinsic break, σI = 0.25,0.5,1.0, and 2.0, and using the prior derived from SSC modeling, illustrated in Fig. B.1.
With increasing value of σI, the most probable value of a or α decreases, since a lower EBL-induced break is needed to reproduce the data. Results derived with values of σI = 0.5 and 1.0 are in good agreement with those from the SSC model.
Appendix A.4: Constraints on the redshift
The Bayesian methodology can also be used to constrain the redshifts of GeV-TeV blazars from their measured spectral breaks. In the case of a single source, Eqs. (A.3) and (2) can be adopted to express the posterior probability for the parameters G = { α,z }, given their priors P(α) and P(z)4. This can then be marginalized over α to give 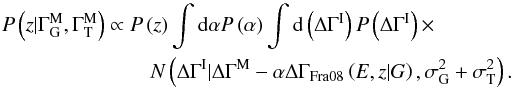 (A.9)The prior for the redshift, P(z), could be estimated from the redshift distribution of detected GeV-TeV detected blazars, i.e., from the values presented in Table 1. However, the true distribution is probably not well represented by the small number of sources detected, so we seek an alternative approach. Another option is to use a flat distribution, which is conservative but also unrealistic. We instead compromise and use the distribution of 2FGL BL Lac objects and unknown AGN. Since Fermi AGN are detected to higher redshifts than those at TeV energies, this should still be a conservative approach. For the prior on the EBL scaling, P(α), we use the positive portion of a Gaussian with mean 1.0 and RMS 0.3, P(α) = Θ(α)N(α | 1.0,0.32). Finally, we use the prior on ΔΓI derived from our SSC simulations, as described above.
(A.9)The prior for the redshift, P(z), could be estimated from the redshift distribution of detected GeV-TeV detected blazars, i.e., from the values presented in Table 1. However, the true distribution is probably not well represented by the small number of sources detected, so we seek an alternative approach. Another option is to use a flat distribution, which is conservative but also unrealistic. We instead compromise and use the distribution of 2FGL BL Lac objects and unknown AGN. Since Fermi AGN are detected to higher redshifts than those at TeV energies, this should still be a conservative approach. For the prior on the EBL scaling, P(α), we use the positive portion of a Gaussian with mean 1.0 and RMS 0.3, P(α) = Θ(α)N(α | 1.0,0.32). Finally, we use the prior on ΔΓI derived from our SSC simulations, as described above.
The mean redshift and upper limits for some values of ΔΓ, calculated using a typical value of 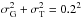 , are given in Table A.2. The corresponding relation between ⟨ z ⟩ and ΔΓ can be approximated by
, are given in Table A.2. The corresponding relation between ⟨ z ⟩ and ΔΓ can be approximated by  and the relation between zP < 95% and ΔΓ by
and the relation between zP < 95% and ΔΓ by 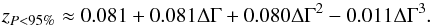
Appendix B: Synchrotron self-Compton simulations
Appendix B.1: Determination of the intrinsic break properties
 |
Fig. B.1
ΓVHE − ΓHE distribution (red histogram) obtained with the SSC simulations and application of cuts described in the text. |
| Open with DEXTER | |
 |
Fig. B.2
Value of ΔΓ as a function of the redshift z. The gray line is the break due to redshift effect as computed with the SSC simulation. |
| Open with DEXTER | |
In order to derive a plausible prior probability density for the intrinsic break between HE and VHE for use in the Bayesian model, we produce a set of Monte Carlo simulations of hypothetical BL Lacs using a one-zone SSC model (Band & Grindlay 1985), which is often used to successfully reproduce the time-averaged SEDs from radio to TeV energies.
Parameters used for the SSC simulations.
We assume a spherical emission zone, with a size R, moving at a bulk Doppler factor δ. This region is filled by a uniform magnetic field B, and a population of electrons with a density Ne(γ) is responsible for the synchrotron emission. The synchrotron photons are upscattered by the same population of electrons to produce γ rays.
The distribution of electrons is described by a power law with an exponential cutoff (Lefa et al. 2012), Ne(γ) = N0γp·exp( − γ/γcut). The model therefore has three parameters to describe the electron population (N0, p, and γcut) and four to describe the jet properties (z, R, δ, and B). Among these parameters, R, δ, and N0 have only an achromatic effect, and z produces a small K correction, which is evaluated separately in Appendix B.2. The spectral break is also insensitive to the value of the index p of the electron distribution. The parameters that determine the intrinsic break are therefore B and γcut.
We perform 105 simulations in which the values of B and γcut are uniformly drawn in the range 0.01 < B < 0.5 G and 3 × 104 < γcut < 1 × 107. The other parameters are kept fixed at the values given in Table B.1, which are typical for BL Lacs.
Since only the BL Lac-type SEDs are of interest in this study, simulations have been removed for which the synchrotron emission peaks at energies lower than 10 eV or higher that 10 MeV and which have an HE index of Γ > 2. The distribution of the intrinsic break 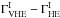 , depicted in Figure B.1, has a sharp rise below 0.2 and a long tail at higher break values.
, depicted in Figure B.1, has a sharp rise below 0.2 and a long tail at higher break values.
Appendix B.2: Effects of the energy shift due to the distance
The SSC simulations can be used to evaluate the size of the K correction required to account for the redshifting of the intrinsic spectrum into the fixed HE and VHE observation windows. This effect produces a trend of increasing observed ΔΓ with z, even in the absence of EBL absorption.
As before, the SSC parameters are fixed to the values in Table B.1, but with B = 0.1 G and γcut = 1.6 × 105. This produces an intrinsic spectrum with 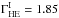 and
and 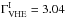 , i.e., ΔΓI = 1.19. Simulating the same source with redshifts in the range 10-4 < z < 0.7 and with no EBL absorption leads to an additional component in the observed ΔΓ, which increases with redshift, as depicted in Fig. B.2. This corresponds to the K correction for this intrinsic spectral shape and is too small to explain the trend observed in the data.
, i.e., ΔΓI = 1.19. Simulating the same source with redshifts in the range 10-4 < z < 0.7 and with no EBL absorption leads to an additional component in the observed ΔΓ, which increases with redshift, as depicted in Fig. B.2. This corresponds to the K correction for this intrinsic spectral shape and is too small to explain the trend observed in the data.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


