| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220916 | |
| Published online | 15 May 2013 | |
Online material
Appendix A: empirical correction for internal extinction
 |
Fig. A.1
Top: observed color (g − i)-stellar mass diagram of all 5026 optically selected galaxies from SDSS (subsamples 1+2) divided by morphological types: ETGs (dE-S0a, red), LTG (Sa-Im-BCD, blue). Many high-mass LTGs overlap with, or are even redder than, ETGs of similar mass. Bottom: same as above but (g − i)o is corrected for inclination as described in this appendix. The correction is visible at high mass where LTGs have now bluer colors than ETGs. The blue and red sequence become more parallel and a significant green valley opens up between them. |
| Open with DEXTER | |
 |
Fig. A.2
(Top panel) Observed color (g − i) – stellar mass diagram (subsamples 1+2) of edge-on LTGs (incl > 80, red) and of face-on LTGs (incl < 30, black), each with the linear best fit (dashed line). (Bottom panel) The slope of the fit to the color (g − i) – stellar Mass relation of disk galaxies (Sa-Sdm) (see Fig. A.2) as a function of galaxy inclination. |
| Open with DEXTER | |
An exhaustive treatment of the internal extinction correction to the u,g,r,i,z magnitudes is beyond the scope of this work and will be addressed in a forthcoming paper. We concentrate on a less ambitious task, i.e., on the empirical method for correcting the color magnitude relation for the effects of internal extinction. The color (g − i) versus stellar mass diagram (see Fig. A.1, color-coded according to the Hubble type) composed of all optically selected galaxies (regions 1 and 2) contains a well-developed red-sequence (e.g. Hogg et al. 2004) mostly composed of ETGs along with the so-called blue cloud, mostly composed of LTGs. When magnitudes are not corrected for internal extinction the two color sequences, that are well separated at low mass by the green valley, overlap one another at the high-mass end. This is an obvious consequence of the increasing internal extinction suffered by disk galaxies of increasing mass. Given the abundant number statistics offered by SDSS, it is possible to investigate this effect as a function of galaxy inclination in the plane of the sky. For disk galaxies (Sa through Sdm) the inclination incl with respect to the line of sight was computed following Solanes et al. (1996) assuming that spirals are oblate spheroids of intrinsic axial ratio q: 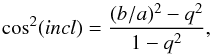 (A.1)where a and b are the major and minor axes. Intrinsic axial ratios were assumed to be equal to the modal values of the distribution of true ellipticities of galaxies of different Hubble types in the Second Reference Catalog of Bright Galaxies (de Vaucouleurs & Corwin 1976). For the giant spirals these are q = 0.32 for Sa, q = 0.23 for Sab, and q = 0.18 for Sb-Sc. Whenever b/a < q, incl is set to 90°. Irregulars+BCD (mostly low-mass objects) do not have this parameter defined, because their axial ratio does not give a measure of the inclination of the disk, but of their intrinsic triaxiality.
(A.1)where a and b are the major and minor axes. Intrinsic axial ratios were assumed to be equal to the modal values of the distribution of true ellipticities of galaxies of different Hubble types in the Second Reference Catalog of Bright Galaxies (de Vaucouleurs & Corwin 1976). For the giant spirals these are q = 0.32 for Sa, q = 0.23 for Sab, and q = 0.18 for Sb-Sc. Whenever b/a < q, incl is set to 90°. Irregulars+BCD (mostly low-mass objects) do not have this parameter defined, because their axial ratio does not give a measure of the inclination of the disk, but of their intrinsic triaxiality.
Figure A.2 (top panel) shows the g − i color versus stellar mass diagram for LTGs in regions 1+2 considering only nearly edge-on (incl > 80) and nearly face-on (incl < 30) galaxies, with the best linear fit. It is evident that the fits cross each other near log M∗ = 8.0, i.e., the extinction correction is null near log M∗ = 8.0, and it increases with increasing stellar mass as a function of the inclination. The slope of the relation as a function of the cosine of the inclination is given in Fig. A.2 (bottom panel). This relation can be used to extrapolate g − i to the face-on value, or to obtain the color correction for internal extinction: 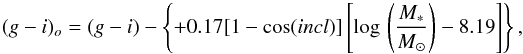 (A.2)where incl is the galaxy inclination. After applying the empirical internal extinction correction the resulting slope of the LTG sequence becomes similar to the one of ETGs, and the green-valley opens up over the full interval of masses (Fig. A.1 bottom panel). Note the difference between the correction method proposed here (which depends on a combination of M∗ and incl) and the one proposed by Yip et al. (2011), which purely depends on incl.
(A.2)where incl is the galaxy inclination. After applying the empirical internal extinction correction the resulting slope of the LTG sequence becomes similar to the one of ETGs, and the green-valley opens up over the full interval of masses (Fig. A.1 bottom panel). Note the difference between the correction method proposed here (which depends on a combination of M∗ and incl) and the one proposed by Yip et al. (2011), which purely depends on incl.
Appendix B: Scaling relations
Hα3, which is based on an ALFALFA-selected sample in the Coma supercluster provides us with insufficient coverage of HI mass, stellar mass, and SFR because of the shallowness of ALFALFA at the distance of Coma. Therefore the analysis of the scaling relation among the HI gas content and the stellar mass of galaxies cannot be undertaken with a sufficient dynamical range of HI mass, stellar mass, and SFR. However by adding the results of the present survey with similar ones obtained in Paper II for the Local Supercluster (where the ALFALFA sensitivity is 35 times better), we broaden the dynamic range to four decades in stellar mass, obtaining the relations shown in Fig. B.1, whose linear regression parameters are listed in Table B.1. The data obtained in this paper for the Coma supercluster for galaxies with DefHI ≤ 0.2 are plotted separately (blue symbols) from those in the Local Supercluster with DefHI ≤ 0.3 taken from Paper II (light gray). AGNs of various levels of activity are identified in Fig. B.1 (with asterisks) according to the criteria of Gavazzi et al. (2011).
We begin by studying the relation between MHI and M∗, as shown in Fig. B.1a. The diagonal lines represent the sensitivity limit of ALFALFA, computed for galaxies with an inclination of 45 deg (see Sect. 2.2). The dotted line is computed for the distance of the Virgo cluster (17 Mpc), while the dashed one is for the distance of Coma (100 Mpc). Clearly the observed distribution for Coma lies very close to the line of limiting sensitivity, making the observed slope (0.34) spuriously shallow because galaxies near log (M∗/M⊙) ~ 8 and log (MHI/M⊙) ~ 8, which are present locally, would not be detected at the distance of Coma. However, at the high-mass end of the stellar mass function, where the sampling is more abundant in Coma than locally because of the larger volume, no selection effects would prevent us from detecting galaxies if they had the same steep slope as extrapolated from the Local Supercluster. Therefore we conclude that the change of slope seen in Fig. B.1a near log (M∗/M⊙) ~ 9 is real. A relation similar to the one in Fig. B.1a and b, i.e.,
significant flattening above log (M∗/M⊙) ~ 8, has been obtained by Huang et al. (2012) using the whole α.40 sample. They interpreted the flattening as a possible evidence of increasing gas loss due to AGN feedback with increasing mass.
We note that the observed relation, both in the steep part (0.47) and in the shallow (0.32), is nonetheless significantly shallower than the direct proportionality, as already discussed in Gavazzi et al. (2008) and in Paper II, reflecting a genuine non-proportionality between the two quantities. When the HI gas fraction MHI/M∗ is plotted as a function of the stellar mass (Fig. B.1b), the fraction of gas decreases by approximately 2 orders of magnitude with increasing galaxy mass, from log (M∗/M⊙) ~ 7.5 to ~11.5. In other words, 107.5 M⊙ galaxies contain ten times more gas than stars. This ratio is reduced to less than 10% in 1011.5 M⊙ systems. This basic result agrees perfectly with what was found in the (optically selected) GASS survey by Catinella et al. (2010) in the stellar mass range 1010 < M∗ < 1011.5 M⊙ and by Cortese et al. (2011) for HI-normal galaxies in the Herschel Reference Survey (HRS; Boselli et al. 2010). It is also consistent with the downsizing scenario (Gavazzi 1993; Gavazzi et al. 1996; Cowie et al. 1996; Gavazzi & Scodeggio 1996; Boselli et al. 2001; Fontanot et al. 2009), where progressively more massive galaxies have less gas-to-star ratio at z = 0 because they have transformed most of their gas into stars at higher z, while dwarf LTGs retain large quantities of hydrogen capable of sustaining the star formation at some significant rate at the present cosmological epoch.
Similarly, we find that the relation between the SFR and the stellar mass (Fig. B.1c) and that of the specific SFR with stellar mass (d) are consistent with a change of slope around log (M∗/M⊙) ~ 9. Below that threshold a steeper dependence (0.8, i.e., almost of direct proportionality) is traced by the local galaxies. Above this limit the relation is much shallower (0.33) and is followed by the more distant Coma galaxies. Consequently, in the range of stellar mass covered by the Coma supercluster the specific star formation rate decreases significantly with increasing mass, as found by Boselli et al. (2001), Bothwell et al. (2009) and by Schiminovich et al. (2010). This is again consistent with the “downsizing” scenario. At lower mass the relation flattens out and the scatter increases by 2 orders of magnitude, as noted by other authors (Lee at al. 2007; Bothwell et al. 2009). The curvature in Fig. B.1 resulting from the superposition of the local and Coma superclusters is consistent with the change of slope found by Huang et al. (2012) in α.40.
 |
Fig. B.1
Principal scaling relations between MHI, M∗, and SFR in the Coma supercluster covered by ALFALFA. Blue: DefHI ≤ 0.2; red: DefHI ≥ 0.2 compared to the DefHI ≤ 0.3 in the Local Supercluster (grey, Paper II). Symbols are assigned according to the morphology: spirals (Sa-Sdm): squares; Irr-BCD: triangles; AGN: asterisks. Top-left panel: the MHI versus M∗ relation The diagonal lines represent the limiting sensitivity of ALFALFA (computed for a mean incl = 45°) at the distance of Virgo (gray dotted) and of Coma (black dashed). The shallow sensitivity of ALFALFA limits significantly the detection of galaxies at the distance of Coma, in particular with decreasing stellar mass. Top-right panel: the HI gas fraction (MHI/M∗) versus M∗. Bottom-left panel: the relation between the SFR and the stellar mass. Bottom-right panel: the specific star formation rate versus stellar mass. |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


