| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | L7 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201220771 | |
| Published online | 19 February 2013 | |
Online material
Appendix A: Iterative maximization approach
We assume that the optimal model point position is shifted by some small distance,
δφi,
relative to the grid point location found using RMCLEAN,
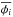
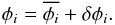 (A.1)The ML solution is
obtained by minimizing H in Eq. (4) with respect to
δφi, which gives
(A.1)The ML solution is
obtained by minimizing H in Eq. (4) with respect to
δφi, which gives
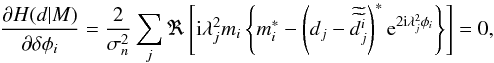 (A.2)where
(A.2)where
 is the same as
is the same as 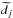 ,
Eq. (2), except that the sum is over
k ≠ i. The operator ℜ selects the real part of its
argument. This expression cannot be solved analytically for
δφi, but we can use it
to search for the solutions iteratively. To do so we Taylor expand the exponential term
in Eq. (A.2) to first order, thereby
making H second order in
δφi. This gives
,
Eq. (2), except that the sum is over
k ≠ i. The operator ℜ selects the real part of its
argument. This expression cannot be solved analytically for
δφi, but we can use it
to search for the solutions iteratively. To do so we Taylor expand the exponential term
in Eq. (A.2) to first order, thereby
making H second order in
δφi. This gives
 (A.3)which we can rewrite in
the form
(A.3)which we can rewrite in
the form 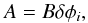 (A.4)where
(A.4)where
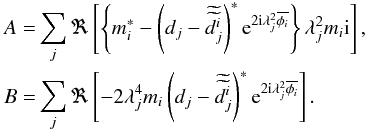 (A.5)We
must also solve for an updated flux. We can again extremize Eq. (4), this time with respect to
mi. We find
(A.5)We
must also solve for an updated flux. We can again extremize Eq. (4), this time with respect to
mi. We find
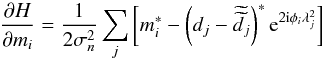 (A.6)and
thus
(A.6)and
thus
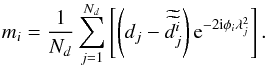 (A.7)In our example
implementation, we solve for δφ and m iteratively
until convergence is achieved. We also attempt to merge nearby model components to
reduce the degrees of freedom in the model according to the prescription described in
Sect. 2.
(A.7)In our example
implementation, we solve for δφ and m iteratively
until convergence is achieved. We also attempt to merge nearby model components to
reduce the degrees of freedom in the model according to the prescription described in
Sect. 2.
We tried other iterative schemes, e.g. solving for position and flux changes by inverting the Hessian matrix of H, but found that the approach given here is the most stable.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


