| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220454 | |
| Published online | 06 March 2013 | |
Online material
Appendix A: Interferometric observations
 |
Fig. A.1
Square visibilities (left), closure phases (middle) and corresponding reduced χ2 map (right) for the PIONIER observation of 2012-02-24. The corresponding best-fit binary model is shown in red. |
| Open with DEXTER | |
 |
Fig. A.2
Same as Fig. A.1 for the PIONIER observation of 2012-03-02. |
| Open with DEXTER | |
 |
Fig. A.3
Same as Fig. A.1 for the PIONIER observation of 2012-03-03. |
| Open with DEXTER | |
 |
Fig. A.4
Same as Fig. A.1 for the PIONIER observation of 2012-03-05. |
| Open with DEXTER | |
Appendix B: Computation of characteristic times for circularization and synchronization
Appendix B.1: Equilibrium tide
Press et al. (1975) provide explicit formulas. For each component of the binary, we have  Here N is the angular rotation velocity of the star, g is its gyration radius (the moment of inertia is defined as g2mR2), RT is an effective Reynolds number that can be taken ~20, and K and δ are numerical parameters. According to Press et al. (1975), we can typically assume K = 0.025 and δ = 0.1. The other symbols have their meaning introduced above. These formulas are valid for either component of the binary. In each case, m1 stands for the mass of the star we are considering, and m2 for the mass of the other star.
Here N is the angular rotation velocity of the star, g is its gyration radius (the moment of inertia is defined as g2mR2), RT is an effective Reynolds number that can be taken ~20, and K and δ are numerical parameters. According to Press et al. (1975), we can typically assume K = 0.025 and δ = 0.1. The other symbols have their meaning introduced above. These formulas are valid for either component of the binary. In each case, m1 stands for the mass of the star we are considering, and m2 for the mass of the other star.
Appendix B.2: Dynamical tides
Zahn (1977) gave characteristic times. 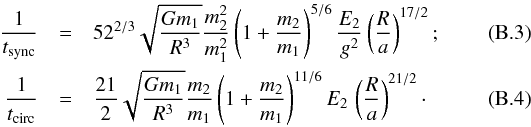
The conventions are the same as above. E2 is a dimensionless constant characteristizing the strength of the dynamical tide. Zahn (1975) provided a table of E2 and gyration radius at ZAMS for various masses. We interpolated these values for the actual masses and computed the characteristic times, assuming n = N and e = 0.
Appendix B.3: Tidally driven meridional currents
According to Tassoul & Tassoul (1992), the characteristic times in years are  (B.5)and
(B.5)and 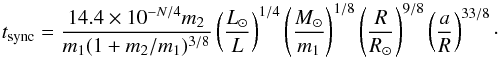 (B.6)L is the stellar luminosity and N is a charateristic exponent that can be taken as 10 for stars with a convective envelope, and 0 for stars with a radiative envelope, which is the case here.
(B.6)L is the stellar luminosity and N is a charateristic exponent that can be taken as 10 for stars with a convective envelope, and 0 for stars with a radiative envelope, which is the case here.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


