| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 22 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201219621 | |
| Published online | 04 February 2013 | |
Online material
Appendix A: Normalisation
In this section, we describe the semi-automatic procedure used to normalise the spectra discussed in this paper. The adopted algorithm uses all continuum points after automatically rejecting stellar and interstellar lines (both in emission and absorption) and cosmetic defects (bad columns, cosmic rays).
The global trend in the spectrum is first removed using a one-degree polynomial fitted to the continuum, resulting in a spectrum scaled around unity. A polynomial of degree 4 to 8 is then fitted to the scaled continuum. The error bars on the flux in each pixel are in principle provided by the ESO pipeline. By a comparison of the error spectra with the empirical S/N in continuum regions, we find that the pipeline actually overestimates the error spectra by a factor 1.2, which we correct for before using the pipeline-provided errors to weight the fit. The normalisation procedure proceeds as follows:
-
i.
the spectrum is smoothed using a 21-pixel wide median filter;
-
ii.
the spectral lines are removed by comparing the results of median and max/min filters applied on the initial spectrum, accounting for the spectrum S/N;
-
iii.
a first guess-solution of the continuum position is obtained using the smoothed spectrum (ii);
-
iv.
a second-guess solution is obtained using the smoothed spectrum (ii) after σ-clipping around (iii);
-
v.
the final solution is obtained using the original spectrum (i.e., no smoothing) after σ-clipping around (iv). Manual exclusion of specific regions is allow at this stage to incorporate a priori knowledge on unsuitable continuum regions (e.g., broad diffuse interstellar bands, broad emission regions);
-
vi.
the spectrum (v) is scaled by the median value computed over its continuum regions. This allows to correct for slight global under/over estimates of the average continuum level which occurs when there are many absorption/emission lines as the line wings may induce a small but systematic bias. This empirical correction is of the order of a fraction of a per cent;
-
vii.
the normalisation function is applied to the error spectrum.
Appendix B: Radial velocity measurements
Appendix B.1: Methodology
The choice of the RV measurement method is guided by the need to provide consistent, unbiased and homogeneous absolute RVs with representative error bars over the full range of O spectral sub-types and given the specificity of the data set. In our case, only a few lines are suitable for RV measurements. The number of epochs, the number of lines and their quality change from one star to another as a function of the star’s spectral type and brightness and the degree of nebular contamination. The S/N also varies significantly from one star to another, from one epoch to another and over different spectral regions.
Three RV techniques were considered: line moments, cross-correlation and Gaussian fitting. Tests were performed both on synthetic data and on a small set of objects taken from our survey. Synthetic spectra for a range of temperatures, gravities, projected rotational velocities (vsini) and S/N representative of the VFTS O star data were generated using fastwind (Puls et al. 2005) and degraded to the resolution of our survey. We briefly discuss the pros and cons of the three approaches below.
Line moments turn out to be very sensitive to residuals of the nebular correction and the accuracy of the method is not explored further. Auto cross-correlation (Dunstall et al., in prep.) provides accurate RVs and is rather robust against residuals of the nebular correction. However, for stars with less than four lines suitable for RV measurement, cross-correlation has intrinsic difficulties in providing accurate error bars. Gaussian fitting provides slightly less accurate RVs than cross-correlation, but with more reliable error bars for stars with only few lines of sufficient quality. However, the performance of Gaussian fitting degrades strongly with the quality of the lines (i.e., low S/N or high vsini).
To improve the performance of the Gaussian fitting, we developed a tool to allow us to fit all the available lines at all epochs (and both wavelength set-ups) simultaneously. We assume that the line profiles are constant and well described by Gaussians. Each considered line is required to have the same full-width at half-maximum (FWHMs) and amplitude (A) at all epochs. All the lines of a given epoch are further required to display the same RV shift. If L is the number of considered lines and N the number of epochs, the number of parameters in the fit is thus : N + 2 × L. Typical values for N are 18 and 6, depending on whether consecutive exposures are taken individually or summed up. Values for L vary between 2 and 5. This yields a maximum number of parameters of the order of 28 in the present approach, to be compared with the 3 × N × L = 270 parameters of the standard approach that adjusts each line separately. In essence the proposed method allows the line profile parameters (FWHMs and amplitudes) to be bootstrapped by the best quality spectra, improving the RV measurements of the lowest S/N data.
For simplicity and robustness in the SB2 cases (see below), we have chosen to fit the full line profile using Gaussians. Intrinsic He profiles are however not always well represented by Gaussian shapes. For slow rotators (vrotsini ≤ 80 km s-1), the shape of the line is dominated by the instrumental profiles that is well approximated by a Gaussian. The profile of moderately rotating stars (vrotsini ≤ 300 km s-1) is also well matched by a Gaussian, but with a small difference in the line wings. For fast rotators, rotationally broadened line profiles deviate significantly from the Gaussian shape. However, because we only attempt to measure the position of the centre of the lines and because the fitted lines are symmetric to within first-order, no significant bias is expected from this approximation.
The fitting method is based on least-square estimates where the merit function accounts for the error spectrum to provide individual error bars for each pixel. The optimisation relies on a modified Levensberq-Marquardt algorithm that requires a first estimate of the parameters. For constant RV stars and single-lined (SB1) binaries, the method is found to be robust against the initial guesses and we have taken v = 270 km s-1, FWHM = 3.0 Å and A = 0.1 to initialize the fit. The allowed ranges for the various parameters are as follow: v ∈ [−300, + 700] km s-1, A ∈ [0.0,0.6] and FWHM ∈ [0,10] Å. Only absorption lines were considered. For the doubled-lined spectroscopic binaries (SB2) in our sample, we follow the same approach with two Gaussian components per line profile. For some of the objects the initial guesses needed to be iterated once or twice to improve the quality of the SB2 fit.
Appendix B.2: Line selection
In this section, we discuss the choice of spectral lines suitable for relative and absolute RV measurements. The spectra of O-type stars are dominated by H i, He i and He ii lines. Hydrogen lines are generally poorer RV indicators than (most of) the He lines because they are broader and more sensitive to wind effects. The hydrogen lines of most of the VFTS O stars are also strongly affected by nebular emission. Metal lines (C, N, O, Si, Mg) are also present in O star spectra but are typically weaker than He lines. The presence of a given metal line is often limited to a small range of spectral sub-types and does not allow for an homogeneous approach across the O star domain. Our analysis is thus focused on the strong He i and He ii lines from 4000 to 5000 Å, i.e. He iλλ4387, 4471, 4713, 4922, He iiλλ4200, 4541, 4686 and the He i+ii blend at λ4026. In the rest of this section, we discuss the respective merits of each of these lines. Two aspects are important to consider:
-
the internal consistency, i.e. RV measurements from various lines of a given star should, coherently, reflect the systemic velocity of the star;
-
the homogeneity with respect to the full sample, i.e. the selected set of lines should provide RV measurements that can be compared to RVs from other stars even if only a sub-sample of the lines are available. This is important as the spectrum of early O stars is dominated by He ii lines and those of late O stars by He i lines.
Of all helium lines, stellar winds mostly affect He iiλ4686, though not all spectral sub-types or luminosity class are equally affected by the filling in of the photospheric absorption line by wind emission. We find that RVs obtained from He iiλ4686 are reliable for late and mid main-sequence sub-types. They are biased towards negative values by up to 25 km s-1 in early main-sequence stars. RVs from giants and supergiants are blue-shifted even for late-O stars and the line cannot be used as a probe for absolute RVs.
We also compare RV measurements obtained individually from different lines in a representative sub-sample of the O stars, covering the complete O spectral sub-range. Only stars displaying constant RVs are considered for this test. Because the line is observed both in the LR02 and LR03 setups and remains of a reasonable strength even in the latest O sub-types, we use the He iiλ4541 line as a reference for the comparison. Figure B.1 shows the difference between RVs obtained for a given line and those obtained from He iiλ4541 plotted against the spectral sub-type. Temperature effects on He i+iiλ4026 are clearly illustrated. Wind effects turn out to have a limited impact on He iiλ4686 measurements mostly because our sample is dominated by main-sequence stars and because many single supergiants present low-amplitude RV variations and are thus excluded from the comparison.
RVs from the He iλ4471 line show large discrepancies, which we attribute to the combination of the following factors: He iλ4471 is a triplet transition, with a forbidden component. It is quasi-metastable, similar to but less extreme than He iλλ3889, 5876, 10830 and is highly susceptible to wind effects. For late spectral sub-types it is blended with O ii in its blue wing and, among the measured He i lines, it suffers the most from the nebular contamination.
For late spectral types, He iiλ4200 is blended with N iiiλ4200.07 (i.e., about 17 km/s redwards from He iλ4200), which can explain some of the deviations seen in the corresponding panel in Fig. B.1. For late O stars, the uncertainties associated with He iiλ4200 RVs are large anyway and the line has a very limited weight in the final RV measurements obtained from simultaneously fitting all available lines (Fig. B.2).
 |
Fig. B.1
Difference between the RVs measured from individual He lines and those measured from He iiλ4541 as a function of the spectral sub-type. The panel at the bottom right corner compares RVs obtained using all available He lines (except He i+iiλ4026 and He iiλ4686) with the He iiλ4541 RVs. The dashed line indicates the average of all comparisons weighted by their uncertainties. Only stars with constant RVs and data points with σΔRV < 20 km s-1 have been included. |
| Open with DEXTER | |
 |
Fig. B.2
Comparison of the RVs measured using simultaneously all suitable He i and He ii lines (left and right panel, respectively) with the RVs measured using all suitable He lines. The He i+iiλ4026 and He iiλ4686 lines have not been used in the measurements. |
| Open with DEXTER | |
The best consistency is observed between the lines He iiλλ4200, 4541, He iλλ4387 and 4713. He iλ4922 displays good consistency over the range of O spectral sub-types but provides RVs that are on average shifted by 3 km s-1 compared to the other lines. We mitigate this by modifying the effective rest wavelength of the transition.
As a conclusion, up to five lines can be used for absolute RV measurements (He iiλ4200, 4541, He iλλ4387, 4713, 4922) depending on the spectral types, S/N and nebular contamination. He i+iiλ4026, and, for relatively weak wind stars, He iiλ4686 can be used for relative measurements.
Rest wavelengths (λ0) used to computed the RVs.
Appendix C: A Monte-Carlo method to constrain the intrinsic orbital parameter distributions
 |
Fig. C.1
Comparison between the observed (crosses) and simulated (lines) cumulative distributions of the peak-to-peak RV amplitudes (top row), variability time scales (middle row) and χ2 (bottom row). Lefthand panels vary the exponent π of the period distribution. Panels in the central column vary κ, the exponent of the mass-ratio distribution and the righthand panels vary η, the exponent of the eccentricity distribution. π, κ and η values are indicated in the upper-left legend of each panel. The bottom-right legends indicate the overall VFTS detection probability for the adopted parent distributions. |
| Open with DEXTER | |
In this section, we provide the details of the Monte-Carlo method used to constrain the intrinsic orbital parameter distributions. The general philosophy resembles that of Kobulnicky & Fryer (2007), in the sense that it relies on a Monte-Carlo modeling of the orbital velocities. On the one hand, we follow Kobulnicky & Fryer in using KS tests to compare simulated and observed distributions and the diagnostic distributions based on ΔRV and χ2 (see Sect. C.3) are similar to, respectively, the Vh and Vrms used by Kobulnicky & Fryer. On the other hand, our method fundamentally differs in various aspects. First we use the specific measurement errors provided by the RV analysis throughout the complete Monte-Carlo analysis. Second, we do not apply external constraints such as fixing the period distribution or using the fraction of Type Ib/c supernovae corresponding to each model. We thus attempt to simultaneously constrain the intrinsic period and mass-ratio distributions and the intrinsic binary fraction.
The core of the method is identical to that described in Sana et al. (2012) but differs in the adopted merit function. Sana et al. compared the observed orbital parameter distributions while we will use distributions constructed from the RV database. Indeed most of the detected binaries in 30 Dor have too few RV measurements to compute a meaningful orbital solution, precluding the direct approach used by Sana et al. (2012).
Appendix C.1: Method overview
As discussed in the main text, we use power laws to describe the intrinsic distributions of orbital parameters: f(log 10P/d) ~ (log 10P/d)π , f(q) ~ qκ and f(e) ~ qη, the exponents of which are left as free parameters. For each combination of π, κ and fbin in our grid, we draw populations of N = 360 primary stars using a Kroupa mass function (Kroupa 2001) between 15 and 80 M⊙, covering thus the expected mass range of O-type stars. Each star is assigned an observational sequence (observing epochs and RV accuracy at each epoch) from our VFTS sample. A fraction of these stars are randomly assigned to be binaries following a binomial with a success probability fbin. The orbital parameters of the binaries are randomly drawn as follows:
-
the period and mass-ratio are taken from the power-law distributions given π and κ;
-
–
the eccentricity is taken from a power-law distribution with an index given by η = −0.5 (see discussion in Sect. 4.1);
-
the inclination and periastron argument are taken assuming random orientation of the orbit in space;
-
the time of periastron passage is assumed to be uncorrelated with the observational sampling and is thus taken from a uniform distribution.
The binary detection criteria of Eq. (4) are then applied and the simulated detected binaries are
flagged. Simulated observed distributions (see Sect. C.3) are built based on the simulated RV
measurements of the detected systems and the simulated measured
binary fraction 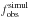 is
computed.
is
computed.
For a given combination of π, κ and
fbin the process is repeated 100 times to build the
parent statistics. The simulated parent distributions are then compared to the
observed ones by means of a one-sided KS test. We also compute the binomial
probability 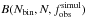 to
detect Nbin binaries among a population of
N stars given the success probability predicted by the simulations,
i.e.
to
detect Nbin binaries among a population of
N stars given the success probability predicted by the simulations,
i.e. 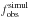 . Adopting
Nbin to be the actual number of detected O-type binaries
in VFTS allows us to estimate the ability of the assumed intrinsic parameters to
reproduce the observed binary fraction while taking into account the finite size of
the sample.
. Adopting
Nbin to be the actual number of detected O-type binaries
in VFTS allows us to estimate the ability of the assumed intrinsic parameters to
reproduce the observed binary fraction while taking into account the finite size of
the sample.
Appendix C.2: Diagnostic distributions
In this section, we specifically discuss the empirical distributions used as diagnostics. The choice of the merit function will be discussed in the next section. We investigate four diagnostic quantities:
-
i.
the distribution of, for each detected binary, the amplitude of the RV signal (ΔRV);
-
ii.
the distribution of, for each detected binary, the χ2 of a constant RV model;
-
iii.
the distribution of, for each detected binary, the minimum time scale for significant RV variations to be seen (ΔHJD);
-
iv.
the detected binary fraction.
Appendix C.3: Suitable merit functions
At each point of the grid defined by the the intrinsic values π, κ and fbin, the simulated distributions (i) to (iii) are individually compared to the observed ones using KS-tests while the simulated and observed binary fraction are compared using a binomial statistics. Because we aim at matching all the diagnostic distributions simultaneously, we also combine the individual probabilities in a global merit function.
We run several test to assess different merit functions (i.e., different ways of combining the individual probabilities) as well as to validate our method. We generate synthetic data from known input distributions, i.e. known π, κ and fbin, and we apply our code using different merit functions. Input and output distributions are then compared to check the suitability of the various merit functions as well as the general accuracy of the method. The process has been repeated using 50 synthetic data sets in each case. The synthetic data have been generated such that they share the same observational properties (sampling, measurement accuracy) as the VFTS Medusa data. Table C.1 provides an overview of the results of the tests. Because of the computational load of such tests, we use a slightly coarser grid with steps of 0.02 in fbin. Explored ranges in fbin, π and κ and steps in the power law indexes π and κ are identical to those quoted in Table 5. In addition to appraising the merit function, we also test the need to apply a minimal threshold C for the detected significant RV signal.
Overview of the test results using different merit functions (Col. 2).
The first striking result is that most merit functions can recover the input binary fraction within a few percents albeit with various precision. Some of the best results are obtained when including the B(Nobs,N,fsim) term in the merit function.
The index π of the period distribution is poorly constrained whenever one uses no detection threshold (i.e., C = 0 km s-1). This indicates that the detection threshold is not only useful to reject false detections due to intrinsic profile variability but is also a critical ingredient of the method. Interestingly, π is reasonably well constrained by the ΔHJD distribution alone, i.e. merit function (l), but a better overall result is obtained when used in conjunction with other diagnostic quantities.
The ΔRV and χ2 distributions are useful to refine the κ value but the uncertainties remain large. In essence, the ΔRV
and χ2 distributions carry similar information. Because merit functions using ΔRV tend to behave slightly better than those using χ2, and because the χ2 values are by definition much more sensitive to the exact knowledge of the measurement errors, we select our final merit function as given by the product of the PKS probabilities computed from the ΔHJD and ΔRV distributions and of the Binomial probability (Eq. (5)), hence merit function (u) in Table C.1.
Overall, the retrieved values of π and κ tend to be smaller than their input values but the correct indexes concur with the 1σ confidence intervals quoted in Table C.1. These confidence intervals can further be used to estimate the formal uncertainty of the method. Given that the best representation of the data are obtained with fbin = 0.51, π = −0.45 and κ = −1.00 (see Sect. 4.2), the bottom part of Table C.1 applies and we adopt σfbin = 0.04, σπ = 0.3 and σκ = 0.4.
Appendix D: Supplementary figures
 |
Fig. D.1
Ks-band magnitudes as a function of the spectral sub-types for luminosity classes V-IV (left panel), III (middle panel) and II-I (right panel). Different symbols identify the single stars, the low-amplitude RV variables and the binaries. Symbols for single and binaries of a given spectral-types have been shifted, compared to one another, by a small amount amount along the x-axis to improve the clarity of the plots. |
| Open with DEXTER | |
 |
Fig. D.2
Same as Fig. 11 for the luminosity classes V-IV (left panels), III (middle panels) and II-I (right panels). |
| Open with DEXTER | |
 |
Fig. D.3
Same as Fig. 12 for the luminosity classes V-IV (left panels), III (middle panels) and II-I (right panels). |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


