| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220239 | |
| Published online | 03 January 2013 | |
Online material
Appendix A: Synthetic spectrum of the integrated starlight
Spectral synthesis is a common method in investigations of stellar populations in external galaxies that are too distant to be resolved into individual stars. In this section we address the opposite problem: given the number densities and spatial distribution of the different types of stars in the solar neighbourhood, what is the spectrum of the integrated starlight (ISL) in different directions of sky and for different vantage points of an observer (or a globule) off the Galactic plane? In addition to the ISL, the Galactic surface brightness also contains the diffusely scattered starlight component, called the diffuse Galactic light (DGL). It contributes ca. 10–30% of the total light and has to be explicitly considered when estimating the total intensity of Galactic light. Because its spectrum is a copy of the ISL spectrum, it does not influence the strengths of the spectral features (absorption lines, bands, discontinuities), which are the main topic of our comparison of the ISL with the observed globule spectra. Our calculation of the ISL spectrum between 3000 and 10 000 Å follows the methods presented in Mattila (1980a,b). We here give a brief description of ISL spectral modelling appropriate for the comparison with the globule spectra. A more elaborate description and discussion of the results will be published in a separate paper.
A.1. Galaxy model
A simple model of the Galactic structure is adopted in which the stars and the dust
are distributed in plane-parallel layers. The stars are divided into representative
spectral groups and the number density of stars per pc3,
Di(z), and the
stellar emission coefficient per pc3,
ji(z), in each group
i are described by exponential density distributions in the
z-direction:  where
Di(0) and
ji(0) are the densities in the
galactic plane and hz,i the scale height.
The z-dependence of the extinction coefficient
a(z) (mag kpc-1) is approximated with
the formula
where
Di(0) and
ji(0) are the densities in the
galactic plane and hz,i the scale height.
The z-dependence of the extinction coefficient
a(z) (mag kpc-1) is approximated with
the formula  (A.3)where we adopted
a(0) = 1.75 mag/kpc (in V band) and
βd = 134 pc. The extinction coefficient
in the Galactic plane a(0) is the average value for the distance
range d = 0−2.5 kpc derived by Scheffler (1967a,b) from a
statistical analysis of the colour excesses of 4700 stars near the Galactic plane
(| z| < 75 pc) as provided by Neckel (1966). It agrees with the later estimates
of e.g. Hakkila et al. (1997) (≈ 1.5 mag/kpc)
and Mendez & van Altena (1998). The
scale height βd was adopted from Marshall et al. (2006) and is in accordance (within
~± 20 pc) with other determinations for the solar neighbourhood within a few kpc.
(A.3)where we adopted
a(0) = 1.75 mag/kpc (in V band) and
βd = 134 pc. The extinction coefficient
in the Galactic plane a(0) is the average value for the distance
range d = 0−2.5 kpc derived by Scheffler (1967a,b) from a
statistical analysis of the colour excesses of 4700 stars near the Galactic plane
(| z| < 75 pc) as provided by Neckel (1966). It agrees with the later estimates
of e.g. Hakkila et al. (1997) (≈ 1.5 mag/kpc)
and Mendez & van Altena (1998). The
scale height βd was adopted from Marshall et al. (2006) and is in accordance (within
~± 20 pc) with other determinations for the solar neighbourhood within a few kpc.
The results of Neckel (1966), which we used in our 1980 ISL modelling, have been derived for the more nearby Galactic environment, d ≤ 500 pc, and indicated an extinction coefficient a(0) = 2.46 mag kpc-1 (V) and a scale height corresponding to βd=40 pc. The ISL is, however, estimated to originate in a substantially higher volume around the Sun, reaching up to d ≥ 3 kpc in the Galactic plane.
For the wavelength dependence of interstellar extinction the formula given by Cardelli et al. (1989) for RV = 3.1 was adopted.
The clumpiness of the dust distribution has a profound effect on the ISL intensity.
For a given mean extinction coefficient the mean ISL intensity for the clumpy dust
distribution is higher than that for the homogeneous model. For a model consisting of
a uniform distribution of stars and dust clouds Chandrasekhar & Münch (1950) derived the following expression for
the mean ISL intensity: 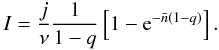 (A.4)Here
ν is the average number of clouds per kpc,
(A.4)Here
ν is the average number of clouds per kpc,
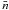 the mean number of clouds along the whole line of sight and q the
average transmissivity of a dust cloud
q = ⟨ exp(−τ) ⟩ , where τ is
the optical depth of one cloud. The parameters for the dust clumpiness correction were
adopted according to the two-component model of Scheffler (1967a,b): there are two
kinds of clouds with a mean optical thickness of
the mean number of clouds along the whole line of sight and q the
average transmissivity of a dust cloud
q = ⟨ exp(−τ) ⟩ , where τ is
the optical depth of one cloud. The parameters for the dust clumpiness correction were
adopted according to the two-component model of Scheffler (1967a,b): there are two
kinds of clouds with a mean optical thickness of
 and
and 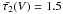 and a relative fequency of ν1 = 0.9 and
ν2 = 0.1.
and a relative fequency of ν1 = 0.9 and
ν2 = 0.1.
The numerical integration along each line of sight was performed in steps of 10 pc and extended to zmax = 3600 pc, which is well outside the dust distribution layer in the directions |b| ≠ 0. For distances z ≥ 3600 pc the ISL contribution was estimated and found to be negligible. For b = 0 deg the maximun distance along the plane was set to 10 kpc because high foreground extinction (17.5 mag at z = 0, 8.3 mag at z = 100) prevents any significant starlight to penetrate from beyond this distance. For directions close to the Galactic plane, b ≤ 10 deg, the maximum distance to which the numerical integration was extended from the plane was limited to zmax < 3600 pc by the condition not to exceed the maximun distance of 10 kpc along the plane. For details of the model and the other formulae used see Mattila (1980a).
A.2. Stellar distribution parameters Galaxy model
The division of stars into representative spectral groups covering the different parts of the HR-diagram was made according to the approach of Flynn et al. (2006) based on the analysis of the Hipparcos data base. Chris Flynn and Laura Portinari kindly provided us with their results in detailed tabular form. In these tables the stars are divided into the the following seven categories: (i, ii) main sequence (thin and thick disk); (iii, iv) clump stars (thin and thick disk); (v, vi) old giants (thin and thick disk); and (vii) young giants. For each category the tables give as a function of MV the stellar number density in the Galactic plane, D(0), and the scale height hz for a distribution of the form D(z) = D(0)sech(z/hz). In addition, the colour indices B − V and V − Ic based on the Hipparcos and Tycho catalogues were derived for each magnitude slot of the seven categories. Because of the limited distance range of Hipparcos, its coverage for the supergiants was sparse. We complemented this part by using the compilation of Wainscoat et al. (1992). Our adopted parameters for the stellar distributions are shown in Table A.1.
A.3. Stellar spectral library Galaxy model
For the comparison with the 3500−9000 Å scattered light spectra of the globules we need a spectral library with good spectral type and wide wavelength coverage but with only a relatively modest spectral resolution. The classical Pickles (1998) library fulfils these conditions best. In order to choose the best template stars from the library for each of our stellar slots as given in Table A.1 we used both the absolute magnitudes MV and the colour indices B − V and V − Ic as selection criteria. In most cases a satisfactory match with a Pickles template spectrum was possible. In a few cases we adopted the average of two nearby spectral templates. The Pickles catalogue numbers and spectral types for the chosen stellar templates are given in Table A.1.
A.4. Results Galaxy model
We show in Fig. A.1 the resulting ISL spectra for several galactic latitudes from |b| = 0 to 90 deg for an observer located in the plane (z = 0 pc). In Fig. A.1 we also show ISL spectra for z = 50 pc, corresponding to the estimated distance of the two globules. The two spectra at b = 11.5 and 23.8 deg are bracketing the latitude range of the two globules, b = −14.2 deg for
DC 303 and b = −15.9 deg for the TPN. We also show the mean spectrum over the whole sky for the two z values. It can be seen that the absorption lines, bands, and discontinuities are very similar in all these ISL spectra. The ISL intensity for intermediate and high positive Galactic latitudes decreases, as expected, when the observer moves to z = 50 pc. On the opposite side of the sky (b < 0), not shown in the figure, the ISL intensity increases correspondingly. The ISL intensity at Galactic equator increases, because the extinction coefficient at z = 50 pc is only 69% of its value at z = 0. The mean ISL intensity is seen to decrease modestly between z = 0 and z = 50 pc.
 |
Fig. A.1
Integrated starlight spectra for different Galactic latitudes and for two positions of the observer, z = 0 and z = 50 pc. The upper panels show the wavelength range 3500–10 000 Å, the lower panels show the wavelength range 3500–5500 Å. For z = 0 pc the spectra are shown from bottom to top for b = 90,36.8,11.5, and 0 deg as a black line. For z = 50 pc the spectra are shown from bottom to top for b = 90,36.8,23.6,11.5,5.7, and 0 deg as a black line. The mean spectra over the sky are shown as a red line. All spectra have the same scale and zero point. |
| Open with DEXTER | |
Data for stellar distribution parameters.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


