| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 18 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201220215 | |
| Published online | 29 November 2012 | |
Online material
Appendix A: Error analysis
 |
Fig. A1a
Temperature error map in orthographic projection at four different rotational phases. The maximum rms value is 80 K and the mean rms value is 50 K. Regions below a latitude of –30° are set to a constant value and do not participate in the error estimation. |
| Open with DEXTER | |
 |
Fig. A1b
Radial magnetic field error map in orthographic projection at four rotational phases, the maximum rms value is 125 G and the mean rms value is 64 G. |
| Open with DEXTER | |
In this section, we want to investigate the significance of our reconstruction results, in particular we want to quantify how sensitive the solution of the inverse problem is with respect to the initial conditions. In our DI and ZDI setup we deal with four parameter spaces (temperature, radial magnetic field, azimuthal magnetic field and meridional magnetic field) each of which with a dimension equal to the number of surface segments. The inversion algorithm has to navigate through the combined parameter spaces to find a solution that is compatible with the data. To study the stability of the inversion relative to the initial starting conditions (different positions in the parameter spaces) we use a simulation that runs the inversion with the original data set but from randomly chosen starting positions. Each parameter space is independently initialized by choosing a random value for each surface segment. Though we may create a considerable spread among the individual surface segments we can only consider a small fraction of the overall parameter space. Any exhaustive study to sample the parameter space is way out of reach for this high-dimensional setting and it is not the purpose here, instead we want to gain a quantitative measure how the result varies when the initial conditions are changed.
 |
Fig. A1c
Meridional magnetic field error in orthographic projection, the maximum rms value here is 101 G and the mean rms value is 51 G. |
| Open with DEXTER | |
 |
Fig. A1d
Azimuthal magnetic field error in orthographic projection with a maximum rms value of 106 G and a mean value of 52 G. |
| Open with DEXTER | |
A random generator on the basis of a normal distribution provides the values for each parameter space and surface segment. The underlying normal distribution has a mean value which is set to the effective temperature for the temperature component and to zero Gauss for all three magnetic components. The standard deviation is 250 K for the temperature and 250 G for all the magnetic components to provide a large spread among the individual surface segment values. The simulation (inversion with different initializations for all parameters and segments) is runfor 100 times on the original data set. For the so obtained 100 DI and ZDI maps we calculated the root-mean-square (rms) error to finally get rms error maps for each parameter. The individual inversions are all run to the same accuracy level given by the noise of the reconstructed data. Since the derivatives with respect to the magnetic parameters as well as with respect to the temperature become to weak below a latitude of –30 degrees to provide any substantial changes during the inversion we fix these segment values to zero for the magnetic maps and to the effective temperature for the temperature maps.
The rms error map for the temperature is shown in the orthographic plot Fig. A1a. It shows a peak value of 80 K at positions associated with the coolest regions (polar spot). Other regions hardly exceed a rms error of 50 K. The rms error map for the three magnetic components is shown in Figs. A1b, A1c, and A1d. The error map of the radial magnetic field has a peak value of 125 G, the average rms error value is 64 G. The rms error values for the meridional and azimuthal field exhibit peak values of 101 G and 106 G respectively and both have a mean rms error value around 60 G. What can be seen from these maps is that the error values are correlated with the absolute field strength as well as with the temperature. This emphasizes once more the influence of the temperature on the magnetic field determination. For the given photospheric conditions of V410 Tau a temperature change of just 80 K in a spot like region causes a change in the amplitude of the Stokes V signal of 4%. In the strong field regime of the polar spot this difference in amplitude is equivalent to a magnetic field of 60 G! Given this temperature dependence, the noise level in the data as well as the fact the a random small scale magnetic field on the surface produces local Stokes V signals that effectively cancel each other out, the obtained uncertainties from the error simulation are surprisingly low and show that the inversion always settle in the proximity of the same (local) minimum and that the solution is robust against perturbations of the initial conditions.
Appendix B: Test inversion with a dynamo model
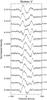 |
Fig. B.1
Stacked plot of the synthetic fits (dotted points) and the synthetic Stokes V profiles (grey solid lines) obtained from the dynamo model. |
| Open with DEXTER | |
 |
Fig. B2a
Orthographic maps of the original dynamo simulation which serves as a synthetic model for the test inversion, The model is shown at four different rotational phases φ. |
| Open with DEXTER | |
 |
Fig. B2b
Reconstructed surface field from 12 phase modulated Stokes V profiles. The number and order of the phases as well as the introduced noise correspond to the real observations of V410 Tau. Given the observational constraints imposed on this test inversion the dynamo model could be very well reproduced. |
| Open with DEXTER | |
In this section we want to examine if the inversion is able to retrieve a surface field topology as complicated as that of a simulated α2Ω-type dynamo with the given data set. The question that we want to investigate here goes beyond the testing of an inversion code with simplified surface topologies, what we want to do here is to seek a more direct answer to our problem, can we trust the hypothesis of our work that the reconstructed surface topology of V410 Tau is in fact similar to that of a given α2Ω-type dynamo simulation.
For that reason we synthesized from the α2Ω-dynamo simulation of Elstner & Korhonen (2005), 12 phase resolved spectra at phases which correspond to our observations. The dynamo model was scaled to have a peak field strength of 1920 G. The stellar parameter are those from V410 Tau given in Sect. 4.4. Noise is added according to the Bootstrap analysis in Sect. 3.2. The inversion with iMap is run with the same setup as the original inversion for V410 Tau, which also means that the inversion is stopped at the same noise level. Only Stokes V profiles are used for this magnetic inversion. The result is illustrated in the orthographic plots Figs. B2a and B2b as well as in the profile plot Fig. B.1. Given the number of available phases and the noise level in the data, the original magnetic field structure is remarkably good reproduced. Although the maximum field strength is not quite reached in the reconstruction shown in Fig. B2b one can see that the intertwined nature of the field structure and the rapid variation of the field lines around the polar region is well reproduced. The quality of the fit of the inversion relative to the original synthesized Stokes V profiles is shown in Fig. B.1. This demonstrates that with the given data set the inversion code can in fact reconstruct a surface field with a topology as complex as a α2Ω-type dynamo.
 |
Fig. C1
Reconstructed SVD profile originating from all 929 spectral lines (left). The reconstruction is performed with all eigenprofiles. The “quasi-noise” level introduced by the line blends has a median absolute deviation (MAD) of 1.56 × 10-5. On the right, reconstructed SVD profile with only one eigenprofile corresponding to the largest eigenvalue. The difference between the reconstruction using the full set of eigenprofiles is hardly visible and the rms between them is 2.22 × 10-5. |
| Open with DEXTER | |
Appendix C: The influence of line blends
Here we want to investigate how much information about the line blends may get lost within the rank estimation of the truncated SVD procedure. Note that in our analysis we compare the SVD reconstructed line profile with the synthetic (weighted) mean of all contributing lines (929 lines for Stokes V and 56 for Stokes I) where all significant line blends are accounted for. One might suspect that if information about the line blends is leaked into the noise subspace it may lead to a mismatch between the synthesized line profiles and the reconstructed profile which may cause problems in the subsequent inversion.
Let us concentrate on the Stokes V profiles here and have a look on how line blends influence the resulting profile from the two-stage SVD reconstruction. Line blends affect the individual lines used in the observation matrix in different ways, they occur at different positions within the line profiles, and are of different strength and number. So it will be of interest to see how much of the blends are finally recognized as systematic and correlated effects within the SVD reconstruction. For that purpose we have modeled a simple monopole star with a homogeneous magnetic field of 10 G and a small rotational velocity of 5 km s-1. All other stellar parameters are assumed to be the same as that for V410 Tau. We synthesize the line profiles in the velocity domain and use a value of ± 150 km s-1, around the respective line center of each contributing line. For such a small rotational velocity the Stokes V signals are therefore much thinner than the used velocity range. This wide span of the velocity domain will give us additional information about the systematics introduced by the line blends relative to the base level (i.e. zero polarized continuum). The 929 lines are calculated without any noise. After calculating the line profiles and their respective line blends we applied the SVD analysis and used all available eigenprofiles for the reconstruction. The result of the two stage process is an average Stokes V profile that is the same as a regular average since we have used the entire set of eigenprofiles. In Fig. C1 on the left side we see the result of the SVD reconstruction. It is clearly seen that the Stokes V profile has its regular shape in spite of the many contributing line blends. The wiggling is the result of the line blends. Note again no noise is present in that synthetic test case. This wiggling of the base line (the continuum) shows no dramatic variation within the velocity range. We may quantify this wiggling in terms of a noise measure, and use the median absolute deviation (MAD) for that purpose which is defined as, MAD(V) = median(| V1 − median(V)|,...,|Vn − median(V)|), where median(V) is the median of the vector components of V. The MAD give us a value of 1.56 × 10-5. Given the strength of the reconstructed Stokes V signal, which has an amplitude comparable to that observed for V410 Tau, we can see that the blends introduce an effect that is below the noise level of the real reconstructed observations. How much information is lost if we would just use the eigenprofile corresponding to the largest eigenvalue? In that case we would pretend that our signal subspace is of dimension one and all significant signal information is comprised
within the first eigenprofile. Performing the two-stage SVD reconstruction under this assumption results in a Stokes V profile shown on the right side in Fig. C1. The difference between the reconstruction with the full set of eigenvectors and that using only a single eigenprofile is very small. We calculated the rms between the two reconstructed profiles which gives a value of 2.22 × 10-5. The contribution of the line blends relative to the Stokes signal for the set of 929 spectral lines used in this work is apparently very small, i.e. ten times smaller than the noise level deduced in Sect. 3.2. The remaining systematic effects introduced by the blending are essentially captured by the first eigenprofile which is also the signal carrying component. This demonstrates that the influence of line blends for the set of spectral lines used in this work is small and that the leakage of information carried by eigenprofiles belonging to smaller eigenvalues (i.e. noise space) is negligible.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


