| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201220330 | |
| Published online | 07 November 2012 | |
Online material
Appendix A: Linewidth of recombination lines
RLs are broadened by several mechanisms: a natural broadening from the quantum uncertainty ΔE of the energy level E, a thermal/microturbulence Gaussian broadening from the motions of the emitting particles and of parcels of gas that are much smaller than the beam, the Stark (or “pressure”) broadening from the perturbation of the atomic energy levels by the electric field of neighboring charged particles, and a dynamical broadening from bulk flows (e.g., infall, rotation, outflow) in the gas. A detailed discussion of these processes and the physics of RLs can be found in Gordon & Sorochenko (2002).
For n > 20 (where Hnα is a n + 1 → n transition), the natural linewidth in velocity units is 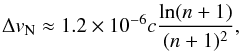 (A.1)where c is the speed of light. For H30α and H53α, ΔvN is 1.3 × 10-3 km s-1 and 0.5 × 10-3 km s-1, respectively. The natural broadening is negligible for radio and (sub)mm RLs.
(A.1)where c is the speed of light. For H30α and H53α, ΔvN is 1.3 × 10-3 km s-1 and 0.5 × 10-3 km s-1, respectively. The natural broadening is negligible for radio and (sub)mm RLs.
The thermal distributions of velocities of both the individual particles and small pockets of gas (“microturbulence”) produce a Gaussian contribution to the broadening. Neglecting microturbulence, the thermal FWHM is 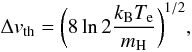 (A.2)where kB is the Boltzmann constant, mH is the hydrogen-atom mass, and it is assumed that all the gas is thermalized to the electron temperature Te. For a pure-hydrogen gas with Te = 9000 K, Δvth = 20.3 km s-1.
(A.2)where kB is the Boltzmann constant, mH is the hydrogen-atom mass, and it is assumed that all the gas is thermalized to the electron temperature Te. For a pure-hydrogen gas with Te = 9000 K, Δvth = 20.3 km s-1.
The pressure broadening has a Lorentzian shape, and it increases with density and quantum number. Collisions with ions and electrons make different contributions. The contribution from ions has the form (Gordon & Sorochenko 2002) 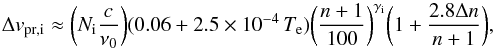 (A.3)where γi = 6−2.7 × 10-5 Te−0.13(n + 1)/100. For Te = 9000 K and Ni = 107 cm-3, the H30α line is virtually free from ion broadening (0.04 km s-1, and decreases close to linearly with decreasing Te), whereas the H53α line is broadened by 5.1 km s-1.
(A.3)where γi = 6−2.7 × 10-5 Te−0.13(n + 1)/100. For Te = 9000 K and Ni = 107 cm-3, the H30α line is virtually free from ion broadening (0.04 km s-1, and decreases close to linearly with decreasing Te), whereas the H53α line is broadened by 5.1 km s-1.
The collisions with electrons dominate the collisions with ions under most conditions. They produce a broadening of width (Smirnov et al. 1984): 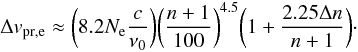 (A.4)For Ne = 107 cm-3, the electron broadenings for the H53α and H30α are ≈ 37.3 km s-1 and 0.6 km s-1, respectively.
(A.4)For Ne = 107 cm-3, the electron broadenings for the H53α and H30α are ≈ 37.3 km s-1 and 0.6 km s-1, respectively.
Finally, the last source of broadening is bulk motions (Δvdy) of the ionized gas, which may be in the form of outflows/winds, infall/accretion, and/or rotation. For unresolved observations, the method outlined here permits estimating the magnitude of these motions from the nonthermal linewidth of the line that is free of pressure broadening. Of course, ideally one wishes to spatially resolve these motions. ALMA in its Cycle 1 is now able to resolve the ionized-gas motions in sources as faint as ~10 mJy at the line peak at subarcsecond resolution.
Including all the contributions to the broadening, the total linewidth will have a Voigt profile with FWHM given by Eq. (1) in the text.
Appendix B: Cm and (sub)mm recombination lines
Here we discuss the advantages and limitations that cm and (sub)mm RLs have compared to each other. The cm lines are intrinsically fainter and optically thicker, and can be partially absorbed by the relatively high continuum opacity at their wavelengths (see e.g., Wilson et al. 2009). A possible drawback of (sub)mm RLs is that the free-free continuum may be contaminated by dust emission. Another problem is that they are out of LTE more easily than cm lines, so their interpretation may require careful modeling (e.g., Jiménez-Serra et al. 2011; Peters et al. 2012). As shown below, our simple LTE interpretation seems to be reasonable, but it is possible that a significant fraction of the 1.3-mm continuum comes from dust in the line of sight.
Let bn be the ratio of the population of level n to its LTE population. Then the actual line absorption coefficient κL is related to the LTE coefficient κL,LTE by (Gordon & Sorochenko 2002) 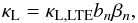 (B.1)with
(B.1)with 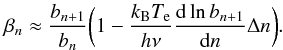 (B.2)While 0 < bn < 1 expresses the non-LTE level depopulation, βn can be negative when there are conditions for maser amplification.
(B.2)While 0 < bn < 1 expresses the non-LTE level depopulation, βn can be negative when there are conditions for maser amplification.
In the optically-thin case (τC,1.3mm ~ 0.08 from the data), the non-LTE corrected line intensity IL is (Gordon & Sorochenko 2002) 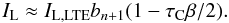 (B.3)Using the tabulated values in the calculations of Walmsley (1990), b30 ≈ 0.98 and β30 ~−1.5 for a density Ne = 107 cm-3. Therefore, the intensity of the H30α line is only amplified by ~3%. The H53α is even closer to LTE, with b53 ≈ 0.999 and β53 ~ 0.5.
(B.3)Using the tabulated values in the calculations of Walmsley (1990), b30 ≈ 0.98 and β30 ~−1.5 for a density Ne = 107 cm-3. Therefore, the intensity of the H30α line is only amplified by ~3%. The H53α is even closer to LTE, with b53 ≈ 0.999 and β53 ~ 0.5.
Sub(mm) RLs are more opticaly thin and intrinsically brighter than cm RLs. For a given Te and Ne, and in the Rayleigh-Jeans regime (hν ≪ kBTe), the line absorption coefficient decreases linearly with frequency κL ∝ ν-1, so the LTE line emission coefficient jL = κLBν(Te) ∝ ν. Similarly, the continuum absorption coefficient κC ∝ ν-2.1, so the LTE continuum emissivity jC ∝ ν-0.1. Therefore, in the optically thin regime, the line-to-continuum ratio increases almost linearly with frequency SLΔv/SC ∝ ν1.1. Under these assumptions, the expected ratio of the H30α to H53α line-to-continuum ratios is 6.4. However, the observed value is 1.6. If we assume that only ~32 mJy of the 1.3-mm continuum are due to free-free then the line-to-continuum ratio would increase to the expected value. This suggests that dust contributes a significant fraction to the (sub)mm continuum of BN. However, it is known (and we have confirmed this with the ALMA data set) that BN is not embedded in dense molecular gas. Therefore, it is unlikely that this line-of-sight dust arises in a dense core around BN.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


