| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201218887 | |
| Published online | 19 June 2012 | |
Online material
Appendix A: Velocity calibration
In order to obtain LOS velocities on an absolute scale, our Doppler shifts have to be calibrated to high precision and corrected for the systematic effects introduced by the Earth’s rotation, the orbital motion of Earth around the Sun, the solar rotation, as well as for the solar gravity redshift.
The final accuracy and precision have to be high enough to be able to measure typical photospheric Doppler shifts which, in the case of the Si i line, correspond to velocities in the range of few hundred m s-1. Since our spectral range comprises two telluric H2O lines, we can use these to calculate our sampling (Å per pixel). A Gaussian function with six terms was fit to the deepest part of these lines in our data in order to determine the position of their centers. The difference, Δx, is the distance between both lines in pixel units. The same process was carried out on the Fourier Transform Spectrometer (FTS) spectrum (Kurucz et al. 1984) from the Kitt Peak National Observatory, obtaining Δλ = 1.873 Å for the distance between both lines. The spectral sampling is merely calculated by dividing Δλ/Δx. This was done for each map using the average spectrum from a small non-magnetic region (containing about 1000 pixels). The mean spatial sampling of all maps is 11.035 ± 0.010 mÅ/px. Ideally, the sampling should always be the same. It can be theoretically calculated using the specifications of the telescope and of the spectrograph. A comparison with the theoretical sampling (11.240 mÅ/px) reveals that the calibration delivered a slightly smaller value, but not too different.
We are now able to construct the wavelength array using the calculated spectral sampling and a telluric line whose central wavelength is known, as a reference. According to the solar spectrum atlas of Swensson et al. (1970), the telluric line closest to the He i triplet has a wavelength of 10 832.120 Å, although the authors also provide another value: 10 832.150 Å. However, when we calculate the line center position using the Gaussian fit to the FTS spectrum we find a wavelength of 10 832.099 Å. Note that the wavelengths of the FTS atlas are not corrected for the gravity shift. This is perfectly adequate for telluric lines, which are, indeed, not affected by it. Other wavelength values, differing slightly from those mentioned previously, can also be found in the literature. These discrepancies led us to make our own estimate for the center wavelength of the H2O telluric line. The process, explained in Appendix B, results in a wavelength of 10 832.108 Å. This value is supported by the work of Breckinridge & Hall (1973), who inferred a wavelength of 10 832.109 Å with an accuracy approaching ± 1 mÅ.
The newly constructed wavelength array is referred to a terrestrial reference frame, that does not account for any relative orbital motions. We followed the calibration procedures presented in Appendix A of Martinez Pillet et al. (1997), and references therein, adapted to the Observatorio del Teide, to obtain absolute LOS velocities. Line shifts due to Earth’s rotation, orbital motion
of Earth around the Sun and solar rotation have been corrected. In the same way, the gravitational redshift, ΔλG = (GM⊙/R⊙c2)λ (which translates into 23 mÅ for this spectral range), was also corrected in our calibration. The effect of convective blueshift has been studied for the photospheric Si i line, however, after reviewing the literature and studying the response function to various physical perturbations of this line, we concluded that the correction is rather negligible owing to the formation height of the Si i line, which happens at a considerable height (log τ ~ −2) above the surface.
Appendix B: Determination of a new telluric line wavelength
As mentioned in the previous Appendix, the literature quotes several different values for the central wavelength (λT) of the H2O telluric line next to the He i triplet. We calibrated our spectrum using this telluric line as a reference, but the resulting velocity maps were clearly shifted to the red (when using λT = 10 832.120 Å) or to the blue (when using λT = 10 832.099 Å). This is, we found systematic photospheric redshifts or blueshifts (depending on the wavelength used for the calibration) in the faculae, where velocities are expected to be around zero (see Fig. 12 in Martinez Pillet et al. 1997, where high filling factor faculae show no velocity shift). Shifts on the same order of magnitude were found when compared to new data from a recent observing campaign in 2010 with the Tenerife Infrared Polarimeter at the VTT. We attribute this inconsistency to an incorrect value of the central wavelength of the telluric line and therefore we corrected its wavelength using the following method: we took three flat fields from our 2010 campaign with TIP-II (August 21 and 22); two from the morning and one from the afternoon. All of the flat fields were taken at disk center in the quiet sun, with a random circular movement of the telescope pointing of up to 50′′. These maps were then used as input data for the standard reduction procedure including flat field, dark current and polarimetric calibration corrections (Collados 1999, 2003). The spectral sampling for each flat field was inferred using the same procedure described in Appendix A. Using λT = 10 832.120 Å as the reference telluric line, a mean redshift of the Si i line of Δλ ~ 0.0117 Å was found. As mentioned above, this line is not expected to show any convective blueshift due to its formation height. Also no redshifts are expected at disk center. Thus, this systematic redshift was subtracted from the λT = 10 832.120 Å telluric line, yielding a new wavelength of 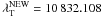 Å. With the new reference, the average photospheric facular velocity for all maps resulted in ~−0.06 km s-1. Since the faculae observed here are very compact and have large filling factors (typically, higher than 50%), this value is expected to be zero. We thus conclude that the systematic effects of our velocity calibration are smaller than 60 m s-1 or around 2 mÅ.
Å. With the new reference, the average photospheric facular velocity for all maps resulted in ~−0.06 km s-1. Since the faculae observed here are very compact and have large filling factors (typically, higher than 50%), this value is expected to be zero. We thus conclude that the systematic effects of our velocity calibration are smaller than 60 m s-1 or around 2 mÅ.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


