| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117623 | |
| Published online | 13 March 2012 | |
Online material
Appendix A: Aromatic cluster characterisation
In the study of polycyclic aromatic hydrocarbon (PAH) molecules and polycyclic aromatic clusters in hydrogenated amorphous carbon solids (a-C:H or HAC) we need to characterise the constituent aromatic structures in terms of their number of carbon atoms, nC, number of aromatic, six-fold rings, NR, or coordination number, m. It has been shown that NR is a function of the band gap, Eg, of a given hydrogenated amorphous carbon, i.e., NR = [5.8/Eg(eV)] 2, and that Eg can be expressed as a function of XH, i.e. Eg ~ 4.3XH, the aromatic coherence length, La(nm) = [0.77/Eg(eV)] , a measure of the aromatic domain size, also depends on the band gap (e.g., Robertson 1986, 1991).
In Sect. 2.2.1 we introduced an “aromatic cluster parameter”, Z, which is a function of NR and is simply the number of constraints, Ncon, per carbon atom for the given cluster, i.e., 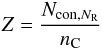 (A.1)where nC is the number of carbon atoms per aromatic cluster. For rather small and compact aromatic clusters such as pyrene, perylene, etc. Jones (1990) showed that
(A.1)where nC is the number of carbon atoms per aromatic cluster. For rather small and compact aromatic clusters such as pyrene, perylene, etc. Jones (1990) showed that 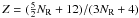 and for linear aromatic systems such as naphthalene and anthracene that Z = (5NR + 7)/(4NR + 2). For the linear clusters the expressions are valid for all NR. However, for compact clusters the expressions give a reasonable fit for NR ≤ 10 which is applicable to most of the aromatic clusters that occur in amorphous hydrocarbons (Robertson 1986) and therefore, by inference, in our eRCNs. Additionally, as pointed out by Robertson (1986), the compact clusters will be more stable that the row clusters.
and for linear aromatic systems such as naphthalene and anthracene that Z = (5NR + 7)/(4NR + 2). For the linear clusters the expressions are valid for all NR. However, for compact clusters the expressions give a reasonable fit for NR ≤ 10 which is applicable to most of the aromatic clusters that occur in amorphous hydrocarbons (Robertson 1986) and therefore, by inference, in our eRCNs. Additionally, as pointed out by Robertson (1986), the compact clusters will be more stable that the row clusters.
The relevant expressions for linear and compact aromatic clusters are shown in Table A.1. The compact cluster expression given in the upper part of the table is in fact that for bi-linear clusters, i.e., two parallel and connected linear structures. The middle part of the table gives the expressions for clusters consisting of a given number of rows of linear structures, Nrow, where in this case the values of NR are restricted to NR ≥ pNrow where p is an integer ≥ 1. The expressions for compact clusters that give reasonable fits for all NR are given in the lower part of the table.
Expressions for (polycyclic) aromatic cluster structures.
The expressions for the number of carbon atoms per aromatic cluster, nC, and the coordination number mcoord of the cluster are plotted in Fig. A.1. The dashed lines in this figure show the simple fits to the data for general aromatic clusters, which are valid for the most compact clusters containing up to about 10-rings but deviate for larger systems (the expressions for compact clusters are taken from the upper portion of Table A.1). The areas indicated by the vertical rows of dots show the values for all possible aromatic clusters with a given number of rings, i.e., the values for all possible isomers. The upper limits to the dots are for the most extended linear acenes (naphthalene, anthracene, tetracene, pentacene, etc.). Note that the simple expressions, represented by the dashed lines, give a very good representation of moderately compact clusters over the entire range of NR considered here.
 |
Fig. A.1
Number of carbon atoms nC (upper curves, diamonds) and coordination number mcoord (lower curves, triangles) for the most compact aromatic clusters possible (solid lines). The dashed lines show the simple fits to the data for general aromatic clusters. |
| Open with DEXTER | |
The coordination number per carbon atom in the aromatic cluster is plotted in Fig. A.2. In this figure the large diamonds show the values for the most compact aromatic clusters possible, i.e., for the large clusters these are the equivalent to the coronene, ovalene, circumcorenene, etc. structures. The small diamonds and their connecting dashed lines show the values for the multilinear acenes with Nrow = 1, 2, 3, 4 and 5 (from top to bottom). The small diamonds mark the actual cluster values and the dashed lines are calculated using the multilinear acene expressions (given in the middle of Table A.1). The horizontal dotted line indicates the limiting values (0.5) for simple linear acenes (Nrow = 1). Note that the compact cluster expression in the upper portion of Table A.1 is equivalent to the multilinear acene expression with Nrow = 2. The thick solid line gives a fit for the most compact aromatic clusters calculated using the expressions in the lower portion of Table A.1.
 |
Fig. A.2
Ratio of the coordination number m to the number of carbon atoms nC in aromatic clusters, i.e., the maximum possible number of peripheral aromatic cluster C–H bonds per carbon atom. See the text for a full description of the plotted data. |
| Open with DEXTER | |
Appendix B: eRCN model extension possibilities
The mathematical basis of the RCN and eRCN models (e.g., Phillips 1979; Döhler et al. 1980; Thorpe 1983; Angus & Jansen 1988; Jones 1990) is a pair of equations with three inter-dependent variables, viz., 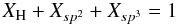 (B.1)and
(B.1)and 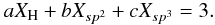 (B.2)Solutions to these equations are found by combining or “collapsing” two of the variables into a single one, i.e., Xsp3/Xsp2 ≡ R, and solving for R as a function of XH. It is therefore evident that the addition of any new structural component into the system introduces a new variable, which renders the resulting equations unsolvable because we then have two equations and four variables. This limitation could be circumvented in several ways:
(B.2)Solutions to these equations are found by combining or “collapsing” two of the variables into a single one, i.e., Xsp3/Xsp2 ≡ R, and solving for R as a function of XH. It is therefore evident that the addition of any new structural component into the system introduces a new variable, which renders the resulting equations unsolvable because we then have two equations and four variables. This limitation could be circumvented in several ways:
-
1.
By a collapsing of three of the variables into one, i.e.,Xsp/(Xsp3 + Xsp2) = P. However, this leads to ambiguities because of the degeneracy between the variables in the denominator and therefore to no useful or physically-realistic solutions.
-
2.
By fixing the concentration of the new component. This is a useful strategy but requires that the atomic fraction of the new component, W, is well-constrained by measurements and also that the number of involved atoms is invariant and independent of the network structure, i.e., no atomic loss, or transformation, of component W is allowed. New carbon atom hybridisation or polyatomic structures, such as sp1 C atoms or five-fold C5 aromatic rings, do not fulfil this condition and therefore cannot be treated in this way. The addition of hetero-atoms, such as O and N, should be possible using this approach, provided that their atomic abundances remain fixed. However, fixing the abundance of O and/or N atoms, and then treating their contribution as a constant, does not correctly take into account their accommodation into the structure and does not lead to realistic or useful solutions.
-
3.
By the elimination of one of the variables. For example, in order to introduce sp1 C atoms it is possible to eliminate either the Xsp3 or the Xsp2 component and then solve as a function of XH by combining the remaining two variables. However, in neither of these particular cases does this result in physically-meaningful solutions, which is not surprising since this treatment imposes unrealistic network constraints, i.e., networks consisting of only sp1 and sp2 atoms, with 2- and 3-fold coordination, or of only sp1 and sp3 atoms, with 2- and 4-fold coordination. The readers are left to verify this limitation for themselves.
In conclusion, it does not yet appear possible to add another carbon atom or hetero-atom component to the eRCN model in a physically-realistic way.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


